Lý luận - Số nhị phân được mã hóa
Số có cơ số 2 được gọi là số nhị phân. Số nhị phân được tạo bởi 0 và 1. Vì vậy, số nhị phân được mã hóa bao gồm hai quá trình. Một là chuyển đổi từ nhị phân sang thập phân và một là chuyển đổi từ thập phân sang nhị phân.
Số thập phân
Để biết cái gì binary numberlà, đầu tiên chúng ta phải biết về số thập phân. Vì vậy, số thập phân bao gồm mười chữ số (tức là 0,1,2,3,4,5,6,7,8,9). Bất kỳ hệ thập phân nào cũng có thể được biểu diễn bằng cách sử dụng các số này. Ví dụ, một dãy các chữ số là 2, 4, 6 và 8. Chúng ta thực hiện theo cách sau:
2468 = 2 × 10 3 + 4 × 10 2 + 6 × 10 1 + 8 × 10 0
= 2468
Note- Ta nhận giá trị của các số trong trường hợp này bằng cách nhân các chữ số khác nhau của dãy với lũy thừa của 10 và cộng. Ở đây 10 này được gọi là cơ số hoặc cơ số. Do đó dưới hệ thập phân, cơ số của chúng ta là 10.
Số nhị phân
Chúng tôi sử dụng mười chữ số để biểu thị một decimal number; như vậy chúng ta chỉ sử dụng hai chữ số để biểu diễn số nhị phân. Bất kỳ số nào cũng có thể được biểu diễn bằng cách sử dụng hai chữ số này, tức là 0 và 1.
Ví dụ về số nhị phân là- 1101. Ở đây có 4 chữ số trong dãy chữ số - 1, 1, 0, 1. Ta nhận giá trị theo cách sau.
1101 = 1 × 2 3 + 1 × 2 2 + 0 × 2 1 + 1 × 2 0
= 8 + 4 + 0 + 1 = 13
Do đó, số nhị phân đại diện cho mười ba trong hệ thập phân. Giá trị có thể được xác định bởimultiplying different digits của dãy bằng lũy thừa của 2 và cộng.
Conventional method - Trong ví dụ trên, chúng ta thấy rằng để lấy giá trị của một số nhị phân bất kỳ, chúng ta sử dụng quy tắc sau:
Chữ số đầu tiên từ bên phải được nhân với 2 0 = 1
Chữ số thứ hai từ bên phải được nhân với 2 1 = 2
Chữ số thứ ba từ bên phải được nhân với 2 2 = 4
Tương tự, chữ số thứ n từ bên phải được nhân với 2 n − 1
Cuối cùng, tất cả những thứ này được thêm vào.
For Example - Chuyển các số nhị phân sau thành số thập phân.
A - 1010
B - 1111
C - 100
D - 10000
Solution -
A - 1010 = 1 × 2 3 + 0 × 2 2 + 1 × 2 1 + 0 × 2 0
B - 1111 = 1 × 2 3 + 1 × 2 2 + 1 × 2 1 + 1 × 2 0
C - 100 = 1 × 2 2 + 0 × 2 1 + 0 × 2 0
D - 10000 = 1 × 2 4 + 0 × 2 3 + 0 × 2 2 + 0 × 2 1 + 0 × 2 0
Phương pháp nhanh hơn
Step I- Bắt đầu từ chữ số bên phải của số đã cho, viết 1, 2, 4, 8, 16, 32 ……. và tiếp tục như vậy bên dưới mỗi chữ số khi bạn tiến về phía bên trái.
Step II- Bỏ qua các số dưới 0s. Thêm tất cả các số dưới 1s.
Hãy giải ví dụ 1 bằng phương pháp này.
A - 1010
Chúng ta sẽ sử dụng 1,2,4,8 vì ở đây có 4 chữ số.
Chúng tôi nhận được,
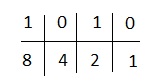
4 và 1 giảm xuống dưới số 0. Chúng tôi bỏ qua chúng và thêm phần còn lại. Chúng tôi nhận được 8 + 2 = 10
Như thế này chúng ta có thể giải các số khác.
Số thập phân có thể được chuyển đổi thành nhị phân bằng phương pháp successive divisions. Mỗi lần chia, cổ tức được chia cho 2. Lời nhắc được ghi nhận và thương số trở thành cổ tức tiếp theo, lại được chia cho 2. Quá trình này được lặp lại cho đến khi không thể chia được nữa.
Ví dụ - chuyển 17 thành số nhị phân -
Chia 17 cho 2 cho đến khi không chia được nữa.
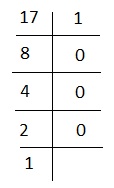
Vì vậy, dạng nhị phân của 17 là 10001.
Direction (Q. 1-4) − Study the following question and give the answer.
Trong một mã nhất định, ký hiệu cho 0 là + và cho 1 là #. Không có số hoặc biểu tượng nào lớn hơn 1. Giá trị của biểu tượng cho 1 tự nhân đôi mỗi khi nó dịch chuyển sang trái một chỗ.
'0' được mô tả là +
'1' được mô tả là #
'2' được mô tả là # +
'3' được mô tả là ##
'4' được mô tả là # ++, v.v.
1 - Hình nào sau đây sẽ tượng trưng cho số 11?
Options -
A - # + ##
B - + ## +
C - ## ++
D - # + # ++
E - không ai trong số này
Answer - Lựa chọn A
Explanation - Để tương đương với 11, ta dùng cách chia liên tiếp cho 2.

Vì vậy, dạng nhị phân sẽ là 10111. Thay 1 và 0 bằng # và + ta sẽ được # + ##.
2 - Hình nào sau đây sẽ tượng trưng cho số 8?
Options -
A - ## ++
B - + ## +
C - ## ++
D - ++ ##
E - không ai trong số này
Answer - Lựa chọn E
Explanation - cho 8, chúng tôi có-
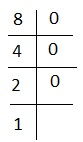
tức là 1000 hoặc # +++. Lựa chọn đúng là 5.
3 - Giá trị nào sau đây sẽ được biểu diễn bằng ## + #?
Options -
A - số 8
B - 11
C - 13
D - 12
E - không ai trong số này
Answer - Lựa chọn E
Explanation- ## + # = 1101 = 1 × 2 3 + 1 × 2 2 + 0 × 2 1 + 1 × 2 0 = 15
4 - Số nào sau đây sẽ được biểu diễn bằng # +++ #?
Options -
A - 22
B - 31
C - 14
D - 17
E - không ai trong số này
Answer - Lựa chọn D
Explanation - # + + + # = 10001
= 1 × 2 4 + 0 × 2 3 + 0 × 2 2 + 0 × 2 1 + 1 × 2 0
= 16 + 1 = 17
Hệ nhị phân có cơ số 2, hệ thập phân có cơ số 10 và hệ cấp ba có cơ số 3, trong khi hệ bát phân có cơ số 8. Trong trường hợp hệ cấp ba, chúng ta có ba chữ số để biểu diễn số. Đây là 0, 1 và 2. Trong trường hợp này, các số sẽ được chuyển thành số thập phân bằng cách nhân với lũy thừa 3 thích hợp.
For Example -
(12012) 3 = 1 × 3 4 + 2 × 3 3 + 0 × 3 2 + 1 × 3 1 + 2 × 3 0 = (104) 3