Khu vực hội tụ (ROC)
Khoảng biến thiên của σ mà biến đổi Laplace hội tụ được gọi là vùng hội tụ.
Các thuộc tính của ROC của Biến đổi Laplace
ROC chứa các đường dải song song với trục jω trong mặt phẳng s.

Nếu x (t) là tích phân tuyệt đối và nó có thời gian hữu hạn, thì ROC là toàn bộ mặt phẳng s.
Nếu x (t) là dãy vế phải thì ROC: Re {s}> σ o .
Nếu x (t) là dãy bên trái thì ROC: Re {s} <σ o .
Nếu x (t) là dãy hai cạnh thì ROC là tổ hợp của hai vùng.
ROC có thể được giải thích bằng cách sử dụng các ví dụ dưới đây:
Example 1: Find the Laplace transform and ROC of $x(t) = e-^{at}u(t)$
$ LT [x (t)] = LT [e - ^ {at} u (t)] = {1 \ over S + a} $
$ Re {} \ gt -a $
$ ROC: Re {s} \ gt> -a $

Example 2: Find the Laplace transform and ROC of $x(t) = e^{at}u(-t)$
$ LT [x (t)] = LT [e ^ {at} u (t)] = {1 \ over Sa} $
$ Re {s} <a $
$ ROC: Re {s} <a $

Example 3: Find the Laplace transform and ROC of $x(t) = e^{-at}u(t)+e^{at}u(-t)$
$ LT [x (t)] = LT [e ^ {- at} u (t) + e ^ {at} u (-t)] = {1 \ over S + a} + {1 \ over Sa} $
Với $ {1 \ over S + a} Re \ {s \} \ gt -a $
Với $ {1 \ over Sa} Re \ {s \} \ lt a $

Theo sơ đồ trên, vùng kết hợp nằm từ –a đến a. Vì thế,
$ ROC: -a <Re {s} <a $
Nhân quả và tính ổn định
Đối với một hệ thống là quan hệ nhân quả, tất cả các cực của hàm truyền của nó phải nằm bên phải một nửa mặt phẳng s.

Một hệ thống được cho là ổn định khi tất cả các cực của hàm truyền của nó nằm ở nửa bên trái của mặt phẳng s.

Một hệ được cho là không ổn định khi ít nhất một cực của hàm truyền của nó bị dịch chuyển sang nửa bên phải của mặt phẳng s.
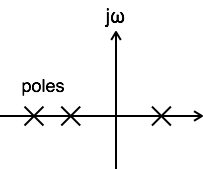
Một hệ được cho là ổn định biên khi có ít nhất một cực của hàm truyền của nó nằm trên trục jω của mặt phẳng s.

ROC của các chức năng cơ bản
| f (t) | F (s) | ROC |
|---|---|---|
| $ u (t) $ | $$ {1 \ over s} $$ | ROC: Re {s}> 0 |
| $ t \, u (t) $ | $$ {1 \ over s ^ 2} $$ | ROC: Re {s}> 0 |
| $ t ^ n \, u (t) $ | $$ {n! \ over s ^ {n + 1}} $$ | ROC: Re {s}> 0 |
| $ e ^ {at} \, u (t) $ | $$ {1 \ over sa} $$ | ROC: Re {s}> a |
| $ e ^ {- at} \, u (t) $ | $$ {1 \ over s + a} $$ | ROC: Re {s}> -a |
| $ e ^ {at} \, u (t) $ | $$ - {1 \ hơn sa} $$ | ROC: Re {s} <a |
| $ e ^ {- at} \, u (-t) $ | $$ - {1 \ over s + a} $$ | ROC: Re {s} <-a |
| $ t \, e ^ {at} \, u (t) $ | $$ {1 \ over (sa) ^ 2} $$ | ROC: Re {s}> a |
| $ t ^ {n} e ^ {at} \, u (t) $ | $$ {n! \ over (sa) ^ {n + 1}} $$ | ROC: Re {s}> a |
| $ t \, e ^ {- at} \, u (t) $ | $$ {1 \ over (s + a) ^ 2} $$ | ROC: Re {s}> -a |
| $ t ^ n \, e ^ {- at} \, u (t) $ | $$ {n! \ over (s + a) ^ {n + 1}} $$ | ROC: Re {s}> -a |
| $ t \, e ^ {at} \, u (-t) $ | $$ - {1 \ over (sa) ^ 2} $$ | ROC: Re {s} <a |
| $ t ^ n \, e ^ {at} \, u (-t) $ | $$ - {n! \ over (sa) ^ {n + 1}} $$ | ROC: Re {s} <a |
| $ t \, e ^ {- at} \, u (-t) $ | $$ - {1 \ over (s + a) ^ 2} $$ | ROC: Re {s} <-a |
| $ t ^ n \, e ^ {- at} \, u (-t) $ | $$ - {n! \ over (s + a) ^ {n + 1}} $$ | ROC: Re {s} <-a |
| $ e ^ {- at} \ cos \, bt $ | $$ {s + a \ over (s + a) ^ 2 + b ^ 2} $$ | |
| $ e ^ {- at} \ sin \, bt $ | $$ {b \ over (s + a) ^ 2 + b ^ 2} $$ |