Tín hiệu Các loại cơ bản
Dưới đây là một số tín hiệu cơ bản:
Chức năng bước đơn vị
Hàm bước đơn vị được ký hiệu là u (t). Nó được định nghĩa là u (t) = $ \ left \ {\ begin {matrix} 1 & t \ geqslant 0 \\ 0 & t <0 \ end {matrix} \ right. $

- Nó được sử dụng làm tín hiệu kiểm tra tốt nhất.
- Khu vực dưới chức năng bước đơn vị là thống nhất.
Chức năng xung đơn vị
Hàm xung được ký hiệu là δ (t). và nó được định nghĩa là δ (t) = $ \ left \ {\ begin {matrix} 1 & t = 0 \\ 0 & t \ neq 0 \ end {matrix} \ right. $

$$ \ int _ {- \ infty} ^ {\ infty} δ (t) dt = u (t) $$
$$ \ delta (t) = {du (t) \ over dt} $$
Tín hiệu đường dốc
Tín hiệu đường dốc được ký hiệu là r (t) và nó được định nghĩa là r (t) = $ \ left \ {\ begin {matrix} t & t \ geqslant 0 \\ 0 & t <0 \ end {matrix} \ right . $

$$ \ int u (t) = \ int 1 = t = r (t) $$
$$ u (t) = {dr (t) \ over dt} $$
Khu vực dưới đường nối đơn vị là thống nhất.
Tín hiệu Parabol
Tín hiệu parabol có thể được định nghĩa là x (t) = $ \ left \ {\ begin {matrix} t ^ 2/2 & t \ geqslant 0 \\ 0 & t <0 \ end {matrix} \ right. $
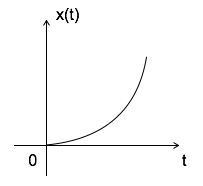
$$ \ iint u (t) dt = \ int r (t) dt = \ int t dt = {t ^ 2 \ over 2} = tín hiệu parabol $$
$$ \ Rightarrow u (t) = {d ^ 2x (t) \ over dt ^ 2} $$
$$ \ Rightarrow r (t) = {dx (t) \ over dt} $$
Hàm Signum
Hàm signum được ký hiệu là sgn (t). Nó được định nghĩa là sgn (t) = $ \ left \ {\ begin {matrix} 1 & t> 0 \\ 0 & t = 0 \\ -1 & t <0 \ end {matrix} \ right. $

Tín hiệu mũ
Tín hiệu hàm mũ có dạng x (t) = $ e ^ {\ alpha t} $.
Hình dạng của cấp số nhân có thể được xác định bởi $ \ alpha $.
Case i: nếu $ \ alpha $ = 0 $ \ đến $ x (t) = $ e ^ 0 $ = 1

Case ii:nếu $ \ alpha $ <0 tức là -ve thì x (t) = $ e ^ {- \ alpha t} $. Hình dạng được gọi là phân rã theo cấp số nhân.

Case iii:nếu $ \ alpha $> 0 tức là + ve thì x (t) = $ e ^ {\ alpha t} $. Hình dạng được gọi là nâng cao theo cấp số nhân.

Tín hiệu hình chữ nhật
Gọi nó được ký hiệu là x (t) và nó được định nghĩa là

Tín hiệu tam giác
Gọi nó được ký hiệu là x (t)

Tín hiệu hình sin
Tín hiệu hình sin có dạng x (t) = A cos ($ {w} _ {0} \, \ pm \ phi $) hoặc A sin ($ {w} _ {0} \, \ pm \ phi $ )
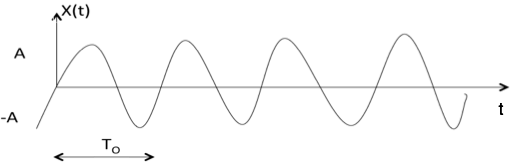
Trong đó T 0 = $ 2 \ pi \ over {w} _ {0} $
Hàm Sinc
Nó được ký hiệu là sinc (t) và nó được định nghĩa là sinc
$$ (t) = {sin \ pi t \ over \ pi t} $$
$$ = 0 \, \ text {for t} = \ pm 1, \ pm 2, \ pm 3 ... $$

Chức năng lấy mẫu
Nó được ký hiệu là sa (t) và nó được định nghĩa là
$$ sa (t) = {sin t \ over t} $$
$$ = 0 \, \, \ text {for t} = \ pm \ pi, \, \ pm 2 \ pi, \, \ pm 3 \ pi \, ... $$
