Kỹ thuật lấy mẫu tín hiệu
Có ba loại kỹ thuật lấy mẫu:
Lấy mẫu xung động.
Lấy mẫu tự nhiên.
Lấy mẫu phẳng Top.
Lấy mẫu xung
Lấy mẫu xung có thể được thực hiện bằng cách nhân tín hiệu đầu vào x (t) với tàu xung $ \ Sigma_ {n = - \ infty} ^ {\ infty} \ delta (t-nT) $ của chu kỳ 'T'. Ở đây, biên độ của xung thay đổi theo biên độ của tín hiệu đầu vào x (t). Đầu ra của bộ lấy mẫu được đưa ra bởi
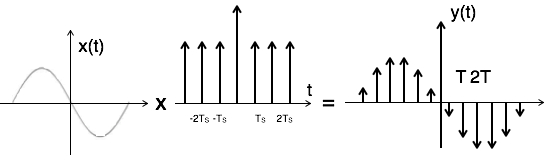
$ y (t) = x (t) × $ tàu xung lực
$ = x (t) × \ Sigma_ {n = - \ infty} ^ {\ infty} \ delta (t-nT) $
$ y (t) = y _ {\ delta} (t) = \ Sigma_ {n = - \ infty} ^ {\ infty} x (nt) \ delta (t-nT) \, ... \, ... 1 đô la
Để có được phổ của tín hiệu được lấy mẫu, hãy xem xét biến đổi Fourier của phương trình 1 ở cả hai phía
$ Y (\ omega) = {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} X (\ omega - n \ omega_s) $
Đây được gọi là lấy mẫu lý tưởng hoặc lấy mẫu xung. Bạn không thể sử dụng điều này thực tế bởi vì độ rộng xung không thể bằng 0 và việc tạo ra tàu xung là không thể thực tế.
Lấy mẫu tự nhiên
Lấy mẫu tự nhiên tương tự như lấy mẫu xung, ngoại trừ tập xung được thay thế bằng xung của chu kỳ T. tức là bạn nhân tín hiệu đầu vào x (t) với xung $ \ Sigma_ {n = - \ infty} ^ {\ infty} P ( t-nT) $ như hình bên dưới

Đầu ra của sampler là
$ y (t) = x (t) \ times \ text {tàu xung} $
$ = x (t) \ times p (t) $
$ = x (t) \ times \ Sigma_ {n = - \ infty} ^ {\ infty} P (t-nT) \, ... \, ... (1) $
Biểu diễn chuỗi Fourier theo cấp số nhân của p (t) có thể được cho dưới dạng
$ p (t) = \ Sigma_ {n = - \ infty} ^ {\ infty} F_n e ^ {jn \ omega_s t} \, ... \, ... (2) $
$ = \ Sigma_ {n = - \ infty} ^ {\ infty} F_n e ^ {j 2 \ pi nf_s t} $
Trong đó $ F_n = {1 \ over T} \ int _ {- T \ over 2} ^ {T \ over 2} p (t) e ^ {- jn \ omega_s t} dt $
$ = {1 \ trên TP} (n \ omega_s) $
Thay giá trị F n trong phương trình 2
$ \ do đó p (t) = \ Sigma_ {n = - \ infty} ^ {\ infty} {1 \ over T} P (n \ omega_s) e ^ {jn \ omega_s t} $
$ = {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} P (n \ omega_s) e ^ {jn \ omega_s t} $
Thay thế p (t) vào phương trình 1
$ y (t) = x (t) \ times p (t) $
$ = x (t) \ times {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} P (n \ omega_s) \, e ^ {jn \ omega_s t} $
$ y (t) = {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} P (n \ omega_s) \, x (t) \, e ^ {jn \ omega_s t} $
Để có được phổ của tín hiệu được lấy mẫu, hãy xem xét biến đổi Fourier trên cả hai phía.
$ FT \, [y (t)] = FT [{1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} P (n \ omega_s) \, x (t) \, e ^ { jn \ omega_s t}] $
$ = {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} P (n \ omega_s) \, FT \, [x (t) \, e ^ {jn \ omega_s t}] $
Theo tính chất dịch chuyển tần số
$ FT \, [x (t) \, e ^ {jn \ omega_s t}] = X [\ omega-n \ omega_s] $
$ \ do đó \, Y [\ omega] = {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} P (n \ omega_s) \, X [\ omega-n \ omega_s] $
Lấy mẫu phẳng trên cùng
Trong quá trình truyền, nhiễu được đưa vào ở đầu xung truyền, có thể dễ dàng loại bỏ nếu xung ở dạng đỉnh phẳng. Ở đây, đỉnh của các mẫu phẳng tức là chúng có biên độ không đổi. Do đó, nó được gọi là lấy mẫu đỉnh phẳng hoặc lấy mẫu thực tế. Lấy mẫu đầu phẳng tận dụng mạch mẫu và mạch giữ.

Về mặt lý thuyết, tín hiệu được lấy mẫu có thể thu được bằng tích chập của xung chữ nhật p (t) với tín hiệu được lấy mẫu lý tưởng là y δ (t) như thể hiện trong sơ đồ:
tức là $ y (t) = p (t) \ times y_ \ delta (t) \, ... \, ... (1) $

Để có được phổ được lấy mẫu, hãy xem xét biến đổi Fourier về cả hai phía cho phương trình 1
$ Y [\ omega] = FT \, [P (t) \ times y_ \ delta (t)] $
Bằng kiến thức về thuộc tính tích chập,
$ Y [\ omega] = P (\ omega) \, Y_ \ delta (\ omega) $
Đây $ P (\ omega) = T Sa ({\ omega T \ over 2}) = 2 \ sin \ omega T / \ omega $
Tỷ lệ Nyquist
Đây là tốc độ lấy mẫu tối thiểu mà tại đó tín hiệu có thể được chuyển đổi thành các mẫu và có thể được khôi phục trở lại mà không bị biến dạng.
Tốc độ Nyquist f N = 2f m hz
Khoảng thời gian Nyquist = $ {1 \ over fN} $ = $ {1 \ over 2fm} $ giây.
Lấy mẫu tín hiệu băng thông
Trong trường hợp tín hiệu vượt dải, phổ của tín hiệu vượt dải X [ω] = 0 đối với các tần số ngoài dải f 1 ≤ f ≤ f 2 . Tần số f 1 luôn lớn hơn 0. Ngoài ra, không có hiệu ứng răng cưa khi f s > 2f 2 . Nhưng nó có hai nhược điểm:
Tốc độ lấy mẫu có tỷ lệ lớn với f 2 . Điều này có những hạn chế thực tế.
Phổ tín hiệu được lấy mẫu có các khoảng trống phổ.
Để khắc phục điều này, định lý băng thông nói rằng tín hiệu đầu vào x (t) có thể được chuyển đổi thành các mẫu của nó và có thể được phục hồi trở lại mà không bị biến dạng khi tần số lấy mẫu f s <2f 2 .
Cũng thế,
$$ f_s = {1 \ over T} = {2f_2 \ hơn m} $$
Trong đó m là số nguyên lớn nhất <$ {f_2 \ over B} $
và B là băng thông của tín hiệu. Nếu f 2 = KB, thì
$$ f_s = {1 \ over T} = {2KB \ hơn m} $$
Đối với tín hiệu băng thông có băng thông 2f m và tốc độ lấy mẫu tối thiểu f s = 2 B = 4f m ,
phổ của tín hiệu lấy mẫu được cung cấp bởi $ Y [\ omega] = {1 \ over T} \ Sigma_ {n = - \ infty} ^ {\ infty} \, X [\ omega - 2nB] $