Cosmología - Guía rápida

Cosmologyes el estudio del universo. Rastreando en el tiempo, hubo varias escuelas de pensamientos sobre el origen del universo. Muchos eruditos creían en laSteady State Theory. Según esta teoría, el universo siempre fue el mismo, no tuvo comienzo.

Si bien había un grupo de personas que tenían fe en la Big Bang Theory. Esta teoría predice el comienzo del universo. Hubo evidencias de radiación caliente dejada fuera del Big Bang, lo que nuevamente apoya el modelo. La teoría del Big Bang predice la abundancia de elementos ligeros en el universo. Así, siguiendo el famoso modelo del Big Bang, podemos afirmar que el universo tuvo un comienzo. Vivimos en un universo en expansión.

El corrimiento al rojo del Hubble

A principios de 1900, el telescopio de última generación, Mt Wilson, un telescopio de 100 pulgadas, era el telescopio más grande entonces. Hubble fue uno de los científicos prominentes que trabajó con ese telescopio. Descubrió que había galaxias fuera de la Vía Láctea.Extragalactic Astronomytiene solo 100 años. Mt Wilson fue el telescopio más grande hasta que se construyó el Observatorio Palmer, que tenía un telescopio de 200 pulgadas.

HubbleNo era la única persona que observaba galaxias fuera de la Vía Láctea, Humason lo ayudó. Se propusieron medir los espectros de galaxias cercanas. Luego observaron que un espectro galáctico estaba en el rango de longitud de onda visible con emisión continua. Había líneas de emisión y absorción en la parte superior del continuo. A partir de estas líneas, podemos hacer una estimación de si la galaxia se está alejando de nosotros o hacia nosotros.

Cuando obtenemos un espectro, asumimos que la línea más fuerte proviene de H-α. De la literatura, la línea más fuerte debe ocurrir en6563 Å, pero si la línea ocurre en algún lugar alrededor 7000Å, podemos decir fácilmente que está desplazado al rojo.

Desde el Special Theory of Relativity,

$$ 1 + z = \ sqrt {\ frac {1+ \ frac {v} {c}} {1- \ frac {v} {c}}} $$

donde, Z es el corrimiento al rojo, un número adimensional yv es la velocidad de recesión.

$$ \ frac {\ lambda_ {obs}} {\ lambda_ {resto}} = 1 + z $$

Hubble y Humason enumerados 22 Galaxiesen su papel. Casi todas estas galaxias exhibieron corrimiento al rojo. Trazaron la velocidad (km / s) frente a la distancia (Mpc). Observaron una tendencia lineal y Hubble propuso su famosa ley de la siguiente manera.

$$ v_r = H_o d $$

Este es el Hubble Redshift Distance Relationship. El subíndicerindica que la expansión está en la dirección radial. Mientras que $ v_r $ es la velocidad de retroceso, $ H_o $ es el parámetro de Hubble,des la distancia de la galaxia a nosotros. Concluyeron que las galaxias lejanas se alejan más rápido de nosotros, si la tasa de expansión del universo es uniforme.

La expansión

Todo se aleja de nosotros. Las galaxias no son estacionarias, siempre hay alguna expansión armónica. Las unidades del parámetro de Hubble son km seg ⁻¹ Mpc ⁻¹ . Si uno recorre una distancia de -1 Mpc, las galaxias se moverían a una velocidad de 200 kms / seg. El parámetro de Hubble nos da la tasa de expansión. Según Hubble y Humason, el valor de $ H_o $ es 200 kms / seg / Mpc.

Los datos mostraron que todas las galaxias se están alejando de nosotros. Por tanto, es evidente que estamos en el centro del universo. Pero Hubble no cometió este error, según él, en cualquier galaxia en la que vivamos, encontraríamos a todas las demás galaxias alejándose de nosotros. Por tanto, la conclusión es que el espacio entre las galaxias se expande y no hay centro del universo.

La expansión está sucediendo en todas partes. Sin embargo, hay algunas fuerzas que se oponen a la expansión. Los enlaces químicos, la fuerza gravitacional y otras fuerzas atractivas mantienen unidos los objetos. Antes, todos los objetos estaban muy juntos. Considerando el Big Bang como una fuerza impulsiva, estos objetos están preparados para alejarse unos de otros.

Escala de tiempo

A escalas locales, la cinemática se rige por la gravedad. En la ley de Hubble original, había algunas galaxias que mostraban un desplazamiento al azul. Esto se puede atribuir al potencial gravitacional combinado de las galaxias. La gravedad ha desacoplado las cosas de la ley de Hubble. La Galaxia de Andrómeda viene hacia nosotros. La gravedad está intentando ralentizar las cosas. Inicialmente, la expansión se estaba desacelerando, ahora se está acelerando.

Hubo un Cosmic JerkDebido a esto. Se han realizado varias estimaciones del parámetro de Hubble. Ha evolucionado durante los 90 años de 500 kms / seg / Mpc a 69 kms / seg / Mpc. La disparidad en el valor se debió a la subestimación de la distancia. losCepheid Stars se utilizaron como calibradores de distancia, sin embargo existen diferentes tipos de estrellas Cefeidas y este hecho no se consideró para la estimación del parámetro de Hubble.

Hora del Hubble

La constante de Hubble nos da una estimación realista de la edad del universo. El $ H_o $ daría la edad del universo siempre que las galaxias se hayan estado moviendo con la misma velocidad. La inversa de $ H_o $ nos da el tiempo de Hubble.

$$ t_H = \ frac {1} {H_o} $$

Reemplazando el valor presente de $ H_o, t_H $ = 14mil millones de años. La tasa de expansión ha sido constante a lo largo del comienzo del Universo. Incluso si esto no es cierto, $ H_o $ da un límite útil sobre la edad del universo. Suponiendo una tasa de expansión constante, cuando trazamos una gráfica entre la distancia y el tiempo, la pendiente de la gráfica viene dada por la velocidad.

En este caso, el tiempo de Hubble es igual al tiempo real. Sin embargo, si el universo se había expandido más rápido en el pasado y más lento en el presente, el tiempo de Hubble da un límite superior de edad del universo. Si el universo se expandía lentamente antes y se aceleraba ahora, entonces el tiempo de Hubble dará un límite más bajo en la edad del universo.

• $ t_H = t_ {age} $ - si la tasa de expansión es constante.

• $ t_H> t_ {age} $ - si el universo se ha expandido más rápido en el pasado y más lento en el presente.

• $ t_H <t_ {age} $ - si el universo se ha expandido más lento en el pasado y más rápido en el presente.

Considere un grupo de 10 galaxias que se encuentran a 200 Mpc de otro grupo de galaxias. Las galaxias dentro de un cúmulo nunca concluyen que el universo se esté expandiendo porque la cinemática dentro de un grupo local está gobernada por la gravitación.

Puntos para recordar

• La cosmología es el estudio del pasado, presente y futuro de nuestro Universo.

• Nuestro universo tiene 14.000 millones de años.

• El universo se expande continuamente.

• El parámetro de Hubble es una medida de la edad del universo.

• Valor actual de H_o es de 69 kms / seg / Mpc.

Durante mucho tiempo, nadie consideró que las galaxias estuvieran presentes fuera de nuestra Vía Láctea. En 1924, Edwin Hubble detectóCepheid’sen la Nebulosa de Andrómeda y estimaron su distancia. Concluyó que estas "nebulosas espirales" eran de hecho otras galaxias y no una parte de nuestra Vía Láctea. Por lo tanto, estableció que M31 (Galaxia de Andrómeda) es un Universo Insular. Este fue el nacimiento deExtragalactic Astronomy.

El espectáculo de Cefeidas periodic dip in their brightness. Las observaciones muestran que el período entre caídas sucesivas llamado período de pulsaciones está relacionado con la luminosidad. Por tanto, pueden utilizarse como indicadores de distancia. Las estrellas de la secuencia principal como el Sol están en Equilibrio Hidrostático y queman hidrógeno en su núcleo. Una vez que el hidrógeno se quema por completo, las estrellas se mueven hacia la fase de Gigante Roja e intentan recuperar su equilibrio.

Las estrellas cefeidas son estrellas posteriores a la secuencia principal que están en tránsito desde las estrellas de la secuencia principal a las gigantes rojas.

Clasificación de las cefeidas

Hay 3 clases amplias de estas estrellas variables pulsantes:

• Type-I Cepheids (o Cefeidas clásicas) - período de 30 a 100 días.

• Type-II Cepheids (o W Virginis Stars) - período de 1 a 50 días.

• RR Lyrae Stars - período de 0,1-1 día.

En ese momento, Hubble no estaba al tanto de esta clasificación de estrellas variables. Es por eso que hubo una sobreestimación de la constante de Hubble, por lo que estimó una edad más baja de nuestro universo. Por lo tanto, también se sobrestimó la velocidad de la recesión. En Cefeidas, las perturbaciones se propagan radialmente hacia afuera desde el centro de la estrella hasta que se alcanza el nuevo equilibrio.

Relación entre brillo y período de pulsación

Intentemos ahora comprender la base física del hecho de que un período de pulsación más alto implica más brillo. Considere una estrella de luminosidad L y masa M.

Sabemos que

$$ L \ propto M ^ \ alpha $$

donde α = 3 a 4 para estrellas de baja masa.

Desde el Stefan Boltzmann Law, sabemos que -

$$ L \ propto R ^ 2 T ^ 4 $$

Si R es el radio y $ c_s $ es la velocidad del sonido, entonces el período de pulsación P se puede escribir como -

$$ P = R / c_s $$

Pero la velocidad del sonido a través de cualquier medio se puede expresar en términos de temperatura como:

$$ c_s = \ sqrt {\ frac {\ gamma P} {\ rho}} $$

Aquí, γ es 1 para casos isotérmicos.

Para un gas ideal, P = nkT, donde k es el Boltzmann Constant. Entonces, podemos escribir -

$$ P = \ frac {\ rho kT} {m} $$

donde $ \ rho $ es la densidad y m es la masa de un protón.

Por lo tanto, el período viene dado por:

$$ P \ cong \ frac {Rm ^ {\ frac {1} {2}}} {(kT) ^ {{\ frac {1} {2}}}} $$

Virial Theorem establece que para una distribución esférica estable, autogravitante de objetos de igual masa (como estrellas, galaxias), la energía cinética total k del objeto es igual a menos la mitad de la energía potencial gravitacional total u, es decir,

$$ u = -2k $$

Supongamos que el teorema del virial es válido para estas estrellas variables. Si consideramos un protón justo en la superficie de la estrella, a partir del teorema del virial podemos decir:

$$ \ frac {GMm} {R} = mv ^ 2 $$

De distribución de Maxwell,

$$ v = \ sqrt {\ frac {3kT} {2}} $$

Por lo tanto, punto -

$$ P \ sim \ frac {RR ^ {\ frac {1} {2}}} {(GM) ^ {\ frac {1} {2}}} $$

lo que implica

$$ P \ propto \ frac {R ^ {\ frac {3} {2}}} {M ^ {\ frac {1} {2}}} $$

Sabemos que - $ M \ propto L ^ {1 / \ alpha} $

También $ R \ propto L ^ {1/2} $

Entonces, para β > 0, finalmente obtenemos - $ P \ propto L ^ \ beta $

Puntos para recordar

• Las estrellas cefeidas son estrellas posteriores a la secuencia principal que están en tránsito desde las estrellas de la secuencia principal a las gigantes rojas.

• Las cefeidas son de 3 tipos: Tipo I, Tipo II, RR-Lyrae en orden decreciente de período pulsante.

• El período de pulsación de las cefeidas es directamente proporcional a su brillo (luminosidad).

Las observaciones de Hubble hicieron uso del hecho de que la velocidad radial está relacionada con el desplazamiento de la Spectral Lines. Aquí, observaremos cuatro casos y encontraremos una relación entre la velocidad de recesión ($ v_r $) y el desplazamiento al rojo (z).

Caso 1: Caso no relativista de origen en movimiento

En este caso, v es mucho menor que c. La fuente emite alguna señal (sonido, luz, etc.), que se propaga comoWavefronts. El intervalo de tiempo entre el envío de dos señales consecutivas en la trama fuente esΔts. El intervalo de tiempo entre la recepción de dos señales consecutivas en el marco del observador esΔto.

Si tanto el observador como la fuente están estacionarios, entonces Δts = Δto, pero este no es el caso aquí. En cambio, la relación es la siguiente.

$$ \ Delta t_o = \ Delta t_s + \ frac {\ Delta l} {c} $$

Ahora, $ \ Delta l = v \ Delta t_s $

Además, dado que (velocidad de onda x tiempo) = longitud de onda, obtenemos

$$ \ frac {\ Delta t_o} {\ Delta t_s} = \ frac {\ lambda_o} {\ lambda_s} $$

De las ecuaciones anteriores, obtenemos la siguiente relación:

$$ \ frac {\ lambda_o} {\ lambda_s} = 1 + \ frac {v} {c} $$

donde $ \ lambda _s $ es la longitud de onda de la señal en la fuente y $ \ lambda _o $ es la longitud de onda de la señal interpretada por el observador.

Aquí, dado que la fuente se aleja del observador, v es positivo.

Cambio rojo -

$$ z = \ frac {\ lambda_o - \ lambda_s} {\ lambda_s} = \ frac {\ lambda_o} {\ lambda_s} - 1 $$

De las ecuaciones anteriores, obtenemos el desplazamiento al rojo de la siguiente manera.

$$ z = \ frac {v} {c} $$

Caso 2: Caso no relativista de observador en movimiento

En este caso, v es mucho menor que c. Aquí, $ \ Delta l $ es diferente.

$$ \ Delta l = v \ Delta t_o $$

En la simplificación, obtenemos:

$$ \ frac {\ Delta t_o} {\ Delta t_s} = \ left (1 - \ frac {v} {c} \ right) ^ {- 1} $$

Obtenemos Red shift de la siguiente manera:

$$ z = \ frac {v / c} {1-v / c} $$

Ya que v << c, la expresión de desplazamiento al rojo para el Caso I y el Caso II es aproximadamente la misma.

Veamos en qué se diferencian los corrimientos al rojo obtenidos en los dos casos anteriores.

$$ z_ {II} - z_I = \ frac {v} {c} \ left [\ frac {1} {1 - v / c} -1 \ right] $$

Por tanto, $ z_ {II} - z_ {I} $ es un número muy pequeño debido al factor $ (v / c) ^ 2 $.

Esto implica que, si v << c, no podemos decir si la fuente se está moviendo o el observador se está moviendo.

Entendamos ahora el Basics of STR (Teoría especial de la relatividad) -

• La velocidad de la luz es constante.

• Cuando la fuente (u observador) se mueve con una velocidad comparable a la velocidad de la luz, se observan efectos relativistas.

• Dilatación del tiempo: $ \ Delta t_o = \ gamma \ Delta t_s $

• Contracción de longitud: $ \ Delta l_o = \ Delta t_s / \ gamma $

• Aquí, $ \ gamma $ es el Lorrentz factor, mayor que 1.

$$ \ gamma = \ frac {1} {\ sqrt {1- (v ^ 2 / c ^ 2)}} $$

Caso 3: Caso relativista de origen en movimiento

En este caso, v es comparable a c. Refiérase a la misma figura que en el Caso I. Debido al efecto relativista, se observa una dilatación del tiempo y por lo tanto se obtiene la siguiente relación. (La fuente se mueve con velocidad relativista)

$$ \ Delta t_o = \ gamma \ Delta t_s + \ frac {\ Delta l} {c} $$

$$ \ Delta l = \ frac {v \ gamma \ Delta t_s} {c} $$

$$ \ frac {\ Delta t_o} {\ Delta t_s} = \ frac {1 + v / c} {\ sqrt {1- (v ^ 2 / c ^ 2)}} $$

En una mayor simplificación, obtenemos,

$$ 1 + z = \ sqrt {\ frac {1 + v / c} {1-v / c}} $$

La expresión anterior se conoce como Kinematic Doppler Shift Expression.

Caso 4: Caso relativista de observador en movimiento

Consulte la misma figura que en el caso II. Debido al efecto relativista, se observa un acortamiento del tiempo y por lo tanto se obtiene la siguiente relación. (El observador se mueve con velocidad relativista)

$$ \ Delta t_o = \ frac {\ Delta t_s} {\ gamma} + \ frac {\ Delta l} {c} $$

$$ \ Delta l = \ frac {v \ Delta t_o} {c} $$

$$ \ frac {\ Delta t_o} {\ Delta t_s} = \ frac {\ sqrt {1- (v ^ 2 / c ^ 2)}} {1-v / c} $$

Con una mayor simplificación, obtenemos:

$$ 1 + z = \ sqrt {\ frac {1+ v / c} {1- v / c}} $$

La expresión anterior es la misma que obtuvimos para el Caso III.

Puntos para recordar

• La velocidad de recesión y el corrimiento al rojo de una estrella son cantidades relacionadas.

• En un caso no relativista, no podemos determinar si la fuente está en movimiento o estacionaria.

• En un caso relativista, no hay diferencia en la relación de desplazamiento al rojo-velocidad de recesión para la fuente o el observador en movimiento.

• Los relojes en movimiento se mueven más lento, es un resultado directo de la teoría de la relatividad.

Una galaxia que está en corrimiento al rojo z = 10, corresponde a v≈80% de c. La masa de la Vía Láctea está alrededor1011M⊙, si consideramos la materia oscura, es 1012M⊙. Nuestra vía láctea es, por tanto, masiva. Si se mueve al 80% dec, no encaja en el concepto general de cómo se mueven los objetos.

Sabemos,

$$ \ frac {v_r} {c} = \ frac {\ lambda_ {obs} - \ lambda {rest}} {\ lambda_ {rest}} $$

Para valores pequeños de z,

$$ z = \ frac {v_r} {c} = \ frac {\ lambda_ {obs} - \ lambda_ {rest}} {\ lambda_ {rest}} $$

En el siguiente gráfico, la clase entre flujo y longitud de onda, hay líneas de emisión en la parte superior del continuo. Desde elH-α información de línea, llegamos a la conclusión de que aproximadamente z = 7. Esto implica que la galaxia se mueve al 70% dec. Estamos observando un cambio y lo interpretamos como velocidad. Deberíamos deshacernos de esta noción y mirarzde una manera diferente. Imagina el espacio como una cuadrícula 2D que representa el universo como se muestra a continuación.

Considere la estrella negra como nuestra propia vía láctea y la estrella azul como alguna otra galaxia. Cuando registramos la luz de esta galaxia, vemos el espectro y descubrimos su corrimiento al rojo, es decir, la galaxia se está alejando. Cuando se emitió el fotón, tenía una velocidad relativa.

• ¿Y si el espacio se estuviera expandiendo?

• Es un corrimiento al rojo instantáneo del fotón. Los desplazamientos al rojo acumulativos a lo largo del espacio entre dos galaxias tenderán a producir un gran desplazamiento al rojo. La longitud de onda cambiará finalmente. Es la expansión del espacio más que el movimiento cinemático de las galaxias.

La siguiente imagen muestra si la gravedad mutua desborda la expansión, entonces esto no participa en la ley de Hubble.

En el desplazamiento Doppler cinemático, el desplazamiento al rojo se induce en un fotón en el momento de la emisión. En un corrimiento al rojo cosmológico, en cada paso, se produce un corrimiento al rojo acumulativo. En un potencial gravitacional, un fotón se desplazará al azul. A medida que sale del potencial gravitacional, se desplaza al rojo.

Según una teoría especial de la relatividad, dos objetos que pasan uno al lado del otro no pueden tener una velocidad relativa mayor que la velocidad de la luz. La velocidad de la que hablamos es la de la expansión del universo. Para valores grandes de z, el corrimiento al rojo es cosmológico y no una medida válida de la velocidad de recesión real del objeto con respecto a nosotros.

El principio cosmológico

Proviene del Copernicus Notiondel universo. Según esta noción, el universo es homogéneo e isotrópico. No hay una dirección y ubicación preferidas en el universo.

• La homogeneidad significa que no importa en qué parte del universo resida, verá que el universo es el mismo en todas las partes. La naturaleza isotrópica significa que no importa en qué dirección mire, verá la misma estructura.

• Un ejemplo apropiado de homogeneidad es un campo de arroz. Parece homogéneo en todas las partes, pero cuando el viento fluye, hay variaciones en su orientación, por lo que no es isotrópico. Considere una montaña en una tierra plana y un observador está parado en la cima de la montaña. Verá la naturaleza isotrópica del terreno llano, pero no es homogéneo. Si en un universo homogéneo, es isótropo en un punto, es isótropo en todas partes.

• Se han realizado estudios a gran escala para cartografiar el universo. Sloan Digital Sky Surveyes una de esas encuestas, que no se centró mucho en la declinación, sino en la ascensión recta. El tiempo de retroceso es de alrededor de 2 mil millones de años. Cada píxel corresponde a la ubicación de una galaxia y el color corresponde a la estructura morfológica. El color verde representa la galaxia espiral azul, mientras que el color rojo falso indica galaxias masivas.

• Las galaxias están allí en una estructura filamentosa en una red cosmológica y hay vacíos entre las galaxias.

• $ \ delta M / M \ cong 1 $ es decir, la fluctuación de la distribución de masa es 1 M es la masa de la materia presente dentro de un cubo dado. En este caso, tome el cubo de 50 Mpc de volumen.

• Para un lado del cubo de 1000 Mpc, $ \ delta M / M \ cong 10 ^ {- 4} $.

• Una forma de cuantificar la homogeneidad es tomar las fluctuaciones masivas. Las fluctuaciones de masa serán mayores en escalas más bajas.

• Para cuantificar la naturaleza isotrópica, considere la radiación de fondo de microondas cósmica. El universo es casi isotrópico a grandes escalas angulares.

Puntos para recordar

• Dos objetos que pasan uno junto al otro no pueden tener una velocidad relativa mayor que la velocidad de la luz.

• El principio cosmológico establece que el universo es homogéneo e isótropo.

• Esta homogeneidad existe a una escala angular muy grande y no a escalas menores.

• SDSS (Sloan Digital Sky Survey) es un esfuerzo para mapear el cielo nocturno, verificando el Principio Cosmológico.

Según la ley de conservación de la energía y la ley de conservación de la masa, la cantidad total de energía, incluida la masa (E = mc ² ), permanece sin cambios en cada paso de cualquier proceso del universo. La expansión del propio universo consume energía que tal vez provenga del estiramiento de la longitud de onda de los fotones (Desplazamiento al rojo cosmológico), Interacciones de energía oscura, etc.

Para acelerar el estudio de más de 26.000 galaxias, Stephen A. Shectmandiseñó un instrumento capaz de medir 112 galaxias simultáneamente. En una placa de metal se perforaron agujeros que correspondían a las posiciones de las galaxias en el cielo. Los cables de fibra óptica llevaron la luz de cada galaxia a un canal separado en un espectrógrafo en el telescopio du Pont de 2.5 metros en elCarnegie Observatories en Cerro Las Campanas en Chile.

Para una máxima eficiencia, una técnica especializada conocida como Drift-Scan Photometryse utilizó, en el que el telescopio se apuntó al comienzo de un campo de levantamiento y luego se apagó el accionamiento automático. El telescopio se detuvo mientras el cielo pasaba a la deriva. Las computadoras leen información delCCD Detectoral mismo ritmo que la rotación de la Tierra, produciendo una imagen larga y continua a una latitud celeste constante. Completar la fotometría tomó un total de 450 horas.

Existen diferentes formas de ruido y su modelado matemático es diferente dependiendo de sus propiedades. Varios procesos físicos hacen evolucionar el espectro de poder del universo a gran escala. El espectro de potencia inicial impartido debido a las fluctuaciones cuánticas sigue una tercera potencia de frecuencia negativa que es una forma dePink Noise Spectrum en tres dimensiones.

La métrica

En cosmología, primero se debe tener una definición de espacio. Una métrica es una expresión matemática que describe puntos en el espacio. La observación del cielo se realiza en geometría esférica; por tanto, se utilizará un sistema de coordenadas esféricas. La distancia entre dos puntos estrechamente espaciados viene dada por:

$$ ds ^ 2 = dr ^ 2 + r ^ 2 \ theta ^ 2 + r ^ 2 sin ^ 2 \ theta d \ phi ^ 2 $$

La siguiente imagen muestra la geometría en el espacio euclidiano no expansivo tridimensional.

Esta geometría todavía está en el espacio euclidiano tridimensional no expansivo. Por lo tanto, la cuadrícula de referencia que define el marco en sí se expandirá. La siguiente imagen muestra la métrica aumentada.

Se pone un factor de escala en la ecuación del espacio que no se expande, llamado 'factor de escala' que incorpora la expansión del universo con respecto al tiempo.

$$ ds ^ 2 = a ^ 2 (t) \ left [dr ^ 2 + r ^ 2 \ theta ^ 2 + r ^ 2 sin ^ 2 \ theta d \ phi ^ 2 \ right] $$

dónde a(t) es el factor de escala, a veces escrito como R(t). Mientras,a(t) > 1 significa aumento de la métrica, mientras que a(t) < 1 significa reducir la métrica y a(t) = 1significa métrica constante. Como convención,a(t₀) = 1.

Sistema de coordenadas comoving

en un Comoving Coordinate System, la escala de medición se expande junto con el marco (universo en expansión).

Aquí, $ \ left [dr ^ 2 + r ^ 2 \ theta ^ 2 + r ^ 2 sin ^ 2 \ theta d \ phi ^ 2 \ right] $ es la Distancia de Comoving, y $ ds ^ 2 $ es la Distancia adecuada.

La distancia adecuada corresponderá a la distancia real medida de una galaxia distante de la Tierra en el momento de la observación, también conocida como distancia instantánea de los objetos.

Esto se debe a que la distancia recorrida por un fotón cuando llega al observador desde una fuente distante será la recibida en $ t = t_0 $ del observador, lo que significaría que la distancia instantánea observada será la distancia adecuada, y se puede predecir distancias futuras utilizando el factor de velocidad y la longitud medida inicial como referencia.

El concepto de Comoving y la distancia adecuada es importante para medir el valor real de la densidad numérica de galaxias en el volumen dado del espacio observado. Se debe usar la distancia de Comoving para calcular la densidad en el momento de su formación cuando se emitió el fotón observado. Eso se puede obtener una vez que se pueda estimar la tasa de expansión del universo.

Para estimar la tasa de expansión, se puede observar el cambio en la distancia de una galaxia distante observada durante un largo período de tiempo.

Puntos para recordar

• Una métrica es una expresión matemática que describe los puntos en el espacio.

• El factor de escala determina si el universo se está contrayendo o expandiendo.

• En un sistema de coordenadas comoving, la escala de medición se expande junto con el marco (universo en expansión).

• La distancia adecuada es la distancia instantánea de los objetos.

• La distancia comoving es la distancia real de los objetos.

En este capítulo, comprenderemos en detalle la métrica de Robertson-Walker.

Modelo para factor de escala que cambia con el tiempo

Suponga que se emite un fotón desde una galaxia distante. El espacio está hacia adelante para fotones en todas las direcciones. La expansión del universo es en todas las direcciones. Veamos cómo cambia el factor de escala con el tiempo en los siguientes pasos.

Step 1 - Para un universo estático, el factor de escala es 1, es decir, el valor de la distancia comanditaria es la distancia entre los objetos.

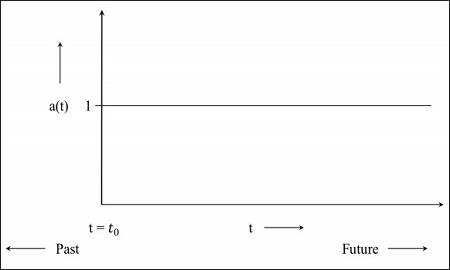
Step 2- La siguiente imagen es el gráfico del universo que aún se está expandiendo pero a un ritmo decreciente, lo que significa que el gráfico comenzará en el pasado. lost = 0 indica que el universo partió de ese punto.

Step 3 - La siguiente imagen es el gráfico del universo que se expande a un ritmo más rápido.

Step 4 - La siguiente imagen es el gráfico del universo que comienza a contraerse a partir de ahora.

Si el valor del factor de escala se vuelve 0 durante la contracción del universo, implica que la distancia entre los objetos se vuelve 0, es decir, la distancia adecuada se convierte 0. La distancia comoving, que es la distancia entre los objetos en un universo actual, es una cantidad constante. En el futuro, cuando el factor de escala se convierta en0, todo se acercará. El modelo depende del componente del universo.

La métrica para el universo plano en expansión (euclidiana: no hay un parámetro para la curvatura) se da como -

$$ ds ^ 2 = a ^ 2 (t) \ left (dr ^ 2 + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2 \ right) $$

Para el espacio-tiempo, el elemento de línea que obtuvimos en la ecuación anterior se modifica como -

$$ ds ^ 2 = c ^ 2dt ^ 2 - \ left \ {a ^ 2 (t) \ left (dr ^ 2 + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2 \ derecha) \ derecha \} $$

Para el espacio - tiempo, el momento en que se emite el fotón y cuando se detecta es diferente. La distancia adecuada es la distancia instantánea a los objetos que puede cambiar con el tiempo debido a la expansión del universo. Es la distancia que el fotón viajó desde diferentes objetos para llegar hasta nosotros. Se relaciona con la distancia comoviva como:

$$ d_p = a (t) \ times d_c $$

donde $ d_p $ es la distancia adecuada y $ d_c $ es la distancia comovolver, que es fija.

La distancia medida a los objetos en el universo presente se toma como la distancia comoviente, lo que significa que la distancia comoviente es fija y no cambia por la expansión. En el pasado, el factor de escala era menor que 1, lo que indica que la distancia adecuada era menor.

Podemos medir el corrimiento al rojo de una galaxia. Por lo tanto, la distancia adecuada $ d_p $ corresponde a $ c \ times t (z) $, donde $ t (z) $ es el tiempo de retroceso hacia un corrimiento al rojo yc es la velocidad de la luz en el vacío. El tiempo de retroceso es una función del corrimiento al rojo.(z).

Con base en la noción anterior, analicemos cómo se interpreta el desplazamiento cosmológico al rojo en este escenario de $ d_p = a (t) \ times d_c $.

Suponga que la galaxia, G. emite un fotón (que está ligado a la Tierra). El $ t_ {em} $ corresponde al momento en que se emitió el fotón; $ a (t_ {em}) $ era el factor de escala en el momento en que se emitió el fotón. En el momento de la detección del fotón, todo el universo se había expandido, es decir, el fotón está desplazado al rojo en el momento de la detección. El $ t_ {obs} $ corresponde al momento en que se detecta el fotón y el factor de escala correspondiente es $ a (t_ {obs}) $.

El factor por el cual ha crecido el universo viene dado por:

$$ \ frac {a (t_ {obs})} {a (t_ {em})} $$

El factor por el cual se ha expandido la longitud de onda es:

$$ \ frac {\ lambda_ {obs}} {\ lambda_ {em}} $$

que es igual al factor por el cual el universo ha crecido. Los símbolos tienen su significado habitual. Por lo tanto,

$$ \ frac {a (t_ {obs})} {a (t_ {em})} = \ frac {\ lambda_ {obs}} {\ lambda_ {em}} $$

Sabemos que el corrimiento al rojo (z) es -

$$ z = \ frac {\ lambda_ {obs} - \ lambda_ {em}} {\ lambda_ {em}} = \ frac {\ lambda_ {obs}} {\ lambda_ {em}} - 1 $$

$$ 1 + z = \ frac {a (t_ {obs})} {a (t_ {em})} $$

El valor actual del factor de escala es 1, por lo tanto $ a (t_ {obs}) = 1 $ y denota el factor de escala cuando el fotón fue emitido en el pasado por $ a (t) $.

Por lo tanto,

$$ 1 + z = \ frac {1} {a (t)} $$

Interpretación de Redshift en cosmología

Para entender esto, tomemos el siguiente ejemplo: Si $ z = 2 $ entonces $ a (t) = 1/3 $.

Implica que el universo se ha expandido en un factor de tres desde que la luz salió de ese objeto. La longitud de onda de la radiación recibida se ha expandido en un factor de tres porque el espacio se ha expandido en el mismo factor durante su tránsito desde el objeto emisor. Cabe señalar que a valores tan altos dez, el corrimiento al rojo es principalmente el corrimiento al rojo cosmológico, y no es una medida válida de la velocidad recesional real del objeto con respecto a nosotros.

Para el fondo cósmico de microondas (CMB), z = 1089, lo que significa que el universo actual se ha expandido en un factor de ∼1090. La métrica para el universo plano, euclidiano y en expansión se da como:

$$ ds ^ 2 = a ^ 2 (t) (dr ^ 2 + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2) $$

Deseamos escribir la métrica en cualquier curvatura.

Robertson and Walker probado para cualquier universo de curvatura (que es homogéneo e isotrópico), la métrica se da como -

$$ ds ^ 2 = a ^ 2 (t) \ left [\ frac {dr ^ 2} {1-kr ^ 2} + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2 \ right] $$

Esto se conoce generalmente como Robertson–Walker Metricy es cierto para cualquier topología del espacio. Tenga en cuenta el factor adicional en $ dr ^ 2 $. aquí es la constante de curvatura.

Geometría del universo

La geometría del universo se explica con la ayuda de las siguientes curvaturas, que incluyen:

• Curvatura positiva
• Curvatura negativa
• Curvatura cero

Entendamos cada uno de estos en detalle.

Curvatura positiva

Si un plano tangente dibujado en cualquier punto de la superficie de la curvatura no se cruza en ningún punto de la superficie, se llama superficie con una curvatura positiva, es decir, la superficie permanece en un lado del plano tangente en ese punto. La superficie de la esfera tiene curvatura positiva.

Curvatura negativa

Si un plano tangente dibujado en un punto de la superficie de la curvatura se cruza en cualquier punto de la superficie, se denomina superficie con una curvatura negativa, es decir, la superficie se curva alejándose del plano tangente en dos direcciones diferentes. Una superficie en forma de silla de montar tiene una curvatura negativa.

Ahora considere la superficie de una esfera. Si se construye un triángulo en la superficie de la esfera uniendo tres puntos con geodésico (arco de círculos máximos), la suma de los ángulos interiores del triángulo esférico es mayor que 180 ^o , es decir -

$$ \ alpha + \ beta + \ gamma> \ pi $$

Estos espacios se denominan espacios positivamente curvados. Además, la curvatura es homogénea e isotrópica. En general, el ángulo en los vértices del triángulo esférico sigue la relación:

$$ \ alpha + \ beta + \ gamma = \ pi + A / R ^ 2 $$

dónde A es el área del triángulo y Res el radio de la esfera. La siguiente imagen muestra un espacio curvado positivamente.

Para una curvatura positiva, las líneas paralelas deben encontrarse. Considere la superficie de la tierra, que es un espacio curvado positivamente. Tome dos puntos de partida en el ecuador. Las líneas que cruzan el ecuador en ángulo recto se conocen como líneas de longitud. Dado que estas líneas cruzan el ecuador en ángulos rectos, pueden denominarse líneas paralelas. Partiendo del ecuador, eventualmente se cruzan en los polos. Este método fue utilizado porCarl Gauss y otros para comprender la topología de la tierra.

Considere un espacio curvado negativamente (una silla que se muestra en la siguiente imagen), la suma de los ángulos interiores del triángulo es menos de 180 ^o , es decir,

$$ \ alpha + \ beta + \ gamma <\ pi $$

El ángulo en los vértices sigue la relación:

$$ \ alpha + \ beta + \ gamma = \ pi - A / R ^ 2 $$

Curvatura cero

Una superficie plana tiene curvatura cero. Ahora para un espacio plano, si se toma un plano y se construye un triángulo uniendo tres puntos con geodésicas (líneas rectas), la suma interior de ángulos será:

$$ \ alpha + \ beta + \ gamma = \ pi $$

La siguiente imagen es un espacio plano bidimensional.

Si se quiere que un espacio sea homogéneo e isotrópico, solo quedan tres posibilidades: el espacio puede ser uniformemente plano o puede tener una curvatura positiva uniforme o puede tener una curvatura negativa uniforme.

La constante de curvatura puede asumir cualquiera de los siguientes tres valores.

$$ k = \ begin {cases} +1, & para \: a \: positivamente \: curvado \: espacio; \\\ quad 0, & para \: a \: plano \: espacio; \\ - 1, & para \: a \: negativamente \: curvado \: espacio; \ end {casos} $$

Topología global del universo

El universo tiene una determinada topología, pero localmente puede tener arrugas. Dependiendo de cómo se distribuya la materia en el espacio, existen variaciones menores en la curvatura. Supongamos que hay una clase de objetos que tienen el mismo tamaño real sin importar en qué parte del universo se encuentren, lo que significa que son como velas estándar. No tienen el mismo brillo, pero tienen el mismo tamaño.

Si el objeto está en un espacio curvado positivamente y los fotones provienen del punto A (un extremo del objeto) y B (el otro extremo del objeto), los fotones se propagarán en paralelo en un espacio curvado positivamente a través de la trayectoria geodésica y finalmente se encontrarán . Para un observador en C, parecerá que provino de dos puntos diferentes en diferentes direcciones.

Si el objeto está en el universo local y medimos el tamaño angular, no se ve afectado por la curvatura. Si se ve la misma clase de objeto con un mayor corrimiento al rojo, el tamaño angular no se correlaciona con.

$$ \ theta = \ frac {d} {r} $$

Dónde d es el tamaño del objeto y res la distancia al objeto, es decir, si el tamaño es mayor que el tamaño local, significa que la curvatura es positiva. La siguiente imagen es una representación del fotón detectado en un espacio curvado positivamente.

Cabe señalar que no existe ningún objeto astrofísico real que sea de tamaño y morfología estándar. Aunque se pensaba que las galaxias cD elípticas masivas se ajustaban a las velas estándar, también se descubrió que evolucionaban con el tiempo.

Encontrar distancias a galaxias

En esta sección, discutiremos cómo encontrar la distancia a una galaxia teniendo en cuenta la siguiente imagen.

Considere la Vía Láctea en (r, θ,) en un marco de reposo cosmológico. Se puede tomar = 0; (0, θ, ϕ), es decir, el centro del universo invocando el supuesto de homogeneidad.

Considere una galaxia 'G' en (r1, θ,). La distancia (adecuada) es la distancia radial más corta recorrida por un fotón. De la simetría del espacio - tiempo, la geodésica nula de r = 0 a r = r1, tiene una dirección constante en el espacio. En su propagación radial, las coordenadas angulares no cambian. Si se cambian las coordenadas angulares, entonces no es el camino más corto. Esa es la razón por la que el término de curvatura está presente en dr ² .

Puntos para recordar

• La expansión del universo es en todas las direcciones.

• El universo puede ser estático, expandirse o contraerse según la evolución del factor de escala.

• Las galaxias CD evolucionan con el tiempo y, por lo tanto, no se pueden usar como velas estándar.

• El universo tiene cierta topología, pero localmente puede tener arrugas.

En este capítulo, analizaremos el parámetro de Hubble y el factor de escala.

• Prerequisite - Desplazamiento al rojo cosmológico, principios cosmológicos.

• Assumption - El universo es homogéneo e isotrópico.

Constante de Hubble con tasa fraccional de cambio de factor de escala

En esta sección, relacionaremos la constante de Hubble con la tasa fraccional de cambio de factor de escala.

Podemos escribir la velocidad de la siguiente manera y simplificar.

$$ v = \ frac {\ mathrm {d} r_p} {\ mathrm {d} t} $$

$$ = \ frac {d [a (t) r_c} {dt} $$

$$ v = \ frac {\ mathrm {d} a} {\ mathrm {d} t} \ ast \ frac {1} {a} \ ast (ar_c) $$

$$ v = \ frac {\ mathrm {d} a} {\ mathrm {d} t} \ ast \ frac {1} {a} \ ast r_p $$

Aquí, v es la velocidad de recesión, a es el factor de escala y r_p es la distancia adecuada entre las galaxias.

Hubble’s Empirical Formula era de la naturaleza -

$$ v = H \ ast r_p $$

Por lo tanto, comparando las dos ecuaciones anteriores obtenemos:

Hubble’s Parameter = Fractional rate of change of the scale factor

$$ H = da / dt \ ast 1 / a $$

Note- Esto no es una constante ya que el factor de escala es una función del tiempo. Por lo tanto, se llama parámetro de Hubble y no constante de Hubble.

Empíricamente escribimos:

$$ H = V / D $$

Por lo tanto, de esta ecuación, podemos inferir que dado que D está aumentando y V es una constante, entonces H se reduce con el tiempo y la expansión del universo.

Ecuación de Friedmann en conjunción con el modelo de Robertson-Walker

En esta sección, entenderemos cómo se usa la ecuación de Friedmann junto con el modelo de Robertson-Walker. Para entender esto, tomemos la siguiente imagen que tiene una masa de prueba a distanciar_p del cuerpo de masa M como ejemplo.

Teniendo en cuenta la imagen de arriba, podemos expresar la fuerza como:

$$ F = G \ ast M \ ast \ frac {m} {r ^ 2_p} $$

Aquí, G es la constante gravitacional universal y ρ es la densidad de materia dentro del universo observable.

Ahora, asumiendo una densidad de masa uniforme dentro de la esfera, podemos escribir:

$$ M = \ frac {4} {3} \ ast \ pi \ ast r_p ^ 3 \ ast \ rho $$

Usando estos en nuestra ecuación de fuerza obtenemos:

$$ F = \ frac {4} {3} \ ast \ pi \ ast G \ ast r_p \ ast \ rho \ ast m $$

Por tanto, podemos escribir la energía potencial y la energía cinética de la masa m como -

$$ V = - \ frac {4} {3} \ ast \ pi \ ast G \ ast r ^ 2_p \ ast m \ ast \ rho $$

$$ KE = \ frac {1} {2} \ ast m \ ast \ frac {\ mathrm {d} r_p ^ 2} {\ mathrm {d} t} $$

Utilizando el Virial Theorem -

$$ U = KE + V $$

$$ U = \ frac {1} {2} \ ast m \ ast \ left (\ frac {\ mathrm {d} r_p} {\ mathrm {d} t} \ right) ^ 2 - \ frac {4} { 3} \ ast \ pi \ ast G \ ast r_p ^ 2 \ ast m \ ast \ rho $$

Pero aquí, $ r_p = ar_c $. Entonces, obtenemos ...

$$ U = \ frac {1} {2} \ ast m \ ast \ left (\ frac {\ mathrm {d} a} {\ mathrm {d} t} \ right) ^ 2 r_c ^ 2 - \ frac { 4} {3} \ ast \ pi \ ast G \ ast r_p ^ 2 \ ast m \ ast \ rho $$

Con una mayor simplificación, obtenemos la ecuación de Friedmann,

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi} {3} \ ast G \ ast \ rho + \ frac {2U} {m} \ ast r_c ^ 2 \ ast a ^ 2 $$

aquí Ues una constante. También observamos que el universo en el que vivimos actualmente está dominado por la materia, mientras que la densidad de energía de radiación es muy baja.

Puntos para recordar

• El parámetro de Hubble se reduce con el tiempo y la expansión del universo.

• El universo en el que vivimos actualmente está dominado por la materia y la densidad de energía de radiación es muy baja.

En este capítulo, entenderemos qué es la ecuación de Friedmann y estudiaremos en detalle los modelos mundiales para diferentes constantes de curvatura.

Ecuación de Friedmann

Esta ecuación nos habla de la expansión del espacio en modelos homogéneos e isotrópicos del universo.

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho + \ frac {2U} {mr_c ^ 2a ^ 2} $ PS

Esto fue modificado en el contexto de General Relativity (GR) y Robertson-Walker Metric como sigue.

Usando ecuaciones GR -

$$ \ frac {2U} {mr_c ^ 2} = -kc ^ 2 $$

Dónde kes la constante de curvatura. Por lo tanto,

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho - \ frac {kc ^ 2} {a ^ 2} $ PS

Además, $ \ rho $ se reemplaza por densidad de energía que incluye materia, radiación y cualquier otra forma de energía. Pero para propósitos de representación, está escrito como $ \ rho $.

Modelos mundiales para diferentes constantes de curvatura

Veamos ahora las diversas posibilidades en función de los valores de la constante de curvatura.

Caso 1: k = 1, o universo cerrado

Para un universo en expansión, $ da / dt> 0 $. A medida que continúa la expansión, el primer término del lado derecho de la ecuación anterior es $ a ^ {- 3} $, mientras que el segundo término es $ a ^ {- 2} $. Cuando los dos términos se igualan, el universo detiene la expansión. Entonces ...

$$ \ frac {8 \ pi G} {3} \ rho = \ frac {kc ^ 2} {a ^ 2} $$

Aquí, k = 1, por lo tanto,

$$ a = \ left [\ frac {3c ^ 2} {8 \ pi G \ rho} \ right] ^ {\ frac {1} {2}} $$

Un universo así es finito y tiene un volumen finito. A esto se le llama Universo Cerrado.

Caso 2: k = -1, o universo abierto

Si k < 0, la expansión nunca se detendría. Después de algún tiempo, el primer término de la RHS puede despreciarse en comparación con el segundo término.

Aquí, k = -1. Por tanto, $ da / dt ∼ c $.

En este caso, el universo se está deslizando. Un universo así tiene un espacio y un tiempo infinitos. Esto se llama Universo Abierto.

Caso 3: k = 0, o universo plano

En este caso, el universo se expande a un ritmo decreciente. Aquí, k = 0. Por lo tanto,

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho $$

Un universo así tiene un espacio y un tiempo infinitos. A esto se le llama Universo Plano.

Puntos para recordar

• La ecuación de Friedmann nos habla de la expansión del espacio en modelos homogéneos e isotrópicos del universo.

• Dependiendo de los diferentes valores de las constantes de curvatura, podemos tener un Universo Cerrado, Abierto o Plano.

En este capítulo, discutiremos la ecuación de fluidos y cómo nos dice con respecto a la densidad del universo que cambia con el tiempo.

Estimación de ρ _cy ρ en el universo presente

Para el universo presente -

$$ \ rho_c \ simeq 10 ^ {11} M_ \ odot M_ {pc} ^ {- 3} \ simeq 10 \: hidrógeno \: átomos \: m ^ {- 3} $$

Existe una amplia gama de densidades críticas en nuestro espacio exterior. Por ejemplo, para el medio intergaláctico $ \ rho_c $ es 1 átomo de hidrógeno $ m ^ {- 3} $, mientras que para las nubes moleculares es $ 10 ^ 6 $ átomos de hidrógeno $ m ^ {- 3} $.

Debemos medir $ \ rho_c $ considerando muestras adecuadas de espacio. Dentro de nuestra galaxia, el valor de $ \ rho_c $ es muy alto, pero nuestra galaxia no es representativa de todo el universo. Entonces, deberíamos ir al espacio donde se cumple el principio cosmológico, es decir, distancias ≈ 300 Mpc. Mirar 300 Mpc significa mirar mil millones de años atrás, pero sigue siendo el universo actual.

Se realizan encuestas como SDSS para determinar la densidad de materia real. Toman un volumen de 5 × 500 × 5 Mpc ³ , cuentan el número de galaxias y suman toda la luz proveniente de estas galaxias. Bajo el supuesto de que 1 L ≡ 1 M, es decir, 1 Luminosidad solar ≡ 1 Masa solar.

Hacemos una conversión de luz a masa y luego intentamos estimar el número de bariones en función de las partículas de materia visible presentes en ese volumen.

Por ejemplo,

$$ 1000L_ \ odot ≡ 1000M_ \ odot / m_p $$

Donde, m _p = masa del protón.

Entonces obtenemos aproximadamente la densidad del número bariónico $ \ Omega b ∼ = 0.025 $. Esto implica $ \ rho b = 0.25% $ de $ \ rho_c $. Diferentes encuestas han arrojado un valor ligeramente diferente. Entonces, en el universo local, la densidad numérica de la materia visible es mucho menor que la densidad crítica, lo que significa que vivimos en un universo abierto.

La masa con un factor de 10 no se incluye en estos estudios porque estos estudios tienen en cuenta la radiación electromagnética pero no la materia oscura. Dando, $ \ Omega_m = 0.3 - 0.4 $. Aún así concluye que vivimos en un universo abierto.

La materia oscura interactúa con la gravedad. Mucha materia oscura puede detener la expansión. Aún no hemos formalizado cómo cambia $ \ rho $ con el tiempo, para lo cual necesitamos otro conjunto de ecuaciones.

La termodinámica establece que:

$$ dQ = dU + dW $$

Para un sistema que crece en términos de tamaño, $ dW = P dV $. La expansión del universo se modela como adiabática, es decir, $ dQ = 0 $. Por lo tanto, el cambio de volumen debería ocurrir por el cambio en la energía interna dU.

Tomemos un cierto volumen de universo de unidad como radio variable, es decir, $ r_c = 1 $. Si $ \ rho $ es la densidad del material dentro de este volumen de espacio, entonces,

$$ M = \ frac {4} {3} \ pi a ^ 3r_c ^ 3 \ rho $$

$$ U = \ frac {4} {3} \ pi a ^ 3 \ rho c ^ 2 $$

Dónde, Ues la densidad de energía. Descubramos el cambio en la energía interna con el tiempo a medida que el universo se expande.

$$ \ frac {\ mathrm {d} U} {\ mathrm {d} t} = 4 \ pi a ^ 2 \ rho c ^ 2 \ frac {\ mathrm {d} a} {\ mathrm {d} t} + \ frac {4} {3} \ pi a ^ 3 c ^ 2 \ frac {\ mathrm {d} \ rho} {\ mathrm {d} t} $$

De manera similar, el cambio de volumen con el tiempo viene dado por,

$$ \ frac {\ mathrm {d} V} {\ mathrm {d} t} = 4 \ pi a ^ 2 \ frac {\ mathrm {d} a} {\ mathrm {d} t} $$

Sustituyendo $ dU = −P dV $. Obtenemos,

$$ 4 \ pi a ^ 2 (c ^ 2 \ rho + P) \ dot {a} + \ frac {4} {3} \ pi a ^ 3c ^ 2 \ dot {\ rho} = 0 $$

$$ \ dot {\ rho} +3 \ frac {\ dot {a}} {a} \ left (\ rho + \ frac {P} {c ^ 2} \ right) = 0 $$

Esto se llama Fluid Equation. Nos dice cómo cambia la densidad del universo con el tiempo.

La presión cae a medida que el universo se expande. En cada instante la presión cambia, pero no hay diferencia de presión entre dos puntos en el volumen considerado, por lo que el gradiente de presión es cero. Solo los materiales relativistas imparten presión, la materia no tiene presión.

La Ecuación de Friedmann junto con la Ecuación de fluidos modela el universo.

Puntos para recordar

• La materia oscura interactúa con la gravedad. Mucha materia oscura puede detener la expansión.

• La ecuación fluida nos dice cómo cambia la densidad del universo con el tiempo.

• La Ecuación de Friedmann junto con la Ecuación de fluidos modela el universo.

• Solo los materiales relativistas imparten presión, la materia no tiene presión.

En este capítulo, discutiremos las soluciones a las ecuaciones de Friedmann relacionadas con el universo dominado por la materia. En cosmología, porque estamos viendo todo a gran escala, los sistemas solares, las galaxias, todo pasa a ser como partículas de polvo (eso es lo que lo vemos con nuestros ojos), podemos llamarlo universo polvoriento o universo solo materia.

En el Fluid Equation,

$$ \ dot {\ rho} = -3 \ left (\ frac {\ dot {a}} {a} \ right) \ rho -3 \ left (\ frac {\ dot {a}} {a} \ right ) \ left (\ frac {P} {c ^ 2} \ right) $$

Podemos ver que hay un término de presión. Por un universo polvorientoP = 0, porque la densidad de energía de la materia será mayor que la presión de radiación, y la materia no se mueve con velocidad relativista.

Entonces, la ecuación fluida se convertirá en,

$$ \ dot {\ rho} = -3 \ left (\ frac {\ dot {a}} {a} \ right) \ rho $$

$$ \ Flecha derecha \ dot {\ rho} a + 3 \ dot {a} \ rho = 0 $$

$$ \ Flecha derecha \ frac {1} {a ^ 3} \ frac {\ mathrm {d}} {\ mathrm {d} t} (a ^ 3 \ rho) = 0 $$

$$ \ Flecha derecha \ rho a ^ 3 = \: constante $$

$$ \ Flecha derecha \ rho \ propto \ frac {1} {a ^ 3} $$

No hay una intuición contraria en esta ecuación porque la densidad debe escalar como $ a ^ {- 3} $ porque el Volumen aumenta como $ a ^ 3 $.

De la última relación, podemos decir que,

$$ \ frac {\ rho (t)} {\ rho_0} = \ left [\ frac {a_0} {a (t)} \ right] ^ 3 $$

Para el universo presente, a, que es igual a a₀ debería ser 1. Entonces,

$$ \ rho (t) = \ frac {\ rho_0} {a ^ 3} $$

En un universo plano dominado por la materia, k = 0. Entonces, la ecuación de Friedmann se convertirá en,

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G \ rho} {3} $$

$$ \ dot {a} ^ 2 = \ frac {8 \ pi G \ rho a ^ 2} {3} $$

Al resolver esta ecuación, obtendremos,

$$ a \ propto t ^ {2/3} $$

$$ \ frac {a (t)} {a_0} = \ left (\ frac {t} {t_0} \ right) ^ {2/3} $$

$$ a (t) = \ left (\ frac {t} {t_0} \ right) ^ {2/3} $$

Esto significa que el universo seguirá aumentando a un ritmo decreciente. La siguiente imagen muestra la expansión de un universo polvoriento.

¿Cómo cambia ρ con el tiempo?

Eche un vistazo a la siguiente ecuación:

$$ \ frac {\ rho (t)} {\ rho_0} = \ left (\ frac {t_0} {t} \ right) ^ 2 $$

Sabemos que el factor de escala cambia con el tiempo como $ t ^ {2/3} $. Entonces,

$$ a (t) = \ left (\ frac {t} {t_0} \ right) ^ {2/3} $$

Diferenciándolo, obtendremos,

$$ \ frac {(da)} {dt} = \ dot {a} = \ frac {2} {3} \ left (\ frac {t ^ {- 1/3}} {t_0} \ right) $$

Sabemos que el Hubble Constant es,

$$ H (t) = \ frac {\ dot {a}} {a} = \ frac {2} {3t} $$

Esta es la ecuación para Einstein-de sitter Universe. Si queremos calcular la edad actual del universo, entonces,

$$ t_0 = t_ {edad} = \ frac {2} {3H_0} $$

Después de poner el valor de $ H_0 $ para el universo actual, obtendremos el valor de la edad del universo como 9 Gyrs. Hay muchosGlobular Cluster en nuestra propia galaxia, la Vía Láctea, que tienen edades más que eso.

Eso fue todo sobre el universo polvoriento. Ahora, si asume que el universo está dominado por la radiación y no por la materia, entonces la densidad de energía de la radiación es $ a ^ {- 4} $ en lugar de $ a ^ {- 3} $. Veremos más en el próximo capítulo.

Puntos para recordar

• En cosmología, todo resulta ser como partículas de polvo, por lo tanto, lo llamamos universo polvoriento o universo solo materia.

• Si asumimos que el universo está dominado por la radiación y no por la materia, entonces la densidad de energía de la radiación es $ a ^ {- 4} $ en lugar de $ a ^ {- 3} $.

En este capítulo, discutiremos las soluciones a las ecuaciones de Friedmann relacionadas con el universo dominado por radiación. Al principio, comparamos la densidad energética de la materia con la de la radiación. Esto nos permitirá ver si nuestro universo está dominado por la materia o por la radiación.

Densidad energética de la radiación

La radiación que prevalece en el universo actual se puede atribuir muy poco a las fuentes estelares, pero se debe principalmente al CMB remanente (Fondo de microondas cósmico).

La densidad de energía de la radiación, $ \ epsilon _ {\ gamma, 0} $, se puede expresar de la siguiente manera:

$$ \ epsilon _ {\ gamma, 0} = aT_0 ^ 4 $$

Aquí, a es la constante de radiación que tiene la expresión $ (8 \ pi ^ 5k_B ^ 4) / (15h ^ 3c ^ 2) $ igual a a = 7.5657 × 10⁻¹⁵erg\: cm⁻³ K⁻⁴. La Temperatura, T0, que consideramos aquí, corresponde a la del cuerpo negro correspondiente al CMB.

Sustituyendo los resultados, tenemos,

$$ \ epsilon _ {\ gamma, 0} = aT_0 ^ 4 = 4 \ times 10 ^ {- 13} erg \: cm ^ {- 3} $$

Densidad energética de la materia

En los siguientes cálculos, tenemos la suposición de trabajar con un universo plano y K = 0. Consideramos la densidad de energía de la materia como $ \ epsilon = \ rho c ^ 2 $. Consideramos lo siguiente:

$$ \ rho_ {m, 0} c ^ 2 = 0.3 \ rho_ {c, 0} c ^ 2 = 0.3 \ times \ frac {3H_0 ^ 2} {8 \ pi G} \ times c ^ 2 $$

$$ \ rho_ {m, 0} c ^ 2 \ simeq 2 \ times 10 ^ {- 8} erg \: cm ^ {- 3} $$

$$ \ rho_ {b, 0} c ^ 2 = 0.03 \ rho_ {c, 0} c ^ 2 = 0.03 \ times \ frac {3H_0 ^ 2} {8 \ pi G} \ times c ^ 2 $$

$$ \ rho_ {b, 0} c ^ 2 \ simeq 2 \ times 10 ^ {- 9} erg \: cm ^ {- 3} $$

Por lo tanto, del cálculo anterior, vemos que vivimos en un universo dominado por la materia. Esto puede apoyarse en el hecho de que el CMB está muy frío. Si miramos hacia atrás en el tiempo, la temperatura del CMB aumentaría y podríamos concluir que podría haber habido una época en la que el universo estuvo dominado por la radiación.

Variación de densidad y factor de escala

La ecuación del fluido nos muestra que:

$$ \ dot {\ rho} + 3 \ frac {\ dot {a}} {a} \ left (\ rho + \ frac {P} {c ^ 2} \ right) = 0 $$

Si consideramos un universo polvoriento, tendríamos P = 0. Dejando de lado los resultados anteriores, consideramos que el universo está dominado por la radiación.

$$ \ dot {\ rho} _ {rad} + 3 \ frac {\ dot {a}} {a} \ left (\ rho_ {rad} + \ frac {P} {c ^ 2} \ right) = 0 $$

Usando la relación de presión de $ P_ {rad} = \ rho c ^ {2/3} $ tenemos -

$$ \ dot {\ rho} _ {rad} + 3 \ frac {\ dot {a}} {a} \ left (\ rho_ {rad} + \ frac {\ rho_ {rad}} {3} \ right) = 0 $$

$$ \ dot {\ rho} _ {rad} + 4 \ frac {\ dot {a}} {a} (\ rho_ {rad}) = 0 $$

En una mayor simplificación, tenemos,

$$ \ frac {1} {a ^ 4} \ frac {\ mathrm {d}} {\ mathrm {d} t} (\ rho_ {rad} a ^ 4) = 0 $$

$$ \ rho_ {rad} a ^ 4 = \: constante $$

$$ \ rho_ {rad} \ propto \ frac {1} {a ^ 4} $$

El resultado anterior muestra un inversas 4 ^º variación de la potencia de un con $ \ rho $.

Esto se puede interpretar físicamente como $ a ^ {- 3} $ provenientes de la variación en el volumen a medida que aumenta. Los $ a ^ {- 1} $ restantes pueden tratarse como la energía perdida por el fotón debido a la expansión del espacio en el universo (corrimiento al rojo cosmológico 1 + z = a ^-1 ).

La siguiente imagen muestra la variación de la materia y la densidad de radiación con el tiempo.

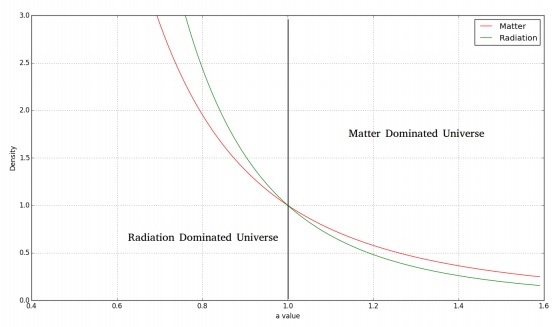
Para un universo plano dominado por la radiación, tendríamos la ecuación de Friedmann de la siguiente manera:

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G \ rho} {3} $$

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ frac {\ rho_0} {a ^ 4} $$

Al simplificar y aplicar la solución a la ecuación diferencial, tenemos:

$$ (\ dot {a}) ^ 2 = \ frac {8 \ pi G \ rho_0} {3a ^ 2} $$

$$ \ Flecha derecha a (t) \ propto t ^ {\ frac {1} {2}} $$

Por lo tanto, tenemos -

$$ a (t) = a_0 \ left (\ frac {t} {t_0} \ right) ^ {\ frac {1} {2}} $$

De la ecuación anterior, vemos que la tasa de aumento del factor de escala es menor que la del universo polvoriento.

Puntos para recordar

• La radiación que prevalece en el universo actual puede atribuirse muy poco a las fuentes estelares.

• Para un universo polvoriento, la presión es cero.

• CMB hace mucho frío.

El área de Energía Oscura es un área muy gris en astronomía porque es un parámetro libre en todas las ecuaciones, pero no hay una idea clara de qué es exactamente.

Empezaremos con las ecuaciones de Friedmann,

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho - \ frac {k \ ast c ^ 2} {a ^ 2} $$

La mayoría de los libros elementales sobre cosmología comienzan con la descripción de la energía oscura de este episodio de que antes de la observación de Hubble, el universo es cerrado y estático.

Ahora, para que el universo sea estático en el lado derecho, ambos términos deben coincidir y deben ser cero, pero si el primer término es mayor que el segundo término, entonces el universo no será estático, por lo que Einstein eliminó el parámetro libre. ∧ en la ecuación de campo para hacer que el universo esté estático, por lo que argumentó que no importa cuál sea el primer término en comparación con el segundo término, siempre se puede obtener un universo estático si hay un componente más en la ecuación, que puede compensar la dis- coincidencia entre estos dos términos.

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho - \ frac {k \ ast c ^ 2} {a ^ 2} + \ frac {\ wedge} {3} $$

$$ \ left (\ frac {\ ddot {a}} {a} \ right) = - \ frac {4 \ pi G} {3} \ left (\ rho + \ frac {3P} {c ^ 2} \ derecha) + \ frac {\ wedge} {3} $$

Donde $ P = \ rho \ ast c ^ 2/3 $ y $ \ wedge = \ rho \ ast c ^ 2 $ es el parámetro cosmológico. (El signo negativo es solo por atracción)

En la ecuación anterior (ecuación de aceleración):

• $ 3P / c ^ 2 $ es la presión negativa debida a la radiación,

• $ -4 \ pi G / 3 $ es la atracción debida a la gravedad, y

• $ \ wedge / 3 $ hace una contribución positiva.

El tercer término actúa como una fuerza repulsiva porque otra parte de la ecuación es atractiva.

El significado físico de la ecuación es que ˙a = 0porque no había ninguna evidencia que muestre que el universo se está expandiendo. ¿Qué pasa si estos dos términos no coinciden entre sí, entonces es mejor agregar un componente y dependiendo del desplazamiento siempre podemos cambiar el valor del parámetro libre?

En ese momento no existía una explicación física sobre estos parámetros cosmológicos, razón por la cual cuando se descubrió la explicación del universo en expansión en la década de 1920, donde Einstein inmediatamente tuve que descartar esta constante.

La explicación de esto cosmological constant todavía está en uso porque explica una versión diferente del universo, pero la definición de esta constante cosmológica, la forma de interpretación, fue cambiando con el tiempo.

Ahora bien, el concepto de esta constante cosmológica ha vuelto a la cosmología por muchas razones. Una de las razones es que tenemos observaciones de la densidad de energía de diferentes componentes del universo (bariónico, materia oscura, radiación), por lo que sabemos cuál es este parámetro. Observaciones independientes usandocosmic microwave background muestra que k = 0.

$$ CMB, k = 0 \: \ rho = \ rho_c = \ frac {3H_0 ^ 2} {8 \ pi G} \ approx 10 \: Hidrógeno \: átomos.m ^ {- 3} $$

Para que k sea 0, $ \ rho $ debería ser igual a $ \ rho_c $, pero todo lo que sabemos si lo sumamos no da 0, lo que significa que hay algún otro componente que muestra que es mucho menor que $ \ rho_c $.

$$ \ rho = \ rho_b + \ rho_ {DM} + \ rho_ {rad} << \ rho_c $$

Una evidencia más de la energía oscura proviene del Type 1 Supernova Observationque ocurre cuando la enana blanca acrecienta la materia y excede el límite de Chandrashekhar, que es un límite muy preciso (≈ 1.4M). Ahora, cada vez que ocurre una explosión de supernova tipo 1, tenemos la misma masa, lo que significa que la energía de enlace total del sistema es la misma y la cantidad de energía luminosa que podemos ver es la misma.

Por supuesto, la luz de la supernova aumenta y luego se desvanece, pero si mide el brillo máximo, siempre será el mismo, lo que lo convierte en un candidato estándar. Entonces, con una supernova de tipo 1 que usamos para medir el componente cosmológico del universo y los astrónomos encontraron que la supernova con un alto desplazamiento al rojo es 30% - 40% más débil que la supernova de bajo desplazamiento al rojo y se puede explicar si hay alguna -cero∧ término.

En modelos cosmológicos DE (Dark Energy)se trata como un fluido, lo que significa que podemos escribir la ecuación de estado para él. La ecuación de estado es la ecuación que conecta las variables como Presión, Densidad, Temperatura y Volumen de dos estados diferentes de la materia.

Dimensionalmente vemos,

$$ \ frac {8 \ pi G} {3} \ rho = \ frac {\ wedge} {3} $$

$$ \ rho_ \ wedge = \ frac {\ wedge} {8 \ pi G} $$

Densidad energética de DE,

$$ \ epsilon_ \ wedge = \ rho_ \ wedge \ ast c ^ 2 = \ frac {\ wedge c ^ 2} {8 \ pi G} $$

Parámetro de densidad de energía oscura,

$$ \ Omega_ \ wedge = \ frac {\ rho_ \ wedge} {\ rho_c} $$

$ \ Omega_ \ wedge $ es la densidad de la energía oscura en términos de densidad crítica.

$$ \ rho = \ rho_b + \ rho_ {DM} + \ rho_ \ wedge $$

Hay una serie de teorías sobre la energía oscura, que repele el universo y hace que el universo se expanda. Una hipótesis es que esta energía oscura podría ser una densidad de energía del vacío. Suponga que el espacio mismo está procesando algo de energía y cuando cuenta la cantidad de materia bariónica, materia oscura y la radiación dentro de la unidad de volumen de espacio, también está contando la cantidad de energía que está asociada con el espacio, pero no está claro que la energía oscura es realmente una densidad de energía del vacío.

Sabemos que la relación entre la densidad y el factor de escala para la materia oscura y la radiación son,

$$ \ rho_m \ propto \ frac {1} {a ^ 3} $$

$$ \ rho_m \ propto \ frac {1} {a ^ 4} $$

Tenemos la gráfica de factor de escala de densidad v / s. En la misma gráfica, podemos ver que $ \ rho_ \ wedge $ es una constante con la expansión del universo que no depende del factor de escala.

La siguiente imagen muestra la relación entre la densidad y el factor de escala.

‘ρ’ v/s ‘a’(factor de escala que está relacionado con el tiempo) en el mismo gráfico, la energía oscura se modela como una constante. Entonces, cualquier energía oscura que midamos en el universo actual, es una constante.

Puntos para recordar

• Las observaciones independientes que utilizan el fondo cósmico de microondas muestran que k = 0.

• $ \ rho_ \ wedge $ es una constante con la expansión del universo que no depende del factor de escala.

• La gravedad también está cambiando con el tiempo, lo que se llama modified Newtonian dynamics.

En este capítulo, analizaremos las curvas de rotación de las galaxias espirales y la evidencia de la materia oscura.

Materia oscura y hechos de observación sobre la materia oscura

• La primera evidencia de la materia oscura fue la study of the Kinematics of Spiral Galaxy.

• El Sol está desplazado a 30.000 años luz del centro de nuestra Galaxia. La velocidad céntrica galáctica es de 220 km / s.

• ¿Por qué la velocidad 220 km / s no es 100 km / so 500 km / s? ¿Qué gobierna el movimiento circular del objeto?

• La masa encerrada dentro del radio ayuda a detectar la velocidad en el Universo.

Rotación de la Vía Láctea o Galaxia Espiral - Rotación diferencial

• Angular Velocity varía con la distancia desde el centro.

• El período de tiempo orbital depende de la distancia desde el centro.

• El material más cercano al centro galáctico tiene un período de tiempo más corto y el material lejos del centro galáctico tiene un período de tiempo más largo.

Curva de rotacion

• Predecir el cambio de velocidad con el Galactic centric radius. La curva que da la velocidad cambia con el radio orbital.

• Cuando vemos que las cosas se mueven, pensamos que es la gravedad la que influye en la rotación.

• La distribución de masa varía con el radio. La densidad de la materia predecirá la curva de rotación. La curva de rotación basada en la densidad de la materia, que varía con el radio.

Brillo de superficie

• Elegimos el parche y vemos cuánta luz sale.

• La cantidad de luz que proviene del parche se denomina brillo de superficie.

• Su unidad es mag/arcsec².

• Si encontramos que el brillo de la superficie varía con el radio, podemos encontrar que la materia luminosa varía con el radio.

  $$ \ mu (r) \ propto exp \ left (\ frac {-r} {h_R} \ right) $$

  $ h_R $ es la longitud de la escala. $ \ mu (r) = \ mu_o \ ast exp \ left (\ frac {-r} {h_R} \ right) $

• $ h_R $ es casi 3 kpc para la Vía Láctea.

Galaxias espirales

Para que los astrónomos entiendan la curva de rotación, dividieron las galaxias en dos componentes, que son:

• Disk
• Bulge

La siguiente imagen muestra una protuberancia esférica central + disco circular. La distribución estelar y de gas es diferente en la protuberancia y el disco.

Cinemática de galaxias espirales

• La velocidad circular de cualquier objeto - Para la protuberancia es (r <Rb).

  $$ V ^ 2 (r) = G \ ast \ frac {M (r)} {r} $$

  $$ M (r) = \ frac {4 \ pi r ^ 3} {3} \ ast \ rho_b $$

• Para el disco - (Rb <r <Rd)

  $$ V ^ 2 (r) = G \ ast \ frac {M (r)} {r} $$

• Bulge tiene una densidad de estrellas aproximadamente constante.

• La densidad dentro de la protuberancia es constante (no cambia con la distancia dentro de la protuberancia).

• En un disco, la densidad estelar disminuye con el radio. El radio aumenta y luego la materia luminosa disminuye.

• A granel - $ V (r) \ propto r $

• En disco - $ V (r) \ propto 1 / \ sqrt {r} $

Curva de rotación de galaxias espirales

• A través de Spectroscopy (galaxias cercanas - la galaxia resuelta espacialmente), producimos la curva de rotación.

• Como se mencionó anteriormente, vemos que la curva de rotación es plana en las regiones externas, es decir, las cosas se mueven rápidamente en las regiones externas, lo que generalmente no se espera que sea de esta forma.

• La velocidad orbital aumenta con el aumento del radio de la región interna, pero se aplana en la región externa.

Materia oscura

Se dice que la Materia Oscura es el Componente No Luminoso del Universo. Entendamos sobre la materia oscura a través de los siguientes consejos.

• Las curvas de rotación planas son contrarias a lo que vemos para la distribución de estrellas y gas en las galaxias espirales.

• La luminosidad de la superficie del disco cae exponencialmente con el radio, lo que implica que la masa de materia luminosa, principalmente estrellas, se concentra alrededor del centro galáctico.

• El aplanamiento de la curva de rotación sugiere que la masa total de la galaxia dentro de algún radio r está aumentando siempre con el aumento de r.

• Esto solo puede explicarse si hay una gran cantidad de masa gravitante invisible en estas galaxias que no emite radiación electromagnética.

• Las medidas de la curva de rotación de las galaxias espirales es uno de los conjuntos de evidencias más convincentes de la materia oscura.

Evidencia de materia oscura

• Masa perdida: 10 veces la masa luminosa.

• La mayor parte de esta materia oscura debe estar en el halo de la galaxia: grandes cantidades de materia oscura en el disco pueden alterar la estabilidad a largo plazo del disco frente a las fuerzas de las mareas.

• Una pequeña fracción de la materia oscura en el disco puede ser bariónica: estrellas tenues (enanas marrones, enanas negras) y remanentes estelares compactos (estrellas de neutrones, agujeros negros). Pero tal materia oscura bariónica no puede explicar la escala completa de masa faltante en las galaxias.

• Perfil de densidad de materia oscura: $ M (r) \ propto r $ y $ \ rho (r) \ propto r ^ {- 2} $.

• Los datos de la curva de rotación de las galaxias espirales son consistentes con la materia oscura distribuida en su halo.

• Este halo oscuro constituye gran parte de la masa total de la galaxia.

• Toda la materia bariónica (estrellas, cúmulos de estrellas, ISM, etc.) se mantiene unida por el potencial gravitacional de este halo de materia oscura.

Conclusión

• La materia oscura solo se ha detectado a través de su interacción gravitacional con una materia ordinaria. Aún no se ha observado interacción con la luz (sin fuerza electromagnética).

• Neutrinos- Carga menos, interactúa débilmente, pero la masa es demasiado menor (<0,23 eV). Las partículas de DM deben tener E> 10 eV más o menos para explicar la formación de la estructura.

• Las partículas masivas de interacción débil (WIMPS) pueden ser la fuente de materia oscura.

Puntos para recordar

• El material más cercano al centro galáctico tiene un período de tiempo más corto.

• Bulge tiene una densidad de estrellas aproximadamente constante.

• La luminosidad de la superficie del disco cae exponencialmente con el radio.

• Grandes cantidades de materia oscura en el disco pueden alterar la estabilidad a largo plazo del disco frente a las fuerzas de las mareas.

La primera evidencia directa de materia oscura provino de Frids Ricky. Hizo algunas observaciones que revelaron materia oscura por primera vez. Sus observaciones consideraron el movimiento general dentro del cúmulo de galaxias.

Los objetos extendidos son cúmulos de galaxias y se consideran estructuras ligadas. Estas galaxias se mueven con respecto al centro del cúmulo pero no vuelan. Observamos el movimiento general de la galaxia.

Supuesto: las velocidades son representativas del potencial subyacente

Cada galaxia tendrá su propio movimiento propio dentro del cúmulo y Hubble Flow Component. Las galaxias más pequeñas son más pequeñas, la mayor parte de la luz proviene de M31 y MW, hay varias galaxias enanas. Para nuestro análisis crudo, solo podemos usar M31 y MW y evaluar la masa dinámica del grupo local.

Hay una velocidad relativa entre nosotros y M31. Es burdo, pero es cierto. La historia comienza hace mucho tiempo cuando M31 y MW estaban cerca el uno del otro, porque eran miembros de un grupo que se estaban alejando el uno del otro. Después de un tiempo alcanzan la máxima separación, luego se acercan el uno al otro.

Digamos que la separación máxima que se puede alcanzar es $ r_ {max} $. Ahora tienen una separación llamadar. DejarMser la masa combinada de MW y M31. No sabemos cuándo se alcanza el $ r_ {max} $.

$$ \ frac {GM} {r_ {max}} = \: Potencial \: en \: r_ {max} $$

Cuando estas galaxias se acercan entre sí en algún instante r, entonces la energía del sistema será ...

$$ \ frac {1} {2} \ sigma ^ 2 = \ frac {GM} {r} = \ frac {GM} {r_ {max}} $$

σ es la velocidad relativa de ambas galaxias. M es solo masa reducida, pero la masa de prueba es 1. σ es la velocidad de cualquier objeto a distancia rdesde el centro del grupo. Creemos que este grupo está en ecuación dinámica porque se cumple el teorema del virial. Entonces, las galaxias no pueden llegar con velocidades diferentes.

¿Cuánto tiempo tardarían estas galaxias en alcanzar la distancia máxima?

Para entender esto, consideremos la siguiente ecuación.

$$ \ frac {1} {2} \ left (\ frac {dr} {dt} \ right) ^ 2 = \ frac {GM} {r} - \ frac {GM} {r_ {max}} $$

$$ t_ {max} = \ int_ {0} ^ {r_ {max}} dt = \ int_ {0} ^ {r_ {max}} \ frac {dr} {\ sqrt {2GM}} \ left (\ frac {1} {r} - \ frac {1} {r_ {max}} \ right) ^ 2 $$

$$ t_ {max} = \ frac {\ pi r_ {max} ^ {\ frac {3} {2}}} {2 \ sqrt {2GM}} $$

Donde, M = masa dinámica del grupo local. El tiempo total desde el inicio hasta el final de la colisión es $ 2t_ {max} $. Por lo tanto,

$$ 2t_ {max} = t_0 + \ frac {D} {\ sigma} $$

Y $ t_0 $ es la edad actual del universo.

Si actual $ t_ {max} <RHS $, entonces tenemos un límite inferior para el tiempo. $ D / \ sigma $ es el momento en que volverán a colisionar. Aquí, asumimos que σ es constante.

$$ t_ {max} = \ frac {t_0} {2} + \ frac {D} {2 \ sigma} $$

$$ r_ {max} = t_ {max} \ times \ sigma = 770K_ {pc} $$

Aquí, σ = velocidad relativa entre MW y M31.

$$ M_ {dynamic} = 3 \ times 10 ^ {12} M_0 $$

$$ M_ {MW} ^ {lum} = 3 \ times 10 ^ {10} M_0 $$

$$ M_ {M31} ^ {lum} = 3 \ times 10 ^ {10} M_0 $$

Pero prácticamente, la masa dinámica se encuentra considerando todas las galaxias dentro del cúmulo. La masa que falta es la materia oscura yFrids Rickynotó que las galaxias en el cúmulo de coma se mueven demasiado rápido. Él predijo la existencia de estrellas de neutrones un año después del descubrimiento de las estrellas de neutrones y utilizó el telescopio Palomar para encontrar la supernova.

Puntos para recordar

• La primera evidencia directa de materia oscura provino de Frids Ricky.

• Los objetos extendidos son cúmulos de galaxias y se consideran bound structures.

• Dynamic mass se descubre considerando todas las galaxias dentro del cúmulo.

En este capítulo, analizaremos los parámetros de densidad y Hubble.

Parámetro de Hubble

El parámetro de Hubble se define de la siguiente manera:

$$ H (t) \ equiv \ frac {da / dt} {a} $$

que mide la rapidez con que cambia el factor de escala. De manera más general, la evolución del factor de escala está determinada por la Ecuación de Friedmann.

$$ H ^ 2 (t) \ equiv \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho - \ frac {kc ^ 2} {a ^ 2} + \ frac {\ wedge} {3} $$

dónde, ∧ es una constante cosmológica.

Para un universo plano, k = 0, por lo tanto, la ecuación de Friedmann se convierte en -

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho + \ frac {\ wedge} {3} $$

Para un universo dominado por la materia, la densidad varía como:

$$ \ frac {\ rho_m} {\ rho_ {m, 0}} = \ left (\ frac {a_0} {a} \ right) ^ 3 \ Rightarrow \ rho_m = \ rho_ {m, 0} a ^ {- 3} $$

y, para un universo dominado por la radiación, la densidad varía como:

$$ \ frac {\ rho_ {rad}} {\ rho_ {rad, 0}} = \ left (\ frac {a_0} {a} \ right) ^ 4 \ Rightarrow \ rho_ {rad} = \ rho_ {rad, 0} a ^ {- 4} $$

Actualmente, vivimos en un universo dominado por la materia. Por lo tanto, considerando $ \ rho ≡ \ rho_m $, obtenemos -

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho_ {m, 0} a ^ {- 3} + \ frac {\ wedge} {3} $$

La constante cosmológica y la densidad de energía oscura están relacionadas de la siguiente manera:

$$ \ rho_ \ wedge = \ frac {\ wedge} {8 \ pi G} \ Rightarrow \ wedge = 8 \ pi G \ rho_ \ wedge $$

De esto, obtenemos -

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ rho_ {m, 0} a ^ {- 3} + \ frac {8 \ pi G} {3} \ rho_ \ wedge $$

Además, la densidad crítica y la constante de Hubble están relacionadas de la siguiente manera:

$$ \ rho_ {c, 0} = \ frac {3H_0 ^ 2} {8 \ pi G} \ Flecha derecha \ frac {8 \ pi G} {3} = \ frac {H_0 ^ 2} {\ rho_ {c, 0}} $$

De esto, obtenemos -

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {H_0 ^ 2} {\ rho_ {c, 0}} \ rho_ {m, 0} a ^ {- 3} + \ frac {H_0 ^ 2} {\ rho_ {c, 0}} \ rho_ \ wedge $$

$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = H_0 ^ 2 \ Omega_ {m, 0} a ^ {- 3} + H_0 ^ 2 \ Omega _ {\ wedge, 0 } $$

$$ (\ dot {a}) ^ 2 = H_0 ^ 2 \ Omega_ {m, 0} a ^ {- 1} + H_0 ^ 2 \ Omega _ {\ wedge, 0} a ^ 2 $$

$$ \ left (\ frac {\ dot {a}} {H_0} \ right) ^ 2 = \ Omega_ {m, 0} \ frac {1} {a} + \ Omega _ {\ wedge, 0} a ^ 2 $$

$$ \ left (\ frac {\ dot {a}} {H_0} \ right) ^ 2 = \ Omega_ {m, 0} (1 + z) + \ Omega _ {\ wedge, 0} \ frac {1} { (1 + z) ^ 2} $$

$$ \ left (\ frac {\ dot {a}} {H_0} \ right) ^ 2 (1 + z) ^ 2 = \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega _ {\ wedge , 0} $$

$$ \ left (\ frac {\ dot {a}} {H_0} \ right) ^ 2 \ frac {1} {a ^ 2} = \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega_ {\ wedge, 0} $$

$$ \ left (\ frac {H (z)} {H_0} \ right) ^ 2 = \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega _ {\ wedge, 0} $$

Aquí, $ H (z) $ es el parámetro de Hubble dependiente del desplazamiento al rojo. Esto se puede modificar para incluir el parámetro de densidad de radiación $ \ Omega_ {rad} $ y el parámetro de densidad de curvatura $ \ Omega_k $. La ecuación modificada es -

$$ \ left (\ frac {H (z)} {H_0} \ right) ^ 2 = \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega_ {rad, 0} (1 + z) ^ 4+ \ Omega_ {k, 0} (1 + z) ^ 2 + \ Omega _ {\ wedge, 0} $$

$$ O, \: \ left (\ frac {H (z)} {H_0} \ right) ^ 2 = E (z) $$

$$ O, \: H (z) = H_0E (z) ^ {\ frac {1} {2}} $$

dónde,

$$ E (z) \ equiv \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega_ {rad, 0} (1 + z) ^ 4 + \ Omega_ {k, 0} (1 + z) ^ 2 + \ Omega _ {\ cuña, 0} $$

Esto muestra que el parámetro de Hubble varía con el tiempo.

Para el Einstein-de Sitter Universo, $ \ Omega_m = 1, \ Omega_ \ wedge = 0, k = 0 $.

Poniendo estos valores, obtenemos -

$$ H (z) = H_0 (1 + z) ^ {\ frac {3} {2}} $$

que muestra la evolución temporal del parámetro de Hubble para el universo de Einstein-de Sitter.

Parámetro de densidad

El parámetro de densidad, $ \ Omega $, se define como la relación entre la densidad real (u observada) ρ y la densidad crítica $ \ rho_c $. Para cualquier cantidad $ x $, el parámetro de densidad correspondiente, $ \ Omega_x $ se puede expresar matemáticamente como -

$$ \ Omega_x = \ frac {\ rho_x} {\ rho_c} $$

Para las diferentes cantidades consideradas, podemos definir los siguientes parámetros de densidad.

S.No.	Cantidad	Parámetro de densidad
1	Bariones	$ \ Omega_b = \ frac {\ rho_b} {\ rho_c} $
2	Materia (bariónica + oscura)	$ \ Omega_m = \ frac {\ rho_m} {\ rho_c} $
3	Energía oscura	$ \ Omega_ \ wedge = \ frac {\ rho_ \ wedge} {\ rho_c} $
4	Radiación	$ \ Omega_ {rad} = \ frac {\ rho_ {rad}} {\ rho_c} $

Donde los símbolos tienen sus significados habituales.

Puntos para recordar

• La evolución del factor de escala está determinada por la Friedmann Equation.

• H(z) es el parámetro de Hubble dependiente del desplazamiento al rojo.

• los Hubble Parameter varía con el tiempo.

• los Density Parameter se define como la relación entre la densidad real (u observada) y la densidad crítica.

Como se discutió en los capítulos anteriores, la evolución temporal del parámetro de Hubble viene dada por:

$$ H (z) = H_0E (z) ^ {\ frac {1} {2}} $$

Dónde z es el corrimiento al rojo y E(Z) es -

$$ E (z) \ equiv \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega (1 + z) ^ 4 + \ Omega_ {k, 0} (1 + z) ^ 2 + \ Omega ^ {\ cuña, 0} $$

Si la expansión del universo es constante, entonces la verdadera edad del universo se da de la siguiente manera:

$$ t_H = \ frac {1} {H_0} $$

Si es el universo dominado por la materia, es decir, el universo de Einstein Desitter, entonces la verdadera edad del universo está dada por:

$$ t_H = \ frac {2} {3H_0} $$

La escala y el desplazamiento al rojo se definen mediante:

$$ a = \ frac {a_0} {1 + z} $$

La edad del universo en términos del parámetro cosmológico se deriva de la siguiente manera.

El parámetro de Hubble viene dado por:

$$ H = \ frac {\ frac {da} {dt}} {a} $$

Diferenciando, obtenemos -

$$ da = \ frac {-dz} {(1 + z) ^ 2} $$

Dónde a₀ = 1 (valor actual del factor de escala)

$$ \ frac {\ mathrm {d} a} {\ mathrm {d} t} = \ frac {-1} {(1 + z) ^ 2} $$

$$ \ frac {\ mathrm {d} a} {\ mathrm {d} t} = \ frac {\ mathrm {d} a} {\ mathrm {d} t} \ frac {\ mathrm {d} z} { \ mathrm {d} t} $$

$$ H = \ frac {\ dot {a}} {a} = \ frac {\ mathrm {d} a} {\ mathrm {d} t} \ frac {\ mathrm {d} z} {\ mathrm {d } t} \ frac {1 + z} {1} $$

$$ \ frac {\ dot {a}} {a} = \ frac {-1} {1 + z} \ frac {\ mathrm {d} z} {\ mathrm {d} t} \ frac {1} { 1} $$

$$ H (z) = H_0E (z) ^ {\ frac {1} {2}} $$

$$ dt = \ frac {-dz} {H_0E (z) ^ {\ frac {1} {2}} (1 + z)} $$

Si queremos encontrar la edad del universo en cualquier corrimiento al rojo dado ‘z’ entonces -

$$ t (z) = \ frac {1} {H_0} \ int _ {\ infty} ^ {z_1} \ frac {-1} {E (z) ^ {\ frac {1} {2}} (1+ z)} dz $$

Dónde k es el parámetro de densidad de curvatura y -

$$ E (z) \ equiv \ Omega_ {m, 0} (1 + z) ^ 3 + \ Omega_ {rad, 0} (1 + z) ^ 4 + \ Omega_ {k, 0} (1 + z) ^ 2 + \ Omega _ {\ cuña, 0} $$

Para calcular la edad actual del universo, tome z₁ = 0.

$$ t (z = 0) = t_ {edad} = t_0 = \ frac {1} {H_0} \ int _ {\ infty} ^ {z_1} \ frac {-1} {E (z) ^ {\ frac { 1} {2}} (1 + z)} dz $$

Para el modelo de Desitter de Einstein, es decir, $ \ Omega_m = 1 $, $ \ Omega_ {rad} = 0 $, $ \ Omega_k = 0 $, $ \ Omega_ \ wedge = 0 $, la ecuación para la edad del universo se convierte en -

$$ t_ {edad} = \ frac {1} {H_0} \ int_ {0} ^ {\ infty} \ frac {1} {(1 + z) ^ {\ frac {5} {2}}} dz $ PS

Después de resolver la integral, obtenemos:

$$ t_H = \ frac {2} {3H_0} $$

El cielo nocturno es como un Cosmic Time Machine.Siempre que observamos un planeta, estrella o galaxia distante, lo estamos viendo como era hace horas, siglos o incluso milenios. Esto se debe a que la luz viaja a una velocidad finita (la velocidad de la luz) y dadas las grandes distancias en el Universo, no vemos los objetos como son ahora, sino como eran cuando se emitió la luz. El tiempo transcurrido entre - cuando detectamos la luz aquí en la Tierra y cuando fue originalmente emitida por la fuente, se conoce comoLookback Time (t_L(z₁)).

Entonces, el tiempo de retroceso viene dado por:

$$ t_1 (z_1) = t_0-t (z_1) $$

El tiempo de retrospectiva del Universo Desitter de Einstein es:

$$ t_L (z) = \ frac {2} {3H_0} \ left [1- \ frac {1} {(1 + z) ^ {\ frac {3} {2}}} \ right] $$

Puntos para recordar

• Siempre que observamos un planeta, estrella o galaxia distante, lo estamos viendo como era hace horas, siglos o incluso milenios.

• El tiempo transcurrido entre el momento en que detectamos la luz aquí en la Tierra y el momento en que fue emitida originalmente por la fuente se conoce como tiempo de retroceso.

En este capítulo, entenderemos qué es la distancia de diámetro angular y cómo ayuda en cosmología.

Para el universo presente -

• $ \ Omega_ {m, 0} \: = \: 0.3 $

• $ \ Omega _ {\ cuña, 0} \: = \: 0.69 $

• $ \ Omega_ {rad, 0} \: = \: 0.01 $

• $ \ Omega_ {k, 0} \: = \: 0 $

Hemos estudiado dos tipos de distancias hasta ahora:

• Proper distance (lp) - La distancia que viajan los fotones desde la fuente hasta nosotros, es decir, la Instantaneous distance.

• Comoving distance (lc) - Distancia entre objetos en un espacio que no se expande, es decir, distance in a comoving frame of reference.

Distancia en función del corrimiento al rojo

Considere una galaxia que irradia un fotón en el momento t₁ que es detectado por el observador en t₀. Podemos escribir la distancia adecuada a la galaxia como:

$$ l_p = \ int_ {t_1} ^ {t_0} cdt $$

Deja que el corrimiento al rojo de la galaxia sea z,

$$ \ Flecha derecha \ frac {\ mathrm {d} z} {\ mathrm {d} t} = - \ frac {1} {a ^ 2} \ frac {\ mathrm {d} a} {\ mathrm {d} t} $$

$$ \ Flecha derecha \ frac {\ mathrm {d} z} {\ mathrm {d} t} = - \ frac {\ frac {\ mathrm {d} a} {\ mathrm {d} t}} {a} \ frac {1} {a} $$

$$ \ por lo tanto \ frac {\ mathrm {d} z} {\ mathrm {d} t} = - \ frac {H (z)} {a} $$

Ahora, comovolver la distancia de la galaxia en cualquier momento t será -

$$ l_c = \ frac {l_p} {a (t)} $$

$$ l_c = \ int_ {t_1} ^ {t_0} \ frac {cdt} {a (t)} $$

En términos de z,

$$ l_c = \ int_ {t_0} ^ {t_1} \ frac {cdz} {H (z)} $$

Hay dos formas de encontrar distancias, que son las siguientes:

Relación flujo-luminosidad

$$ F = \ frac {L} {4 \ pi d ^ 2} $$

dónde d es la distancia a la fuente.

La distancia de diámetro angular de una fuente

Si conocemos el tamaño de una fuente, su ancho angular nos dirá su distancia del observador.

$$ \ theta = \ frac {D} {l} $$

dónde l es la distancia del diámetro angular de la fuente.

• θ es el tamaño angular de la fuente.

• D es el tamaño de la fuente.

Considere una galaxia de tamaño D y tamaño angular dθ.

Lo sabemos,

$$ d \ theta = \ frac {D} {d_A} $$

$$ \ por lo tanto D ^ 2 = a (t) ^ 2 (r ^ 2 d \ theta ^ 2) \ quad \ porque dr ^ 2 = 0; \: d \ phi ^ 2 \ approx 0 $$

$$ \ Flecha derecha D = a (t) rd \ theta $$

Cambiando r a r_c, la distancia comanditaria de la galaxia, tenemos -

$$ d \ theta = \ frac {D} {r_ca (t)} $$

Aquí, si elegimos t = t₀, terminamos midiendo la distancia actual a la galaxia. PeroDse mide en el momento de la emisión del fotón. Por lo tanto, al usart = t₀, obtenemos una distancia mayor a la galaxia y, por lo tanto, una subestimación de su tamaño. Por lo tanto, debemos aprovechar el tiempot₁.

$$ \ por lo tanto d \ theta = \ frac {D} {r_ca (t_1)} $$

Comparando esto con el resultado anterior, obtenemos:

$$ d_ \ cuña = a (t_1) r_c $$

$$ r_c = l_c = \ frac {d_ \ wedge} {a (t_1)} = d_ \ wedge (1 + z_1) \ quad \ porque 1 + z_1 = \ frac {1} {a (t_1)} $$

Por lo tanto,

$$ d_ \ wedge = \ frac {c} {1 + z_1} \ int_ {0} ^ {z_1} \ frac {dz} {H (z)} $$

d_A es la distancia del diámetro angular del objeto.

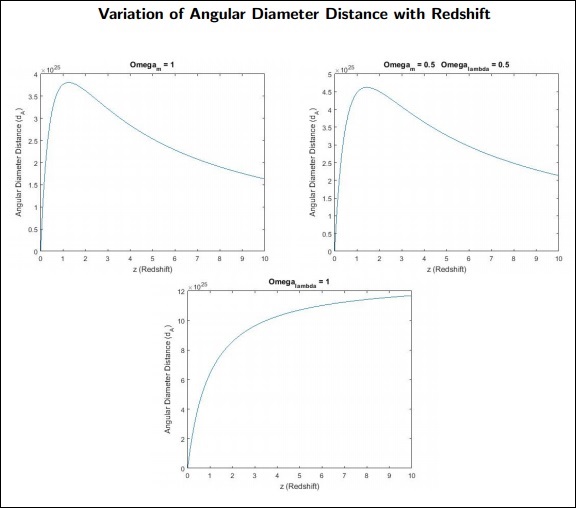
Puntos para recordar

• Si conocemos el tamaño de una fuente, su ancho angular nos dirá su distancia del observador.

• La distancia adecuada es la distancia que viajan los fotones desde la fuente hasta nosotros.

• La distancia comoving es la distancia entre objetos en un espacio que no se expande.

Como se discutió en el capítulo anterior, la distancia del diámetro angular a una fuente en el corrimiento al rojo z está dado por -

$$ d_ \ wedge (z_ {gal}) = \ frac {c} {1 + z_ {gal}} \ int_ {0} ^ {z_ {gal}} \ frac {1} {H (z)} dz $ PS

$$ d_ \ wedge (z_ {gal}) = \ frac {r_c} {1 + z_ {gal}} $$

donde $ r_c $ es la distancia comanditaria.

La distancia de luminosidad depende de la cosmología y se define como la distancia a la que el flujo observado f es de un objeto.

Si se conoce la luminosidad intrínseca $ d_L $ de un objeto distante, podemos calcular su luminosidad midiendo el flujo $ f $ que está determinado por -

$$ d_L (z) = \ sqrt {\ frac {L} {4 \ pi f}} $$

La energía del fotón se desplaza al rojo.

$$ \ frac {\ lambda_ {obs}} {\ lambda_ {emi}} = \ frac {a_0} {a_e} $$

donde $ \ lambda_ {obs}, \ lambda_ {emi} $ se observan y emiten longitudes de onda y $ a_0, a_e $ son factores de escala correspondientes.

$$ \ frac {\ Delta t_ {obs}} {\ Delta t_ {emi}} = \ frac {a_0} {a_e} $$

donde $ \ Delta_t {obs} $ se observa como el intervalo de tiempo de los fotones, mientras que $ \ Delta_t {emi} $ es el intervalo de tiempo en el que se emiten.

$$ L_ {emi} = \ frac {nhv_ {emi}} {\ Delta t_ {emi}} $$

$$ L_ {obs} = \ frac {nhv_ {obs}} {\ Delta t_ {obs}} $$

$ \ Delta t_ {obs} $ tomará más tiempo que $ \ Delta t_ {emi} $ porque el detector debería recibir todos los fotones.

$$ L_ {obs} = L_ {emi} \ left (\ frac {a_0} {a_e} \ right) ^ 2 $$

$$ L_ {obs} <L_ {emi} $$

$$ f_ {obs} = \ frac {L_ {obs}} {4 \ pi d_L ^ 2} $$

Para un universo que no se expande, la distancia de luminosidad es la misma que la distancia comoviva.

$$ d_L = r_c $$

$$ \ Flecha derecha f_ {obs} = \ frac {L_ {obs}} {4 \ pi r_c ^ 2} $$

$$ f_ {obs} = \ frac {L_ {emi}} {4 \ pi r_c ^ 2} \ left (\ frac {a_e} {a_0} \ right) ^ 2 $$

$$ \ Rightarrow d_L = r_c \ left (\ frac {a_0} {a_e} \ right) $$

Estamos encontrando la distancia de luminosidad $ d_L $ para calcular la luminosidad del objeto emisor $ L_ {emi} $ -

• Interpretation - Si conocemos el corrimiento al rojo zde cualquier galaxia, podemos encontrar $ d_A $ ya partir de eso podemos calcular $ r_c $. Esto se usa para averiguar $ d_L $.

• Si $ d_L! = r_c (a_0 / a_e) $, entonces no podemos encontrar a Lemi desde $ f_ {obs} $.

La relación entre la distancia de luminosidad $ d_L $ y la distancia de diámetro angular $ d_A. $

Sabemos que

$$ d_A (z_ {gal}) = \ frac {d_L} {1 + z_ {gal}} \ left (\ frac {a_0} {a_e} \ right) $$

$$ d_L = (1 + z_ {gal}) d_A (z_ {gal}) \ left (\ frac {a_0} {a_e} \ right) $$

El factor de escala cuando se emiten fotones viene dado por:

$$ a_e = \ frac {1} {(1 + z_ {gal})} $$

El factor de escala para el universo actual es -

$$ a_0 = 1 $$

$$ d_L = (1 + z_ {gal}) ^ 2d_ \ wedge (z_ {gal}) $$

¿Cuál elegir $ d_L $ o $ d_A $?

• Para una galaxia de tamaño conocido y desplazamiento al rojo para calcular qué tan grande es, se usa $ d_A $.

• Si hay una galaxia de una magnitud aparente dada, entonces para averiguar qué tan grande es, se usa $ d_L $.

Example - Si se da que dos galaxias de igual desplazamiento al rojo (z = 1) y en el plano del cielo están separadas por 2.3 arc sec entonces, ¿cuál es la máxima separación física entre esos dos?

Para esto, use $ d_A $ de la siguiente manera:

$$ d_A (z_ {gal}) = \ frac {c} {1 + z_ {gal}} \ int_ {0} ^ {z_ {gal}} \ frac {1} {H (z)} dz $$

donde z = 1 sustituye a H (z) según los parámetros cosmológicos de las galaxias.

Puntos para recordar

• La distancia de luminosidad depende de cosmology.

• Si se conoce la luminosidad intrínseca $ d_L $ de un objeto distante, podemos calcular su luminosidad midiendo el flujo f.

• Para un universo que no se expande, la distancia de luminosidad es la misma que la comoving distance.

• La distancia de luminosidad es siempre mayor que la Angular Diameter Distance.

Para cualquier corrimiento al rojo (z) dado, tenemos dos valores para la distancia:

• Distancia de diámetro angular (d _A )
• Distancia de luminosidad (d _L )

No existe una definición única de distancia "cosmológica" en el universo. La elección de la distancia depende del propósito y la conveniencia de la aplicación.

Para probar la tendencia predicha de cómo varía el tamaño angular de un objeto con el corrimiento al rojo, se necesita un criterio de tamaño estándar en el cielo. Este debería ser un objeto que:

• es muy luminoso, por lo que se puede detectar en z> 1.

• es muy grande, por lo que podemos resolver su tamaño angular.

• no ha evolucionado morfológicamente durante un tiempo cosmológicamente significativo (z ∼ 1 corresponde a un tiempo retrospectivo de aproximadamente 7 Gyr).

Algunos objetos (como las galaxias CD) satisfacen los dos primeros criterios. Pero se encuentra que casi todos los objetos evolucionan morfológicamente con el tiempo. En general, los objetos astrofísicos (fuentes extendidas) tienden a ser intrínsecamente más pequeños en el pasado porque todavía se están formando.

Distancia de luminosidad

La distancia de luminosidad depende de la cosmología. La dependencia de la distancia de luminosidad de la cosmología la convierte en una medida útil de los parámetros cosmológicos.

Los parámetros cosmológicos se pueden estimar si podemos encontrar una vela estándar que no evolucione intrínsecamente y que exista desde el universo local al de alto corrimiento al rojo.

Una vela estándar es aquella que no difiere en su luminosidad de una fuente a otra. La premisa es que cualquier diferencia en la luminosidad estimada de las velas estándar debe deberse a la cosmología. Una de esas velas es las supernovas de tipo Ia.

Supernovas de tipo 1a (SNe)

Estos son el resultado de la explosión de una enana blanca después de una acumulación de masa suficiente de su compañera, una gigante roja o estrella de secuencia principal similar, en un sistema binario. Después de que la gigante roja se acerca más que la distancia del lóbulo de Roche de la enana blanca, comienza la transferencia de masa y, finalmente, la enana blanca explota dando una gran cantidad de energía, sin dejar ningún núcleo. Se denominan supernovas de tipo 1a. La tasa típica de explosión de supernovas de tipo 1a en una galaxia es de 1 por siglo.

La búsqueda de SNe de Tipo 1a ha continuado con diferentes equipos:

• Equipo de búsqueda de supernova High z (Brian Schmidt, Adam Reiss et al.)
• Proyecto de cosmología de supernova (Saul Perlmutter et al.)

Ha habido otro equipo de investigación llamado Carnegie Supernovae Project que ha dado resultados similares.

La similitud de los resultados de diferentes equipos muestra la naturaleza cosmológica del SNe de tipo 1a. Por lo tanto, son velas estándar eficientes.

Puntos para recordar

• No existe una definición única de distancia "cosmológica" en el universo.

• La distancia de diámetro angular y la distancia de luminosidad son las más utilizadas.

• Una vela estándar es aquella que no difiere en su luminosidad de una fuente a otra.

• Tipo 1a SNe satisface los criterios de ser una vela estándar.

El CMB (Fondo Cósmico de Microondas) está esencialmente constituido por los fotones de la época en que la materia y la radiación estaban en equilibrio. En la década de 1920, la idea de un universo en expansión fue aceptada y pudo responder a varias preguntas. Pero las preguntas sobre la abundancia de elementos más pesados ​​y la abundancia quedaron sin respuesta. Además, el universo en expansión implicaba que la densidad de la materia debería disminuir hasta 0.

En 1948, George Gammow y Ralph Alpher explicaron el origen de los elementos más pesados ​​y la abundancia usando “Big Bang”. Ellos, junto con Robert Herman, predijeron la existencia de "Radiación Relict" o radiación remanente del "Big Bang". La temperatura prevista para esta radiación remanente estaba entre 50-6 K. En 1965, Robert Dicke, Jim Peebles y David Wilkinson, junto con el Grupo de Investigación de Amo Perizias, detectaron experimentalmente el CMB.

El universo primitivo estaba muy caliente y la energía era demasiado alta para que la materia permaneciera neutral. Por lo tanto, la materia estaba en forma ionizada:Plasma. La Radiación (fotones) y la Materia (plasma) interactuaron principalmente a través de los siguientes tres procesos.

• Compton Scattering - (Proceso de interacción principal) Dispersión inelástica entre un fotón de alta energía y una partícula cargada de baja energía.

• Thomson Scattering - Dispersión elástica de fotones por una partícula cargada libre.

• Inverse Compton Scattering- Partícula cargada de alta energía y fotón de baja energía. Estas interacciones finalmente dieron como resultado que la materia y la radiación estuvieran en equilibrio térmico.

Equilibrio termal

En equilibrio térmico, la radiación obedece a la Planck Distribution of Energy,

$$ B_v (T) = \ frac {2hv ^ 3} {c (e ^ {hv / k_BT} -1)} $$

Durante este tiempo, debido a las interacciones muy frecuentes, el camino libre medio de los fotones fue muy pequeño. El universo era opaco a la radiación. El universo primitivo estaba dominado por la radiación. El universo evolucionó de tal manera que la materia y la radiación alcanzaron el Equilibrio Térmico y su densidad de energía se volvió igual. Esto se puede ver en el gráfico que muestra la evolución de la densidad con el factor de escala. Averigüemos el factor de escala (tiempo) (a (t)) en el que la materia y la radiación alcanzaron el equilibrio.

$$ \ rho_m \ propto \ frac {1} {a ^ 3}, \: \ rho_r \ propto \ frac {1} {a ^ 4} $$

$$ \ frac {\ rho_ {m, t}} {\ rho_ {r, t}} = \ frac {\ Omega_ {m, t}} {\ Omega_ {r, t}} = \ frac {\ Omega_ { m, 0}} {\ Omega_ {r, 0}} a (t) $$

En equilibrio,

$$ \ frac {\ rho_ {m, t}} {\ rho_ {r, t}} = \ frac {\ Omega_ {m, t}} {\ Omega_ {r, t}} = 1 $$

$$ \ Rightarrow \ frac {\ Omega_ {m, 0}} {\ Omega_ {r, 0}} a (t) = 1 \: \ Rightarrow a (t) = 2.96 \ times 10 ^ {- 4} $$

usando $ \ Omega_ {m, 0} = 0.27 $ y $ \ Omega_ {r, 0} = 8 \ times 10 ^ {- 5} $. El corrimiento al rojo correspondiente a este factor de escala viene dado por:

$$ z = 1 / a (t) -1 \ aprox 3375 $$

La densidad de energía de la radiación se redujo debido a la expansión del universo. Así, el universo comenzó a enfriarse. A medida que la energía de los fotones comenzó a disminuir, comenzaron a formarse átomos neutros. Por lo tanto, alrededor de un corrimiento al rojo de 1300, comenzó a formarse hidrógeno neutro. Esta era tenía una temperatura cercana a los 3000K.

La interacción entre la materia y la radiación se volvió muy poco frecuente y, por lo tanto, el universo comenzó a volverse transparente a la radiación. Este período de tiempo se llama“Surface of last scattering”a medida que el camino libre medio de los fotones se hizo muy grande debido a que casi no se produjo ninguna dispersión después de este período. También se llama como“Cosmic Photosphere”.

Puntos para recordar

• El CMB está constituido por los fotones de la época en que la materia y la radiación estaban en equilibrio.

• El universo primitivo era muy caliente y la energía era demasiado alta para que la materia permaneciera neutra, por lo que existía como materia ionizada: Plasma.

• La dispersión de Compton, la dispersión de Thomson y la dispersión de Compton inversa eran los 3 procesos de interacción materia-radiación en ese entonces.

• El universo evolucionó de tal manera que la materia y la radiación alcanzaron el equilibrio térmico.

Primero debemos entender qué caracteriza a la decoupling. Sabemos que las energías eran mucho más elevadas hasta tal punto que la materia sólo existía en forma deIonized Particles. Por lo tanto, en las épocas de desacoplamiento y recombinación, la energía tuvo que disminuir para permitir la ionización del hidrógeno. Se puede realizar un cálculo aproximado a la estimación de la temperatura en el momento del desacoplamiento.

Esto se ha realizado de la siguiente manera:

Primero, considere solo la ionización del hidrógeno en estado fundamental.

$$ hv \ approx k_BT $$

$$ \ por lo tanto T \ approx \ frac {hv} {k_B} $$

Para la ionización del hidrógeno en estado fundamental, hν es 13,6 eV y kB es el Boltzmann Constant8.61 × 10 ⁻⁵ eV / K que revela que la temperatura es 1.5 × 105 kelvin.

Esto esencialmente nos dice que si la temperatura es inferior a 1,5 × 10 ⁵ K, los átomos neutros pueden comenzar a formarse.

Sabemos que la relación de fotones a bariones es de aproximadamente 5 × 10 ¹⁰ . Por tanto, incluso en la cola del gráfico donde se reduce el número de fotones, todavía habrá suficientes fotones para ionizar los átomos de hidrógeno. Además, la recombinación de electrones y protones no garantiza un átomo de hidrógeno en estado fundamental. Los estados excitados requieren menos energía para la ionización. Por lo tanto, se debe realizar un análisis estadístico disciplinado caso por caso para obtener un valor exacto. Los cálculos establecen la temperatura en alrededor de 3000K.

Por el bien de las explicaciones, consideramos el caso de excitar hidrógeno en el primer estado excitado. La expresión general para la relación del número de fotones con energía superior aΔE, Nγ (> ΔE) al número total de fotones Nγ está dado por -

$$ \ frac {N_ \ gamma (> \ Delta E)} {N_ \ gamma} \ propto e ^ {\ frac {- \ Delta E} {kT}} $$

Para el caso de excitar hidrógeno al primer estado excitado, ΔEes de 10,2 eV. Ahora, si consideramos un número muy conservador de al menos 1 fotón con energía superior a 10,2 por cada barión (teniendo en cuenta que la relación es 5 × 10 ¹⁰ , obtenemos la temperatura de la ecuación 3 como 4800 K (Insertado Nγ (> ΔE) = Np).

Esta es la temperatura para crear una población de átomos de hidrógeno neutros en el primer estado excitado. La temperatura para ionizar esto es significativamente menor. Así, obtenemos una mejor estimación que 1,5 × 10 ⁵ K que se acerca más al valor aceptado de 3000 K.

Relación de cambio al rojo - temperatura

Para comprender la relación entre el desplazamiento al rojo y la temperatura, empleamos los dos métodos siguientes, como se describe a continuación.

Método 1

Desde Wien’s Law, lo sabemos

$$ \ lambda_mT = constante $$

Para relacionar esto con el corrimiento al rojo, usamos -

$$ 1 + z = \ frac {\ lambda_0} {\ lambda_e} $$

Como $ λ_oT_o = λ_eT (z) $, obtenemos -

$$ T (z) = T_0 \ frac {\ lambda_0} {\ lambda_e} = T_0 (1 + z) $$

Ajuste T_o como el valor actual 3K, podemos obtener valores de temperatura para un corrimiento al rojo dado.

Método 2

En términos de frecuencia, sabemos:

$$ v_0 = \ frac {v_e} {1 + z} $$

$$ B_vdv = \ frac {2hv ^ 3} {c ^ 2} \ frac {dv} {e ^ {hv / kT} -1} $$

Esto nos dice acerca de la energía neta de los fotones para un intervalo de energía y hνes la energía de un solo fotón. Por tanto, podemos obtener el número de fotones porBνdν/hν.

Si $ n_ {νo} $ es para presente y $ n_ {νe} $ para emitido, obtenemos -

$$ \ frac {n_ {v_e}} {n_ {v_0}} = (1 + z) ^ 3 $$

En simplificación, obtenemos,

$$ n_ {v_0} = \ frac {2v_c ^ 2} {c ^ 2} \ frac {dv_c} {e ^ {hv / kT} -1} \ frac {1} {(1 + z) ^ 3} = \ frac {2v_0 ^ 2} {c ^ 2} \ frac {dv_c} {e ^ {hv / kT} -1} $$

Esto nos da la Wien’s Law de nuevo y así se puede concluir que -

$$ T (z) = T_0 \ frac {\ lambda_0} {\ lambda_e} = T_0 (1 + z) $$

Puntos para recordar

• El universo primitivo estaba muy caliente, K 3000K.
• Las mediciones actuales revelan que la temperatura del universo está cerca de los 3K.
• Cuanto más retrocedemos en el tiempo, la temperatura aumenta proporcionalmente.

En este capítulo, discutiremos la anisotropía de la radiación CMB y COBE, es decir, Cosmic Background Explorer.

Anisotropías primarias en el CMB

Para comprender las observaciones desde el espacio y las anisotropías primarias en la radiación de fondo de microondas cósmica, tomemos las siguientes ecuaciones y comprendamos como se muestra a continuación.

Densidad del número de fotones CMB (n _γ , 0)

$$ n _ {\ gamma, 0} = \ frac {Total \: energía \: densidad} {Característica \: energía \: de \: Fotones} $$

$$ n _ {\ gamma, 0} = \ frac {aT_0 ^ 4} {k_BT_0} $$

Donde $ k_B $ es Boltzmann Constant y $ T_0 $ es el present temperature of the universe.

Usando la temperatura actual $ (T_0) $ como 2.7 K, obtenemos la densidad actual del número de fotones CMB como 400 cm ⁻³ .

La densidad del número de fotones estelares cósmicos es mucho menor (∼ = 10 ⁻³ cm ⁻³ ) en escalas grandes.

Relación barión a fotón (η)

Si las contribuciones estelares de las galaxias, que se mezclan con CMB, son insignificantes, la relación barión a protón es:

$$ \ eta = \ frac {n_ {b, 0}} {n _ {\ gamma, 0}} $$

El valor actual es ∼5 × 10 ⁻¹⁰ . Dado que las densidades de los números de fotones y bariones son proporcionales aa⁻³, luego η no evoluciona con el tiempo.

Densidad de energia

A diferencia de la densidad numérica, la densidad de energía de la materia está más dominada que la densidad de energía de los fotones en la actualidad.

La densidad de energía de la materia bariónica = $ \ rho_ {b, 0} c ^ 2 = 0.04 \ rho_cc ^ 2 = 2 × 10 ^ {- 9} ergcm ^ {- 3} $. Mientras, la densidad de energía de la radiación = $ aT_0 ^ 4 = 4 \ times 10 ^ {- 13} ergcm {−3} $.

Isotropía de la radiación CMB

Penzias y Wilsonencontró que el CMB es isotrópico dentro de los límites de las observaciones. Los límites son la baja resolución angular y la sensibilidad de los instrumentos. Hicieron observaciones desde la tierra, debido a esto, las observaciones no se pueden realizar en todo el espectro ya que el vapor de agua en la atmósfera absorbe muchas longitudes de onda que van desde 1 mm a 1 m. Entonces, CMB no puede afirmarse como un espectro.

Se cree que el CMB es invariante en rotación (isotrópico). Dado que existió una época en la que la materia y la radiación estaban en equilibrio, la formación de estructuras en el universo es inexplicable. Dado que la distribución de la materia no es isotrópica, sino que está agrupada como una red cósmica con enormes vacíos en el medio, se cree que el CMB tiene un origen extragaláctico.

Pero, a medida que comenzaron las observaciones desde el espacio, se encontraron anisotropías en el CMB, lo que lleva a razonar que estas anisotropías en la materia conducen a la formación de estructuras.

Observación de radiación CMB desde el espacio

Los principales satélites que se lanzaron para observar el CMB fueron:

• Cosmic Microwave Background Explorer (COBE, 1989)

• Wilkinson Microwave Anisotropy Probe (WMAP, 2001) y

• Planck (2009).

COBE (Explorador de fondo cósmico)

COBE tenía principalmente dos instrumentos. Ellos eranFar InfraRed Absolute Spectrometer (FIRAS) y Differential Microwave Radiometers(Antenas DMR). FIRAS mide la intensidad del CMB en función de la longitud de onda en cualquier dirección específica. Considerando que, DMR tiene 3 antenas para medir la diferencia de intensidad de CMB desde tres direcciones diferentes. Los siguientes consejos nos brindan más información sobre FIRAS y DMR.

• Las observaciones del CMB de FIRAS muestran que la radiación del CMB corresponde al espectro del cuerpo negro a T = 2.72528 ± 0.00065 K.

• El DMR mide tres frecuencias (31,5 GHz, 53 GHz, 90 GHz) en todas las direcciones del cielo.

• El "símbolo rojo de batman" en las observaciones de DMR es el ruido de la emisión en primer plano (emisión galáctica difusa sincrotrón).

• Las variaciones de intensidad en las observaciones corresponden a variaciones de temperatura. La presencia de puntos calientes y fríos prueba que la radiación CMB es anisotrópica.

• Esta anisotropía debe estar presente en el momento del desacoplamiento ya que no hay distorsiones en CMB. Por tanto, la materia debería tener unos bolsillos con mayor densidad que los demás.

Resultados COBE

El espectro CMB (intensidad en función de la energía) es casi un cuerpo negro perfecto que corresponde a T = 2,7 K. La intensidad específica de la radiación CMB es casi la misma en todas las direcciones. Confirmación de que el universo es isotrópico a gran escala (valida nuestra suposición del principio cosmológico).

El análisis de los datos mostró que hay anisotropías de temperatura ("fluctuaciones") en el espectro de CMB a la resolución de COBE (DMR).

Resolution of COBE, WMAP, Planck

• El instrumento DMR a bordo del COBE tenía una resolución espacial límite (máxima) de ∼ 7 grados.

• La sonda de anisotropía de microondas Wilkinson (WMAP) tenía una resolución promedio de ∼ 0,7 grados.

• El satélite Planck tiene una resolución angular de ∼ 10 minutos de arco.

Puntos para recordar

• La densidad del número de fotones estelares cósmicos es mucho menor que la densidad del número de fotones del CMB.

• Vivimos en un universo dominado por la materia, ya que la densidad de energía de la materia es mayor que la densidad de energía de los fotones.

• COBE, WMAP, Planck son esfuerzos para medir y cuantificar anisotropías en el CMB.

• La formación de estructura en el universo es el resultado de anisotropías CMB.

Cuando miramos el mapa CMB refinado y corregido de todo el cielo, hay mucha contaminación en primer plano, que es una especie de anisotropyen estos mapas. Podemos ver que estas emisiones en primer plano son de la Vía Láctea. La intensidad de CMB es alta a lo largo del plano del plano galáctico y se reduce a medida que nos alejamos. En estos, podemos observar anisotropías secundarias, que son emisiones de sincrotrón de la galaxia. Estas emisiones constituyen la contaminación de primer plano. Para observar la emisión de CMB del cielo, debemos restar estas emisiones de primer plano.

La siguiente imagen muestra el CMB con emisiones en primer plano.

Anisotropía dipolo

Hay otro tipo de anisotropía, que se encontró en el mapa de todo el cielo de CMB, se llama anisotropía dipolo. No está asociado con el universo temprano. Esto se puede representar mediante funciones armónicas esféricas. Si hay un patrón en una superficie esférica y queremos mapearlo usando funciones matemáticas, podemos hacerlo usando funciones trigonométricas. Entonces, cuando mapeamos, puede ser un monopolo, el mismo en todas las direcciones, o un dipolo, que invierte las propiedades cuando se gira 180 grados. Del mismo modo, tenemos cuadrupolo y así sucesivamente. Para un patrón complejo, se puede expresar como la suma de estos monopolos, dipolos, cuadrupolos, etc.

El CMB está modelado de tal manera que una de las principales fuentes de anisotropía en el mapa de todo el cielo es esta anisotropía dipolar, pero no es un modelado primordial del CMB. Esto se puede ver en la siguiente imagen.

La dirección del dipolo que vemos no es una dirección aleatoria. La anisotropía dipolo tiene una dirección. Vemos la intensidad del CMB en una dirección específica. Esta dirección se debe al vector de velocidad del sistema solar. La velocidad de la tierra se puede representar con respecto al sol o al centro de la galaxia. La dirección en la que se mueve la tierra, observamos un desplazamiento al azul y al rojo, y el dipolo se encuentra en esta dirección.

La imagen de arriba tiene una apariencia típica de dipolo porque nuestra galaxia se mueve en una dirección específica. El resultado es: un lado del cielo aparecerá Desplazado al rojo y el otro lado del cielo aparecerá Desplazado al azul. En este caso, Redshifting significa que los fotones son más largos en longitud de onda = más fríos (por lo tanto, al revés de su nombre, se ven azules en el diagrama de arriba).

Podemos decir que la tierra se está moviendo en una dirección específica con respecto al sol / centro galáctico / CMB en el cielo en un instante dado. Entonces, si miramos en cualquier ángulo y medimos la temperatura de CMB, sería diferente. Esto se debe a que estamos midiendo fotones que están desplazados al azul o al rojo y dependen de la línea de visión de los fotones en el cielo.

Puntos para recordar

• La contaminación de primer plano en CMB all sky map se llama anisotropía de CMB.

• Estas emisiones son de nuestra propia galaxia, la vía láctea.

• Los 2 tipos de anisotropías son: anisotropía dipolo y anisotropía del espectro de potencia angular.

• La anisotropía dipolo está en una dirección específica, mientras que la anisotropía del espectro de potencia angular se extiende por todas partes.

La longitud del horizonte es la distancia recorrida por los fotones de luz desde 'The Big Bang' hasta 'The Recombination Era'. El ^primer pico del espectro angular está en θ = 1◦ (l = 180), que es una escala de longitud muy especial.

La distancia adecuada entre dos puntos viene dada por:

$$ r_p = \ int_ {0} ^ {t} cdt $$

Cuando tomamos el marco de tiempo de t = 0 a t = t _rec , entonces

$$ r_H = \ int_ {0} ^ {t_ {rec}} cdt $$

Donde $ r_H $ es la distancia al horizonte adecuada.

Ahora, sabemos que ...

$$ \ dot {a} = \ frac {\ mathrm {d} a} {\ mathrm {d} t} $$

$$ dt = \ frac {da} {\ dot {a}} $$

Cuando t = 0, a = 0.

Entonces $ t = t_ {rec}, a = a_0 / (1 + z_ {rec}) $.

Por lo tanto, podemos escribir,

$$ r_H (z_ {rec}) = \ int_ {0} ^ {a_ {rec}} c \ frac {da} {aH} $$

$$ H (a_ {rec}) = H (z_ {rec}) = H_0 \ sqrt {\ Omega_ {m, 0}} a ^ {- 3/2} $$

Durante el Recombination period universeestaba dominada la materia. es decir,Ωrad << Ωmatter. Por lo tanto, se elimina el término radiación.

$$ r_H (z_ {rec}) = \ frac {c} {H_0 \ sqrt {\ Omega_ {m, 0}}} \ int_ {0} ^ {a_ {rec}} \ frac {da} {a ^ { -1/2}} $$

$$ r_H (z_ {rec}) = \ frac {2c} {3H_0 \ sqrt {\ Omega_ {m, 0}}} \ frac {1} {(1 + z_ {rec}) ^ {3/2}} $$

$$ \ theta_H (rec) = \ frac {r_H (z_ {rec})} {d_A (z_ {rec})} $$

Que es igual a 0.5 grados, si ponemos todos los valores conocidos en la ecuación.

los Electromagnetic radiationes opaco desde la superficie de la última dispersión. Cualquier dos puntos "no" que se encuentren dentro del horizonte uno del otro no necesitan tener las mismas propiedades. Entonces, dará diferentes valores de temperatura.

Podemos obtener dos puntos en esta superficie que no se cruzan entre sí, lo que significa que en un punto el universo se expandió más rápido que la velocidad de la luz, que es el modelo inflacionario de expansión.

Puntos para recordar

• La longitud del horizonte es la distancia recorrida por los fotones de luz desde 'The Big Bang' hasta 'The Recombination Era'.

• Durante el período de Recombinación, el universo estuvo dominado por la materia.

• La radiación electromagnética es opaca desde la superficie de la última dispersión.

Astrobiologyes el estudio del origen, evolución, distribución y futuro de la vida en el universo. Se ocupa de descubrir y detectarExtrasolar Planets.

Astrobiology aborda los siguientes puntos:

• ¿Cómo comienza y evoluciona la vida? (biología + geología + química + ciencias atmosféricas)

• ¿Hay mundos más allá de la tierra que sean favorables para la vida? (astronomía)

• ¿Cuál sería el futuro de la vida en la tierra?

Astronomy aborda los siguientes puntos:

• ¿Cómo detectar el sistema planetario alrededor de otras estrellas?

• Uno de los métodos es la obtención de imágenes directas, pero es una tarea muy difícil porque los planetas son fuentes de luz extremadamente débiles en comparación con las estrellas, y la poca luz que proviene de ellos tiende a perderse en el resplandor de su estrella madre.

• El contraste es mejor cuando el planeta está más cerca de su estrella madre y caliente, de modo que emite una intensa radiación infrarroja. Podemos hacer imágenes en la región infrarroja.

Técnicas para la detección de planetas extrasolares

Las técnicas más eficientes para la detección de planetas extrasolares son las siguientes. Cada uno de estos también se explica en detalle en los capítulos siguientes.

Método de velocidad radial

También se denomina método Doppler. En esto -

• El sistema de planetas estelares gira alrededor de su baricentro, la estrella se bambolea.

• El bamboleo se puede detectar

  • Cambios periódicos de rojo / azul. Astrometría: medir los objetos en el cielo con mucha precisión.

Método de tránsito

El método de tránsito (telescopio espacial Kepler) se utiliza para averiguar el tamaño. La caída en el brillo de una estrella a un planeta suele ser muy inferior, a diferencia de un sistema binario.

Imágenes directas

Imágenes del planeta usando un telescopio.

Veamos un caso de estudio realizado sobre el método de velocidad radial.

Caso de estudio

Este caso de estudio se encuentra en la órbita circular y el plano de la órbita perpendicular al plano del cielo. El tiempo que tardarán ambos alrededor del baricentro será el mismo. Será igual a la diferencia de tiempo entre dos Redshift o Blueshift.

Considere la siguiente imagen.

En A y C, se mide la velocidad máxima. En C, la velocidad es cero.

• Vrmax = V _* es la verdadera velocidad de la estrella.

• P es el período de tiempo de la estrella y del planeta.

• θ es la fase de la órbita.

• Masa de estrella - M _* , radio de órbita a _* , masa del planetam_p.

Desde la ecuación del centro de masa,

$$ m_p a_p = M_ \ ast a_ \ ast $$

De la ecuación de velocidad,

$$ V_ \ ast = \ frac {2 \ pi a_ \ ast} {P} $$

$$ \ Flecha derecha a_ \ ast = \ frac {PV_ \ ast} {2 \ pi} $$

Desde Kepler’s Law,

$$ P ^ 2 = \ frac {4 \ pi ^ 2a_p ^ 3} {GM_ \ ast} $$

$$ \ Rightarrow a_p = \ left (\ frac {P ^ 2GM_ \ ast} {4 \ pi ^ 2} \ right) ^ {1/3} $$

De las ecuaciones anteriores, obtenemos:

$$ \ Rightarrow m_p = \ left (\ frac {P} {2 \ pi G} \ right) ^ {1/3} M_ \ ast ^ {2/3} V_ \ ast $$

Obtenemos: $ m_p, a_p $ y $ a_ \ ast $.

La ecuación anterior está sesgada hacia la mayoría de los planetas masivos cercanos a la estrella.

Puntos para recordar

• La astrobiología es el estudio del origen, evolución, distribución y futuro de la vida en el universo.

• Las técnicas para detectar los planetas extrasolares son: Método de Velocidad Radial, Método de Tránsito, Imagen Directa, etc.

• El bamboleo se puede detectar mediante cambios periódicos de rojo / azul y astrometría.

• El método de velocidad radial está sesgado hacia la detección de planetas masivos cerca de la estrella.

En el capítulo anterior, se discutió el método de velocidad radial para el caso en el que el plano orbital y el plano del cielo son perpendiculares para las órbitas circulares. Aquí, nos ocupamos de un caso más, cuando el plano orbital y el plano del cielo no son perpendiculares para órbitas circulares.

Cuando el plano orbital forma un ángulo con respecto al plano del cielo (no perpendicular), tenemos la siguiente situación:

En este caso, cuando eran perpendiculares, teníamos dos puntos en los que podíamos medir la velocidad real. Pero aquí, eso no es posible. En todos los puntos, podemos medir solo un componente de la velocidad verdadera,v.

$$ v_r = v \: sin (i) cos (\ theta) $$

dónde θes la fase de la órbita que depende del tiempo. El ángulo de inclinaciónipor otro lado, es independiente del tiempo. Por lo tanto,

$$ (v_r) _ {max} = v \: sin (i) $$

La curva de velocidad radial observada tendrá la siguiente forma:

Cuando el plano orbital es perpendicular al cielo -

$$ m_p = \ left (\ frac {P} {2 \ pi G} \ right) ^ {\ frac {1} {3}} (M_ \ ast) ^ {\ frac {2} {3}} v $ PS

dónde m_p, P, G, M∗son la masa del planeta, el período orbital, la constante gravitacional universal y la masa de la estrella, respectivamente. Pero en este caso, deberíamos modificarlo de la siguiente manera:

$$ m_psin (i) = \ left (\ frac {P} {2 \ pi G} \ right) ^ {\ frac {1} {3}} (M_ \ ast) ^ {\ frac {2} {3} } (v_r) _ {max} $$

Pero encontrar el valor de i es una tarea difícil. Podemos imponer ciertas restricciones al valor deiutilizando el método de tránsito. El paso del planeta entre la estrella y la Tierra se llama tránsito. Podemos obtener la curva de luz observando un tránsito y una caída significativa en el flujo observado de una curva de luz implica que i está cerca de los 90 grados. Si tales condiciones no se cumplen, no podemos tener idea del valor dei. Entonces el valor dem_p que encontramos puede servir como un límite inferior para la masa del planeta, ya que en realidad es m_p sin(i) y sin(i) ≤ 1.

Para concluir, el método de velocidad radial es más conveniente que el método de tránsito porque la velocidad radial se puede medir en cualquier momento, pero las mediciones de tránsito se pueden realizar solo durante el tránsito, lo que puede no durar mucho.

Puntos para recordar

• Encontrar la inclinación de la órbita del planeta no se logra mediante el método de velocidad radial.

• El método de velocidad radial es mejor que el método de tránsito porque la velocidad radial se puede medir siempre a diferencia de los tránsitos.

• Los tránsitos son de corta duración y muy fáciles de perder.

El método de tránsito (Kepler Space Telescope)se utiliza para averiguar el tamaño. La caída en el brillo de una estrella por parte de un planeta suele ser menos diferente a un sistema binario.

• F₀ es el flujo de la estrella antes de que el planeta lo oculte.

• F₁ es el flujo después de que todo el planeta está frente a la estrella.

La siguiente imagen se utilizará para todos los cálculos.

$$ \ frac {F_0 - F_1} {F_0} = \ frac {\ pi r_p ^ {2}} {\ pi R ^ 2_ \ ast} $$

$$ \ frac {\ Delta F} {F} \ cong \ frac {r ^ 2_p} {R ^ 2_ \ ast} $$

$$ \ left (\ frac {\ Delta F} {F} \ right) _ {earth} \ cong 0.001 \% $$

$$ \ left (\ frac {\ Delta F} {F} \ right) _ {júpiter} \ cong 1 \% $$

Esto no es fácil de lograr con un telescopio terrestre. Se logra mediante el telescopio Hubble.

Aquí, $ t_T $ es el tiempo entre la posición A y D y $ t_F $ es el tiempo entre la posición B y C.

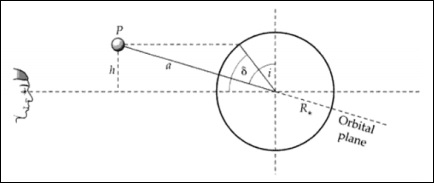
La geometría de un tránsito relacionada con la inclinación. idel sistema. La latitud y la inclinación del tránsito son intercambiables.

De las imágenes de arriba, podemos escribir:

$$ \ frac {h} {a} = cos (i) $$

$$ \ frac {h} {R_ \ ast} = sin (\ delta) $$

$$ cos (i) = \ frac {R_ \ ast sin (\ delta)} {a} $$

$$ y ^ 2 = (R_ \ ast + R_p) ^ 2 - h ^ 2 $$

$$ y = [(R_ \ ast + R_p) ^ 2 - h ^ 2] ^ {\ frac {1} {2}} $$

$$ sin (\ theta) = \ frac {y} {a} $$

$$ \ theta = sin ^ {- 1} \ left [\ frac {(R_ \ ast + R_p) ^ 2 - a ^ 2cos ^ 2 (i)} {a ^ 2} \ right] ^ {\ frac {1 } {2}} $$

$$ t_T = \ frac {P} {2 \ pi} \ times 2 \ theta $$

Aquí, $ t_T $ es la fracción de un período de tiempo durante el cual ocurre el tránsito y (2θ / 2π) es la fracción del ángulo para el cual ocurre el tránsito.

$$ sin (\ frac {t_T \ pi} {P}) = \ frac {R_ \ ast} {a} \ left [\ left (1+ \ frac {R_p} {R_ \ ast} \ right) ^ 2 - \ left (\ frac {a} {R_ \ ast} cos (i) \ right) ^ 2 \ right] ^ {\ frac {1} {2}} $$

Por lo general, a >> R ∗ >> Rp. Entonces, podemos escribir -

$$ sin (\ frac {t_T \ pi} {P}) = \ frac {R_ \ ast} {a} \ left [1- \ left (\ frac {a} {R_ \ ast} cos (i) \ right ) ^ 2 \ right] ^ {\ frac {1} {2}} $$

Aquí, Pes la duración entre dos tránsitos sucesivos. El tiempo de tránsito es muy inferior al del período orbital. Por lo tanto,

$$ t_T = \ frac {P} {\ pi} \ left [\ left (\ frac {R_ \ ast} {a} \ right) ^ 2 - cos ^ 2 (i) \ right] ^ {\ frac {1 } {2}} $$

Aquí, t_T, P, R∗ son los observables, a y i debe ser averiguado.

Ahora,

$$ sin (\ frac {t_F \ pi} {P}) = \ frac {R_ \ ast} {a} \ left [\ left (1 - \ frac {R_p} {R_ \ ast} \ right) ^ 2 - \ left (\ frac {a} {R_ \ ast} cos \: i \ right) ^ 2 \ right] ^ {\ frac {1} {2}} $$

donde, $ y ^ 2 = (R_ \ ast - R_p) ^ 2 - h ^ 2 $.

Dejar,

$$ \ frac {\ Delta F} {F} = D = \ left (\ frac {R_p} {R_ \ ast} \ right) ^ 2 $$

Ahora, podemos expresar

$$ \ frac {a} {R_ \ ast} = \ frac {2P} {\ pi} D ^ {\ frac {1} {4}} (t ^ 2_T - t ^ 2_F) ^ {- \ frac {1 } {2}} $$

Para las estrellas de la secuencia principal,

$$ R_ \ ast \ propto M ^ \ alpha_ \ ast $$

$$ \ frac {R_ \ ast} {R_0} \ propto \ left (\ frac {M_ \ ast} {M_0} \ right) ^ \ alpha $$

Esto da R∗.

Por lo tanto, también obtenemos el valor de 'a'.

Entonces, obtenemos 'R _p ', 'ap' e incluso 'i'.

Para todo esto,

$$ h \ leq R_ \ ast + R_p $$

$$ a \: cos \: i \ leq R_ \ ast + R_p $$

Incluso para ~ 89 grados, la duración del tránsito es muy pequeña. El planeta debe estar muy cerca para conseguir un tiempo de tránsito suficiente. Esto da una restricción estricta a 'i'. Una vez que obtenemos 'i', podemos derivar 'm _p ' de la medición de la velocidad radial.

Esta detección por el método de tránsito se denomina detección aleatoria, es decir, probabilidad de observar un tránsito. Los cálculos de probabilidad de tránsito (probabilidad de observación) se muestran a continuación.

La probabilidad de tránsito está relacionada con el ángulo sólido trazado por las dos configuraciones de tránsito extremas, que es:

$$ Sólido \: ángulo \: del \: planeta \: = 2 \ pi \ left (\ frac {2R_ \ ast} {a} \ right) $$

Además del ángulo sólido total en un semieje mayor a, o -

$$ Sólido \: ángulo \: de \: esfera \: = \: 4 \ pi $$

La probabilidad es la razón de estas dos áreas:

$$ = \: \ frac {área \: de \: cielo \: cubierta \: por \: orientación \: favorable} {área \: \: cielo \: cubierta \: por \: todo \: posible \: orientación \: de \: órbita} $$

$ = \ frac {4 \ pi a_pR_ \ ast} {4 \ pi a ^ 2_p} = \ frac {R_ \ ast} {a_p} $ $ \ frac {área \: de \: hueco \: cilindro} {área \ : de \: esfera} $

Esta probabilidad es independiente del observador.

Puntos para recordar

• El método de tránsito (telescopio espacial Kepler) se utiliza para averiguar el tamaño.
• La detección por el método de tránsito es una detección casual.
• El planeta debe estar muy cerca para tener suficiente tiempo de tránsito.
• La probabilidad de tránsito está relacionada con el ángulo sólido del planeta.
• Esta probabilidad es independiente del marco de referencia del observador.

La primera imagen directa de un planeta extrasolar, en 2004, fue de un planeta de masa 3-10 M_jupiter orbitando alrededor de una enana marrón (2M1207) con una masa de 25 M_jupiter. Para la detección de exoplanetas se han utilizado técnicas como la velocidad radial, el tránsito, la microlente gravitacional, la obtención de imágenes, la astrometría, etc. El número de detecciones ha aumentado cada año.

Hasta alrededor de 2010, el método de velocidad radial se usaba ampliamente, pero ahora la mayoría de las detecciones se realizan mediante el método de tránsito. Hubo un aumento en el número de detecciones en 2014, que fue cuandoKepler Space Telescope (KST) comenzó a dar los resultados.

Una distribución de período de masa muestra que el método de velocidad radial está más sesgado hacia la detección de planetas masivos con un período más grande, mientras que con el método de tránsito, los planetas con un período más bajo solo se detectan como se muestra en la siguiente imagen (Cortesía: NASA Exoplanet Archive) .

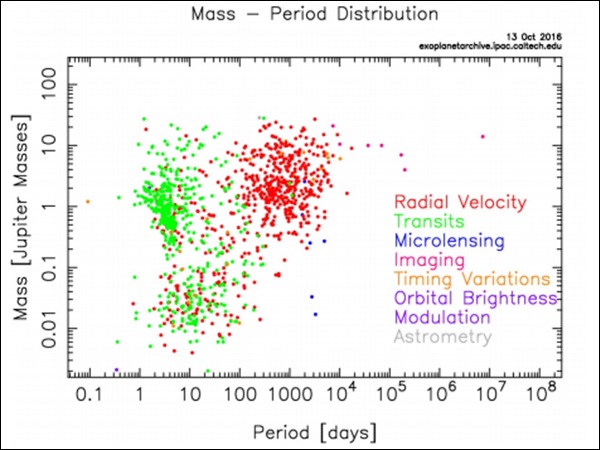
Hay un aumento colosal en el número de detecciones de planetas de masa más pequeña desde el advenimiento de KST. Esto es evidente en la figura que se muestra a continuación. Los planetas detectados por KST se dividen en dos grupos: planetas calientes masivos llamados "Júpiter calientes" y planetas de menor masa llamados "Súper Tierras calientes" (ya que son más masivos que la Tierra).

Cuando graficamos el número de planetas extrasolares detectados frente a la distancia a ellos, encontramos que la mayoría de estos planetas están dentro de 2 kpc, lo cual está dentro de nuestra galaxia. Quizás los planetas no sean tan infrecuentes en el universo, ya que nuestra detección se limita solo a cierto tipo de planetas en una parte muy pequeña del universo.

Los planetas se forman a partir de circumstellar disc o proto planetary disc. Si los planetas se forman como un subproducto durante la formación de estrellas, ¡¡quizás el número de planetas en el universo exceda el número de estrellas en el universo !!

Zonas habitables

Una Zona Habitable se puede definir como la zona alrededor de la estrella donde el agua puede existir en su forma líquida. Considere un planeta a una distancia $ a_p $ de la estrella como se muestra en la siguiente figura. A continuación se describe un método sencillo para calcular la temperatura del planeta.

$$ \ left (\ frac {L_ \ ast} {4 \ pi a ^ 2_p} \ right) \ pi R ^ 2_p (1 - A) = 4 \ pi R ^ 2_p \ sigma T ^ 4_p $$

y

$$ \ frac {L_ \ ast} {4 \ pi R ^ 2_ \ ast} = \ sigma T ^ 4_ \ ast $$

$$ \ por lo tanto T_p = (1 - A) T_ \ ast \ sqrt {\ frac {R_ \ ast} {2a_p}} $$

En nuestro caso sustituyendo

• L_sun = 3.83 x 10²⁶

• a_p = 1.5 ∗ 10¹¹ and

• A = 0.3

Dará $ T_ {Earth} = 255K $. El cálculo real es muy complicado, lo que incluye la física de las nubes. La zona habitable de nuestro sistema solar se encuentra entre 0,9 AU y 1,7 AU.

Se encontró que la luminosidad del Sol aumentaba con el tiempo debido a la disminución de la presión del gas. Era un 30% menos brillante cuando comenzó a quemar hidrógeno. Esto resultaría en un desplazamiento de la zona habitable lejos del Sol. Dado que la Tierra está cerca del borde interior de la zona habitable, ¡quizás algún día se mueva fuera de la zona!

Zona continuamente habitable

En resumen, se denomina CHZpuede definirse como la región en la que puede existir agua líquida durante toda la vida útil de la secuencia principal de una estrella. El KST ha detectado muchos planetas extrasolares que se encuentran en la zona habitable.

Una firma biológica es cualquier sustancia, como un elemento, isótopo, molécula o fenómeno que proporciona evidencia científica de la vida pasada o presente. Un ejemplo es la detección de O ₂ y CO ₂ en un planeta, lo que normalmente no es posible mediante procesos geológicos únicamente. Esta detección se realiza analizando los espectros de absorción.

Puntos para recordar

• Se han utilizado técnicas como velocidad radial, tránsito, microlente gravitacional, imágenes, astrometría, etc. para la detección de exoplanetas.

• El método de velocidad radial está más sesgado hacia la detección de planetas masivos con un período más largo.

• Los planetas calientes masivos se denominan "Hot Júpiter" y los planetas de menor masa se denominan "Hot Super Earths".

• El número de planetas del universo supera el número de estrellas del universo.

• Una zona habitable se puede definir como la zona alrededor de la estrella donde el agua puede existir en su forma líquida.