Razonamiento - Números binarios codificados
El número que tiene base 2 se conoce como número binario. El número binario está formado por los complementos de 0 y 1. Entonces, el número binario codificado consta de dos procesos. Uno es la conversión de binario a decimal y otro es de decimal a binario.
Numeros decimales
Saber qué binary numberes decir, primero tenemos que conocer los números decimales. Entonces, el número decimal consta de diez dígitos (es decir, 0,1,2,3,4,5,6,7,8,9). Cualquier sistema decimal se puede representar usando estos números. Por ejemplo, una secuencia de dígitos es 2, 4, 6 y 8. Lo hacemos de la siguiente manera:
2468 = 2 × 10 3 + 4 × 10 2 + 6 × 10 1 + 8 × 10 0
= 2468
Note- Obtenemos el valor de los números en este caso multiplicando diferentes dígitos de secuencia por potencias de 10 y sumando. Aquí este 10 se llama base o raíz. Por lo tanto, bajo un sistema decimal nuestra base es 10.
Numeros binarios
Usamos diez dígitos para representar un decimal number; así usamos solo dos dígitos para representar un número binario. Cualquier número se puede representar usando estos dos dígitos, es decir, 0 y 1.
Ejemplo de un número binario es 1101. Aquí hay 4 dígitos presentes en la secuencia de dígitos: 1, 1, 0, 1. Obtenemos el valor de la siguiente manera.
1101 = 1 × 2 3 + 1 × 2 2 + 0 × 2 1 + 1 × 2 0
= 8 + 4 + 0 + 1 = 13
Por lo tanto, el número binario representa trece en sistema decimal. El valor se puede determinar mediantemultiplying different digits de secuencia por potencias de 2 y sumando.
Conventional method - En el ejemplo anterior, vemos que para obtener el valor de cualquier número binario, usamos la siguiente regla -
El primer dígito de la derecha se multiplica por 2 0 = 1
El segundo dígito de la derecha se multiplica por 2 1 = 2
El tercer dígito de la derecha se multiplica por 2 2 = 4
De manera similar, el n- ésimo dígito de la derecha se multiplica por 2 n − 1
Finalmente, se agregan todos estos.
For Example - Convierta los siguientes números binarios en números decimales.
A - 1010
B - 1111
C - 100
D - 10000
Solution -
A - 1010 = 1 × 2 3 + 0 × 2 2 + 1 × 2 1 + 0 × 2 0
B - 1111 = 1 × 2 3 + 1 × 2 2 + 1 × 2 1 + 1 × 2 0
C - 100 = 1 × 2 2 + 0 × 2 1 + 0 × 2 0
D - 10000 = 1 × 2 4 + 0 × 2 3 + 0 × 2 2 + 0 × 2 1 + 0 × 2 0
Método más rápido
Step I- Empezando por el dígito derecho del número dado, escriba 1, 2, 4, 8, 16, 32 ……. y así sucesivamente debajo de cada dígito a medida que avanza hacia la izquierda.
Step II- Ignore los números por debajo de 0. Suma todos los números por debajo de los 1.
Resolvamos el ejemplo 1 con este método.
A - 1010
Usaremos 1,2,4,8 porque aquí hay 4 dígitos.
Obtenemos,
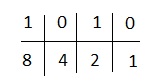
4 y 1 caen por debajo de los ceros. Los ignoramos y sumamos el resto. Obtenemos 8 + 2 = 10
Así podemos resolver otros números.
El número decimal se puede convertir a binario mediante el método de successive divisions. Cada vez que se divide, el dividendo se divide por 2. Se anota el recordatorio y el cociente se convierte en el siguiente dividendo, que nuevamente se divide por 2. El proceso se repite hasta que no sea posible más división.
Por ejemplo, convierta 17 en un número binario -
Divida 17 entre 2 hasta que no sea posible más división.
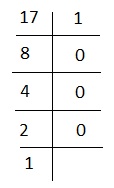
Entonces, la forma binaria de 17 es 10001.
Direction (Q. 1-4) − Study the following question and give the answer.
En cierto código, el símbolo de 0 es + y de 1 es #. Ningún número o símbolo es mayor que 1. El valor del símbolo para 1 se duplica cada vez que se desplaza un lugar hacia la izquierda.
'0' se representa como +
'1' se representa como #
'2' se representa como # +
'3' se representa como ##
'4' se representa como # ++ y así sucesivamente
1 - ¿Cuál de los siguientes representará 11?
Options -
A - # + ##
B - + ## +
C - ## ++
D - # + # ++
E - ninguno de esos
Answer - Opción A
Explanation - Para obtener el equivalente de 11, usamos el método de división sucesiva por 2.

Entonces la forma binaria será 10111. Reemplazando 1 y 0 por # y + obtendremos # + ##.
2 - ¿Cuál de los siguientes representará 8?
Options -
A - ## ++
B - + ## +
C - ## ++
D - ++ ##
E - ninguno de esos
Answer - Opción E
Explanation - para 8, tenemos-
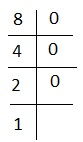
es decir, 1000 o # +++. La elección correcta es 5.
3 - ¿Cuál de los siguientes estará representado por ## + #?
Options -
A - 8
B - 11
C - 13
D - 12
E - ninguno de esos
Answer - Opción E
Explanation- ## + # = 1101 = 1 × 2 3 + 1 × 2 2 + 0 × 2 1 + 1 × 2 0 = 15
4 - ¿Cuál de los siguientes números estará representado por # +++ #?
Options -
A - 22
B - 31
C - 14
D - 17
E - ninguno de esos
Answer - Opción D
Explanation - # + + + # = 10001
= 1 × 2 4 + 0 × 2 3 + 0 × 2 2 + 0 × 2 1 + 1 × 2 0
= 16 + 1 = 17
Los sistemas binarios tienen base 2, un sistema decimal tiene base 10 y el sistema terciario tiene base 3, mientras que el sistema octal tiene base 8. En el caso del terciario, tenemos tres dígitos para representar números. Estos son 0, 1 y 2. En este caso, los números se convertirán a decimales multiplicando con las potencias apropiadas de 3.
For Example -
(12012) 3 = 1 × 3 4 + 2 × 3 3 + 0 × 3 2 + 1 × 3 1 + 2 × 3 0 = (104) 3