Razonamiento: cubo y cuboide
Hoy en día, las preguntas basadas en 'Cubos y Cuboides' se formulan en casi todos los exámenes competitivos. Estos problemas son muy frecuentes en varios concursos.
Los métodos que se describen a continuación son simples pero elegantes. Deben ser muy fáciles de entender y con un poco de práctica debes dominarlos. Un cubo es un sólido tridimensional que tiene 6 caras, 12 aristas y esquinas. Todas las aristas de un cubo son iguales y todas las caras tienen forma cuadrada. Esa es una figura sólida que tiene 6 caras; cada cara que es un cuadrado se llamaa cube. Si cada una de las seis caras es un rectángulo, se llamacuboid. Un cuboide también se llamarectangular parallelepiped.
Las preguntas formuladas sobre cubo y cuboides pueden ser de los siguientes tipos.
Tipo i
Se dan varias vistas de un cubo completo y debe encontrar qué parte del cubo se encuentra exactamente debajo de una parte en particular.
Tipo II
Se da un cubo abierto y tienes que predecir cómo se verá cuando se cierre en un cubo.
Tipo III
Un cubo no se puede barnizar en algunas de sus caras con el mismo color o con colores diferentes y luego cortar en un cierto número específico de piezas idénticas. Luego pregunta de la forma: "¿cuántos cubos pequeños tienen 2 caras barnizadas?" "¿Cuántos cubos pequeños tienen una sola cara barnizada?" etc.
Hay dos tipos de problemas que aparecen en el examen. Al principio, se le ofrecen varias vistas de uncomplete cubey debe indicar qué parte del cubo se encuentra exactamente debajo de una parte en particular. En otro tipo, se le da unaopened-up cube, y tiene que predecir cómo se verá cuando se cierre en un cubo.
For Example -
A continuación se muestran varias caras de un cubo:

¿Qué número estaría opuesto al 2?
A - 1
B - 6
C - 5
D - 4
El enfoque fundamental es el siguiente:
Tipo i
A fundamental rule: Opposite cannot be together;
Siempre que vemos un cubo, con solo tres de sus caras visibles para nosotros, nunca podemos ver dos caras opuestas juntas. Con todas estas reglas, podemos resolver fácilmente el tipo de problema discutido anteriormente. En la pregunta anterior donde tenemos que encontrar la cara opuesta de una cara en particular, podemos eliminar aquellas caras que han aparecido junto con X en cualquier vista. Por lo tanto, podemos eliminar todas las demás opciones y quedarnos será nuestra respuesta.
En este punto, debe volver a leer el párrafo anterior y ver que comprende el concepto. Después de esto, debe intentar resolver el ejemplo anterior y ver si puede aplicar el concepto discutido anteriormente. Sin embargo, descubre que no ha entendido completamente el concepto, no hay problema. Continúe leyendo esta sección. Las cosas se aclararán una vez que termine la sección. Con la regla fundamental anterior en el fondo de su mente, puede resolver el tipo de pregunta anterior.
Para la pregunta, la regla es suficiente en sí misma. Después de eso, puede resolverlo más rápidamentethree secondary rules.
Solution for above example -
En el ejemplo dado, tenemos que encontrar la cara opuesta a 2. Ahora, en la primera figura, aparece 2 junto con 1 y 3. Significa que ni 1 ni 3 pueden ser opuestos a 2. Significa que opuesto a 1 podemos tiene 4 o 5 o 6. De manera similar, frente a 3 podemos tener 4 o 5 o 6. Ahora, mire la segunda figura. Aquí, 3 y 1 ocurren junto con 5. Significa que 5 no es opuesto ni a 3 ni a 1. Entonces, significa que 4 o 6 es opuesto a 1 y otro es opuesto a 3 por lo que 5 debe ser opuesto a 2. Por lo tanto, 5 es correcto responder.
Algunas reglas más rápidas
Ahora debe haber entendido el truco básico para resolver tales preguntas. El truco consiste en eliminar aquellas opciones que no son posibles. Para esto, se toma la ayuda de la regla fundamental que dice que si dos caras son opuestas entre sí, su ocurrencia simultánea en una vista del cubo no es posible. Sin embargo, en las competencias preciadas en el tiempo de hoy, simplemente el concepto no es suficiente. Debe poder resolver una pregunta rápidamente. Hay algunas reglas secundarias para resolver preguntas.
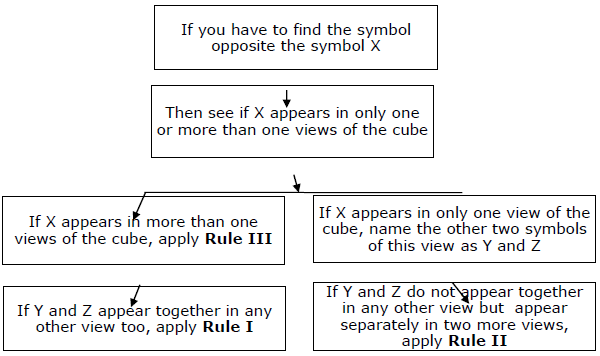
Rule I- Llamemos a esa figura X, cuyo opuesto tienes que encontrar. Suponga que en cualquier vista del cubo, X aparece con Y y Z. Junto con una tercera figura (digamos A), entonces X estará enfrente de A.
Entonces, por ejemplo, tienes que encontrar la cara opuesta a 2. (Esta es nuestra X). Ahora, 2 aparece en una figura junto con 1 y 3. (Y y Z). También 1 y 3 aparecen juntos en una figura más, junto con 5. (Eso es A). Por tanto, 2 debe ser opuesto a 5.
Rule II- Tenemos que encontrar la cara opuesta de 'X'. Suponga que en cualquier vista del cubo, X aparece con Y y Z. Ahora, suponga que Y y Z no aparecen juntos en más vistas, pero aparecen por separado en dos o más vistas diferentes. Entonces, la figura común entre las dos vistas más en las que Y y Z aparecen por separado, será la figura opuesta a X.
Rule III- Llamemos a la figura X, cuyo opuesto tienes que encontrar. Ahora, suponga que X aparece en dos vistas y en estas dos vistas se ven cuatro figuras diferentes con X. Entonces, la única figura que no se ve con X en estas dos vistas debe ser opuesta a X.
Summary- Tienes que mantener la regla fundamental en el fondo de tu mente y luego aplicar tres reglas secundarias para obtener respuestas rápidas. El enfoque completo se puede resumir en el siguiente diagrama.
Tipo II
En este tipo, usamos la regla fundamental. Esta regla nos ayuda a eliminar aquellas combinaciones donde las caras opuestas se muestran en una sola vista. Por lo tanto, conducirá a la eliminación de una elección siempre que sepamos cómo determinar qué caras serán opuestas entre sí, mirando el "opened-up cube”. Para este propósito, existe una regla muy simple con la que puede saberlo mirando elopened-up cube, cuyas caras estarán opuestas entre sí con solo mirarlo.
La regla se da a continuación;
Third is opposite rule -
Cuando desee encontrar la cara opuesta de una cara (digamos X), en la figura I, II, III; se da un cubo abierto. Tenemos que encontrar qué caras están opuestas cuando el cubo está cerrado.
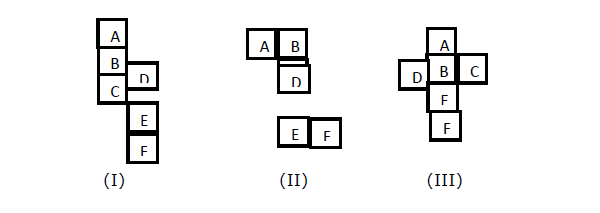
Explanation -
En la figura (I), la tercera figura de A es C. Entonces A es opuesto a C. Entonces, D y F serán opuestos. B y E serán opuestos.
En la figura (II), B es el tercero de D, por lo que B será opuesto a D. De manera similar, C será opuesto a E y A será opuesto a F.
En la figura (III), A es opuesto a E, B es opuesto a F. Por lo tanto, C es opuesto a D.
Steps to solve problem
Ahora podemos resolver cuestiones de este tipo. Sabemos cómo encontrar la cara opuesta mirando unOpened-up cube. También sabemos que en cualquier vista del cubo, las caras opuestas no pueden estar juntas. Por lo tanto, combinando dos reglas, podemos resolver problemas fácilmente.
Resumen
Con esto, se completa la discusión sobre cómo resolver cuestiones de tipo II. Tienes que usar la tercera regla para determinar qué caras son opuestas entre sí. El siguiente diagrama proporcionará la información completa sobre este enfoque.

Tipo III
Counting of Cubes (when a varnished solid cube is cut);
En la sección anterior, discutimos el problema de encontrar la cara opuesta de un cubo. Existe otro tipo de pregunta relacionada con los cubos en la que un cubo más grande con diferentes colores barnizados en diferentes lados, se rompe en varios cubos más pequeños y hay que encontrar el número de cubos que tienen solo un lado barnizado o dos lados barnizados.
Format of this problem -
Example -
Un cubo está barnizado con tres colores verde, azul y rojo en sus lados, con cada color barnizado en dos caras opuestas del cubo. Ahora el cubo se divide en 64 cubos de igual tamaño. Con base en esta información, responda las siguientes preguntas:
1. ¿Cuántos cubos tienen dos lados barnizados y el resto sin barnizar?
A - 18
B - 20
C - 22
D - 24
2. ¿Cuántos cubos tienen un solo lado barnizado (solo de color verde o azul)?
A - 4
B - 24
C - 16
D - 12
3. ¿Cuántos cubos no tienen los lados barnizados?
A - 0
B - 8
C - 12
D - 64