Sirkuit Digital - Metode K-Map
Pada bab sebelumnya, kita telah menyederhanakan fungsi Boolean menggunakan postulat dan teorema Boolean. Ini adalah proses yang memakan waktu dan kami harus menulis ulang ekspresi yang disederhanakan setelah setiap langkah.
Untuk mengatasi kesulitan ini, Karnaughmemperkenalkan metode penyederhanaan fungsi Boolean dengan cara yang mudah. Metode ini dikenal dengan metode peta Karnaugh atau metode K-map. Ini adalah metode grafis, yang terdiri dari 2 n sel untuk variabel 'n'. Sel yang berdekatan dibedakan hanya dalam posisi bit tunggal.
K-Maps untuk 2 hingga 5 Variabel
Metode K-Map paling cocok untuk meminimalkan fungsi Boolean dari 2 variabel menjadi 5 variabel. Sekarang mari kita bahas tentang K-Maps untuk 2 sampai 5 variabel satu per satu.
2 Variabel K-Map
Jumlah sel dalam 2 variabel K-map adalah empat, karena jumlah variabel adalah dua. Gambar berikut menunjukkan2 variable K-Map.
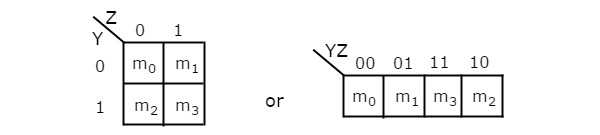
Hanya ada satu kemungkinan untuk mengelompokkan 4 suku min yang berdekatan.
Kombinasi yang mungkin dari pengelompokan 2 suku min yang berdekatan adalah {(m 0 , m 1 ), (m 2 , m 3 ), (m 0 , m 2 ) dan (m 1 , m 3 )}.
3 Variabel K-Map
Jumlah sel dalam 3 variabel K-map adalah delapan, karena jumlah variabel adalah tiga. Gambar berikut menunjukkan3 variable K-Map.
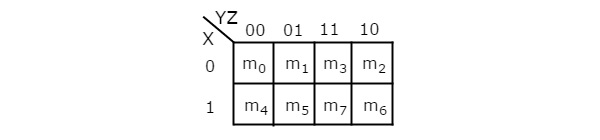
Hanya ada satu kemungkinan untuk mengelompokkan 8 suku min yang berdekatan.
Kemungkinan kombinasi pengelompokan 4 suku min yang berdekatan adalah {(m 0 , m 1 , m 3 , m 2 ), (m 4 , m 5 , m 7 , m 6 ), (m 0 , m 1 , m 4 , m 5 ), (m 1 , m 3 , m 5 , m 7 ), (m 3 , m 2 , m 7 , m 6 ) and (m 2 , m 0 , m 6 , m 4 )}.
Kombinasi yang mungkin dari pengelompokan 2 suku min yang berdekatan adalah {(m 0 , m 1 ), (m 1 , m 3 ), (m 3 , m 2 ), (m 2 , m 0 ), (m 4 , m 5 ) , (m 5 , m 7 ), (m 7 , m 6 ), (m 6 , m 4 ), (m 0 , m 4 ), (m 1 , m 5 ), (m 3 , m 7 ) and ( m 2 , m 6 )}.
Jika x = 0, maka 3 variabel K-map menjadi 2 variabel K-map.
4 Variabel K-Map
Jumlah sel dalam 4 variabel K-map adalah enam belas, karena jumlah variabelnya empat. Gambar berikut menunjukkan4 variable K-Map.
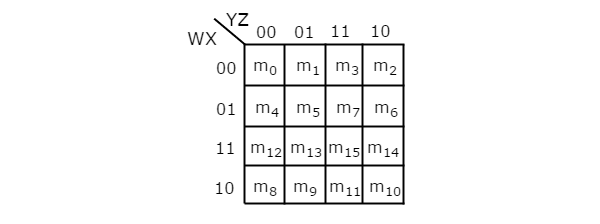
Hanya ada satu kemungkinan untuk mengelompokkan 16 suku min yang berdekatan.
Misal R 1 , R 2 , R 3 dan R 4 masing-masing mewakili suku-suku min dari baris pertama, baris kedua, baris ketiga dan keempat. Demikian pula, C 1 , C 2 , C 3 dan C 4 masing-masing mewakili suku-suku min dari kolom pertama, kolom kedua, kolom ketiga dan kolom keempat. Kombinasi yang mungkin dari pengelompokan 8 suku min yang berdekatan adalah {(R 1 , R 2 ), (R 2 , R 3 ), (R 3 , R 4 ), (R 4 , R 1 ), (C 1 , C 2 ) , (C 2 , C 3 ), (C 3 , C 4 ), (C 4 , C 1 )}.
Jika w = 0, maka 4 variabel K-map menjadi 3 variabel K-map.
5 Variabel K-Map
Jumlah sel dalam 5 variabel K-map adalah tiga puluh dua, karena jumlah variabel adalah 5. Gambar berikut menunjukkan 5 variable K-Map.

Hanya ada satu kemungkinan untuk mengelompokkan 32 suku min yang berdekatan.
Ada dua kemungkinan untuk mengelompokkan 16 suku min yang berdekatan. yaitu, pengelompokan suku-suku min dari m 0 ke m 15 dan m 16 ke m 31 .
Jika v = 0, maka 5 variabel K-map menjadi 4 variabel K-map.
Di atas semua K-maps, kami hanya menggunakan notasi istilah min. Demikian pula, Anda dapat menggunakan notasi istilah Max secara eksklusif.
Meminimalkan Fungsi Boolean menggunakan K-Maps
Jika kita mempertimbangkan kombinasi input yang fungsi Booleannya adalah '1', maka kita akan mendapatkan fungsi Boolean, yaitu di standard sum of products bentuk setelah menyederhanakan K-map.
Demikian pula, jika kita mempertimbangkan kombinasi input yang fungsi Booleannya adalah '0', maka kita akan mendapatkan fungsi Boolean, yaitu di standard product of sums bentuk setelah menyederhanakan K-map.
Ikuti ini rules for simplifying K-maps untuk mendapatkan jumlah standar dari bentuk produk.
Pilih masing-masing K-map berdasarkan jumlah variabel yang ada dalam fungsi Boolean.
Jika fungsi Boolean diberikan sebagai penjumlahan dari bentuk suku min, letakkan salah satu di sel suku min masing-masing di K-map. Jika fungsi Boolean diberikan sebagai bentuk penjumlahan produk, maka tempatkan satu di semua kemungkinan sel K-map yang istilah produknya valid.
Periksa kemungkinan pengelompokan jumlah maksimum yang berdekatan. Ini harus menjadi kekuatan dua. Mulai dari daya tertinggi dua dan hingga daya terkecil dua. Pangkat tertinggi sama dengan jumlah variabel yang dipertimbangkan dalam K-map dan daya terkecil adalah nol.
Setiap pengelompokan akan menghasilkan istilah produk atau literal. Ini dikenal sebagaiprime implicant. Implikasi utama dikatakanessential prime implicant, jika setidaknya satu '1' tidak tercakup dalam pengelompokan lain tetapi hanya sampul pengelompokan tersebut.
Catat semua implikasi utama dan implikasi utama esensial. Fungsi Boolean yang disederhanakan berisi semua implikasi utama yang penting dan hanya implan utama yang diperlukan.
Note 1 - Jika keluaran tidak ditentukan untuk beberapa kombinasi masukan, maka nilai keluaran tersebut akan diwakili dengan don’t care symbol ‘x’. Artinya, kita dapat menganggapnya sebagai '0' atau '1'.
Note 2- Jika istilah tidak peduli juga ada, maka tempatkan tidak peduli 'x' di sel masing-masing K-map. Pertimbangkan hanya 'x' yang tidak peduli yang berguna untuk mengelompokkan jumlah maksimum yang berdekatan. Dalam kasus tersebut, perlakukan nilai tidak peduli sebagai '1'.
Contoh
Biarkan kami simplify fungsi Boolean berikut, f(W, X, Y, Z)= WX’Y’ + WY + W’YZ’ menggunakan K-map.
Fungsi Boolean yang diberikan adalah dalam bentuk penjumlahan produk. Ini memiliki 4 variabel W, X, Y & Z. Jadi, kami membutuhkan4 variable K-map. Itu4 variable K-map dengan yang sesuai dengan istilah produk yang diberikan ditunjukkan pada gambar berikut.
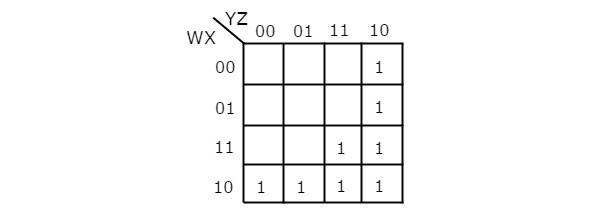
Di sini, 1s ditempatkan di sel K-map berikut.
Sel-sel yang sama dengan perpotongan Baris 4 dan kolom 1 & 2 berhubungan dengan istilah hasil kali, WX’Y’.
Sel, yang sama dengan perpotongan Baris 3 & 4 dan kolom 3 & 4 sesuai dengan istilah hasil kali, WY.
Sel-sel, yang sama dengan perpotongan Baris 1 & 2 dan kolom 4 sesuai dengan istilah hasil kali, W’YZ’.
Tidak ada kemungkinan pengelompokan baik 16 yang berdekatan atau 8 yang berdekatan. Ada tiga kemungkinan pengelompokan 4 yang berdekatan. Setelah ketiga pengelompokan ini, tidak ada satu pun yang tersisa sebagai tidak dikelompokkan. Jadi, kita tidak perlu memeriksa pengelompokan 2 yang berdekatan. Itu4 variable K-map dengan ketiganya groupings ditunjukkan pada gambar berikut.

Di sini, kami mendapat tiga implan utama WX ', WY & YZ'. Semua implikasi utama iniessential karena alasan berikut.
Dua orang (m8 & m9)pengelompokan baris keempat tidak tercakup dalam pengelompokan lain. Hanya pengelompokan baris keempat yang mencakup kedua pengelompokan tersebut.
Lajang (m15)pengelompokan bentuk persegi tidak tercakup oleh pengelompokan lain. Hanya pengelompokan bentuk persegi yang mencakup yang satu itu.
Dua orang (m2 & m6)pengelompokan kolom keempat tidak tercakup dalam pengelompokan lain. Hanya pengelompokan kolom keempat yang mencakup kedua kolom tersebut.
Oleh karena itu, simplified Boolean function adalah
f = WX’ + WY + YZ’
Ikuti ini rules for simplifying K-maps untuk mendapatkan produk standar dari bentuk penjumlahan.
Pilih masing-masing K-map berdasarkan jumlah variabel yang ada dalam fungsi Boolean.
Jika fungsi Boolean diberikan sebagai hasil kali dari bentuk istilah Max, maka letakkan nol di masing-masing sel istilah Max di K-map. Jika fungsi Boolean diberikan sebagai hasil perkalian dari bentuk penjumlahan, maka letakkan nol di semua kemungkinan sel K-map yang syarat penjumlahannya valid.
Periksa kemungkinan pengelompokan jumlah maksimum nol yang berdekatan. Ini harus menjadi kekuatan dua. Mulai dari daya tertinggi dua dan hingga daya terkecil dua. Pangkat tertinggi sama dengan jumlah variabel yang dipertimbangkan dalam K-map dan daya terkecil adalah nol.
Setiap pengelompokan akan menghasilkan istilah literal atau satu penjumlahan. Ini dikenal sebagaiprime implicant. Implikasi utama dikatakanessential prime implicant, jika setidaknya satu '0' tidak tercakup dalam pengelompokan lain tetapi hanya penutup pengelompokan tersebut.
Catat semua implikasi utama dan implikasi utama esensial. Fungsi Boolean yang disederhanakan berisi semua implikasi utama yang penting dan hanya implan utama yang diperlukan.
Note- Jika istilah tidak peduli juga ada, maka tempatkan tidak peduli 'x' di sel masing-masing K-map. Pertimbangkan hanya 'x' yang tidak peduli yang berguna untuk mengelompokkan jumlah maksimum nol yang berdekatan. Dalam kasus tersebut, perlakukan nilai tidak peduli sebagai '0'.
Contoh
Biarkan kami simplify fungsi Boolean berikut, $ f \ left (X, Y, Z \ right) = \ prod M \ left (0,1,2,4 \ kanan) $ menggunakan K-map.
Fungsi Boolean yang diberikan adalah hasil perkalian dari bentuk istilah Max. Ini memiliki 3 variabel X, Y & Z. Jadi, kita membutuhkan 3 variabel K-map. Suku Max yang diberikan adalah M 0 , M 1 , M 2 & M 4 . 3variable K-map dengan angka nol yang sesuai dengan suku Max yang diberikan ditunjukkan pada gambar berikut.

Tidak ada kemungkinan untuk mengelompokkan 8 angka nol yang berdekatan atau 4 angka nol yang berdekatan. Ada tiga kemungkinan untuk mengelompokkan 2 angka nol yang berdekatan. Setelah ketiga pengelompokan ini, tidak ada satu nol pun yang tersisa sebagai tidak dikelompokkan. Itu3 variable K-map dengan ketiganya groupings ditunjukkan pada gambar berikut.

Di sini, kita mendapat tiga implan utama X + Y, Y + Z & Z + X. Semua implikasi utama ini adalah essential karena satu nol di setiap pengelompokan tidak tercakup oleh pengelompokan lain kecuali dengan pengelompokan individualnya.
Oleh karena itu, simplified Boolean function adalah
f = (X + Y).(Y + Z).(Z + X)
Dengan cara ini, kita dapat dengan mudah menyederhanakan fungsi Boolean hingga 5 variabel menggunakan metode K-map. Untuk lebih dari 5 variabel, sulit untuk menyederhanakan fungsi menggunakan K-Maps. Sebab, banyaknyacells di K-map dapatkan doubled dengan memasukkan variabel baru.
Karena pemeriksaan dan pengelompokan yang berdekatan (istilah min) atau nol yang berdekatan (istilah Max) akan menjadi rumit. Kami akan membahasTabular method pada bab selanjutnya untuk mengatasi kesulitan metode K-map.