Sirkuit Digital - Logika Ambang Batas
Di bab-bab sebelumnya, kami telah mengimplementasikan berbagai rangkaian kombinasional menggunakan gerbang logika. Kecuali gerbang NOT, semua gerbang logika yang tersisa memiliki setidaknya dua input dan output tunggal. Demikian pula denganthreshold gate juga berisi setidaknya satu masukan dan hanya satu keluaran.
Selain itu, ini berisi bobot masing-masing untuk setiap masukan dan nilai ambang batas. Nilai bobot dan ambang batas ini dapat berupa bilangan riil berapapun.
Dasar-dasar gerbang Threshold
Misalkan input gerbang ambang adalah X 1 , X 2 , X 3 ,…, X n . Bobot yang sesuai dari input ini adalah W 1 , W 2 , W 3 ,…, W n . Itusymbol dari gerbang Threshold ditunjukkan pada gambar berikut.
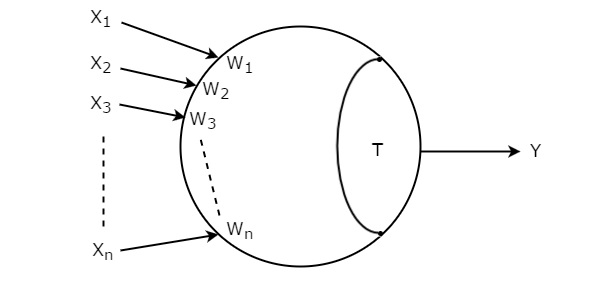
Threshold gatedirepresentasikan dengan lingkaran dan memiliki masukan 'n', X 1 hingga X n dan keluaran tunggal, Y. Lingkaran ini dibuat menjadi dua bagian. Satu bagian mewakili bobot yang sesuai dengan masukan dan bagian lainnya mewakili nilai Ambang, T.
Jumlah produk input dengan bobot yang sesuai dikenal sebagai weighted sum. Jika jumlah bobot ini lebih besar dari atau sama dengan nilai Ambang, T maka hanya keluarannya, Y akan sama dengan satu. Jika tidak, output, Y akan sama dengan nol.
Mathematically, kita dapat menulis hubungan antara input dan output dari gerbang Threshold seperti di bawah ini.
$$ Y = 1, jika \: \: W_ {1} X_ {1} + W_ {2} X_ {2} + W_ {3} X_ {3} + ... W_ {n} X_ {n} \ geq T $$
= 0, jika tidak.
Oleh karena itu, kita dapat mengimplementasikan berbagai gerbang logika dan fungsi Boolean hanya dengan mengubah nilai bobot dan / atau nilai Threshold, T.
Contoh
Mari kita temukan simplified Boolean function untuk gerbang Threshold berikut.

Gerbang Ambang ini memiliki tiga masukan X 1 , X 2 , X 3 dan satu keluaran Y.
Bobot yang sesuai dengan input X 1 , X 2 & X 3 masing-masing adalah W 1 = 2, W 2 = 1 & W 3 = -4.
Nilai gerbang Threshold adalah T = -1.
Itu weighted sum dari gerbang Threshold adalah
$$ W = W_ {1} X_ {1} + W_ {2} X_ {2} + W_ {3} X_ {3} $$
Gantikan bobot yang diberikan dalam persamaan di atas.
$$ \ Panah Kanan W = 2X_ {1} + X_ {2} -4X_ {3} $$
Output dari gerbang Threshold, Y akan menjadi '1' jika W ≥ −1, jika tidak maka akan menjadi '0'.
Pengikut table menunjukkan hubungan antara masukan dan keluaran untuk semua kemungkinan kombinasi masukan.
| Masukan | Jumlah tertimbang | Keluaran | ||
|---|---|---|---|---|
| $ X_ {1} $ | $ X_ {2} $ | $ X_ {3} $ | $ W = 2X_ {1} + X_ {2} -4X_ {3} $ | $ Y $ |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | -4 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | -3 | 0 |
| 1 | 0 | 0 | 2 | 1 |
| 1 | 0 | 1 | -2 | 0 |
| 1 | 1 | 0 | 3 | 1 |
| 1 | 1 | 1 | -1 | 1 |
Dari tabel di atas, kita dapat menulis Boolean function untuk keluaran, Y sebagai
$$ Y = \ jumlah m \ kiri (0,2,4,6,7 \ kanan) $$
Penyederhanaan fungsi Boolean ini menggunakan 3 variable K-Map ditunjukkan pada gambar berikut.

Oleh karena itu, simplified Boolean function untuk gerbang Ambang yang diberikan adalah $ Y = {X_ {3} '} + X_ {1} X_ {2} $.
Sintesis Fungsi Ambang
Gerbang ambang juga disebut sebagai universal gatekarena kita dapat mengimplementasikan fungsi Boolean menggunakan gerbang Threshold (s). Kadang-kadang, tidak mungkin untuk mengimplementasikan beberapa gerbang logika dan fungsi Boolean dengan menggunakan gerbang Threshold tunggal. Dalam hal ini, kami mungkin memerlukan beberapa gerbang Ambang.
Ikuti ini steps untuk mengimplementasikan fungsi Boolean menggunakan gerbang Threshold tunggal.
Step 1 - Merumuskan a Truth table untuk fungsi Boolean yang diberikan.
Step 2 - Dalam tabel Kebenaran di atas, tambahkan (sertakan) satu kolom lagi, yang memberikan hubungan antara weighted sums dan Threshold value.
Step 3 - Tuliskan hubungan antara jumlah tertimbang dan ambang batas untuk setiap kombinasi input seperti yang disebutkan di bawah ini.
Jika keluaran dari fungsi Boolean adalah 1, maka jumlah bobot akan lebih besar dari atau sama dengan nilai Ambang untuk kombinasi masukan tersebut.
Jika keluaran dari fungsi Boolean adalah 0, maka jumlah bobot akan lebih kecil dari nilai Ambang untuk kombinasi masukan tersebut.
Step 4 - Pilih nilai bobot & Ambang sedemikian rupa sehingga harus memenuhi semua relasi yang ada di kolom terakhir tabel di atas.
step 5 - Gambarlah symbol gerbang Threshold dengan bobot dan nilai Threshold tersebut.
Contoh
Mari kita terapkan berikut ini Boolean function menggunakan gerbang Threshold tunggal.
$$ Y \ kiri (X_ {1}, X_ {2}, X_ {3} \ kanan) = \ jumlah m \ kiri (0,2,4,6,7 \ kanan) $$
Fungsi Boolean yang diberikan adalah fungsi tiga variabel, yang direpresentasikan dalam bentuk jumlah min. ItuTruth table fungsi ini ditunjukkan di bawah.
| Masukan | Keluaran | ||
|---|---|---|---|
| X1 | X2 | X3 | Y |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Sekarang, mari kita tambahkan (sertakan) satu kolom lagi ke tabel Kebenaran di atas. Kolom terakhir ini berisi hubungan antaraweighted sums (W) and Threshold nilai (T) untuk setiap kombinasi input.
| Masukan | Keluaran | Hubungan antara W & T | ||
|---|---|---|---|---|
| X1 | X2 | X3 | Y | |
| 0 | 0 | 0 | 1 | 0 ≥T |
| 0 | 0 | 1 | 0 | W 3 <T |
| 0 | 1 | 0 | 1 | W 2 ≥ T |
| 0 | 1 | 1 | 0 | W 2 + W 3 <T |
| 1 | 0 | 0 | 1 | W 1 ≥ T |
| 1 | 0 | 1 | 0 | W 1 + W 3 <T |
| 1 | 1 | 0 | 1 | W 1 + W 2 ≥ T |
| 1 | 1 | 1 | 1 | W 1 + W 2 + W 3 ≥ T |
Berikut kesimpulan dari tabel di atas.
Nilai Ambang harus nol atau negatif berdasarkan relasi pertama.
Nilai W 3 harus negatif berdasarkan hubungan pertama dan kedua.
Nilai W 1 dan W 2 harus lebih besar dari atau sama dengan nilai Threshold berdasarkan relasi kelima dan ketiga.
W 2 harus lebih besar dari W 3 berdasarkan relasi keempat.
Kita dapat memilih nilai bobot dan Ambang berikut berdasarkan kesimpulan di atas.
W 1 = 2, W 2 = 1, W 3 = -4 & T = -1
Itu symbol dari gerbang Threshold dengan nilai di atas ditunjukkan di bawah ini.

Oleh karena itu, gerbang Ambang ini mengimplementasikan yang diberikan Boolean function, $ Y \ kiri (X_ {1}, X_ {2}, X_ {3} \ kanan) = \ jumlah m \ kiri (0,2,4,6,7 \ kanan) $.