Modellazione della divisione di un numero intero per una frazione
Qui, in questa lezione, impariamo come utilizzare il modello dell'area per dividere un numero intero per una frazione. C'è un numero intero e una frazione che divide quel numero intero. Consideriamo un numero intero come tanti quadrati come indica il numero Dividiamo ciascuno dei quadrati in tante parti come indica il denominatore della frazione. Troviamo il risultato di questa divisione contando il numero totale di parti dei quadrati.
Example:
Dividi 3 ÷ $ \ frac {1} {2} $ utilizzando un modello di area.
Solution
Step 1:
L'intero numero 3 è preso come tre quadrati. Poiché la frazione è la metà, ciascuno dei quadrati è diviso in due metà.
Step 2:
Ora le metà in tutti e tre i quadrati vengono contate e risulta essere 6. Questa è la risposta che otteniamo dividendo 3 per $ \ frac {1} {2} $ .
Quindi, 3 ÷ $ \ frac {1} {2} $ = 6
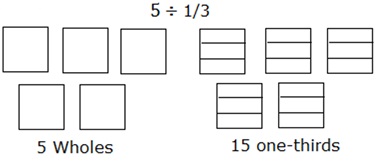
Dividi 5 ÷ $ \ frac {1} {3} $ utilizzando un modello di area.
Soluzione
Step 1:
Dividendo 5 in un terzo può essere modellato come segue:
Considera 5 quadrati come 5 interi. Ciascuno dei quadrati è ulteriormente diviso in tre parti o un terzo.
Step 2:
Quindi contando il numero totale di tali parti dei quadrati o degli interi si ottiene la risposta che è 15.
Quindi, 5 ÷ $ \ frac {1} {3} $ = 15
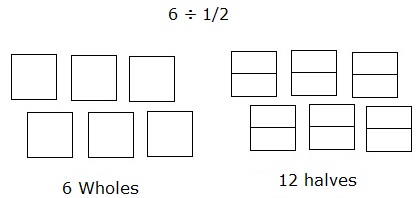
Dividi 6 ÷ $ \ frac {1} {2} $ utilizzando un modello di area.
Soluzione
Step 1:
La divisione di 6 in una metà può essere modellata come segue:
Considera 6 quadrati come 6 interi. Ciascuno dei quadrati è ulteriormente diviso in due parti o una metà.
Step 2:
Quindi contando il numero totale di tali parti dei quadrati o degli interi si ottiene la risposta che è 12.
Quindi, 6 ÷ $ \ frac {1} {2} $ = 12