宇宙論-クイックガイド
Cosmology宇宙の研究です。当時をさかのぼると、宇宙の起源についていくつかの考え方がありました。多くの学者はSteady State Theory。この理論によると、宇宙は常に同じであり、始まりはありませんでした。
信仰を持っていた人々のグループがあった間 Big Bang Theory。この理論は宇宙の始まりを予測します。再びモデルを支持するビッグバンからの熱い取り残された放射の証拠がありました。ビッグバン理論は、宇宙の軽い元素の存在量を予測します。したがって、ビッグバンの有名なモデルに従って、私たちは宇宙が始まりを持っていたと言うことができます。私たちは膨張する宇宙に住んでいます。
ハッブル赤方偏移
1900年代初頭、最先端の望遠鏡、 Mt Wilson、100インチの望遠鏡は当時最大の望遠鏡でした。ハッブルはその望遠鏡で働いた著名な科学者の一人でした。彼は天の川の外に銀河があることを発見しました。Extragalactic Astronomyたった100歳です。ウィルソン山は、200インチの望遠鏡を備えたパーマー天文台が建設されるまで最大の望遠鏡でした。
Hubble天の川の外で銀河を観測しているのはヒューメイソンだけではありませんでした。ヒューメイソンは彼を助けました。彼らは近くの銀河のスペクトルの測定に着手しました。次に彼らは、銀河スペクトルが連続発光で可視波長範囲にあることを観察しました。連続体の上に輝線と吸収線がありました。これらの線から、銀河が私たちから遠ざかっているのか、私たちに向かっているのかを推定することができます。
スペクトルを取得するとき、最も強い線はから来ていると仮定します H-α。文献から、最強の線はで発生するはずです6563 Å、しかし、線がどこかに発生する場合 7000Å、赤方偏移していると簡単に言えます。
から Special Theory of Relativity,
$$ 1 + z = \ sqrt {\ frac {1+ \ frac {v} {c}} {1- \ frac {v} {c}}} $$
ここで、Zは赤方偏移、無次元数、vは後退速度です。
$$ \ frac {\ lambda_ {obs}} {\ lambda_ {rest}} = 1 + z $$
ハッブルとヒューメイソンがリストアップ 22 Galaxies彼らの論文で。これらの銀河のほぼすべてが赤方偏移を示しました。彼らは速度(km / s)対距離(Mpc)をプロットしました。彼らは線形傾向を観察し、ハッブルは彼の有名な法則を次のように提唱しました。
$$ v_r = H_o d $$
これは Hubble Redshift Distance Relationship。下付き文字r膨張が半径方向であることを示します。$ v_r $は後退速度ですが、$ H_o $はハッブルパラメーターです。d私たちから銀河までの距離です。彼らは、宇宙の膨張率が均一であれば、遠く離れた銀河が私たちからより速く後退すると結論付けました。
拡張
すべてが私たちから遠ざかっています。銀河は静止しておらず、常に膨張調和があります。ハッブルパラメータの単位はキロ秒-1 MPC -1。– 1 Mpcの距離を離れると、銀河は200 km /秒の速度で移動します。ハッブルパラメータは、膨張率を示します。ハッブルとヒューメイソンによると、$ H_o $の値は200kms / sec / Mpcです。
データは、すべての銀河が私たちから遠ざかっていることを示しました。したがって、私たちが宇宙の中心にいることは明らかです。しかし、ハッブルはこの間違いを犯しませんでした。彼によれば、私たちがどの銀河に住んでいても、他のすべての銀河が私たちから遠ざかっています。したがって、結論は、銀河間の空間が拡大し、宇宙の中心がないということです。
拡大は至る所で起こっています。ただし、拡大に反対する力がいくつかあります。化学結合、重力、その他の引力が物体をまとめています。以前は、すべてのオブジェクトが互いに接近していました。ビッグバンを衝動的な力と見なすと、これらのオブジェクトは互いに離れるように設定されます。
タイムスケール
ローカルスケールでは、キネマティクスは重力によって制御されます。元のハッブルの法則では、青方偏移を示した銀河がいくつかありました。これは、銀河の複合重力ポテンシャルによるものと考えられます。重力はハッブルの法則から物事を切り離しました。アンドロメダ銀河が近づいています。重力は物事を遅くしようとしています。当初、拡張は減速していましたが、現在は加速しています。
ありました Cosmic Jerkこのため。ハッブルパラメータに対していくつかの推定が行われました。それは90年にわたって500kms / sec / Mpcから69kms / sec / Mpcに進化しました。値の不一致は、距離の過小評価によるものでした。ザ・Cepheid Stars 距離キャリブレータとして使用されましたが、さまざまなタイプのケフェイド星があり、この事実はハッブルパラメータの推定には考慮されていません。
ハッブル時間
ハッブル定数は、宇宙の年齢の現実的な推定値を提供します。$ H_o $は、銀河が同じ速度で動いている場合、宇宙の年齢を示します。$ H_o $の逆数は、ハッブル時間を与えます。
$$ t_H = \ frac {1} {H_o} $$
$ H_oの現在価値を置き換える、t_H $ = 14十億年。膨張率は宇宙の始まりを通して一定でした。これが当てはまらない場合でも、$ H_o $は宇宙の年齢に有用な制限を与えます。一定の膨張率を仮定して、距離と時間の間にグラフをプロットすると、グラフの傾きは速度で与えられます。
この場合、ハッブル時間は実際の時間と同じです。しかし、宇宙が過去に速く拡大し、現在にゆっくりと拡大していた場合、ハッブル時間は宇宙の年齢の上限を与えます。以前は宇宙がゆっくりと膨張し、現在は加速している場合、ハッブル時間は宇宙の年齢の下限を示します。
$ t_H = t_ {age} $ −膨張率が一定の場合。
$ t_H> t_ {age} $ -宇宙が過去に速く拡大し、現在は遅く拡大した場合。
$ t_H <t_ {age} $ -宇宙が過去にゆっくりと拡大し、現在に速く拡大した場合。
別の銀河群から200Mpcにある10個の銀河群を考えてみましょう。局部銀河群内の運動学は重力によって支配されているため、星団内の銀河は宇宙が膨張していると決して結論付けません。
覚えておくべきポイント
宇宙論は、私たちの宇宙の過去、現在、未来の研究です。
私たちの宇宙は約140億年前のものです。
宇宙は絶えず拡大しています。
ハッブルパラメータは、宇宙の年齢の尺度です。
の現在値 Ho は69kms / sec / Mpcです。
非常に長い間、私たちの天の川の外に銀河が存在するとは誰も考えていませんでした。1924年、エドウィンハッブルは検出しましたCepheid’sアンドロメダ星雲で、それらの距離を推定しました。彼は、これらの「渦巻星雲」は実際には他の銀河であり、私たちの天の川の一部ではないと結論付けました。したがって、彼はM31(アンドロメダ銀河)が島の宇宙であることを確立しました。これがの誕生でしたExtragalactic Astronomy。
セファイドのショー periodic dip in their brightness。観測によると、脈動の周期と呼ばれる連続するディップ間の周期は、光度に関連しています。したがって、それらは距離インジケーターとして使用できます。太陽のような主系列星は静水圧平衡にあり、それらはコアで水素を燃焼します。水素が完全に燃焼した後、星は赤色巨星相に向かって移動し、平衡を取り戻そうとします。
セファイド星は、主系列星から赤色巨星に移行している主系列後の星です。
セファイドの分類
これらの脈動変光星には3つの広いクラスがあります-
Type-I Cepheids (または古典的なセファイド)-30-100日の期間。
Type-II Cepheids (またはW Virginis Stars)-1〜50日の期間。
RR Lyrae Stars −0。1〜1日の期間。
当時、ハッブルはこの変光星の分類に気づいていませんでした。そのため、ハッブル定数が過大評価されていたため、彼は私たちの宇宙の年齢が低いと推定しました。そのため、後退速度も過大評価されていました。セファイドでは、擾乱は、新しい平衡が達成されるまで、星の中心から半径方向外側に伝播します。
明るさと脈動周期の関係
ここで、脈動周期が長いほど明るさが増すという事実の物理的根拠を理解してみましょう。光度Lと質量Mの星を考えてみましょう。
私たちはそれを知っています-
$$ L \ propto M ^ \ alpha $$
ここで、低質量の星の場合、α= 3〜4です。
から Stefan Boltzmann Law、私たちはそれを知っています-
$$ L \ propto R ^ 2 T ^ 4 $$
場合 R は半径、$ c_s $は音速、次に脈動の周期 P −と書くことができます
$$ P = R / c_s $$
しかし、任意の媒体を通過する音速は、温度で次のように表すことができます。
$$ c_s = \ sqrt {\ frac {\ gamma P} {\ rho}} $$
ここに、 γ 等温の場合は1です。
理想気体の場合、P = nkT、ここでkは Boltzmann Constant。だから、私たちは書くことができます-
$$ P = \ frac {\ rho kT} {m} $$
ここで、$ \ rho $は密度であり、 m 陽子の質量です。
したがって、期間は次の式で与えられます。
$$ P \ cong \ frac {Rm ^ {\ frac {1} {2}}} {(kT)^ {{\ frac {1} {2}}}} $$
Virial Theorem 等質量の物体(星、銀河など)の安定した自己重力の球形分布の場合、総運動エネルギーは k オブジェクトのは、総重力ポテンシャルエネルギーのマイナス半分に等しい u、すなわち、
$$ u = -2k $$
ビリアル定理がこれらの変光星に当てはまると仮定しましょう。星の表面にある陽子を考えると、ビリアル定理から次のように言うことができます。
$$ \ frac {GMm} {R} = mv ^ 2 $$
マクスウェル分布から、
$$ v = \ sqrt {\ frac {3kT} {2}} $$
したがって、期間-
$$ P \ sim \ frac {RR ^ {\ frac {1} {2}}} {(GM)^ {\ frac {1} {2}}} $$
これは
$$ P \ propto \ frac {R ^ {\ frac {3} {2}}} {M ^ {\ frac {1} {2}}} $$
私たちはそれを知っています– $ M \ propto L ^ {1 / \ alpha} $
また、$ R \ propto L ^ {1/2} $
だから、 β > 0、最終的に取得– $ P \ propto L ^ \ beta $
覚えておくべきポイント
セファイド星は、主系列星から赤色巨星に移行している主系列後の星です。
セファイドには、脈動周期の降順で、タイプI、タイプII、RR-ライラエの3種類があります。
セファイドの脈動周期は、その明るさ(光度)に正比例します。
ハッブルの観測は、視線速度がシフトに関連しているという事実を利用しました Spectral Lines。ここでは、4つのケースを観察し、後退速度($ v_r $)と赤方偏移(z)の関係を見つけます。
ケース1:ソース移動の非相対論的ケース
この場合、vはcよりはるかに小さくなります。ソースは何らかの信号(音、光など)を放出しており、次のように伝搬しています。Wavefronts。ソースフレームで2つの連続する信号を送信する間の時間間隔は次のとおりです。Δts。オブザーバーフレームで2つの連続する信号を受信する間の時間間隔は次のとおりです。Δto。

オブザーバーとソースの両方が静止している場合、Δts=Δtoですが、ここではそうではありません。代わりに、関係は次のとおりです。
$$ \ Delta t_o = \ Delta t_s + \ frac {\ Delta l} {c} $$
ここで、$ \ Delta l = v \ Delta t_s $
また、(波の速度×時間)=波長なので、次のようになります。
$$ \ frac {\ Delta t_o} {\ Delta t_s} = \ frac {\ lambda_o} {\ lambda_s} $$
上記の式から、次の関係が得られます。
$$ \ frac {\ lambda_o} {\ lambda_s} = 1 + \ frac {v} {c} $$
ここで、$ \ lambda _s $はソースでの信号の波長であり、$ \ lambda _o $はオブザーバーによって解釈された信号の波長です。
ここでは、ソースがオブザーバーから遠ざかっているので、 v ポジティブです。
赤方偏移−
$$ z = \ frac {\ lambda_o- \ lambda_s} {\ lambda_s} = \ frac {\ lambda_o} {\ lambda_s} -1 $$
上記の式から、次のように赤方偏移が得られます。
$$ z = \ frac {v} {c} $$
ケース2:オブザーバー移動の非相対論的ケース
この場合、vはcよりはるかに小さくなります。ここでは、$ \ Delta l $が異なります。
$$ \ Delta l = v \ Delta t_o $$

単純化すると、次のようになります。
$$ \ frac {\ Delta t_o} {\ Delta t_s} = \ left(1- \ frac {v} {c} \ right)^ {-1} $$
次のように赤方偏移が得られます-
$$ z = \ frac {v / c} {1-v / c} $$
以来 v << c、ケースIとケースIIの両方の赤方偏移式はほぼ同じです。
上記の2つのケースで得られた赤のシフトがどのように異なるかを見てみましょう。
$$ z_ {II} -z_I = \ frac {v} {c} \ left [\ frac {1} {1-v / c} -1 \ right] $$
したがって、$(v / c)^ 2 $係数のため、$ z_ {II} − z_ {I} $は非常に小さい数です。
これは、v << cの場合、ソースが移動しているか、オブザーバーが移動しているかを判断できないことを意味します。
理解しましょう Basics of STR (特殊相対性理論)−
光の速度は一定です。
光源(または観測者)が光速に匹敵する速度で移動している場合、相対論的効果が観察されます。
時間の遅れ:$ \ Delta t_o = \ gamma \ Delta t_s $
長さの収縮:$ \ Delta l_o = \ Delta t_s / \ gamma $
ここで、$ \ gamma $は Lorrentz factor、1より大きい。
$$ \ gamma = \ frac {1} {\ sqrt {1-(v ^ 2 / c ^ 2)}} $$
ケース3:ソース移動の相対論的ケース
この場合、vはcに相当します。ケースIと同じ図を参照してください。相対論的効果により、時間の遅れが観察され、次の関係が得られます。(ソースは相対論的な速度で動いています)
$$ \ Delta t_o = \ gamma \ Delta t_s + \ frac {\ Delta l} {c} $$
$$ \ Delta l = \ frac {v \ gamma \ Delta t_s} {c} $$
$$ \ frac {\ Delta t_o} {\ Delta t_s} = \ frac {1 + v / c} {\ sqrt {1-(v ^ 2 / c ^ 2)}} $$
さらに単純化すると、次のようになります。
$$ 1 + z = \ sqrt {\ frac {1 + v / c} {1-v / c}} $$
上記の式は、 Kinematic Doppler Shift Expression。
ケース4:オブザーバー移動の相対論的ケース
ケースIIと同じ図を参照してください。相対論的効果により、時間の短縮が見られ、以下の関係が得られます。(観測者は相対論的な速度で動いています)
$$ \ Delta t_o = \ frac {\ Delta t_s} {\ gamma} + \ frac {\ Delta l} {c} $$
$$ \ Delta l = \ frac {v \ Delta t_o} {c} $$
$$ \ frac {\ Delta t_o} {\ Delta t_s} = \ frac {\ sqrt {1-(v ^ 2 / c ^ 2)}} {1-v / c} $$
さらに単純化すると、次のようになります。
$$ 1 + z = \ sqrt {\ frac {1+ v / c} {1- v / c}} $$
上記の式は、ケースIIIで得られたものと同じです。
覚えておくべきポイント
後退速度と星の赤方偏移は関連する量です。
非相対論的ケースでは、ソースが移動しているか静止しているかを判断できません。
相対論的なケースでは、ソースまたはオブザーバーが移動する場合の赤方偏移と後退速度の関係に違いはありません。
動く時計はゆっくり動く、相対性理論の直接の結果です。
赤方偏移にある銀河 z = 10、 に対応 v≈80% の c。天の川の質量は周りにあります1011M⊙、暗黒物質を考えると、 1012M⊙。したがって、私たちの天の川は巨大です。の80%で動く場合c、オブジェクトの移動方法の一般的な概念には適合しません。
私たちは知っています、
$$ \ frac {v_r} {c} = \ frac {\ lambda_ {obs}-\ lambda {rest}} {\ lambda_ {rest}} $$
zの値が小さい場合、
$$ z = \ frac {v_r} {c} = \ frac {\ lambda_ {obs}-\ lambda_ {rest}} {\ lambda_ {rest}} $$
次のグラフ、つまりフラックスと波長の間のクラスでは、連続体の上に輝線があります。からH-α 行情報、私たちはそれを大まかに結論付けることができます z = 7。これは、銀河が70%で動いていることを意味しますc。私たちはシフトを観察し、それを速度として解釈しています。この概念を取り除き、z別の方法で。以下に示すように、宇宙を宇宙を表す2Dグリッドとして空間を想像してください。

黒い星は私たち自身の天の川であり、青い星は他の銀河であると考えてください。この銀河からの光を記録すると、スペクトルが見え、その赤方偏移、つまり銀河が遠ざかっていくことがわかります。光子が放出されたとき、それは相対速度を持っていました。
スペースが拡大している場合はどうなりますか?
これは、光子の瞬間的な赤方偏移です。2つの銀河の間の空間に沿った累積的な赤方偏移は、大きな赤方偏移になる傾向があります。やっと波長が変わります。それは銀河の運動学的な動きではなく、空間の拡大です。
次の画像は、相互重力が膨張をオーバーフローする場合、これはハッブルの法則に関与していないことを示しています。

キネマティックドップラーシフトでは、放出時に光子に赤方偏移が発生します。宇宙論的赤方偏移では、すべてのステップで、それは累積的に赤方偏移されています。重力ポテンシャルでは、光子は青方偏移します。重力ポテンシャルから這い出すと、赤方偏移します。
特殊相対性理論によると、互いに通過する2つのオブジェクトは、光速よりも大きい相対速度を持つことはできません。私たちが話す速度は宇宙の膨張です。zの値が大きい場合、赤方偏移は宇宙論的であり、私たちに対するオブジェクトの実際の後退速度の有効な測定値ではありません。
宇宙原理
それはから生じます Copernicus Notion宇宙の。この概念によると、宇宙は均質で等方性です。宇宙には好ましい方向と場所はありません。
均質性とは、宇宙のどの部分に住んでいても、宇宙がすべての部分で同じであることがわかることを意味します。等方性とは、どちらの方向を見ても同じ構造が見られることを意味します。
均質性の適切な例は水田です。全体的に均一に見えますが、風が吹くと向きにばらつきがあり、等方性ではありません。平らな土地にある山を考えてみましょう。山の頂上に観測者が立っています。彼は平らな土地の等方性を見るでしょうが、それは均質ではありません。均質な宇宙では、ある点で等方性である場合、どこでも等方性です。
宇宙をマッピングするための大規模な調査がありました。 Sloan Digital Sky Surveyこれはそのような調査の1つであり、赤緯ではなく赤経に焦点を当てています。ルックバック期間は約20億年です。すべてのピクセルは銀河の位置に対応し、色は形態学的構造に対応します。緑の色は青い渦巻銀河を表し、赤い偽色は巨大な銀河を表しています。
銀河は宇宙論的ウェブのフィラメント状の構造であり、銀河の間にボイドがあります。
$ \ delta M / M \ cong 1 $つまり、質量分布の変動は1 Mであり、特定の立方体内に存在する物質の質量です。この場合、ボリューム50Mpcキューブを取ります。
1000 Mpcの立方体側の場合、$ \ delta M / M \ cong 10 ^ {− 4} $。
均一性を定量化する1つの方法は、質量変動を取得することです。質量変動は、スケールが小さいほど大きくなります。
等方性を定量化するには、宇宙マイクロ波背景放射を検討してください。宇宙は大きな角度スケールでほぼ等方性です。
覚えておくべきポイント
互いに通過する2つのオブジェクトは、光速よりも大きい相対速度を持つことはできません。
宇宙原理は、宇宙は均質で等方性であると述べています。
この均一性は、非常に大きな角度スケールで存在し、小さなスケールでは存在しません。
SDSS(Sloan Digital Sky Survey)は、夜空をマッピングし、宇宙原理を検証するための取り組みです。
エネルギー保存の法則と質量保存の法則に従って、質量を含むエネルギーの総量(E = mc 2)は、宇宙のどのプロセスのすべてのステップでも変化しません。宇宙自体の膨張は、おそらく光子の波長の伸長(宇宙論的赤方偏移)、暗黒エネルギー相互作用などからのエネルギーを消費します。
26,000を超える銀河の調査をスピードアップするために、 Stephen A. Shectman112個の銀河を同時に測定できる機器を設計しました。金属板に、空の銀河の位置に対応する穴を開けました。光ファイバケーブルは、各銀河からの光を、2.5メートルのデュポン望遠鏡の分光器の別々のチャネルに運びました。Carnegie Observatories チリのセロラスカンパナスで。
最大の効率のために、として知られている特殊な技術 Drift-Scan Photometry望遠鏡が調査フィールドの始めに向けられ、次に自動運転がオフにされた、が使用されました。空が通り過ぎたとき、望遠鏡はじっと立っていた。コンピュータはから情報を読み取りますCCD Detector地球の自転と同じ速度で、一定の天体緯度で1つの長く連続した画像を生成します。測光の完了には合計450時間かかりました。
さまざまな形態のノイズが存在し、それらの数学的モデリングはその特性によって異なります。さまざまな物理的プロセスが、宇宙のパワースペクトルを大規模に進化させます。量子ゆらぎによって与えられる初期パワースペクトルは、周波数の負の3乗に従います。Pink Noise Spectrum 三次元で。
メトリック
宇宙論では、最初に空間の定義が必要です。メトリックは、空間内のポイントを表す数式です。空の観測は球面幾何学で行われます。したがって、球座標系を使用する必要があります。間隔の狭い2点間の距離は次の式で与えられます。
$$ ds ^ 2 = dr ^ 2 + r ^ 2 \ theta ^ 2 + r ^ 2 sin ^ 2 \ theta d \ phi ^ 2 $$
次の画像は、3次元の非拡張ユークリッド空間でのジオメトリを示しています。

この幾何学はまだ3次元の非拡張ユークリッド空間にあります。したがって、フレーム自体を定義する参照グリッドは拡張されます。次の画像は、増加したメトリックを示しています。

スケールファクターは、時間に対する宇宙の膨張を組み込んだ「スケールファクター」と呼ばれる非膨張空間の方程式に組み込まれます。
$$ ds ^ 2 = a ^ 2(t)\ left [dr ^ 2 + r ^ 2 \ theta ^ 2 + r ^ 2 sin ^ 2 \ theta d \ phi ^ 2 \ right] $$
どこ a(t) はスケールファクターであり、次のように記述されることもあります。 R(t)。一方、a(t) > 1 メートル法の倍率を意味しますが、 a(t) < 1 メトリックの縮小を意味し、 a(t) = 1一定のメトリックを意味します。慣例として、a(t0) = 1。
共動座標系
で Comoving Coordinate System, 測定スケールはフレームとともに膨張します(膨張宇宙)。
ここで、$ \ left [dr ^ 2 + r ^ 2 \ theta ^ 2 + r ^ 2 sin ^ 2 \ theta d \ phi ^ 2 \ right] $は共動距離であり、$ ds ^ 2 $は適切な距離。
適切な距離は、観測時に地球から離れた銀河で測定された実際の距離、つまり物体の瞬間距離に対応します。
これは、光子が遠方の光源から観測者に到達したときに移動した距離が、観測者の$ t = t_0 $で受信した距離になるためです。これは、瞬間的な観測距離が適切な距離になることを意味します。レート係数と最初に測定された長さを参照として使用して、将来の距離を予測します。
共動距離と適切な距離の概念は、観測された空間の特定の体積における銀河の数密度の実際の値を測定する上で重要です。共動距離を使用して、観測された光子が放出されたときの形成時の密度を計算する必要があります。これは、宇宙の膨張率を推定できれば得られます。
膨張率を推定するために、観測された遠方の銀河の距離の変化を長期間にわたって観測することができます。
覚えておくべきポイント
メトリックは、空間内のポイントを表す数式です。
スケールファクターは、宇宙が収縮しているか拡大しているかを決定します。
共動座標系では、測定スケールはフレームとともに拡大します(膨張宇宙)。
適切な距離は、オブジェクトの瞬間的な距離です。
共動距離は、オブジェクトの実際の距離です。
この章では、Robertson-Walkerメトリックについて詳しく説明します。
時間とともに変化するスケールファクターのモデル
遠方の銀河から光子が放出されたとしましょう。スペースはすべての方向のフォトンのために前方にあります。宇宙の膨張はあらゆる方向にあります。次の手順で、スケール係数が時間とともにどのように変化するかを見てみましょう。
Step 1 −静的宇宙の場合、スケール係数は1です。つまり、共動距離の値はオブジェクト間の距離です。
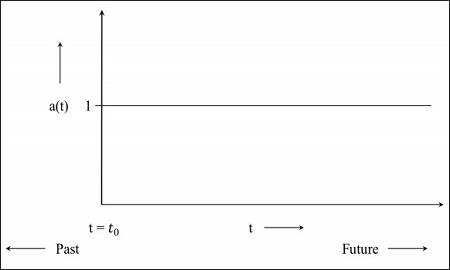
Step 2−次の画像は、まだ拡大しているが速度が減少している宇宙のグラフです。つまり、グラフは過去に開始されます。ザ・t = 0 宇宙がその時点から始まったことを示します。

Step 3 −次の画像は、より速い速度で拡大している宇宙のグラフです。

Step 4 −次の画像は、これから収縮し始める宇宙のグラフです。

スケールファクターの値が 0 宇宙の収縮の間に、それはオブジェクト間の距離が 0、つまり適切な距離は次のようになります 0。現在の宇宙の物体間の距離である共動距離は一定量です。将来、スケールファクターが0、すべてが近づきます。モデルは宇宙の構成要素に依存します。
平らな(ユークリッド:曲率のパラメーターはありません)膨張宇宙のメトリックは、次のように与えられます。
$$ ds ^ 2 = a ^ 2(t)\ left(dr ^ 2 + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2 \ right)$$
時空の場合、上記の式で得られた線要素は次のように変更されます。
$$ ds ^ 2 = c ^ 2dt ^ 2- \ left \ {a ^ 2(t)\ left(dr ^ 2 + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2 \右)\ right \} $$
時空の場合、光子が放出される時間と検出される時間は異なります。適切な距離は、宇宙の膨張によって時間とともに変化する可能性のあるオブジェクトまでの瞬間的な距離です。これは、フォトンがさまざまなオブジェクトから移動して私たちに到達した距離です。これは、共動距離に次のように関係しています。
$$ d_p = a(t)\ times d_c $$
ここで、$ d_p $は適切な距離であり、$ d_c $は固定されている共動距離です。
現在の宇宙の物体まで測定された距離は共動距離と見なされます。つまり、共動距離は固定されており、拡張によって変化しません。以前は、スケール係数は1未満でした。これは、適切な距離が小さかったことを示しています。
銀河への赤方偏移を測定することができます。したがって、適切な距離$ d_p $は$ c \ times t(z)$に対応します。ここで、$ t(z)$は赤方偏移へのルックバック時間であり、cは真空中の光速です。ルックバック時間は赤方偏移の関数です(z)。
上記の概念に基づいて、$ d_p = a(t)\ times d_c $のこのシナリオで宇宙論的赤方偏移がどのように解釈されるかを分析しましょう。
光子(地球に結合している)が銀河Gによって放出されたと仮定します。$ t_ {em} $は、光子が放出された時間に対応します。$ a(t_ {em})$は、フォトンが放出されたときのスケールファクターでした。光子の検出時までに、宇宙全体が拡大しました。つまり、光子は検出時に赤方偏移します。$ t_ {obs} $は、光子が検出された時間に対応し、対応するスケール係数は$ a(t_ {obs})$です。
宇宙が成長した要因は次の式で与えられます-
$$ \ frac {a(t_ {obs})} {a(t_ {em})} $$
波長が拡大した要因は−
$$ \ frac {\ lambda_ {obs}} {\ lambda_ {em}} $$
これは宇宙が成長した要因に等しいです。記号には通常の意味があります。したがって、
$$ \ frac {a(t_ {obs})} {a(t_ {em})} = \ frac {\ lambda_ {obs}} {\ lambda_ {em}} $$
私たちはその赤方偏移を知っています (z) は−
$$ z = \ frac {\ lambda_ {obs}-\ lambda_ {em}} {\ lambda_ {em}} = \ frac {\ lambda_ {obs}} {\ lambda_ {em}}-1 $$
$$ 1 + z = \ frac {a(t_ {obs})} {a(t_ {em})} $$
スケールファクターの現在の値は1であるため、$ a(t_ {obs})= 1 $であり、過去に$ a(t)$によってフォトンが放出されたときのスケールファクターを示します。
したがって、
$$ 1 + z = \ frac {1} {a(t)} $$
宇宙論における赤方偏移の解釈
これを理解するために、次の例を見てみましょう。$ z = 2 $の場合、$ a(t)= 1/3 $です。
これは、光がその物体を離れてから、宇宙が3倍に拡大したことを意味します。放射物体からの通過中に空間が同じ係数で拡大したため、受信した放射線の波長は3倍に拡大しました。このような大きな値では、z、赤方偏移は主に宇宙論的赤方偏移であり、私たちに対するオブジェクトの実際の後退速度の有効な尺度ではありません。
宇宙マイクロ波背景放射(CMB)の場合、 z = 1089、これは、現在の宇宙が次の係数で拡大したことを意味します ∼1090。平らなユークリッド膨張宇宙の計量は次のように与えられます-
$$ ds ^ 2 = a ^ 2(t)(dr ^ 2 + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2)$$
メトリックを任意の曲率で記述したいと思います。
Robertson and Walker 曲率ユニバース(均一で等方性)で証明された場合、メトリックは次のように与えられます。
$$ ds ^ 2 = a ^ 2(t)\ left [\ frac {dr ^ 2} {1-kr ^ 2} + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2 \ right] $$
これは一般的に知られています Robertson–Walker Metricそして、空間のあらゆるトポロジーに当てはまります。$ dr ^ 2 $の余分な要素に注意してください。ここに は曲率定数です。
宇宙の形
宇宙の形は、次の曲率の助けを借りて説明されています。
- 正の曲率
- 負の曲率
- 曲率ゼロ
これらのそれぞれを詳細に理解しましょう。
正の曲率
曲率のサーフェス上の任意のポイントで描画された接平面がサーフェス上のどのポイントでも交差しない場合、それは正の曲率を持つサーフェスと呼ばれます。つまり、サーフェスはそのポイントで接平面の片側に留まります。球の表面は正の曲率を持っています。
負の曲率
曲率の表面上の点に描かれた接平面が表面上の任意の点で交差する場合、それは負の曲率を持つ表面と呼ばれます。つまり、表面は2つの異なる方向に接平面から離れて湾曲します。鞍型の表面は負の曲率を持っています。
次に、球の表面について考えます。3点を測地線(大円の弧)で結合して球の表面に三角形を作成すると、球面三角形の内角の合計は180 oを超えます。つまり、−
$$ \ alpha + \ beta + \ gamma> \ pi $$
このような空間は、正に湾曲した空間と呼ばれます。また、曲率は均一で等方性です。一般に、球面三角形の頂点での角度は、次の関係に従います。
$$ \ alpha + \ beta + \ gamma = \ pi + A / R ^ 2 $$
どこ A は三角形の面積であり、 Rは球の半径です。次の画像は、正に湾曲した空間を示しています。

正の曲率の場合、平行線は一致する必要があります。正に湾曲した空間である地球の表面を考えてみましょう。赤道上の2つの開始点を取ります。赤道を直角に横切る線は経度線として知られています。これらの線は赤道と直角に交差するため、平行線と呼ぶことができます。赤道から始まり、最終的には極で交差します。この方法はによって使用されましたCarl Gauss と他の人は地球のトポロジーを理解します。
負考える-湾曲した空間(以下の図に示すサドル)を、内部の和は三角形の角度が180°未満であるOすなわち、 -
$$ \ alpha + \ beta + \ gamma <\ pi $$
頂点の角度は次の関係に従います-
$$ \ alpha + \ beta + \ gamma = \ pi-A / R ^ 2 $$

曲率ゼロ
平面の曲率はゼロです。ここで、平面空間の場合、平面を取り、測地線(直線)で3つの点を結合して三角形を作成すると、内部の角度の合計は次のようになります。
$$ \ alpha + \ beta + \ gamma = \ pi $$
次の画像は平らな2次元空間です。

空間を均一で等方性にしたい場合は、3つの可能性のみが残ります。空間を均一に平坦にするか、均一な正の曲率にするか、均一な負の曲率にするかです。
曲率定数は、次の3つの値のいずれかをとることができます。
$$ k = \ begin {cases} + 1、&for \:a \:positive \:curved \:space; \\\ quad 0、&for \:a \:flat \:space; \\-1 &for \:a \:負に\:湾曲\:スペース; \ end {cases} $$
宇宙のグローバルトポロジー
宇宙には特定のトポロジーがありますが、局所的にはしわがある可能性があります。物質が空間にどのように分布しているかに応じて、曲率の変化は小さくなります。宇宙のどこにいても同じ真のサイズを持つオブジェクトのクラスがあると仮定しましょう。つまり、それらは標準のキャンドルのようなものです。それらは同じ明るさではありませんが、同じサイズです。
オブジェクトが正に湾曲した空間にあり、光子が点A(オブジェクトの一方の端)とB(オブジェクトのもう一方の端)から来る場合、光子は測地線のパスを介して正に湾曲した空間で平行に伝播し、最終的に合流します。Cの観測者にとって、それは異なる方向の2つの異なる点から来たように見えます。
オブジェクトがローカルユニバースにあり、角度サイズを測定する場合、曲率の影響を受けません。同じクラスのオブジェクトがより大きな赤方偏移で見られる場合、角度サイズはと相関しません。
$$ \ theta = \ frac {d} {r} $$
どこ d オブジェクトのサイズであり、 rはオブジェクトまでの距離です。つまり、サイズがローカルサイズよりも大きい場合は、曲率が正であることを意味します。次の画像は、正に湾曲した空間で検出された光子を表したものです。

標準的なサイズと形態の実際の天体物理学的オブジェクトは存在しないことに注意してください。巨大な楕円形のcD–銀河は標準的なろうそくに合うと考えられていましたが、時間とともに進化していることもわかりました。
銀河までの距離を見つける
このセクションでは、次の画像を考慮して、銀河までの距離を見つける方法について説明します。

宇宙論的な休息フレームの(r、θ、)での天の川を考えてみましょう。= 0を取ることができます。(0、θ、ϕ)、つまり、均質性の仮定を呼び出すことによる宇宙の中心。
(r1、θ、)にある銀河「G」を考えてみましょう。距離(適切)は、光子が移動する最短の半径距離です。時空の対称性から、r = 0からr = r1までのヌル測地線は、空間内で一定の方向を持っています。その半径方向の伝搬では、角度座標は変化しません。角度座標が変更された場合、それは最短経路ではありません。これは、曲率項がDRに存在している理由である2。
覚えておくべきポイント
宇宙の膨張はあらゆる方向にあります。
宇宙は、スケールファクターの進化に応じて、静的、拡大、または縮小することができます。
cD銀河は時間とともに進化するため、標準光源として使用することはできません。
宇宙には特定のトポロジーがありますが、局所的にはしわがある可能性があります。
この章では、ハッブルパラメータとスケールファクターについて説明します。
Prerequisite −宇宙論的赤方偏移、宇宙原理。
Assumption −宇宙は均質で等方性です。
スケールファクターの変化率の割合を伴うハッブル定数
このセクションでは、ハッブル定数をスケールファクターの変化率と関連付けます。
速度は次のように記述して簡略化できます。
$$ v = \ frac {\ mathrm {d} r_p} {\ mathrm {d} t} $$
$$ = \ frac {d [a(t)r_c} {dt} $$
$$ v = \ frac {\ mathrm {d} a} {\ mathrm {d} t} \ ast \ frac {1} {a} \ ast(ar_c)$$
$$ v = \ frac {\ mathrm {d} a} {\ mathrm {d} t} \ ast \ frac {1} {a} \ ast r_p $$
ここに、 v は後退速度です。 a はスケールファクターであり、 rp 銀河間の適切な距離です。
Hubble’s Empirical Formula 性質のものだった-
$$ v = H \ ast r_p $$
したがって、上記の2つの方程式を比較すると、次のようになります。
Hubble’s Parameter = Fractional rate of change of the scale factor
$$ H = da / dt \ ast 1 / a $$
Note−スケール係数は時間の関数であるため、これは定数ではありません。したがって、それはハッブルの定数ではなく、ハッブルのパラメータと呼ばれます。
経験的に私たちは書く-
$$ H = V / D $$
したがって、この式から、 D 増加していて V は定数であり、 H 時間と宇宙の膨張とともに減少します。
ロバートソン-ウォーカーモデルと組み合わせたフリードマン方程式
このセクションでは、フリードマン方程式をロバートソン-ウォーカーモデルと組み合わせて使用する方法を理解します。これを理解するために、距離にテスト質量がある次の画像を撮りましょうrp 質量体から M 例として。

上の画像を考慮すると、力は次のように表すことができます。
$$ F = G \ ast M \ ast \ frac {m} {r ^ 2_p} $$
ここに、 G は万有引力定数であり、ρは観測可能な宇宙内の物質密度です。
ここで、球内の質量密度が均一であると仮定すると、次のように書くことができます。
$$ M = \ frac {4} {3} \ ast \ pi \ ast r_p ^ 3 \ ast \ rho $$
これらを力の方程式に戻すと、次のようになります。
$$ F = \ frac {4} {3} \ ast \ pi \ ast G \ ast r_p \ ast \ rho \ ast m $$
したがって、質量の位置エネルギーと運動エネルギーを書くことができます m として-
$$ V =-\ frac {4} {3} \ ast \ pi \ ast G \ ast r ^ 2_p \ ast m \ ast \ rho $$
$$ KE = \ frac {1} {2} \ ast m \ ast \ frac {\ mathrm {d} r_p ^ 2} {\ mathrm {d} t} $$
を使用して Virial Theorem −
$$ U = KE + V $$
$$ U = \ frac {1} {2} \ ast m \ ast \ left(\ frac {\ mathrm {d} r_p} {\ mathrm {d} t} \ right)^ 2- \ frac {4} { 3} \ ast \ pi \ ast G \ ast r_p ^ 2 \ ast m \ ast \ rho $$
しかし、ここでは、$ r_p = ar_c $です。したがって、次のようになります。
$$ U = \ frac {1} {2} \ ast m \ ast \ left(\ frac {\ mathrm {d} a} {\ mathrm {d} t} \ right)^ 2 r_c ^ 2- \ frac { 4} {3} \ ast \ pi \ ast G \ ast r_p ^ 2 \ ast m \ ast \ rho $$
さらに単純化すると、フリードマン方程式が得られます。
$$ \ left(\ frac {\ dot {a}} {a} \ right)^ 2 = \ frac {8 \ pi} {3} \ ast G \ ast \ rho + \ frac {2U} {m} \ ast r_c ^ 2 \ ast a ^ 2 $$
ここに Uは定数です。また、私たちが現在住んでいる宇宙は物質によって支配されていますが、放射線エネルギー密度は非常に低いことにも注意してください。
覚えておくべきポイント
ハッブルパラメータは、時間と宇宙の膨張とともに減少します。
私たちが現在住んでいる宇宙は物質に支配されており、放射線エネルギー密度は非常に低いです。
この章では、フリードマン方程式とは何かを理解し、さまざまな曲率定数のワールドモデルについて詳しく調べます。
フリードマン方程式
この方程式は、宇宙の均質で等方性のモデルにおける空間の膨張について教えてくれます。
$$ \ left(\ frac {\ dot {a}} {a} \ right)^ 2 = \ frac {8 \ pi G} {3} \ rho + \ frac {2U} {mr_c ^ 2a ^ 2} $ $
これは、 General Relativity (GR)およびRobertson-WalkerMetricは次のとおりです。
GR方程式の使用-
$$ \ frac {2U} {mr_c ^ 2} = -kc ^ 2 $$
どこ kは曲率定数です。したがって、
$$ \ left(\ frac {\ dot {a}} {a} \ right)^ 2 = \ frac {8 \ pi G} {3} \ rho- \ frac {kc ^ 2} {a ^ 2} $ $
また、$ \ rho $は、物質、放射線、その他の形式のエネルギーを含むエネルギー密度に置き換えられます。ただし、表現の目的で、$ \ rho $と表記されています。
さまざまな曲率定数のワールドモデル
ここで、曲率定数の値に応じてさまざまな可能性を見てみましょう。
ケース1:k = 1、または閉じた宇宙
膨張宇宙の場合、$ da / dt> 0 $。拡張が続くと、上記の式のRHSの最初の項は$ a ^ {-3} $になり、2番目の項は$ a ^ {-2} $になります。2つの項が等しくなると、宇宙は膨張を停止します。次に−
$$ \ frac {8 \ pi G} {3} \ rho = \ frac {kc ^ 2} {a ^ 2} $$
したがって、ここで、k = 1
$$ a = \ left [\ frac {3c ^ 2} {8 \ pi G \ rho} \ right] ^ {\ frac {1} {2}} $$
そのような宇宙は有限であり、有限体積を持っています。これはクローズドユニバースと呼ばれます。
ケース2:k = -1、またはオープンユニバース
場合 k < 0、拡張が停止することはありません。ある時点以降、RHSの第1項は、第2項と比較して無視できます。
ここで、k = -1です。したがって、$ da / dt〜c $。
この場合、宇宙は惰性で進んでいます。そのような宇宙には無限の空間と時間があります。これはオープンユニバースと呼ばれます。
ケース3:k = 0、またはフラットユニバース
この場合、宇宙は減少する速度で膨張しています。ここで、k = 0です。したがって、
$$ \ left(\ frac {\ dot {a}} {a} \ right)^ 2 = \ frac {8 \ pi G} {3} \ rho $$
そのような宇宙には無限の空間と時間があります。これはフラットユニバースと呼ばれます。
覚えておくべきポイント
フリードマン方程式は、宇宙の均質で等方性のモデルにおける空間の膨張について教えてくれます。
さまざまな曲率定数値に応じて、閉じたユニバース、開いたユニバース、またはフラットなユニバースを使用できます。
この章では、流体方程式と、それが時間とともに変化する宇宙の密度に関してどのようにわかるかについて説明します。
ρの推定C現在の宇宙で、ρを
現在の宇宙のために-
$$ \ rho_c \ simeq 10 ^ {11} M_ \ odot M_ {pc} ^ {-3} \ simeq 10 \:水素\:原子\:m ^ {-3} $$
私たちの宇宙空間には、あらゆる範囲の臨界密度があります。同様に、銀河間媒体の場合、$ \ rho_c $は1水素原子$ m ^ {-3} $ですが、分子雲の場合は$ 10 ^ 6 $水素原子$ m ^ {-3} $です。
空間の適切なサンプルを考慮して、$ \ rho_c $を測定する必要があります。私たちの銀河の中では、$ \ rho_c $の値は非常に高いですが、私たちの銀河は宇宙全体を代表するものではありません。ですから、宇宙原理が成り立つ宇宙、つまり距離≈300Mpcに出かける必要があります。300 Mpcを見るということは、10億年前を振り返ることを意味しますが、それは今でも現在の宇宙です。
SDSSのような調査は、実際の物質密度を決定するために実施されます。彼らは、5×500×5 MPC取る3ボリュームを、銀河の数をカウントし、これらの銀河から来るすべての光を追加します。1L≡1M、すなわち1太陽光度≡1太陽質量という仮定の下で。
光から質量への変換を行い、そのボリュームに存在する可視物質粒子に基づいてバリオンの数を推定しようとします。
例えば、
$$ 1000L_ \odot≡1000M_\ odot / m_p $$
ここで、m p =陽子の質量。
次に、おおよそバリオン数密度$ \ Omega b〜 = 0.025 $を取得します。これは、$ \ rho b = $ \ rho_c $の0.25%$を意味します。調査が異なれば、わずかに異なる値が得られます。したがって、局所宇宙では、可視物質の数密度は臨界密度よりはるかに低く、つまり私たちは開いた宇宙に住んでいます。
これらの調査は電磁放射を考慮しているが暗黒物質は考慮していないため、係数10の質量はこれらの調査には含まれていません。与える、$ \ Omega_m = 0.3 − 0.4 $。それでも、私たちは開かれた宇宙に住んでいると結論付けています。
暗黒物質は重力と相互作用します。暗黒物質が多いと膨張が止まることがあります。$ \ rho $が時間とともにどのように変化するかはまだ形式化されていないため、別の方程式のセットが必要です。
熱力学は次のように述べています-
$$ dQ = dU + dW $$
サイズの点で成長しているシステムの場合、$ dW = P dV $。宇宙の膨張は断熱としてモデル化されます。つまり、$ dQ = 0 $です。したがって、体積変化は内部エネルギーdUの変化から発生するはずです。
単位共動半径の宇宙の特定のボリューム、つまり$ r_c = 1 $を取りましょう。$ \ rho $がこの空間の体積内の材料の密度である場合、、
$$ M = \ frac {4} {3} \ pi a ^ 3r_c ^ 3 \ rho $$
$$ U = \ frac {4} {3} \ pi a ^ 3 \ rho c ^ 2 $$
どこ、 Uはエネルギー密度です。宇宙が膨張するにつれて、時間とともに内部エネルギーが変化することを調べてみましょう。
$$ \ frac {\ mathrm {d} U} {\ mathrm {d} t} = 4 \ pi a ^ 2 \ rho c ^ 2 \ frac {\ mathrm {d} a} {\ mathrm {d} t} + \ frac {4} {3} \ pi a ^ 3 c ^ 2 \ frac {\ mathrm {d} \ rho} {\ mathrm {d} t} $$
同様に、時間の経過に伴う体積の変化は、次の式で与えられます。
$$ \ frac {\ mathrm {d} V} {\ mathrm {d} t} = 4 \ pi a ^ 2 \ frac {\ mathrm {d} a} {\ mathrm {d} t} $$
$ dU = −P dV $を代入します。我々が得る、
$$ 4 \ pi a ^ 2(c ^ 2 \ rho + P)\ dot {a} + \ frac {4} {3} \ pi a ^ 3c ^ 2 \ dot {\ rho} = 0 $$
$$ \ dot {\ rho} +3 \ frac {\ dot {a}} {a} \ left(\ rho + \ frac {P} {c ^ 2} \ right)= 0 $$
これは、 Fluid Equation。宇宙の密度が時間とともにどのように変化するかを教えてくれます。
宇宙が膨張するにつれて圧力は低下します。すべての瞬間に圧力が変化しますが、考慮される体積の2点間に圧力差がないため、圧力勾配はゼロです。相対論的な材料だけが圧力を与え、物質は圧力がかかりません。
フリードマン方程式と流体方程式は宇宙をモデル化します。
覚えておくべきポイント
暗黒物質は重力と相互作用します。暗黒物質が多いと膨張が止まることがあります。
流体方程式は、宇宙の密度が時間とともにどのように変化するかを示しています。
フリードマン方程式と流体方程式は宇宙をモデル化します。
相対論的な材料だけが圧力を与え、物質は圧力がかかりません。
この章では、物質が支配する宇宙に関連するフリードマン方程式の解について説明します。宇宙論では、太陽系、銀河などすべてを大規模に見ているので、すべてがたまたま塵の粒子のように見えます(それが私たちの目で見ているものです)。それを塵の宇宙または物質のみの宇宙と呼ぶことができます。
の中に Fluid Equation、
$$ \ dot {\ rho} = -3 \ left(\ frac {\ dot {a}} {a} \ right)\ rho -3 \ left(\ frac {\ dot {a}} {a} \ right )\ left(\ frac {P} {c ^ 2} \ right)$$
圧力項があることがわかります。ほこりっぽい宇宙の場合、P = 0なぜなら、物質のエネルギー密度は放射圧よりも大きくなり、物質は相対論的な速度で動いていないからです。
したがって、流体方程式は次のようになります。
$$ \ dot {\ rho} = -3 \ left(\ frac {\ dot {a}} {a} \ right)\ rho $$
$$ \ Rightarrow \ dot {\ rho} a + 3 \ dot {a} \ rho = 0 $$
$$ \ Rightarrow \ frac {1} {a ^ 3} \ frac {\ mathrm {d}} {\ mathrm {d} t}(a ^ 3 \ rho)= 0 $$
$$ \ Rightarrow \ rho a ^ 3 = \:定数$$
$$ \ Rightarrow \ rho \ propto \ frac {1} {a ^ 3} $$
ボリュームが$ a ^ 3 $として増加しているため、密度は$ a ^ {-3} $としてスケーリングする必要があるため、この方程式には直感に反するものはありません。
最後の関係から、私たちはそれを言うことができます、
$$ \ frac {\ rho(t)} {\ rho_0} = \ left [\ frac {a_0} {a(t)} \ right] ^ 3 $$
現在の宇宙では、 a、これは a0 1である必要があります。
$$ \ rho(t)= \ frac {\ rho_0} {a ^ 3} $$
物質が支配する平らな宇宙では、k = 0です。したがって、フリードマン方程式は次のようになります。
$$ \ left(\ frac {\ dot {a}} {a} \ right)^ 2 = \ frac {8 \ pi G \ rho} {3} $$
$$ \ dot {a} ^ 2 = \ frac {8 \ pi G \ rho a ^ 2} {3} $$
この方程式を解くことにより、次のようになります。
$$ a \ propto t ^ {2/3} $$
$$ \ frac {a(t)} {a_0} = \ left(\ frac {t} {t_0} \ right)^ {2/3} $$
$$ a(t)= \ left(\ frac {t} {t_0} \ right)^ {2/3} $$
これは、宇宙が減少する速度で増加し続けることを意味します。次の画像は、ダスティユニバースの拡大を示しています。

ρは時間とともにどのように変化しますか?
次の方程式を見てください-
$$ \ frac {\ rho(t)} {\ rho_0} = \ left(\ frac {t_0} {t} \ right)^ 2 $$
スケールファクターは$ t ^ {2/3} $として時間とともに変化することがわかっています。そう、
$$ a(t)= \ left(\ frac {t} {t_0} \ right)^ {2/3} $$
それを差別化すると、私たちは得るでしょう、
$$ \ frac {(da)} {dt} = \ dot {a} = \ frac {2} {3} \ left(\ frac {t ^ {-1/3}} {t_0} \ right)$$
私たちは、 Hubble Constant は、
$$ H(t)= \ frac {\ dot {a}} {a} = \ frac {2} {3t} $$
これはの方程式です Einstein-de sitter Universe。宇宙の現在の年齢を計算したい場合は、
$$ t_0 = t_ {age} = \ frac {2} {3H_0} $$
現在の宇宙の$ H_0 $の値を入力すると、宇宙の年齢の値は次のようになります。 9 Gyrs。沢山ありますGlobular Cluster それ以上の年齢を持つ私たち自身の天の川銀河で。
それはすべてほこりっぽい宇宙についてでした。さて、宇宙が物質ではなく放射線によって支配されていると仮定すると、放射線エネルギー密度は$ a ^ {-3} $ではなく$ a ^ {-4} $になります。これについては、次の章で詳しく説明します。
覚えておくべきポイント
宇宙論では、すべてがたまたま塵の粒子のようであるため、私たちはそれを塵の宇宙または物質のみの宇宙と呼びます。
宇宙が物質ではなく放射線によって支配されていると仮定すると、放射線エネルギー密度は$ a ^ {-3} $ではなく$ a ^ {-4} $になります。
この章では、放射線が支配的な宇宙に関連するフリードマン方程式の解について説明します。最初に、物質のエネルギー密度を放射線のエネルギー密度と比較します。これにより、私たちの宇宙が物質に支配されているのか、放射線に支配されているのかを知ることができます。
放射線のエネルギー密度
現在の宇宙で蔓延している放射線は、恒星の源にほとんど起因することができませんが、それは主に残りのCMB(宇宙マイクロ波背景放射)によるものです。
放射線のエネルギー密度$ \ epsilon _ {\ gamma、0} $は、次のように表すことができます。
$$ \ epsilon _ {\ gamma、0} = aT_0 ^ 4 $$
ここに、 a は、式$(8 \ pi ^ 5k_B ^ 4)/(15h ^ 3c ^ 2)$が等しい放射定数です。 a = 7.5657 × 10−15erg\: cm−3 K−4。ここで考える温度T0は、CMBに対応する黒体の温度に対応します。
結果を代入すると、次のようになります。
$$ \ epsilon _ {\ gamma、0} = aT_0 ^ 4 = 4 \ times 10 ^ {-13} erg \:cm ^ {-3} $$
物質のエネルギー密度
以下の計算では、平らな宇宙とK = 0で作業することを前提としています。物質のエネルギー密度を$ \ epsilon = \ rho c ^ 2 $と見なします。次のことを考慮します-
$$ \ rho_ {m、0} c ^ 2 = 0.3 \ rho_ {c、0} c ^ 2 = 0.3 \ times \ frac {3H_0 ^ 2} {8 \ pi G} \ times c ^ 2 $$
$$ \ rho_ {m、0} c ^ 2 \ simeq 2 \ times 10 ^ {-8} erg \:cm ^ {-3} $$
$$ \ rho_ {b、0} c ^ 2 = 0.03 \ rho_ {c、0} c ^ 2 = 0.03 \ times \ frac {3H_0 ^ 2} {8 \ pi G} \ times c ^ 2 $$
$$ \ rho_ {b、0} c ^ 2 \ simeq 2 \ times 10 ^ {-9} erg \:cm ^ {-3} $$
したがって、上記の計算から、私たちは物質が支配する宇宙に住んでいることがわかります。これは、CMBが非常に冷たいという事実によってサポートすることができます。時間を振り返ると、CMBの温度が高くなり、宇宙が放射線に支配されていた時代があったのではないかと結論付けることができます。
密度とスケールファクターの変動
流体方程式は次のことを示しています。
$$ \ dot {\ rho} + 3 \ frac {\ dot {a}} {a} \ left(\ rho + \ frac {P} {c ^ 2} \ right)= 0 $$
ほこりっぽい宇宙を考えると、P = 0になります。前の結果は別として、宇宙は放射線によって支配されていると考えます。
$$ \ dot {\ rho} _ {rad} + 3 \ frac {\ dot {a}} {a} \ left(\ rho_ {rad} + \ frac {P} {c ^ 2} \ right)= 0 $$
$ P_ {rad} = \ rho c ^ {2/3} $の圧力関係を使用すると、次のようになります。
$$ \ dot {\ rho} _ {rad} + 3 \ frac {\ dot {a}} {a} \ left(\ rho_ {rad} + \ frac {\ rho_ {rad}} {3} \ right) = 0 $$
$$ \ dot {\ rho} _ {rad} + 4 \ frac {\ dot {a}} {a}(\ rho_ {rad})= 0 $$
さらに単純化すると、次のようになります。
$$ \ frac {1} {a ^ 4} \ frac {\ mathrm {d}} {\ mathrm {d} t}(\ rho_ {rad} a ^ 4)= 0 $$
$$ \ rho_ {rad} a ^ 4 = \:定数$$
$$ \ rho_ {rad} \ propto \ frac {1} {a ^ 4} $$
上記の結果は、$ \ rho $を使用したaの4乗の逆変動を示しています。
これは、ボリュームが増加するにつれて変化することから来る$ a ^ {-3} $として物理的に解釈できます。残りの$ a ^ {-1} $は、宇宙の空間の膨張によって光子によって失われたエネルギーとして扱うことができます(宇宙論的赤方偏移1 + z = a -1)。
次の画像は、物質と放射線密度の経時変化を示しています。
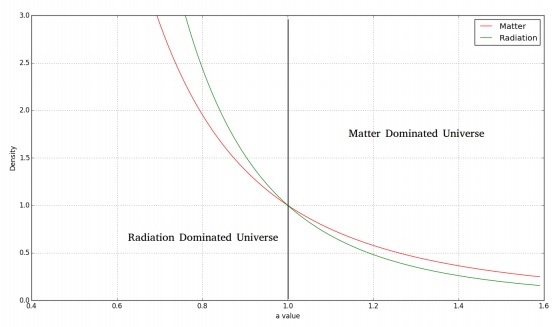
平らで放射線が支配的な宇宙の場合、フリードマン方程式は次のようになります。
$$ \ left(\ frac {\ dot {a}} {a} \ right)^ 2 = \ frac {8 \ pi G \ rho} {3} $$
$$ \ left(\ frac {\ dot {a}} {a} \ right)^ 2 = \ frac {8 \ pi G} {3} \ frac {\ rho_0} {a ^ 4} $$
単純化して解を微分方程式に適用すると、次のようになります。
$$(\ dot {a})^ 2 = \ frac {8 \ pi G \ rho_0} {3a ^ 2} $$
$$ \ Rightarrow a(t)\ propto t ^ {\ frac {1} {2}} $$
したがって、次のようになります。
$$ a(t)= a_0 \ left(\ frac {t} {t_0} \ right)^ {\ frac {1} {2}} $$
上記の式から、スケールファクターの増加率はほこりっぽい宇宙のそれよりも小さいことがわかります。
覚えておくべきポイント
現在の宇宙で流行している放射線は、恒星の源にほとんど起因することができません。
ほこりっぽい宇宙の場合、圧力はゼロです。
CMBはとても寒いです。
ダークエネルギーの領域は、すべての方程式の自由パラメーターであるため、天文学では非常に灰色の領域ですが、これが正確に何であるかは明確にわかりません。
フリードマン方程式から始めましょう。
$$ \ left(\ frac {\ dot {a}} {a} \ right)^ 2 = \ frac {8 \ pi G} {3} \ rho- \ frac {k \ ast c ^ 2} {a ^ 2} $$
宇宙論に関する基本的な本のほとんどは、ハッブルの観測の前に宇宙が閉じていて静止しているというこのエピソードからのダークエネルギーを説明することから始まります。
さて、宇宙が右側で静的であるためには、両方の項が一致し、それらがゼロである必要がありますが、最初の項が2番目の項よりも大きい場合、宇宙は静的ではないため、アインシュタインは自由パラメーターを削除しました ∧ 宇宙を静的にするためにフィールド方程式に入れて、彼は、最初の項が2番目の項と比較されても、方程式にもう1つの成分があれば、いつでも静的宇宙を得ることができると主張しました。これらの2つの用語を一致させます。
$$ \ left(\ frac {\ dot {a}} {a} \ right)^ 2 = \ frac {8 \ pi G} {3} \ rho- \ frac {k \ ast c ^ 2} {a ^ 2} + \ frac {\ wedge} {3} $$
$$ \ left(\ frac {\ ddot {a}} {a} \ right)=-\ frac {4 \ pi G} {3} \ left(\ rho + \ frac {3P} {c ^ 2} \右)+ \ frac {\ wedge} {3} $$
ここで、$ P = \ rho \ ast c ^ 2/3 $および$ \ wedge = \ rho \ ast c ^ 2 $は宇宙論的パラメーターです。(負の符号は魅力のためだけです)
上記の式(加速式)-
$ 3P / c ^ 2 $は、放射線による負圧です。
$ -4 \ pi G / 3 $は重力による引力であり、
$ \ wedge / 3 $は前向きな貢献をします。
方程式の別の部分が魅力的であるため、第3項は反発力として機能します。
方程式の物理的重要性は次のとおりです。 ˙a = 0宇宙が膨張していることを示す証拠がなかったからです。これらの2つの項が互いに一致しない場合はどうなるので、コンポーネントを追加することをお勧めします。オフセットに応じて、自由パラメーターの値をいつでも変更できます。
当時、この宇宙論的パラメーターについての物理的な説明はありませんでした。そのため、膨張宇宙の説明が1920年代に発見されたとき、 Einstein すぐにこの定数を捨てなければなりませんでした。
これの説明 cosmological constant 宇宙の異なるバージョンを説明しているため、まだ使用されていますが、この宇宙定数の定義、解釈の方法は時間とともに変化し続けました。
現在、この宇宙定数の概念は、多くの理由で宇宙論に戻されています。その理由の1つは、宇宙のさまざまな成分(バリオン、暗黒物質、放射線)のエネルギー密度を観測しているため、このパラメーターが何であるかがわかっていることです。を使用した独立した観測cosmic microwave background k = 0であることを示しています。
$$ CMB、k = 0 \:\ rho = \ rho_c = \ frac {3H_0 ^ 2} {8 \ pi G} \約10 \:水素\:atoms.m ^ {-3} $$
kが0であるためには、$ \ rho $は$ \ rho_c $と等しくなければなりませんが、それを合計すると0にならないことがわかっています。つまり、それがはるかに小さいことを示す他のコンポーネントがあることを意味します。 $ \ rho_c $。
$$ \ rho = \ rho_b + \ rho_ {DM} + \ rho_ {rad} << \ rho_c $$
ダークエネルギーのもう1つの証拠は、 Type 1 Supernova Observationこれは、白色矮星が物質を降着させ、チャンドラセカール限界(非常に正確な限界(約1.4M))を超えたときに発生します。これで、1型超新星爆発が発生するたびに、同じ質量になります。つまり、システムの総結合エネルギーは同じであり、見ることができる光エネルギーの量も同じです。
もちろん、超新星の光は増加してから弱まりますが、ピークの明るさを測定すると、常に同じになり、標準的な候補になります。したがって、タイプ1超新星では、宇宙の宇宙論的要素を測定するために使用しました。天文学者は、赤方偏移の大きい超新星は、赤方偏移の小さい超新星よりも30%〜40%暗いことを発見しました。 -ゼロ∧ 期間。
宇宙論モデルでは DE (Dark Energy)は流体として扱われます。つまり、状態方程式を書くことができます。状態方程式は、物質の2つの異なる状態の圧力、密度、温度、体積などの変数を接続する方程式です。
次元的には、
$$ \ frac {8 \ pi G} {3} \ rho = \ frac {\ wedge} {3} $$
$$ \ rho_ \ wedge = \ frac {\ wedge} {8 \ pi G} $$
DEのエネルギー密度、
$$ \ epsilon_ \ wedge = \ rho_ \ wedge \ ast c ^ 2 = \ frac {\ wedge c ^ 2} {8 \ pi G} $$
ダークエネルギー密度パラメーター、
$$ \ Omega_ \ wedge = \ frac {\ rho_ \ wedge} {\ rho_c} $$
$ \ Omega_ \ wedge $は、臨界密度に関するダークエネルギーの密度です。
$$ \ rho = \ rho_b + \ rho_ {DM} + \ rho_ \ wedge $$
宇宙をはじき、宇宙を拡大させるダークエネルギーについては多くの理論があります。1つの仮説は、この暗黒エネルギーが真空エネルギー密度である可能性があるというものです。空間自体が何らかのエネルギーを処理していて、空間の単位体積内のバリオニック物質、暗黒物質、および放射の量を数えるとき、空間に関連するエネルギーの量も数えていると仮定しますが、明確ではありませんダークエネルギーは実際には真空エネルギー密度です。
暗黒物質と放射線の密度とスケールファクターの関係は、
$$ \ rho_m \ propto \ frac {1} {a ^ 3} $$
$$ \ rho_m \ propto \ frac {1} {a ^ 4} $$
密度v / sスケールファクタープロットがあります。同じプロットで、$ \ rho_ \ wedge $は、スケールファクターに依存しない宇宙の膨張を伴う定数であることがわかります。
次の画像は、密度とスケール係数の関係を示しています。

‘ρ’ v/s ‘a’(時間に関連するスケールファクター)同じグラフでは、ダークエネルギーは定数としてモデル化されています。したがって、現在の宇宙で測定する暗黒エネルギーが何であれ、それは一定です。
覚えておくべきポイント
宇宙マイクロ波背景放射を使用した独立した観測は、k = 0であることを示しています。
$ \ rho_ \ wedge $は、スケールファクターに依存しない宇宙の膨張を伴う定数です。
重力も時間とともに変化しています。 modified Newtonian dynamics。
この章では、スパイラル銀河の回転曲線と暗黒物質の証拠について説明します。
暗黒物質と暗黒物質に関する観察事実
暗黒物質の初期の証拠は study of the Kinematics of Spiral Galaxy。
太陽は私たちの銀河の中心から30,000光年オフセットされています。銀河中心速度は220km / sです。
速度220km / sが100km / sまたは500km / sではないのはなぜですか?オブジェクトの円運動を支配するものは何ですか?
半径内に囲まれた質量は、宇宙の速度を検出するのに役立ちます。
天の川または渦巻銀河の回転–差動回転
Angular Velocity 中心からの距離によって異なります。
軌道の期間は、中心からの距離によって異なります。
銀河中心に近い材料は期間が短く、銀河中心から遠い材料は期間が長くなります。
回転曲線
で速度変化を予測します Galactic centric radius。速度を与える曲線は、軌道半径によって変化します。
物が動くのを見ると、回転に影響を与えるのは重力だと思います。
質量分布は半径によって異なります。物質密度は回転曲線を予測します。半径によって変化する物質密度に基づく回転曲線。
表面の明るさ
パッチを選択して、どれだけの光が出ているかを確認します。
パッチから来る光の量は、表面輝度と呼ばれます。
その単位は mag/arcsec2。
表面の明るさが半径によって変化することがわかった場合、発光物質は半径によって変化することがわかります。
$$ \ mu(r)\ propto exp \ left(\ frac {-r} {h_R} \ right)$$
$ h_R $はスケールの長さです。$ \ mu(r)= \ mu_o \ ast exp \ left(\ frac {-r} {h_R} \ right)$
$ h_R $は、天の川のほぼ3kpcです。
渦巻銀河
天文学者が回転曲線を理解するために、彼らは銀河を2つの成分に分割します。
- Disk
- Bulge
次の画像は、中央の球形の膨らみ+円形の円盤を示しています。恒星とガスの分布は、バルジとディスクで異なります。

渦巻銀河の運動学
-
任意のオブジェクトの円速度–バルジの場合は(r <Rb)です。
$$ V ^ 2(r)= G \ ast \ frac {M(r)} {r} $$
$$ M(r)= \ frac {4 \ pi r ^ 3} {3} \ ast \ rho_b $$
-
ディスクの場合–(Rb <r <Rd)
$$ V ^ 2(r)= G \ ast \ frac {M(r)} {r} $$
バルジの星の密度はほぼ一定です。
バルジ内の密度は一定です(バルジ内の距離によって変化しません)。
ディスクでは、恒星の密度は半径とともに減少します。半径が大きくなり、発光物質が減少します。
一括– $ V(r)\ propto r $
ディスク内– $ V(r)\ propto 1 / \ sqrt {r} $
渦巻銀河の回転曲線
を通って Spectroscopy (近くの銀河–空間的に分解された銀河)、回転曲線を作成します。
上で述べたように、回転曲線は外側の領域で平坦であることがわかります。つまり、外側の領域では物事が速く動いています。これは通常、この形式ではないと予想されます。
軌道速度は、内側の領域の半径が大きくなるにつれて増加しますが、外側の領域では平坦になります。
ダークマター
暗黒物質は宇宙の非発光成分であると言われています。以下の指針を通して暗黒物質について理解しましょう。
平らな回転曲線は、渦巻銀河における星とガスの分布について私たちが見ているものとは逆です。
ディスクの表面光度は半径とともに指数関数的に低下します。これは、発光物質、主に星の質量が銀河中心の周りに集中していることを意味します。
回転曲線の平坦化は、ある半径内の銀河の総質量が r の増加とともに常に増加しています r。
これは、電磁放射を放出していないこれらの銀河に大量の目に見えない重力質量がある場合にのみ説明できます。
渦巻銀河の回転曲線の測定は、暗黒物質の最も説得力のある一連の証拠の1つです。
暗黒物質の証拠
欠落質量–発光質量の10倍。
この暗黒物質のほとんどは銀河のハローにあるに違いありません。ディスク内の大量の暗黒物質は、潮汐力に対するディスクの長期的な安定性を妨げる可能性があります。
ディスク内の暗黒物質のごく一部はバリオンである可能性があります–薄暗い星(褐色矮星、黒色矮星)、およびコンパクト星の残骸(中性子星、ブラックホール)。しかし、そのようなバリオン暗黒物質は、銀河の失われた質量のフルスケールを説明することはできません。
暗黒物質の密度プロファイル– $ M(r)\ propto r $および$ \ rho(r)\ propto r ^ {− 2} $。
渦巻銀河の回転曲線データは、それらのハローに分布する暗黒物質と一致しています。
このダークハローは、銀河の総質量の大部分を占めています。
すべてのバリオン物質(星、星団、ISMなど)は、この暗黒物質ハローの重力ポテンシャルによってまとめられています。
結論
暗黒物質は、通常の物質との重力相互作用によってのみ検出されています。光との相互作用(電磁力なし)はまだ観察されていません。
Neutrinos−電荷が少なく、相互作用が弱いが、質量が少なすぎる(<0.23eV)。DM粒子は、構造形成を説明するためにE> 10eV程度である必要があります。
弱く相互作用する巨大粒子(WIMPS)は、暗黒物質の原因となる可能性があります。
覚えておくべきポイント
銀河中心に近い物質は、より短い期間を持ちます。
バルジの星の密度はほぼ一定です。
ディスクの表面光度は、半径とともに指数関数的に低下します。
ディスク内の大量の暗黒物質は、潮汐力に対するディスクの長期安定性を妨げる可能性があります。
暗黒物質の最初の直接的な証拠は Frids Ricky。彼は初めて暗黒物質を明らかにしたいくつかの観察をしました。彼の観測は、銀河団内の全体的な動きを考慮しました。
拡張オブジェクトは銀河団であり、バインドされた構造と見なされます。これらの銀河はクラスターの中心に対して動いていますが、飛んではいきません。銀河の全体的な動きを見てみましょう。
仮定:速度は潜在的な可能性を表しています
すべての銀河は、クラスター内で独自の固有運動を持ち、 Hubble Flow Component。小さい銀河は小さく、ほとんどの光はM31とMWから来ており、いくつかの矮小銀河があります。大まかな分析では、M31とMWのみを使用して、ローカルグループの動的質量を評価できます。
私たちとM31の間には相対速度があります。粗雑ですが、本当です。物語は、M31とMWが互いに離れていったクラスターのメンバーであったため、互いに接近していたときに始まります。しばらくすると、それらは最大の分離に達し、次に互いに近づきます。
到達できる最大の分離は$ r_ {max} $であるとしましょう。今、彼らは呼ばれる分離を持っていますr。しましょうMMWとM31の合計質量になります。$ r_ {max} $にいつ到達したかはわかりません。
$$ \ frac {GM} {r_ {max}} = \:Potential \:at \:r_ {max} $$
これらの銀河がある瞬間rで互いに接近していたとき、システムのエネルギーは次のようになります。
$$ \ frac {1} {2} \ sigma ^ 2 = \ frac {GM} {r} = \ frac {GM} {r_ {max}} $$
σは両方の銀河の相対速度です。 M は換算質量のみですが、テスト質量は1です。σは距離における任意のオブジェクトの速度です。 rクラスターの中心から。ビリアル定理が成り立つため、このクラスターは動的方程式にあると考えられます。したがって、銀河は異なる速度で来ることはできません。
これらの銀河が最大距離に到達するのにどれくらいの時間がかかりますか?
これを理解するために、次の方程式を考えてみましょう。
$$ \ frac {1} {2} \ left(\ frac {dr} {dt} \ right)^ 2 = \ frac {GM} {r}-\ frac {GM} {r_ {max}} $$
$$ t_ {max} = \ int_ {0} ^ {r_ {max}} dt = \ int_ {0} ^ {r_ {max}} \ frac {dr} {\ sqrt {2GM}} \ left(\ frac {1} {r}-\ frac {1} {r_ {max}} \ right)^ 2 $$
$$ t_ {max} = \ frac {\ pi r_ {max} ^ {\ frac {3} {2}}} {2 \ sqrt {2GM}} $$
ここで、M =ローカルグループの動的質量。衝突の開始から終了までの合計時間は$ 2t_ {max} $です。したがって、
$$ 2t_ {max} = t_0 + \ frac {D} {\ sigma} $$
そして$ t_0 $は宇宙の現代です。
実際の$ t_ {max} <RHS $の場合、時間の下限があります。$ D / \ sigma $は、それらが再び衝突する時間です。ここでは、σが一定であると仮定しています。
$$ t_ {max} = \ frac {t_0} {2} + \ frac {D} {2 \ sigma} $$
$$ r_ {max} = t_ {max} \ times \ sigma = 770K_ {pc} $$
ここで、σ= MWとM31の間の相対速度。
$$ M_ {dynamic} = 3 \ times 10 ^ {12} M_0 $$
$$ M_ {MW} ^ {lum} = 3 \ times 10 ^ {10} M_0 $$
$$ M_ {M31} ^ {lum} = 3 \ times 10 ^ {10} M_0 $$
しかし実際には、動的質量はクラスター内のすべての銀河を考慮して見出されます。不足している質量は暗黒物質であり、Frids Rickyかみのけ座銀河団の銀河の動きが速すぎることに気づきました。彼は、中性子星が発見された翌年に中性子星の存在を予測し、パロマー望遠鏡を使用して超新星を見つけました。
覚えておくべきポイント
暗黒物質の最初の直接的な証拠は Frids Ricky。
拡張オブジェクトは銀河団であり、それらは考慮されます bound structures。
Dynamic mass クラスター内のすべての銀河を考慮して発見されました。
この章では、密度とハッブルのパラメータについて説明します。
ハッブルパラメータ
ハッブルパラメータは次のように定義されます-
$$ H(t)\ equiv \ frac {da / dt} {a} $$
これは、スケールファクターがどれだけ急速に変化するかを測定します。より一般的には、スケールファクターの展開はフリードマン方程式によって決定されます。
$$ H ^ 2(t)\ equiv \ left(\ frac {\ dot {a}} {a} \ right)^ 2 = \ frac {8 \ pi G} {3} \ rho- \ frac {kc ^ 2} {a ^ 2} + \ frac {\ wedge} {3} $$
どこ、 ∧ は宇宙定数です。
平らな宇宙の場合、k = 0であるため、フリードマン方程式は次のようになります。
$$ \ left(\ frac {\ dot {a}} {a} \ right)^ 2 = \ frac {8 \ pi G} {3} \ rho + \ frac {\ wedge} {3} $$
物質が支配する宇宙の場合、密度は次のように変化します。
$$ \ frac {\ rho_m} {\ rho_ {m、0}} = \ left(\ frac {a_0} {a} \ right)^ 3 \ Rightarrow \ rho_m = \ rho_ {m、0} a ^ {- 3} $$
そして、放射線が支配的な宇宙の場合、密度は次のように変化します。
$$ \ frac {\ rho_ {rad}} {\ rho_ {rad、0}} = \ left(\ frac {a_0} {a} \ right)^ 4 \ Rightarrow \ rho_ {rad} = \ rho_ {rad、 0} a ^ {-4} $$
現在、私たちは物質が支配する宇宙に住んでいます。したがって、$ \rho≡\ rho_m $を考慮すると、次のようになります。
$$ \ left(\ frac {\ dot {a}} {a} \ right)^ 2 = \ frac {8 \ pi G} {3} \ rho_ {m、0} a ^ {-3} + \ frac {\ wedge} {3} $$
宇宙定数と暗黒エネルギー密度は次のように関係しています。
$$ \ rho_ \ wedge = \ frac {\ wedge} {8 \ pi G} \ Rightarrow \ wedge = 8 \ pi G \ rho_ \ wedge $$
これから、次のようになります。
$$ \ left(\ frac {\ dot {a}} {a} \ right)^ 2 = \ frac {8 \ pi G} {3} \ rho_ {m、0} a ^ {-3} + \ frac {8 \ pi G} {3} \ rho_ \ wedge $$
また、臨界密度とハッブル定数は次のように関係しています。
$$ \ rho_ {c、0} = \ frac {3H_0 ^ 2} {8 \ pi G} \ Rightarrow \ frac {8 \ pi G} {3} = \ frac {H_0 ^ 2} {\ rho_ {c、 0}} $$
これから、次のようになります。
$$ \ left(\ frac {\ dot {a}} {a} \ right)^ 2 = \ frac {H_0 ^ 2} {\ rho_ {c、0}} \ rho_ {m、0} a ^ {- 3} + \ frac {H_0 ^ 2} {\ rho_ {c、0}} \ rho_ \ wedge $$
$$ \ left(\ frac {\ dot {a}} {a} \ right)^ 2 = H_0 ^ 2 \ Omega_ {m、0} a ^ {-3} + H_0 ^ 2 \ Omega _ {\ wedge、0 } $$
$$(\ dot {a})^ 2 = H_0 ^ 2 \ Omega_ {m、0} a ^ {-1} + H_0 ^ 2 \ Omega _ {\ wedge、0} a ^ 2 $$
$$ \ left(\ frac {\ dot {a}} {H_0} \ right)^ 2 = \ Omega_ {m、0} \ frac {1} {a} + \ Omega _ {\ wedge、0} a ^ 2 $$
$$ \ left(\ frac {\ dot {a}} {H_0} \ right)^ 2 = \ Omega_ {m、0}(1 + z)+ \ Omega _ {\ wedge、0} \ frac {1} { (1 + z)^ 2} $$
$$ \ left(\ frac {\ dot {a}} {H_0} \ right)^ 2(1 + z)^ 2 = \ Omega_ {m、0}(1 + z)^ 3 + \ Omega _ {\ wedge 、0} $$
$$ \ left(\ frac {\ dot {a}} {H_0} \ right)^ 2 \ frac {1} {a ^ 2} = \ Omega_ {m、0}(1 + z)^ 3 + \ Omega_ {\ wedge、0} $$
$$ \ left(\ frac {H(z)} {H_0} \ right)^ 2 = \ Omega_ {m、0}(1 + z)^ 3 + \ Omega _ {\ wedge、0} $$
ここで、$ H(z)$は赤方偏移に依存するハッブルパラメーターです。これは、放射密度パラメーター$ \ Omega_ {rad} $と曲率密度パラメーター$ \ Omega_k $を含めるように変更できます。修正された方程式は次のとおりです。
$$ \ left(\ frac {H(z)} {H_0} \ right)^ 2 = \ Omega_ {m、0}(1 + z)^ 3 + \ Omega_ {rad、0}(1 + z)^ 4 + \ Omega_ {k、0}(1 + z)^ 2 + \ Omega _ {\ wedge、0} $$
$$または、\:\ left(\ frac {H(z)} {H_0} \ right)^ 2 = E(z)$$
$$または、\:H(z)= H_0E(z)^ {\ frac {1} {2}} $$
どこ、
$$ E(z)\ equiv \ Omega_ {m、0}(1 + z)^ 3 + \ Omega_ {rad、0}(1 + z)^ 4 + \ Omega_ {k、0}(1 + z) ^ 2 + \ Omega _ {\ wedge、0} $$
これは、ハッブルパラメータが時間とともに変化することを示しています。
のために Einstein-de Sitter ユニバース、$ \ Omega_m = 1、\ Omega_ \ wedge = 0、k = 0 $。
これらの値を入力すると、次のようになります。
$$ H(z)= H_0(1 + z)^ {\ frac {3} {2}} $$
これは、アインシュタイン-ドジッター宇宙のハッブルパラメーターの時間発展を示しています。
密度パラメータ
密度パラメーター$ \ Omega $は、実際の(または観測された)密度ρと臨界密度$ \ rho_c $の比率として定義されます。任意の量$ x $の対応する密度パラメーターについて、$ \ Omega_x $は数学的に次のように表すことができます。
$$ \ Omega_x = \ frac {\ rho_x} {\ rho_c} $$
検討中のさまざまな量について、次の密度パラメータを定義できます。
| S.No. | 量 | 密度パラメータ |
|---|---|---|
| 1 | バリオン | $ \ Omega_b = \ frac {\ rho_b} {\ rho_c} $ |
| 2 | マター(バリオン+ダーク) | $ \ Omega_m = \ frac {\ rho_m} {\ rho_c} $ |
| 3 | ダークエネルギー | $ \ Omega_ \ wedge = \ frac {\ rho_ \ wedge} {\ rho_c} $ |
| 4 | 放射線 | $ \ Omega_ {rad} = \ frac {\ rho_ {rad}} {\ rho_c} $ |
記号が通常の意味を持つ場所。
覚えておくべきポイント
スケールファクターの進化は、 Friedmann Equation。
H(z) 赤方偏移に依存するハッブルパラメータです。
ザ・ Hubble Parameter 時間とともに変化します。
ザ・ Density Parameter 臨界密度に対する実際の(または観測された)密度の比率として定義されます。
前の章で説明したように、ハッブルパラメータの時間発展は次の式で与えられます。
$$ H(z)= H_0E(z)^ {\ frac {1} {2}} $$
どこ z 赤方偏移であり、 E(Z) は−
$$ E(z)\ equiv \ Omega_ {m、0}(1 + z)^ 3 + \ Omega(1 + z)^ 4 + \ Omega_ {k、0}(1 + z)^ 2 + \ Omega ^ {\ wedge、0} $$
宇宙の膨張が一定である場合、宇宙の真の年齢は次のように与えられます-
$$ t_H = \ frac {1} {H_0} $$
それが物質が支配する宇宙、すなわちアインシュタインのドジッター宇宙である場合、宇宙の真の年齢は次の式で与えられます。
$$ t_H = \ frac {2} {3H_0} $$
スケールと赤方偏移は次のように定義されます-
$$ a = \ frac {a_0} {1 + z} $$
宇宙論的パラメータによる宇宙の年齢は次のように導き出されます。
ハッブルパラメータは次の式で与えられます。
$$ H = \ frac {\ frac {da} {dt}} {a} $$
差別化すると、次のようになります。
$$ da = \ frac {-dz} {(1 + z)^ 2} $$
どこ a0 = 1 (スケールファクターの現在価値)
$$ \ frac {\ mathrm {d} a} {\ mathrm {d} t} = \ frac {-1} {(1 + z)^ 2} $$
$$ \ frac {\ mathrm {d} a} {\ mathrm {d} t} = \ frac {\ mathrm {d} a} {\ mathrm {d} t} \ frac {\ mathrm {d} z} { \ mathrm {d} t} $$
$$ H = \ frac {\ dot {a}} {a} = \ frac {\ mathrm {d} a} {\ mathrm {d} t} \ frac {\ mathrm {d} z} {\ mathrm {d } t} \ frac {1 + z} {1} $$
$$ \ frac {\ dot {a}} {a} = \ frac {-1} {1 + z} \ frac {\ mathrm {d} z} {\ mathrm {d} t} \ frac {1} { 1} $$
$$ H(z)= H_0E(z)^ {\ frac {1} {2}} $$
$$ dt = \ frac {-dz} {H_0E(z)^ {\ frac {1} {2}}(1 + z)} $$
任意の赤方偏移で宇宙の年齢を見つけたい場合 ‘z’ 次に−
$$ t(z)= \ frac {1} {H_0} \ int _ {\ infty} ^ {z_1} \ frac {-1} {E(z)^ {\ frac {1} {2}}(1+ z)} dz $$
どこ k は曲率密度パラメータであり、−
$$ E(z)\ equiv \ Omega_ {m、0}(1 + z)^ 3 + \ Omega_ {rad、0}(1 + z)^ 4 + \ Omega_ {k、0}(1 + z) ^ 2 + \ Omega _ {\ wedge、0} $$
宇宙の現在の年齢を計算するには、 z1 = 0。
$$ t(z = 0)= t_ {age} = t_0 = \ frac {1} {H_0} \ int _ {\ infty} ^ {z_1} \ frac {-1} {E(z)^ {\ frac { 1} {2}}(1 + z)} dz $$
アインシュタインデシッターモデル、つまり$ \ Omega_m = 1 $、$ \ Omega_ {rad} = 0 $、$ \ Omega_k = 0 $、$ \ Omega_ \ wedge = 0 $の場合、宇宙の年齢の方程式は次のようになります。 −
$$ t_ {age} = \ frac {1} {H_0} \ int_ {0} ^ {\ infty} \ frac {1} {(1 + z)^ {\ frac {5} {2}}} dz $ $
積分を解いた後、次のようになります。
$$ t_H = \ frac {2} {3H_0} $$
夜空は Cosmic Time Machine.遠くの惑星、星、銀河を観察するときはいつでも、何時間、何世紀、あるいは何千年も前のようにそれを見ています。これは、光が有限の速度(光速)で移動し、宇宙内の距離が長いため、現在のオブジェクトではなく、光が放出されたときのオブジェクトが表示されるためです。ここで地球上で光を検出してから、元々光源から放出されたときまでの経過時間は、Lookback Time (tL(z1))。
したがって、ルックバック時間は次の式で与えられます。
$$ t_1(z_1)= t_0-t(z_1)$$
アインシュタインのドジッター宇宙のルックバック時間は-
$$ t_L(z)= \ frac {2} {3H_0} \ left [1- \ frac {1} {(1 + z)^ {\ frac {3} {2}}} \ right] $$
覚えておくべきポイント
遠くの惑星、星、銀河を観察するときはいつでも、何時間、何世紀、あるいは何千年も前のようにそれを見ています。
ここ地球上で光を検出してから、最初に光源から放射されてからの経過時間は、ルックバック時間と呼ばれます。
この章では、角直径距離とは何か、そしてそれが宇宙論でどのように役立つかを理解します。
現在の宇宙のために-
$ \ Omega_ {m、0} \:= \:0.3 $
$ \ Omega _ {\ wedge、0} \:= \:0.69 $
$ \ Omega_ {rad、0} \:= \:0.01 $
$ \ Omega_ {k、0} \:= \:0 $
これまで2種類の距離を研究してきました-
Proper distance (lp) −光子がソースから私たちまで移動する距離。 Instantaneous distance。
Comoving distance (lc) −拡張しない空間内のオブジェクト間の距離。 distance in a comoving frame of reference。
赤方偏移の関数としての距離
ある時に光子を放射する銀河を考えてみましょう t1 これは、オブザーバーによって検出されます。 t0。銀河までの適切な距離は次のように書くことができます-
$$ l_p = \ int_ {t_1} ^ {t_0} cdt $$
銀河の赤方偏移を z、
$$ \ Rightarrow \ frac {\ mathrm {d} z} {\ mathrm {d} t} =-\ frac {1} {a ^ 2} \ frac {\ mathrm {d} a} {\ mathrm {d} t} $$
$$ \ Rightarrow \ frac {\ mathrm {d} z} {\ mathrm {d} t} =-\ frac {\ frac {\ mathrm {d} a} {\ mathrm {d} t}} {a} \ frac {1} {a} $$
$$ \したがって、\ frac {\ mathrm {d} z} {\ mathrm {d} t} =-\ frac {H(z)} {a} $$
さて、いつでも銀河の共動距離 t −になります
$$ l_c = \ frac {l_p} {a(t)} $$
$$ l_c = \ int_ {t_1} ^ {t_0} \ frac {cdt} {a(t)} $$
zに関しては、
$$ l_c = \ int_ {t_0} ^ {t_1} \ frac {cdz} {H(z)} $$
距離を見つける方法は2つあり、次のとおりです。
フラックスと光度の関係
$$ F = \ frac {L} {4 \ pi d ^ 2} $$
どこ d ソースでの距離です。
ソースの角直径距離
ソースのサイズがわかっている場合、その角度幅から、観測者からの距離がわかります。
$$ \ theta = \ frac {D} {l} $$
どこ l ソースの角直径距離です。
θ ソースの角度サイズです。
D ソースのサイズです。
サイズDと角サイズの銀河を考えてみましょう dθ。
私達はことを知っています、
$$ d \ theta = \ frac {D} {d_A} $$
$$ \したがって、D ^ 2 = a(t)^ 2(r ^ 2 d \ theta ^ 2)\ quad \なぜなら、dr ^ 2 = 0; \:d \ phi ^ 2 \約0 $$
$$ \ Rightarrow D = a(t)rd \ theta $$
変化 r に rc、銀河の共動距離、私たちは-を持っています
$$ d \ theta = \ frac {D} {r_ca(t)} $$
ここで、 t = t0、銀河までの現在の距離を測定することになります。だがD光子の放出時に測定されます。したがって、を使用してt = t0、銀河までの距離が長くなるため、銀河のサイズが過小評価されます。したがって、時間を使用する必要がありますt1。
$$ \したがって、d \ theta = \ frac {D} {r_ca(t_1)} $$
これを前の結果と比較すると、次のようになります。
$$ d_ \ wedge = a(t_1)r_c $$
$$ r_c = l_c = \ frac {d_ \ wedge} {a(t_1)} = d_ \ wedge(1 + z_1)\ quad \ due to 1 + z_1 = \ frac {1} {a(t_1)} $$
したがって、
$$ d_ \ wedge = \ frac {c} {1 + z_1} \ int_ {0} ^ {z_1} \ frac {dz} {H(z)} $$
dA オブジェクトの角直径距離です。
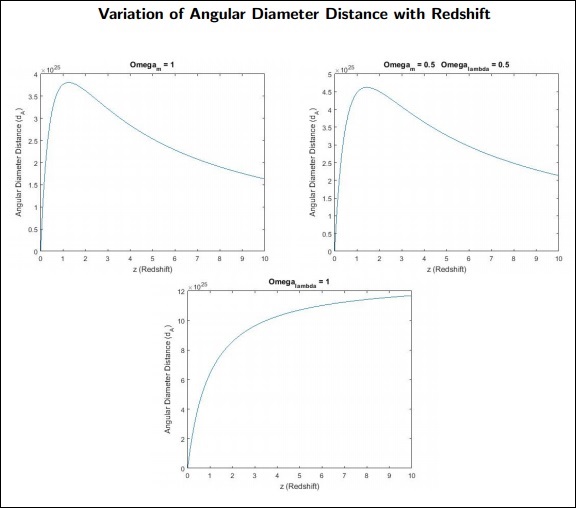
覚えておくべきポイント
ソースのサイズがわかっている場合、その角度幅から、観測者からの距離がわかります。
適切な距離とは、光子が光源から私たちまで移動する距離です。
共動距離は、拡張しない空間内のオブジェクト間の距離です。
前の章で説明したように、赤方偏移での光源までの角直径距離 z −で与えられます
$$ d_ \ wedge(z_ {gal})= \ frac {c} {1 + z_ {gal}} \ int_ {0} ^ {z_ {gal}} \ frac {1} {H(z)} dz $ $
$$ d_ \ wedge(z_ {gal})= \ frac {r_c} {1 + z_ {gal}} $$
ここで、$ r_c $は共動距離です。
光度距離は宇宙論に依存し、観測されたフラックスが到達する距離として定義されます f オブジェクトからです。
遠方の物体の固有の光度$ d_L $がわかっている場合、-によって決定されるフラックス$ f $を測定することにより、その光度を計算できます。
$$ d_L(z)= \ sqrt {\ frac {L} {4 \ pi f}} $$
光子エネルギーは赤方偏移します。
$$ \ frac {\ lambda_ {obs}} {\ lambda_ {emi}} = \ frac {a_0} {a_e} $$
ここで、$ \ lambda_ {obs}、\ lambda_ {emi} $が観測され、放出される波長と$ a_0、a_e $は対応するスケールファクターです。
$$ \ frac {\ Delta t_ {obs}} {\ Delta t_ {emi}} = \ frac {a_0} {a_e} $$
ここで、$ \ Delta_t {obs} $は光子の時間間隔として観測され、$ \ Delta_t {emi} $はそれらが放出される時間間隔です。
$$ L_ {emi} = \ frac {nhv_ {emi}} {\ Delta t_ {emi}} $$
$$ L_ {obs} = \ frac {nhv_ {obs}} {\ Delta t_ {obs}} $$
$ \ Delta t_ {obs} $は、検出器がすべての光子を受信する必要があるため、$ \ Delta t_ {emi} $よりも時間がかかります。
$$ L_ {obs} = L_ {emi} \ left(\ frac {a_0} {a_e} \ right)^ 2 $$
$$ L_ {obs} <L_ {emi} $$
$$ f_ {obs} = \ frac {L_ {obs}} {4 \ pi d_L ^ 2} $$
非膨張宇宙の場合、光度距離は共動距離と同じです。
$$ d_L = r_c $$
$$ \ Rightarrow f_ {obs} = \ frac {L_ {obs}} {4 \ pi r_c ^ 2} $$
$$ f_ {obs} = \ frac {L_ {emi}} {4 \ pi r_c ^ 2} \ left(\ frac {a_e} {a_0} \ right)^ 2 $$
$$ \ Rightarrow d_L = r_c \ left(\ frac {a_0} {a_e} \ right)$$
放出オブジェクト$ L_ {emi} $ −の光度を計算するための光度距離$ d_L $を見つけています。
Interpretation −赤方偏移がわかっている場合 zどんな銀河でも、$ d_A $を見つけることができ、そこから$ r_c $を計算することができます。これは、$ d_L $を見つけるために使用されます。
$ d_Lの場合!= r_c(a_0 / a_e)$の場合、$ f_ {obs} $からLemiを見つけることができません。
光度距離$ d_L $と角径距離$ d_A。$の関係
私たちはそれを知っています-
$$ d_A(z_ {gal})= \ frac {d_L} {1 + z_ {gal}} \ left(\ frac {a_0} {a_e} \ right)$$
$$ d_L =(1 + z_ {gal})d_A(z_ {gal})\ left(\ frac {a_0} {a_e} \ right)$$
光子が放出されるときのスケール係数は、次の式で与えられます。
$$ a_e = \ frac {1} {(1 + z_ {gal})} $$
現在の宇宙のスケールファクターは-
$$ a_0 = 1 $$
$$ d_L =(1 + z_ {gal})^ 2d_ \ wedge(z_ {gal})$$
$ d_L $または$ d_A $のどちらを選択しますか?
既知のサイズの銀河とその大きさを計算するための赤方偏移の場合、$ d_A $が使用されます。
見かけの等級が与えられた銀河がある場合、その大きさを調べるために、$ d_L $が使用されます。
Example −等しい赤方偏移(z = 1)の2つの銀河が与えられ、空の平面内でそれらが次のように分離されている場合 2.3 arc sec では、これら2つの間の最大の物理的分離はどれくらいですか?
これには、次のように$ d_A $を使用します-
$$ d_A(z_ {gal})= \ frac {c} {1 + z_ {gal}} \ int_ {0} ^ {z_ {gal}} \ frac {1} {H(z)} dz $$
ここで、z = 1は、銀河の宇宙論的パラメーターに基づいてH(z)を置き換えます。
覚えておくべきポイント
光度距離は cosmology。
遠方の物体の固有の光度$ d_L $がわかっている場合、フラックスを測定することでその光度を計算できます。 f。
非膨張宇宙の場合、光度距離は comoving distance。
光度距離は常によりも大きい Angular Diameter Distance。
任意の赤方偏移(z)に対して、距離に2つの値があります-
- 角直径距離(d A)
- 光度距離(d L)
宇宙には「宇宙論的」距離の独自の定義はありません。距離の選択は、アプリケーションの目的と利便性によって異なります。
オブジェクトの角度サイズがredshiftによってどのように変化するかについて予測される傾向をテストするには、空に標準サイズの物差しが必要です。これは、次のようなオブジェクトである必要があります。
は非常に明るいため、z> 1で検出できます。
は非常に大きいので、その角度サイズを解決できます。
宇宙論的に有意な時間にわたって形態学的に進化していません(z〜1は約7 Gyrの振り返り時間に対応します)。
一部の天体(cD銀河など)は最初の2つの基準を満たしています。しかし、ほとんどすべてのオブジェクトは、時間とともに形態学的に進化することがわかっています。一般に、天体物理学的オブジェクト(拡張ソース)は、まだ形成されているため、過去には本質的に小さくなる傾向があります。
光度距離
光度距離は宇宙論に依存します。光度距離の宇宙論への依存性は、それを宇宙論的パラメーターの有用な尺度にします。
本質的に進化せず、局所から高赤方偏移宇宙に存在する標準光源を見つけることができれば、宇宙論的パラメーターを推定することができます。
標準光源は、光源ごとに光度に違いがない光源です。標準的なろうそくの推定光度の違いは、宇宙論によるものでなければならないという前提があります。そのようなキャンドルの1つがIa型超新星です。
タイプ1a超新星(SNe)
これらは、連星である赤色巨星または同様の主系列星からの十分な質量降着後の白色矮星の爆発の結果です。赤色巨星が白色矮星のロッシュローブの距離よりも近づくと、物質移動が始まり、最終的に白色矮星が爆発して大量のエネルギーを放出し、コアを残しません。これらはタイプ1a超新星と呼ばれます。銀河におけるIa型超新星爆発の典型的な速度は1世紀に1回です。
タイプ1aSNeの検索は、さまざまなチームで行われています-
- ハイゼット超新星探索チーム(ブライアンシュミット、アダムリース他)
- 超新星宇宙論計画(ソール・パールマッター他)
と呼ばれる別の研究チームがありました Carnegie Supernovae Project 同様の結果を出した人。
異なるチームからの結果の類似性は、タイプ1aSNeの宇宙論的性質を示しています。したがって、それらは効率的な標準キャンドルです。
覚えておくべきポイント
宇宙には「宇宙論的」距離の独自の定義はありません。
角径距離と光度距離が最もよく使われます。
標準光源は、光源ごとに光度に違いがない光源です。
タイプ1aSNeは、標準光源であるという基準を満たしています。
CMB(宇宙マイクロ波背景放射)は、本質的に、物質と放射線が平衡状態にあったときの光子で構成されています。1920年代までに、膨張宇宙のアイデアが受け入れられ、いくつかの質問に答えることができました。しかし、より重い元素の豊富さと豊富さについての質問は答えられませんでした。さらに、膨張宇宙は、物質の密度が0まで減少するはずであることを意味しました。
1948年、ジョージ・ガンモウとラルフ・アルファーは、「ビッグバン」を使用して、より重い元素の起源と豊富さを説明しました。彼らはロバート・ハーマンとともに、「遺棄された放射線」または「ビッグバン」から残っている放射線の存在を予測しました。この残留放射の予測温度は50〜6 Kでした。1965年、ロバートディッケ、ジムピーブルズ、デビッドウィルキンソンが、アモペリジアスの研究グループとともにCMBを実験的に検出しました。
初期の宇宙は非常に熱く、エネルギーが高すぎて問題を中立に保つことができませんでした。したがって、物質はイオン化された形でした-Plasma。放射線(光子)と物質(プラズマ)は、主に次の3つのプロセスを通じて相互作用しました。
Compton Scattering −(主要な相互作用プロセス)高エネルギー光子と低エネルギー荷電粒子間の非弾性散乱。
Thomson Scattering −自由荷電粒子による光子の弾性散乱。
Inverse Compton Scattering−高エネルギー荷電粒子と低エネルギー光子。これらの相互作用により、最終的に物質と放射が熱平衡状態になりました。
熱平衡
熱平衡では、輻射は Planck Distribution of Energy、
$$ B_v(T)= \ frac {2hv ^ 3} {c(e ^ {hv / k_BT} -1)} $$
この間、相互作用が非常に頻繁であるため、光子の平均自由行程は非常に小さかった。宇宙は放射線に対して不透明でした。初期の宇宙は放射線が支配的でした。宇宙は、物質と放射が熱平衡に達し、それらのエネルギー密度が等しくなるように進化しました。これは、スケールファクターによる密度の変化を示すグラフから見ることができます。物質と放射線が平衡に達したスケールファクター(時間)(a(t))を見つけましょう。
$$ \ rho_m \ propto \ frac {1} {a ^ 3}、\:\ rho_r \ propto \ frac {1} {a ^ 4} $$
$$ \ frac {\ rho_ {m、t}} {\ rho_ {r、t}} = \ frac {\ Omega_ {m、t}} {\ Omega_ {r、t}} = \ frac {\ Omega_ { m、0}} {\ Omega_ {r、0}} a(t)$$
平衡状態では、
$$ \ frac {\ rho_ {m、t}} {\ rho_ {r、t}} = \ frac {\ Omega_ {m、t}} {\ Omega_ {r、t}} = 1 $$
$$ \ Rightarrow \ frac {\ Omega_ {m、0}} {\ Omega_ {r、0}} a(t)= 1 \:\ Rightarrow a(t)= 2.96 \ times 10 ^ {-4} $$
$ \ Omega_ {m、0} = 0.27 $および$ \ Omega_ {r、0} = 8 \ times 10 ^ {-5} $を使用します。このスケールファクターに対応する赤方偏移は、次の式で与えられます。
$$ z = 1 / a(t)-1 \約3375 $$
宇宙の膨張により、放射線のエネルギー密度が低下しました。したがって、宇宙は冷え始めました。光子のエネルギーが減少し始めると、中性原子が形成され始めました。したがって、1300年の赤方偏移のあたりで、中性水素が形成され始めました。この時代の気温は3000K近くでした。
物質と放射線の間の相互作用は非常にまれになり、したがって宇宙は放射線に対して透明になり始めました。この期間はと呼ばれます“Surface of last scattering”光子の平均自由行程が非常に大きくなったため、この期間以降、散乱はほとんど発生しませんでした。とも呼ばれます“Cosmic Photosphere”。
覚えておくべきポイント
CMBは、物質と放射線が平衡状態にあったときの光子で構成されています。
初期の宇宙は非常に熱く、エネルギーが高すぎて物質が中性を保つことができなかったため、イオン化された物質-プラズマとして存在していました。
コンプトン散乱、トムソン散乱、逆コンプトン散乱は、当時の3つの物質-放射線相互作用プロセスでした。
宇宙は、物質と放射が熱平衡に達するように進化しました。
まず、何が特徴的なのかを理解する必要があります decoupling。私たちは、物質が次の形でのみ存在するほどにエネルギーがはるかに高かったことを知っていますIonized Particles。したがって、デカップリングと再結合のエポックでは、水素のイオン化を可能にするためにエネルギーを低下させる必要がありました。デカップリング時の温度推定はおおよその計算が可能です。
これは次のように実行されました-
まず、基底状態の水素のイオン化のみを考慮してください。
$$ hv \ approx k_BT $$
$$ \したがってT \ approx \ frac {hv} {k_B} $$
基底状態の水素のイオン化には、 hν は13.6eVであり、 kB それは Boltzmann Constant8.61× 10-5 eV / Kで、温度が1.5×105ケルビンであることを示しています。
これは本質的に、温度が1.5×10 5 K未満の場合、中性原子が形成され始める可能性があることを示しています。
私たちは、バリオンの光子の割合が5×10程度であることを知っている10。したがって、光子の数が減少するグラフの末尾でも、水素原子をイオン化するのに十分な光子が存在します。さらに、電子と陽子の再結合は、基底状態の水素原子を保証するものではありません。励起状態は、イオン化に必要なエネルギーが少なくて済みます。したがって、正確な値を取得するには、規律ある統計分析をケースバイケースで実行する必要があります。計算により、温度は約3000Kに設定されます。
説明のために、水素を最初の励起状態に励起する場合を考えます。エネルギーが以上の光子数の比率の一般式ΔE, Nγ (> ΔE) フォトンの総数に Nγ −で与えられます
$$ \ frac {N_ \ gamma(> \ Delta E)} {N_ \ gamma} \ propto e ^ {\ frac {-\ Delta E} {kT}} $$
水素を最初の励起状態に励起する場合、 ΔE10.2eVです。ここで、バリオンごとに10.2を超えるエネルギーを持つ少なくとも1つの光子の非常に控えめな数を考慮すると(比率が5×10 10であることを念頭に置いて、式3から4800 Kとして温度を取得します(挿入されたNγ(> ΔE)= Np)。
これは、最初の励起状態で中性水素原子の集団を作成するための温度です。これをイオン化する温度は大幅に低くなります。したがって、我々は、1.5×10よりも良好な推定得る5寄り3000 K.の許容値であるKを
レッドシフト–温度の関係
赤方偏移と温度の関係を理解するために、以下の2つの方法を使用します。
方法1
から Wien’s Law、 私達はことを知っています
$$ \ lambda_mT =定数$$
これを赤方偏移に関連付けるために、-を使用します。
$$ 1 + z = \ frac {\ lambda_0} {\ lambda_e} $$
$λ_oT_o=λ_eT(z)$として、次のようになります。
$$ T(z)= T_0 \ frac {\ lambda_0} {\ lambda_e} = T_0(1 + z)$$
設定 To 現在の値3Kとして、特定の赤方偏移の温度値を取得できます。
方法2
頻度に関しては、次のことがわかります。
$$ v_0 = \ frac {v_e} {1 + z} $$
$$ B_vdv = \ frac {2hv ^ 3} {c ^ 2} \ frac {dv} {e ^ {hv / kT} -1} $$
これは、エネルギー間隔の光子の正味エネルギーについて教えてくれます。 hνは単一光子のエネルギーです。したがって、光子の数は次の式で求めることができます。Bνdν/hν。
$ n_ {νo} $が現在のもので、$ n_ {νe} $が放出されたものである場合、次のようになります。
$$ \ frac {n_ {v_e}} {n_ {v_0}} =(1 + z)^ 3 $$
単純化すると、次のようになります。
$$ n_ {v_0} = \ frac {2v_c ^ 2} {c ^ 2} \ frac {dv_c} {e ^ {hv / kT} -1} \ frac {1} {(1 + z)^ 3} = \ frac {2v_0 ^ 2} {c ^ 2} \ frac {dv_c} {e ^ {hv / kT} -1} $$
これは私たちに Wien’s Law 繰り返しますので、次のように結論付けることができます。
$$ T(z)= T_0 \ frac {\ lambda_0} {\ lambda_e} = T_0(1 + z)$$
覚えておくべきポイント
- 初期の宇宙は非常に暑く、約3000Kでした。
- 現在の測定では、宇宙の温度が3Kに近いことが明らかになっています。
- 時間をさかのぼると、それに比例して温度が上昇します。
この章では、CMB放射とCOBEの異方性、つまりCosmic BackgroundExplorerについて説明します。
CMBの一次異方性
宇宙からの観測と宇宙マイクロ波背景放射の一次異方性を理解するために、次の方程式を取り、以下に示すように理解しましょう。
CMB光子数密度(nγ、0)
$$ n _ {\ gamma、0} = \ frac {Total \:energy \:density} {Characteristic \:energy \:of \:Photons} $$
$$ n _ {\ gamma、0} = \ frac {aT_0 ^ 4} {k_BT_0} $$
$ k_B $は Boltzmann Constant $ T_0 $は present temperature of the universe。
現在の温度$(T_0)$を2.7 Kとして使用すると、現在のCMB光子数密度は400 cm -3として得られます。
宇宙の恒星の光子数密度は、大規模でははるかに小さい(〜= 10 -3 cm -3)。
バリオンと光子の比率(η)
CMBと混合される銀河からの恒星の寄与が無視できる場合、バリオンと陽子の比率は-です。
$$ \ eta = \ frac {n_ {b、0}} {n _ {\ gamma、0}} $$
現在価値は〜5× 10-10です。光子とバリオン数密度の両方がに比例するのでa−3、その後 η 時間とともに進化しません。
エネルギー密度
現在、数密度とは対照的に、物質のエネルギー密度は光子のエネルギー密度よりも支配的です。
バリオン物質のエネルギー密度= $ \ rho_ {b、0} c ^ 2 = 0.04 \ rho_cc ^ 2 = 2×10 ^ {− 9} ergcm ^ {−3} $。一方、放射線のエネルギー密度= $ aT_0 ^ 4 = 4 \ times 10 ^ {-13} ergcm {-3} $。
CMB放射の等方性
Penzias そして WilsonCMBが観測の範囲内で等方性であることがわかりました。限界は、機器の低い角度分解能と感度です。彼らは地球から観測を行ったため、大気中の水蒸気が1mmから1mまでの多くの波長を吸収するため、すべてのスペクトルで観測を行うことはできません。したがって、CMBをスペクトルとしてアサートすることはできません。
CMBは回転不変(等方性)であると考えられています。物質と放射線が平衡状態にあった時期があったので、宇宙の構造の形成は説明できません。物質の分布は等方性ではなく、間に巨大なボイドがある宇宙の網のように凝集しているため、CMBは銀河系外起源であると考えられています。
しかし、宇宙からの観測が始まると、CMBに異方性が見られ、物質中のこれらの異方性が構造の形成につながるという推論につながりました。
宇宙からのCMB放射の観測
CMBを観測するために打ち上げられた主な衛星は-
Cosmic Microwave Background Explorer (COBE、1989)
Wilkinson Microwave Anisotropy Probe (WMAP、2001)および
Planck (2009)。
COBE(Cosmic Background Explorer)
COBEには主に2つの楽器がありました。彼らはいたFar InfraRed Absolute Spectrometer (FIRAS)と Differential Microwave Radiometers(DMRアンテナ)。FIRASは、特定の方向に沿った波長の関数としてCMBの強度を測定します。一方、DMRには3つのアンテナがあり、3つの異なる方向からのCMBの強度の違いを測定します。次のポインタは、FIRASとDMRに関する詳細情報を提供します。
FIRASからのCMB観測は、CMB放射がT = 2.72528±0.00065Kでの黒体スペクトルに対応することを示しています。
DMRは、空のすべての方向で3つの周波数(31.5 GHz、53 GHz、90 GHz)を測定します。
DMR観測の「赤いバットマンのシンボル」は、前景放射(銀河拡散シンクロトロン放射)からのノイズです。
観測の強度変化は温度変化に対応します。ホットスポットとコールドスポットの存在は、CMB放射が異方性であることを証明しています。
CMBには歪みがないため、この異方性はデカップリング時に存在する必要があります。したがって、物質には他のポケットよりも密度の高いポケットがいくつかあるはずです。
COBEの結果
CMBスペクトル(エネルギーの関数としての強度)は、T = 2.7 Kに対応するほぼ完全な黒体です。CMB放射の比強度は、すべての方向でほぼ同じです。宇宙が大規模に等方性であることの確認(宇宙原理の仮定を検証します)。
データの分析は、COBE(DMR)の解像度でCMBスペクトルに温度異方性(「変動」)があることを示しました。
Resolution of COBE, WMAP, Planck
COBEに搭載されたDMR機器は、約7度の制限(最大)空間分解能を持っていました。
Wilkinson Microwave Anisotropy Probe(WMAP)の平均解像度は約0.7度でした。
プランク衛星の角度分解能は約10分角です。
覚えておくべきポイント
宇宙恒星の光子数密度は、CMBの光子数密度よりもはるかに小さいです。
物質のエネルギー密度は光子のエネルギー密度よりも高いので、私たちは物質が支配する宇宙に住んでいます。
COBE、WMAP、Planckは、CMBの異方性を測定および定量化するための取り組みです。
宇宙における構造の形成は、CMB異方性の結果です。
洗練され、修正された全天CMBマップを見ると、前景の汚染がたくさんあります。これは一種の anisotropyこれらのマップで。これらの前景の放出は天の川銀河からのものであることがわかります。CMBの強度は銀河面の平面に沿って高く、離れるにつれて強度が低下します。これらでは、銀河からのシンクロトロン放出である二次異方性を観測することができます。これらの排出物は前景の汚染を構成します。空からのCMB放射を見るには、これらの前景放射を差し引く必要があります。
次の画像は、前景放射を伴うCMBを示しています。

ダイポール異方性
CMB全天図で見つかった別の種類の異方性があります。これは双極子異方性と呼ばれます。それは初期の宇宙とは関係がありません。これは、球面調和関数を使用して表すことができます。球面上にパターンがあり、数学関数を使用してそれをマッピングしたい場合は、三角関数を使用してマッピングできます。したがって、マップするときは、すべての方向で同じである単極子、または180度回転したときにプロパティを反転する双極子にすることができます。同様に、四重極などがあります。複雑なパターンの場合、これらの単極子、双極子、四重極子などの合計として表すことができます。
CMBは、全天図の異方性の主な原因の1つがこの双極子異方性であるようにモデル化されていますが、CMBの原始的なモデリングではありません。これは下の画像で見ることができます。

私たちが見ることができる双極子の方向は、ランダムな方向ではありません。ダイポール異方性には方向性があります。特定の方向に沿ってCMB強度が見られます。この方向は、太陽系の速度ベクトルによるものです。地球の速度は、太陽または銀河の中心を基準にして表すことができます。地球が移動している方向では、青方偏移と赤方偏移が観測され、双極子はこの方向に沿っています。
上の画像は、銀河が特定の方向に動いているため、典型的な双極子の外観をしています。その結果、空の片側が赤方偏移で表示され、空の反対側が青方偏移で表示されます。この場合、赤方偏移は、光子の波長が長い=涼しいことを意味します(したがって、名前から逆に、上の図では青く見えます)。
地球は、ある瞬間に、太陽/銀河中心/空のCMBに対して特定の方向に動いていると言えます。次に、任意の角度を見てCMBの温度を測定すると、それは異なります。これは、青方偏移または赤方偏移のいずれかであり、空の光子の視線に依存する光子を測定しているためです。
覚えておくべきポイント
CMB全天図の前景汚染はCMBの異方性と呼ばれます。
これらの放出は、私たち自身の天の川銀河からのものです。
異方性には、ダイポール異方性と角度パワースペクトル異方性の2種類があります。
ダイポール異方性は特定の方向にありますが、角度パワースペクトル異方性はいたるところに広がっています。
地平線の長さは、「ビッグバン」から「再結合の時代」までの光子の移動距離です。1回目の角度スペクトラムのピークは、非常に特殊な長さスケールであり、θ=1◦(L = 180)です。
2点間の適切な距離は次の式で与えられます。
$$ r_p = \ int_ {0} ^ {t} cdt $$
我々は、T = TにT = 0の時間枠を取るときは、REC、その後、
$$ r_H = \ int_ {0} ^ {t_ {rec}} cdt $$
ここで、$ r_H $は適切な地平線距離です。
今、私たちはそれを知っています-
$$ \ dot {a} = \ frac {\ mathrm {d} a} {\ mathrm {d} t} $$
$$ dt = \ frac {da} {\ dot {a}} $$
t = 0の場合、a = 0です。
次に、$ t = t_ {rec}、a = a_0 /(1 + z_ {rec})$。
したがって、私たちは書くことができます、
$$ r_H(z_ {rec})= \ int_ {0} ^ {a_ {rec}} c \ frac {da} {aH} $$
$$ H(a_ {rec})= H(z_ {rec})= H_0 \ sqrt {\ Omega_ {m、0}} a ^ {-3/2} $$
間に Recombination period universe物質が支配的でした。すなわち、Ωrad << Ωmatter。したがって、放射線という用語は削除されます。
$$ r_H(z_ {rec})= \ frac {c} {H_0 \ sqrt {\ Omega_ {m、0}}} \ int_ {0} ^ {a_ {rec}} \ frac {da} {a ^ { -1/2}} $$
$$ r_H(z_ {rec})= \ frac {2c} {3H_0 \ sqrt {\ Omega_ {m、0}}} \ frac {1} {(1 + z_ {rec})^ {3/2}} $$
$$ \ theta_H(rec)= \ frac {r_H(z_ {rec})} {d_A(z_ {rec})} $$
既知のすべての値を方程式に入れると、これは0.5度に相当します。
ザ・ Electromagnetic radiation最後の散乱の表面から不透明です。互いに地平線内にある「ない」2つのポイントは、同じプロパティを持つ必要はありません。したがって、異なる温度値が得られます。
この表面上で互いに交差しなかった2つの点を取得できます。つまり、ある点では、宇宙は膨張のインフレーションモデルである光速よりも速く膨張しました。
覚えておくべきポイント
地平線の長さは、「ビッグバン」から「再結合の時代」までの光子の移動距離です。
再結合期間中、宇宙は物質が支配的でした。
電磁放射は、最後の散乱の表面から不透明です。
Astrobiology宇宙の生命の起源、進化、分布、そして未来の研究です。それは発見と検出に関係していますExtrasolar Planets。
Astrobiology 以下の点に対処します-
人生はどのように始まり、進化しますか?(生物学+地質学+化学+大気科学)
地球の向こうに生命に有利な世界はありますか?(天文学)
地球上の生命の未来はどうなるでしょうか?
Astronomy 以下の点に対処します-
他の星の周りの惑星系を検出する方法は?
方法の1つは直接イメージングですが、惑星は星に比べて非常に暗い光源であり、惑星からのわずかな光は親星からのまぶしさで失われる傾向があるため、これは非常に困難な作業です。
惑星がその親星に近く、高温である場合、コントラストはより良くなり、その結果、それは強い赤外線放射を放出します。赤外線領域で画像を作成できます。
太陽系外惑星の検出技術
太陽系外惑星を検出するための最も効率的な手法は次のとおりです。これらのそれぞれについても、後続の章で詳しく説明します。
視線速度法
ドップラー法とも呼ばれます。これで-
星の惑星系は、重心を中心に回転し、星がぐらつきます。
ぐらつきはによって検出することができます
定期的な赤/青のシフト。位置天文学-空の物体を非常に正確に測定します。
トランジット方式
トランジット法(ケプラー宇宙望遠鏡)を使用してサイズを調べます。連星系とは異なり、惑星ごとの星の明るさの低下は通常非常に少ないです。
ダイレクトイメージング
望遠鏡を使用して惑星をイメージングします。
視線速度法で行われたケーススタディを見てみましょう。
ケーススタディ
このケーススタディは、円軌道と空の平面に垂直な軌道の平面に関するものです。重心の周りの両方にかかる時間は同じになります。これは、2つのRedshiftまたはBlueshift間の時間差に等しくなります。
次の画像について考えてみます。

AとCで–全速力が測定されます。Cでは、速度はゼロです。
Vrmax = V *は、星の真の速度です。
Pは、星と惑星の期間です。
θは軌道の位相です。
星の質量-M *、軌道半径a *、惑星の質量mp。
重心方程式から、
$$ m_p a_p = M_ \ ast a_ \ ast $$
速度方程式から、
$$ V_ \ ast = \ frac {2 \ pi a_ \ ast} {P} $$
$$ \ Rightarrow a_ \ ast = \ frac {PV_ \ ast} {2 \ pi} $$
から Kepler’s Law、
$$ P ^ 2 = \ frac {4 \ pi ^ 2a_p ^ 3} {GM_ \ ast} $$
$$ \ Rightarrow a_p = \ left(\ frac {P ^ 2GM_ \ ast} {4 \ pi ^ 2} \ right)^ {1/3} $$
上記の式から、次のようになります。
$$ \ Rightarrow m_p = \ left(\ frac {P} {2 \ pi G} \ right)^ {1/3} M_ \ ast ^ {2/3} V_ \ ast $$
$ m_p、a_p $、$ a_ \ ast $を取得します。
上記の方程式は、星に近いほとんどの巨大な惑星に偏っています。
覚えておくべきポイント
宇宙生物学は、宇宙における生命の起源、進化、分布、そして未来の研究です。
太陽系外惑星を検出する手法は、視線速度法、トランジット法、ダイレクトイメージングなどです。
ぐらつきは、周期的な赤/青のシフトと位置天文学によって検出できます。
視線速度法は、星に近い巨大な惑星を検出することに偏っています。
前章では、円軌道について、軌道面と空面が垂直な場合の視線速度法について説明しました。ここでは、軌道面と空の面が円軌道に対して垂直でない場合のもう1つのケースを扱います。
軌道面が空の面に対してある角度(垂直ではない)の場合、次のような状況になります。

この場合、それらが垂直であるとき、真の速度を測定できる2つのポイントがありました。しかし、ここでは、それは不可能です。すべての点で、真の速度の成分のみを測定できます。v。
$$ v_r = v \:sin(i)cos(\ theta)$$
どこ θ時間に依存する量である軌道の位相です。傾斜角i一方、時間に依存しません。したがって、
$$(v_r)_ {max} = v \:sin(i)$$
観測された視線速度曲線は次の形式になります-

軌道面が空に垂直なとき−
$$ m_p = \ left(\ frac {P} {2 \ pi G} \ right)^ {\ frac {1} {3}}(M_ \ ast)^ {\ frac {2} {3}} v $ $
どこ mp, P, G, M∗はそれぞれ惑星の質量、公転周期、万有引力定数、星の質量です。ただし、この場合、次のように変更する必要があります-
$$ m_psin(i)= \ left(\ frac {P} {2 \ pi G} \ right)^ {\ frac {1} {3}}(M_ \ ast)^ {\ frac {2} {3} }(v_r)_ {max} $$
しかし、iの値を見つけるのは難しい作業です。の値に特定の制約を課すことができますiトランジット方式を使用します。星と地球の間の惑星の通過はトランジットと呼ばれます。トランジットを観測することで光度曲線を得ることができ、観測された光度曲線のフラックスの大幅な低下は、iが90度に近いことを意味します。そのような条件が満たされない場合、私たちはの価値について何も知ることができませんi。次に、の値mp それが実際にあるので、私たちが見つけたものは惑星の質量の下限として役立つことができます mp sin(i) そして sin(i) ≤ 1。
結論として、視線速度はいつでも測定できるが、トランジット測定はトランジット中にのみ行うことができ、長くは続かない可能性があるため、ラジアル速度法はトランジット法よりも便利です。
覚えておくべきポイント
惑星の軌道傾斜角を見つけることは、視線速度法では達成されません。
視線速度はトランジットとは異なり常に測定できるため、視線速度法はトランジット法よりも優れています。
トランジットは短命で、見逃しがちです。
トランジット方式 (Kepler Space Telescope)サイズを調べるために使用されます。惑星による星の明るさの低下は、通常、連星システムとは異なり、非常に少ないです。
F0 惑星がそれを食い止める前の星のフラックスです。
F1 惑星全体が星の前にあった後のフラックスです。
次の画像は、すべての計算に使用されます。

$$ \ frac {F_0 --F_1} {F_0} = \ frac {\ pi r_p ^ {2}} {\ pi R ^ 2_ \ ast} $$
$$ \ frac {\ Delta F} {F} \ cong \ frac {r ^ 2_p} {R ^ 2_ \ ast} $$
$$ \ left(\ frac {\ Delta F} {F} \ right)_ {earth} \ cong 0.001 \%$$
$$ \ left(\ frac {\ Delta F} {F} \ right)_ {jupiter} \ cong 1 \%$$
これは地上望遠鏡では簡単に実現できません。それはハッブル望遠鏡によって達成されます。

ここで、$ t_T $は位置AとDの間の時間であり、$ t_F $は位置BとCの間の時間です。
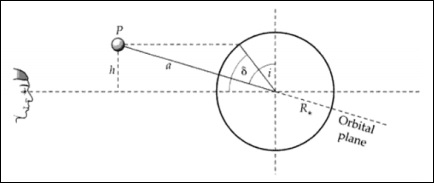
傾斜に関連するトランジットのジオメトリ iシステムの。トランジットの緯度と傾斜は交換可能です。
上記の画像から、次のように書くことができます。
$$ \ frac {h} {a} = cos(i)$$
$$ \ frac {h} {R_ \ ast} = sin(\ delta)$$
$$ cos(i)= \ frac {R_ \ ast sin(\ delta)} {a} $$
$$ y ^ 2 =(R_ \ ast + R_p)^ 2-h ^ 2 $$
$$ y = [(R_ \ ast + R_p)^ 2-h ^ 2] ^ {\ frac {1} {2}} $$
$$ sin(\ theta)= \ frac {y} {a} $$
$$ \ theta = sin ^ {-1} \ left [\ frac {(R_ \ ast + R_p)^ 2-a ^ 2cos ^ 2(i)} {a ^ 2} \ right] ^ {\ frac {1 } {2}} $$
$$ t_T = \ frac {P} {2 \ pi} \ times 2 \ theta $$
ここで、$ t_T $はトランジットが発生する期間の割合であり、(2θ/2π)はトランジットが発生する角度の割合です。
$$ sin(\ frac {t_T \ pi} {P})= \ frac {R_ \ ast} {a} \ left [\ left(1+ \ frac {R_p} {R_ \ ast} \ right)^ 2- \ left(\ frac {a} {R_ \ ast} cos(i)\ right)^ 2 \ right] ^ {\ frac {1} {2}} $$
通常、>> R ∗ >> Rp。だから、私たちは書くことができます-
$$ sin(\ frac {t_T \ pi} {P})= \ frac {R_ \ ast} {a} \ left [1- \ left(\ frac {a} {R_ \ ast} cos(i)\ right )^ 2 \ right] ^ {\ frac {1} {2}} $$
ここに、 P2つの連続するトランジット間の期間です。通過時間は、軌道期間と比較して非常に短いです。したがって、
$$ t_T = \ frac {P} {\ pi} \ left [\ left(\ frac {R_ \ ast} {a} \ right)^ 2-cos ^ 2(i)\ right] ^ {\ frac {1 } {2}} $$
ここに、 tT, P, R∗ オブザーバブルです、 a そして i 見つける必要があります。
さて、
$$ sin(\ frac {t_F \ pi} {P})= \ frac {R_ \ ast} {a} \ left [\ left(1- \ frac {R_p} {R_ \ ast} \ right)^ 2- \ left(\ frac {a} {R_ \ ast} cos \:i \ right)^ 2 \ right] ^ {\ frac {1} {2}} $$
ここで、$ y ^ 2 =(R_ \ ast − R_p)^ 2 − h ^ 2 $。
しましょう、
$$ \ frac {\ Delta F} {F} = D = \ left(\ frac {R_p} {R_ \ ast} \ right)^ 2 $$
今、私たちは表現することができます、
$$ \ frac {a} {R_ \ ast} = \ frac {2P} {\ pi} D ^ {\ frac {1} {4}}(t ^ 2_T-t ^ 2_F)^ {-\ frac {1 } {2}} $$
主系列星については、
$$ R_ \ ast \ propto M ^ \ alpha_ \ ast $$
$$ \ frac {R_ \ ast} {R_0} \ propto \ left(\ frac {M_ \ ast} {M_0} \ right)^ \ alpha $$
これは与える R∗。
したがって、「a」の値も取得します。
したがって、「R p」、「ap」、さらには「i」を取得します。
このすべてのために、
$$ h \ leq R_ \ ast + R_p $$
$$ a \:cos \:i \ leq R_ \ ast + R_p $$
〜89度でも、通過時間は非常に短いです。十分な通過時間を得るには、惑星が非常に接近している必要があります。これにより、「i」に厳しい制約が与えられます。'i'を取得すると、視線速度測定から'm p 'を導出できます。
トランジット法によるこの検出は、チャンス検出、つまりトランジットを観測する確率と呼ばれます。通過確率(観測確率)の計算を以下に示します。
通過確率は、2つの極端な通過構成によってトレースされた立体角に関連しています。
$$ Solid \:angle \:of \:planet \:= 2 \ pi \ left(\ frac {2R_ \ ast} {a} \ right)$$
半主軸a、または-での全立体角と同様に
$$ Solid \:angle \:of \:sphere \:= \:4 \ pi $$
確率は、これら2つの領域の比率です-
$$ = \:\ frac {area \:of \:sky \:covered \:by \:favorite \:orientation} {area \:of \:sky \:covered \:by \:all \:possible \:方向\:of \:軌道} $$
$ = \ frac {4 \ pi a_pR_ \ ast} {4 \ pi a ^ 2_p} = \ frac {R_ \ ast} {a_p} $ $ \ frac {area \:of \:hollow \:cyclinder} {area \ :of \:sphere} $
この確率は、オブザーバーとは無関係です。
覚えておくべきポイント
- トランジット法(ケプラー宇宙望遠鏡)を使用してサイズを調べます。
- トランジット法による検出は偶然の検出です。
- 十分な通過時間を得るには、惑星が非常に接近している必要があります。
- 通過確率は惑星の立体角に関係しています。
- この確率は、オブザーバーの基準系とは無関係です。
2004年の太陽系外惑星の最初の直接画像は、質量の惑星でした。 3-10 Mjupiter 褐色矮星(2M1207)の周りを周回し、質量は 25 Mjupiter。視線速度、トランジット、重力マイクロレンズ法、イメージング、位置天文学などの技術は、太陽系外惑星の検出に使用されてきました。検出数は年々増加しています。
2010年頃までは視線速度法が広く使われていましたが、今ではほとんどの検出がトランジット法で行われています。2014年には、検出数が急増しました。Kepler Space Telescope (KST) 結果を出し始めました。
質量周期分布は、視線速度法がより大きな周期の巨大惑星の検出に偏っていることを示していますが、トランジット法を使用すると、次の画像に示すように、より低い周期の惑星のみが検出されます(提供:NASA太陽系外惑星アーカイブ) 。
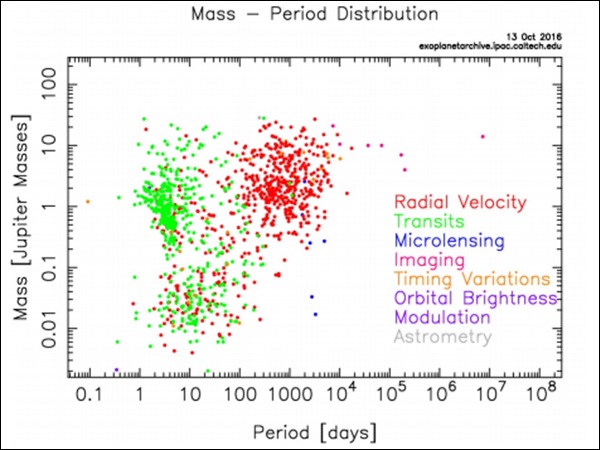
KSTの出現以来、より小さな質量の惑星の検出数が大幅に増加しています。これは、以下の図から明らかです。KSTによって検出された惑星は、「ホットジュピター」と呼ばれる高温の大質量惑星と、「ホットスーパーアース」と呼ばれる低質量の惑星(地球よりも質量が大きいため)の2つのグループに分けられます。

検出された太陽系外惑星の数とそれらまでの距離をプロットすると、これらの惑星のほとんどが2kpc以内にあり、これは私たちの銀河内に十分にあります。私たちの検出は宇宙のごく一部にある特定の種類の惑星だけに限定されているので、おそらく惑星は宇宙ではそれほど珍しいことではありません。
惑星はから形成されます circumstellar disc または proto planetary disc。星形成の際に副産物として惑星が形成された場合、宇宙の惑星数が宇宙の星数を超えているのではないでしょうか!
ハビタブルゾーン
ハビタブルゾーンは、水が液体の形で存在できる星の周りのゾーンとして定義できます。次の図に示すように、星から$ a_p $の距離にある惑星について考えてみます。惑星の温度を計算する簡単な方法は次のとおりです。
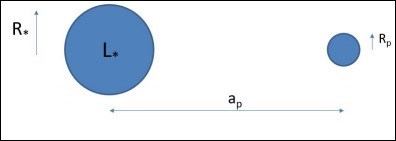
$$ \ left(\ frac {L_ \ ast} {4 \ pi a ^ 2_p} \ right)\ pi R ^ 2_p(1-A)= 4 \ pi R ^ 2_p \ sigma T ^ 4_p $$
そして
$$ \ frac {L_ \ ast} {4 \ pi R ^ 2_ \ ast} = \ sigma T ^ 4_ \ ast $$
$$ \したがって、T_p =(1-A)T_ \ ast \ sqrt {\ frac {R_ \ ast} {2a_p}} $$
私たちの場合、
Lsun = 3.83 x 1026
ap = 1.5 ∗ 1011 and
A = 0.3
$ T_ {Earth} = 255K $になります。雲物理学を含む実際の計算は非常に複雑です。私たちの太陽系のハビタブルゾーンは0.9AUから1.7AUの間にあります。
太陽の光度は、ガス圧が低下するため、時間とともに増加することがわかりました。水素を燃やし始めたときは30%明るさが弱かった。これにより、ハビタブルゾーンが太陽から遠ざかります。地球はハビタブルゾーンの内側の端に近いので、いつかゾーンの外に移動するかもしれません!
継続的に居住可能なゾーン
要するにそれはとして呼ばれます CHZ星の主系列星の全寿命にわたって液体の水が存在できる領域として定義できます。KSTは、ハビタブルゾーンにある多くの太陽系外惑星を検出しました。
生命存在指標とは、元素、同位体、分子、現象など、過去または現在の生命の科学的証拠を提供するあらゆる物質です。例では、Oの両方の検出である2とCO 2のみ地質工程を経て、通常は不可能である惑星、オン。この検出は、吸収スペクトルを分析することによって行われます。
覚えておくべきポイント
視線速度、トランジット、重力マイクロレンズ法、イメージング、位置天文学などの技術は、太陽系外惑星の検出に使用されてきました。
視線速度法は、周期の長い巨大な惑星の検出に偏っています。
高温の大惑星は「ホットジュピター」と呼ばれ、低質量の惑星は「ホットスーパーアース」と呼ばれます。
宇宙の惑星の数は、宇宙の星の数を超えています。
ハビタブルゾーンは、水が液体の形で存在できる星の周りのゾーンとして定義できます。