宇宙論-ロバートソン-ウォーカーメートル法
この章では、Robertson-Walkerメトリックについて詳しく説明します。
時間とともに変化するスケールファクターのモデル
遠方の銀河から光子が放出されたとしましょう。スペースはすべての方向のフォトンのために前方にあります。宇宙の膨張はあらゆる方向にあります。次の手順で、スケール係数が時間とともにどのように変化するかを見てみましょう。
Step 1 −静的宇宙の場合、スケール係数は1です。つまり、共動距離の値はオブジェクト間の距離です。
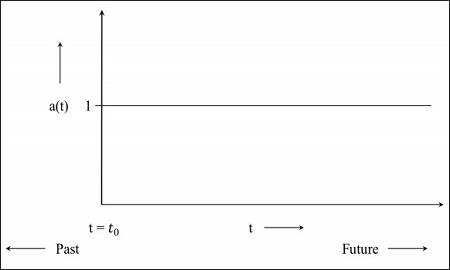
Step 2−次の画像は、まだ拡大しているが速度が減少している宇宙のグラフです。これは、グラフが過去に開始されることを意味します。ザ・t = 0 宇宙がその時点から始まったことを示します。

Step 3 −次の画像は、より速い速度で拡大している宇宙のグラフです。

Step 4 −次の画像は、これから収縮し始める宇宙のグラフです。

スケールファクターの値が 0 宇宙の収縮の間に、それはオブジェクト間の距離が 0、つまり適切な距離は次のようになります 0。現在の宇宙の物体間の距離である共動距離は一定量です。将来、スケールファクターが0、すべてが近づきます。モデルは宇宙の構成要素に依存します。
平らな(ユークリッド:曲率のパラメーターはありません)膨張宇宙のメトリックは、次のように与えられます。
$$ ds ^ 2 = a ^ 2(t)\ left(dr ^ 2 + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2 \ right)$$
時空の場合、上記の式で得られた線要素は次のように変更されます。
$$ ds ^ 2 = c ^ 2dt ^ 2- \ left \ {a ^ 2(t)\ left(dr ^ 2 + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2 \右)\ right \} $$
時空の場合、光子が放出される時間と検出される時間は異なります。適切な距離は、宇宙の膨張によって時間とともに変化する可能性のあるオブジェクトまでの瞬間的な距離です。これは、フォトンがさまざまなオブジェクトから移動して私たちに到達した距離です。これは、共動距離に次のように関係しています。
$$ d_p = a(t)\ times d_c $$
ここで、$ d_p $は適切な距離であり、$ d_c $は固定されている共動距離です。
現在の宇宙の物体まで測定された距離は共動距離と見なされます。つまり、共動距離は固定されており、拡張によって変化しません。以前は、スケール係数は1未満でした。これは、適切な距離が小さかったことを示しています。
銀河への赤方偏移を測定することができます。したがって、適切な距離$ d_p $は$ c \ times t(z)$に対応します。ここで、$ t(z)$は赤方偏移へのルックバック時間であり、cは真空中の光速です。ルックバック時間は赤方偏移の関数です(z)。
上記の概念に基づいて、$ d_p = a(t)\ times d_c $のこのシナリオで宇宙論的赤方偏移がどのように解釈されるかを分析しましょう。
光子(地球に結合している)が銀河Gによって放出されたと仮定します。$ t_ {em} $は、光子が放出された時間に対応します。$ a(t_ {em})$は、フォトンが放出されたときのスケールファクターでした。光子の検出時までに、宇宙全体が拡大しました。つまり、光子は検出時に赤方偏移します。$ t_ {obs} $は、光子が検出された時間に対応し、対応するスケール係数は$ a(t_ {obs})$です。
宇宙が成長した要因は次の式で与えられます-
$$ \ frac {a(t_ {obs})} {a(t_ {em})} $$
波長が拡大した要因は−
$$ \ frac {\ lambda_ {obs}} {\ lambda_ {em}} $$
これは宇宙が成長した要因に等しいです。記号には通常の意味があります。したがって、
$$ \ frac {a(t_ {obs})} {a(t_ {em})} = \ frac {\ lambda_ {obs}} {\ lambda_ {em}} $$
私たちはその赤方偏移を知っています (z) は−
$$ z = \ frac {\ lambda_ {obs}-\ lambda_ {em}} {\ lambda_ {em}} = \ frac {\ lambda_ {obs}} {\ lambda_ {em}}-1 $$
$$ 1 + z = \ frac {a(t_ {obs})} {a(t_ {em})} $$
スケールファクターの現在の値は1であるため、$ a(t_ {obs})= 1 $であり、過去に$ a(t)$によってフォトンが放出されたときのスケールファクターを示します。
したがって、
$$ 1 + z = \ frac {1} {a(t)} $$
宇宙論における赤方偏移の解釈
これを理解するために、次の例を見てみましょう。$ z = 2 $の場合、$ a(t)= 1/3 $です。
これは、光がその物体を離れてから、宇宙が3倍に拡大したことを意味します。放射物体からの通過中に空間が同じ係数で拡大したため、受信した放射線の波長は3倍に拡大しました。このような大きな値では、z、赤方偏移は主に宇宙論的赤方偏移であり、私たちに対するオブジェクトの実際の後退速度の有効な尺度ではありません。
宇宙マイクロ波背景放射(CMB)の場合、 z = 1089、これは、現在の宇宙が次の係数で拡大したことを意味します ∼1090。平らなユークリッド膨張宇宙の計量は次のように与えられます-
$$ ds ^ 2 = a ^ 2(t)(dr ^ 2 + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2)$$
メトリックを任意の曲率で記述したいと思います。
Robertson and Walker 曲率ユニバース(均一で等方性)で証明された場合、メトリックは次のように与えられます。
$$ ds ^ 2 = a ^ 2(t)\ left [\ frac {dr ^ 2} {1-kr ^ 2} + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2 \ right] $$
これは一般的に知られています Robertson–Walker Metricそして、空間のあらゆるトポロジーに当てはまります。$ dr ^ 2 $の余分な要素に注意してください。ここに は曲率定数です。
宇宙の形
宇宙の形は、次の曲率の助けを借りて説明されています。
- 正の曲率
- 負の曲率
- 曲率ゼロ
これらのそれぞれを詳細に理解しましょう。
正の曲率
曲率のサーフェス上の任意のポイントで描画された接平面がサーフェス上のどのポイントでも交差しない場合、それは正の曲率を持つサーフェスと呼ばれます。つまり、サーフェスはそのポイントで接平面の片側に留まります。球の表面は正の曲率を持っています。
負の曲率
曲率の表面上の点に描かれた接平面が表面上の任意の点で交差する場合、それは負の曲率を持つ表面と呼ばれます。つまり、表面は2つの異なる方向に接平面から離れて湾曲します。鞍型の表面は負の曲率を持っています。
次に、球の表面について考えます。3点を測地線(大円の弧)で結合して球の表面に三角形を作成すると、球面三角形の内角の合計は180 oを超えます。つまり、−
$$ \ alpha + \ beta + \ gamma> \ pi $$
このような空間は、正に湾曲した空間と呼ばれます。また、曲率は均一で等方性です。一般に、球面三角形の頂点での角度は、次の関係に従います。
$$ \ alpha + \ beta + \ gamma = \ pi + A / R ^ 2 $$
どこ A は三角形の面積であり、 Rは球の半径です。次の画像は、正に湾曲した空間を示しています。

正の曲率の場合、平行線は一致する必要があります。正に湾曲した空間である地球の表面を考えてみましょう。赤道上の2つの開始点を取ります。赤道を直角に横切る線は経度線として知られています。これらの線は赤道と直角に交差するため、平行線と呼ぶことができます。赤道から始まり、最終的には極で交差します。この方法はによって使用されましたCarl Gauss と他の人は地球のトポロジーを理解します。
負考える-湾曲した空間(以下の図に示すサドル)を、内部の和は三角形の角度が180°未満であるOすなわち、 -
$$ \ alpha + \ beta + \ gamma <\ pi $$
頂点の角度は次の関係に従います-
$$ \ alpha + \ beta + \ gamma = \ pi-A / R ^ 2 $$

曲率ゼロ
平面の曲率はゼロです。ここで、平坦な空間の場合、平面を取り、3つの点を測地線(直線)で結合して三角形を作成すると、内部の角度の合計は次のようになります。
$$ \ alpha + \ beta + \ gamma = \ pi $$
次の画像は平らな2次元空間です。

空間を均一で等方性にしたい場合は、3つの可能性のみが残ります。空間を均一に平坦にするか、均一な正の曲率にするか、均一な負の曲率にするかです。
曲率定数は、次の3つの値のいずれかをとることができます。
$$ k = \ begin {cases} + 1、&for \:a \:positive \:curved \:space; \\\ quad 0、&for \:a \:flat \:space; \\-1 &for \:a \:負に\:湾曲\:スペース; \ end {cases} $$
宇宙のグローバルトポロジー
宇宙には特定のトポロジーがありますが、局所的にはしわがある可能性があります。物質が空間にどのように分布しているかに応じて、曲率の変化は小さくなります。宇宙のどこにいても同じ真のサイズを持つオブジェクトのクラスがあると仮定しましょう。つまり、それらは標準のキャンドルのようなものです。それらは同じ明るさではありませんが、同じサイズです。
オブジェクトが正に湾曲した空間にあり、光子が点A(オブジェクトの一方の端)とB(オブジェクトのもう一方の端)から来る場合、光子は測地線のパスを介して正に湾曲した空間で平行に伝播し、最終的に合流します。Cの観測者にとって、それは異なる方向の2つの異なる点から来たように見えます。
オブジェクトがローカルユニバースにあり、角度サイズを測定する場合、曲率の影響を受けません。同じクラスのオブジェクトがより大きな赤方偏移で見られる場合、角度サイズはと相関しません。
$$ \ theta = \ frac {d} {r} $$
どこ d オブジェクトのサイズであり、 rはオブジェクトまでの距離です。つまり、サイズがローカルサイズよりも大きい場合は、曲率が正であることを意味します。次の画像は、正に湾曲した空間で検出された光子を表したものです。

標準的なサイズと形態の実際の天体物理学的オブジェクトは存在しないことに注意してください。巨大な楕円形のcD–銀河は標準的なろうそくに合うと考えられていましたが、時間とともに進化していることもわかりました。
銀河までの距離を見つける
このセクションでは、次の画像を考慮して、銀河までの距離を見つける方法について説明します。

宇宙論的な休息フレームの(r、θ、)での天の川を考えてみましょう。= 0を取ることができます。(0、θ、ϕ)、つまり、均質性の仮定を呼び出すことによる宇宙の中心。
(r1、θ、)にある銀河「G」を考えてみましょう。距離(適切)は、光子が移動する最短の半径距離です。時空の対称性から、r = 0からr = r1までのヌル測地線は、空間内で一定の方向を持っています。その半径方向の伝搬では、角度座標は変化しません。角度座標が変更された場合、それは最短経路ではありません。これは、曲率項がDRに存在している理由である2。
覚えておくべきポイント
宇宙の膨張はあらゆる方向にあります。
宇宙は、スケールファクターの進化に応じて、静的、拡大、または縮小することができます。
cD銀河は時間とともに進化するため、標準光源として使用することはできません。
宇宙には特定のトポロジーがありますが、局所的にはしわがある可能性があります。