아날로그 통신-각도 변조
연속파 변조에서 다른 유형의 변조는 Angle Modulation. 각도 변조는 반송파 신호의 주파수 또는 위상이 메시지 신호에 따라 달라지는 프로세스입니다.
각도 변조 파의 표준 방정식은 다음과 같습니다.
$$ s \ left (t \ right) = A_c \ cos \ theta _i \ left (t \ right) $$
어디,
$ A_c $는 변조 파의 진폭으로 반송파 신호의 진폭과 동일합니다.
$ \ theta _i \ left (t \ right) $는 변조 된 파동의 각도입니다.
각도 변조는 주파수 변조와 위상 변조로 더 나뉩니다.
Frequency Modulation 메시지 신호와 함께 반송파 신호의 주파수를 선형으로 변경하는 프로세스입니다.
Phase Modulation 메시지 신호와 함께 반송파 신호의 위상을 선형으로 변경하는 프로세스입니다.
이제 이에 대해 자세히 논의하겠습니다.
주파수 변조
진폭 변조에서 반송파 신호의 진폭은 다양합니다. 반면에Frequency Modulation (FM), 반송파 신호의 주파수는 변조 신호의 순간 진폭에 따라 달라집니다.
따라서 주파수 변조에서 반송파 신호의 진폭과 위상은 일정하게 유지됩니다. 이것은 다음 그림을 보면 더 잘 이해할 수 있습니다.


변조 또는 메시지 신호의 진폭이 증가하면 변조 파의 주파수가 증가합니다. 마찬가지로 변조 신호의 진폭이 감소하면 변조 파의 주파수가 감소합니다. 변조 신호의 진폭이 0 일 때 변조 파의 주파수는 일정하게 유지되고 반송파 신호의 주파수와 동일합니다.
수학적 표현
FM 변조에서 순간 주파수 $ f_i $에 대한 방정식은 다음과 같습니다.
$$ f_i = f_c + k_fm \ 왼쪽 (t \ 오른쪽) $$
어디,
$ f_c $는 반송파 주파수입니다.
$ k_t $는 주파수 민감도입니다.
$ m \ left (t \ right) $는 메시지 신호입니다.
각 주파수 $ \ omega_i $와 각도 $ \ theta _i \ left (t \ right) $ 사이의 관계를 알고 있습니다.
$$ \ omega_i = \ frac {d \ theta _i \ left (t \ right)} {dt} $$
$ \ Rightarrow 2 \ pi f_i = \ frac {d \ theta _i \ left (t \ right)} {dt} $
$ \ Rightarrow \ theta _i \ left (t \ right) = 2 \ pi \ int f_i dt $
위 방정식에서 $ f_i $ 값을 대입합니다.
$$ \ theta _i \ left (t \ right) = 2 \ pi \ int \ left (f_c + k_f m \ left (t \ right) \ right) dt $$
$ \ Rightarrow \ theta _i \ left (t \ right) = 2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt $
각도 변조 파의 표준 방정식에서 $ \ theta _i \ left (t \ right) $ 값을 대입합니다.
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt \ right) $$
이것이 equation of FM wave.
변조 신호가 $ m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right) $이면 FM 파의 방정식은 다음과 같습니다.
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ beta \ sin \ left (2 \ pi f_mt \ right) \ right) $$
어디,
$ \ 베타 $ = modulation index $ = \ frac {\ Delta f} {f_m} = \ frac {k_fA_m} {f_m} $
FM 변조 주파수 (순간 주파수)와 일반 반송파 주파수의 차이는 다음과 같습니다. Frequency Deviation. $ \ Delta f $로 표시되며 $ k_f $ 및 $ A_m $의 곱과 같습니다.
FM은 다음과 같이 나눌 수 있습니다. Narrowband FM 과 Wideband FM 변조 지수 $ \ beta $의 값을 기반으로합니다.
협 대역 FM
다음은 협 대역 FM의 기능입니다.
이 주파수 변조는 광대역 FM에 비해 대역폭이 작습니다.
변조 지수 $ \ beta $는 작습니다. 즉, 1보다 작습니다.
스펙트럼은 반송파, 상부 측 파대 및 하부 측 파대로 구성됩니다.
이것은 경찰 무선, 구급차, 택시 등과 같은 이동 통신에 사용됩니다.
광대역 FM
다음은 Wideband FM의 기능입니다.
이 주파수 변조에는 무한한 대역폭이 있습니다.
변조 지수 $ \ beta $는 1보다 큽니다.
스펙트럼은 반송파와 주변에 위치한 무한한 수의 측 파대로 구성됩니다.
이것은 FM 라디오, TV 등과 같은 엔터테인먼트, 방송 응용 프로그램에 사용됩니다.
위상 변조
주파수 변조에서 반송파의 주파수는 다양합니다. 반면에Phase Modulation (PM), 반송파 신호의 위상은 변조 신호의 순간 진폭에 따라 달라집니다.
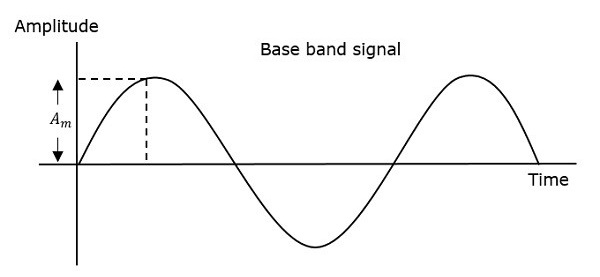
따라서 위상 변조에서 반송파 신호의 진폭과 주파수는 일정하게 유지됩니다. 이것은 다음 그림을 보면 더 잘 이해할 수 있습니다.
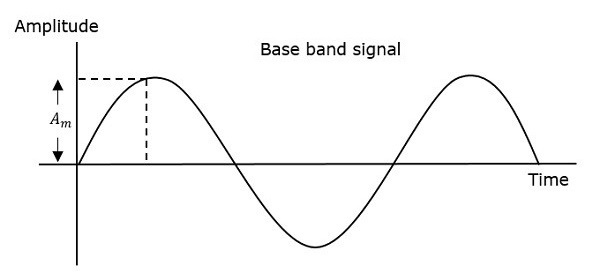

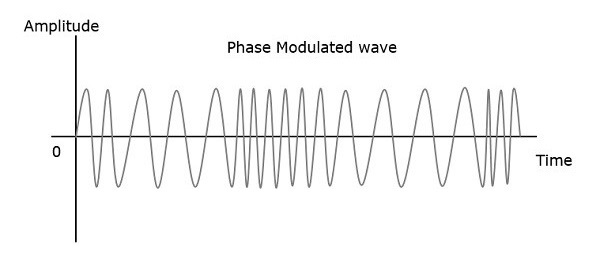
변조 된 파동의 위상에는 파동의 위상 변화가 발생할 수있는 무한 지점이 있습니다. 변조 신호의 순간 진폭은 반송파 신호의 위상을 변경합니다. 진폭이 양수이면 위상이 한 방향으로 변경되고 진폭이 음수이면 위상이 반대 방향으로 변경됩니다.
수학적 표현
위상 변조에서 순간 위상 $ \ phi_i $의 방정식은 다음과 같습니다.
$$ \ phi _i = k_p m \ left (t \ right) $$
어디,
$ k_p $는 위상 감도입니다.
$ m \ left (t \ right) $는 메시지 신호입니다.
각도 변조 파의 표준 방정식은 다음과 같습니다.
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ phi_i \ right) $$
위 방정식에서 $ \ phi_i $ 값을 대입합니다.
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + k_p m \ left (t \ right) \ right) $$
이것이 equation of PM wave.
변조 신호 $ m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right) $, PM 파의 방정식은 다음과 같습니다.
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ beta \ cos \ left (2 \ pi f_mt \ right) \ right) $$
어디,
$ \ 베타 $ = modulation index = $ \ 델타 \ phi = k_pA_m $
$ \ Delta \ phi $는 위상 편차입니다.
위상 변조는 이동 통신 시스템에 사용되며 주파수 변조는 주로 FM 방송에 사용됩니다.