아날로그 통신-퀵 가이드
의사 소통이라는 단어는 "공유하다"를 의미하는 라틴어 commūnicāre에서 유래했습니다. 의사 소통은 정보 교환의 기본 단계입니다.
예를 들어, 요람에있는 아기는 어머니가 필요할 때 울면서 의사 소통을합니다. 소는 위험에 처했을 때 큰 소리로 울부 짖습니다. 사람은 언어의 도움으로 의사 소통합니다. 의사 소통은 공유하는 다리입니다.
Communication 두 명 이상의 개인간에 말, 행동, 기호 등과 같은 수단을 통해 정보를 교환하는 과정으로 정의 할 수 있습니다.
통신 시스템의 일부
통신을 제공하는 모든 시스템은 다음 그림과 같이 세 가지 중요하고 기본적인 부분으로 구성됩니다.

Sender메시지를 보내는 사람입니다. 신호가 전송되는 전송 스테이션 일 수 있습니다.
Channel 메시지 신호가 목적지에 도달하기 위해 이동하는 매체입니다.
Receiver메시지를받는 사람입니다. 전송 된 신호가 수신되는 수신 스테이션 일 수 있습니다.
신호 유형
제스처, 소리, 행동 등과 같은 수단으로 정보를 전달하는 것은 다음과 같이 불릴 수 있습니다. signaling. 따라서 신호는 일부 정보를 전송하는 에너지 원이 될 수 있습니다. 이 신호는 발신자와 수신자 간의 통신을 설정하는 데 도움이됩니다.
메시지를 전달하기 위해 거리를 이동하는 전기 충격 또는 전자기파는 signal 통신 시스템에서.
신호는 특성에 따라 주로 아날로그와 디지털의 두 가지 유형으로 분류됩니다. 아날로그 및 디지털 신호는 다음 그림과 같이 추가로 분류됩니다.

아날로그 신호
시간이 변하는 양을 나타내는 연속적인 시변 신호는 다음과 같이 불릴 수 있습니다. Analog Signal. 이 신호는 그것을 나타내는 수량의 순간 값에 따라 시간에 따라 계속 변합니다.
예
한 시간 (오전 6 시부 터 오전 7 시까 지)에 100 리터 용량의 탱크를 채우는 수도꼭지를 고려해 보겠습니다. 탱크를 채우는 부분은 시간에 따라 달라집니다. 즉, 15 분 (6:15 AM) 후에 탱크의 1/4 부분이 채워지는 반면 6:45 AM에는 탱크의 3/4가 채워집니다.
변화하는 시간에 따라 탱크의 물의 변화하는 부분을 플롯하려고하면 다음 그림과 같습니다.

이 이미지에 표시된 결과는 시간에 따라 달라 지므로 (증가) time varying quantity아날로그 수량으로 이해할 수 있습니다. 그림에서 기울어 진 선으로이 상태를 나타내는 신호는Analog Signal. 아날로그 신호 및 아날로그 값을 기반으로 한 통신을 다음과 같이 호출합니다.Analog Communication.
디지털 신호
본질적으로 불연속 적이거나 형태가 비 연속적인 신호는 Digital signal. 이 신호에는 개별 값이 있으며, 개별 값은 특정 시점에서 파생 된 것처럼 이전 값을 기반으로하지 않습니다.
예
20 명의 학생이있는 교실을 생각해 봅시다. 1 주일 출석을 표시하면 다음 그림과 같습니다.

이 그림에서 값은 별도로 표시됩니다. 예를 들어 수요일 수업 출석률은 20 명이고 토요일은 15 명입니다. 이러한 값은 개별적으로 또는 개별적으로 고려 될 수 있으므로 다음과 같이 호출됩니다.discrete values.
1과 0 만있는 이진수는 대부분 digital values. 따라서 1과 0을 나타내는 신호는digital signals. 디지털 신호와 디지털 값을 기반으로 한 통신을Digital Communication.
주기적 신호
일정 기간 동안 패턴을 반복하는 아날로그 또는 디지털 신호를 Periodic Signal. 이 신호는 패턴이 반복적으로 계속되고 가정하거나 계산하기 쉽습니다.
예
산업에서 기계를 고려한다면, 차례로 일어나는 과정은 연속적인 절차입니다. 예를 들어, 원자재 조달 및 등급 지정, 일괄 처리, 제품로드 포장 등은 특정 절차를 반복적으로 따릅니다.
아날로그 또는 디지털로 간주되는 이러한 프로세스는 다음과 같이 그래픽으로 나타낼 수 있습니다.

비 주기적 신호
일정 기간 동안 패턴을 반복하지 않는 아날로그 또는 디지털 신호를 Aperiodic Signal. 이 신호는 패턴이 계속되지만 패턴이 반복되지 않습니다. 가정하거나 계산하는 것도 그리 쉽지 않습니다.
예
사람의 일상은 고려할 경우 다양한 작업에 대해 서로 다른 시간 간격을 사용하는 다양한 유형의 작업으로 구성됩니다. 시간 간격이나 작업이 계속 반복되지 않습니다. 예를 들어, 한 사람은 아침부터 밤까지 계속해서 양치질하지 않을 것입니다.
아날로그 또는 디지털로 간주되는 이러한 프로세스는 다음과 같이 그래픽으로 나타낼 수 있습니다.


일반적으로 통신 시스템에서 사용되는 신호는 본질적으로 아날로그이며, 아날로그로 전송되거나 디지털로 변환 된 후 요구 사항에 따라 전송됩니다.
외부 간섭이나 노이즈 추가의 영향없이 희미 해지지 않고 멀리 떨어진 신호를 전송하려면 다음과 같은 프로세스를 거쳐야합니다. Modulation. 원래 신호의 매개 변수를 방해하지 않고 신호의 강도를 향상시킵니다.
변조 란?
신호를 전달하는 메시지는 멀리서 전송되어야하며 안정적인 통신을 설정하려면 메시지 신호의 원래 특성에 영향을주지 않는 고주파 신호의 도움을 받아야합니다.
메시지 신호의 특성이 변경되면 포함 된 메시지도 변경됩니다. 따라서 메시지 신호를 처리하는 것이 필수입니다. 고주파 신호는 외부 방해의 영향을받지 않고 먼 거리까지 이동할 수 있습니다. 우리는 이러한 고주파 신호의 도움을받습니다.carrier signal메시지 신호를 전송합니다. 이러한 프로세스를 단순히 변조라고합니다.
변조는 변조 신호의 순간 값에 따라 반송파 신호의 매개 변수를 변경하는 프로세스입니다.
변조의 필요성
베이스 밴드 신호는 직접 전송과 호환되지 않습니다. 이러한 신호의 경우 더 먼 거리를 이동하려면 변조 신호의 매개 변수에 영향을주지 않는 고주파 반송파로 변조하여 강도를 높여야합니다.
변조의 장점
전송에 사용되는 안테나는 변조가 도입되지 않은 경우 매우 커야했습니다. 파도가 왜곡되지 않고 멀리 이동할 수 없기 때문에 통신 범위가 제한됩니다.
다음은 통신 시스템에서 변조를 구현하는 몇 가지 장점입니다.
- 안테나 크기 감소
- 신호 혼합 없음
- 통신 범위 증가
- 신호 다중화
- 대역폭 조정 가능성
- 수신 품질 향상
변조 프로세스의 신호
다음은 변조 프로세스의 세 가지 신호 유형입니다.
메시지 또는 변조 신호
전송할 메시지가 포함 된 신호를 message signal. 변조 과정을 거쳐야 전송되는 기저 대역 신호입니다. 따라서 그것은 또한modulating signal.
캐리어 신호
특정 진폭, 주파수 및 위상을 갖지만 정보를 포함하지 않는 고주파 신호를 carrier signal. 빈 신호이며 변조 후 신호를 수신기로 전달하는 데 사용됩니다.
변조 된 신호
변조 과정 후의 결과 신호를 modulated signal. 이 신호는 변조 신호와 반송파 신호의 조합입니다.
변조 유형
변조에는 여러 유형이 있습니다. 사용되는 변조 기술에 따라 다음 그림과 같이 분류됩니다.

변조 유형은 크게 연속파 변조와 펄스 변조로 분류됩니다.
연속파 변조
연속파 변조에서는 고주파 사인파가 반송파로 사용됩니다. 이것은 진폭과 각도 변조로 더 나뉩니다.
고주파 반송파의 진폭이 변조 신호의 순간 진폭에 따라 변하면 이러한 기술을 다음과 같이 호출합니다. Amplitude Modulation.
변조 신호의 순간 값에 따라 반송파의 각도가 변하면 이러한 기술을 다음과 같이 호출합니다. Angle Modulation. 각도 변조는 주파수 변조와 위상 변조로 더 나뉩니다.
변조 신호의 순간 값에 따라 반송파의 주파수가 변하면 이러한 기술을 다음과 같이 호출합니다. Frequency Modulation.
고주파 반송파의 위상이 변조 신호의 순간 값에 따라 변하면 이러한 기술을 다음과 같이 호출합니다. Phase Modulation.
펄스 변조
펄스 변조에서는 직사각형 펄스의 주기적 시퀀스가 반송파로 사용됩니다. 이것은 아날로그 및 디지털 변조로 더 나뉩니다.
아날로그 변조 기술에서 펄스의 진폭 또는 지속 시간 또는 위치가 기저 대역 변조 신호의 순간 값에 따라 변경되는 경우 이러한 기술을 PAM (Pulse Amplitude Modulation) 또는 PDM (Pulse Duration / Width Modulation)이라고합니다. / PWM) 또는 PPM (Pulse Position Modulation).
디지털 변조에서 사용되는 변조 기술은 아날로그 신호가 1과 0의 디지털 형태로 변환되는 PCM (Pulse Code Modulation)입니다. 그 결과 코딩 된 펄스 트레인이 생성되므로이를 PCM이라고합니다. 이것은 Delta Modulation (DM)으로 더욱 발전되었습니다. 이러한 디지털 변조 기술은 디지털 통신 자습서에서 설명합니다.
연속 파는 간격없이 연속적으로 진행되며 정보를 포함하는 기저 대역 메시지 신호입니다. 이 파동은 변조되어야합니다.
표준 정의에 따르면 "반송파 신호의 진폭은 변조 신호의 순간 진폭에 따라 달라집니다." 즉, 정보를 포함하지 않는 반송파 신호의 진폭은 정보를 포함하는 신호의 진폭에 따라 매 순간 변합니다. 이것은 다음 그림으로 잘 설명 될 수 있습니다.



첫 번째 그림은 메시지 신호 인 변조 파를 보여줍니다. 다음은 반송파로 고주파 신호이며 정보가 없습니다. 한편, 마지막 것은 결과 변조 파입니다.
반송파의 양의 피크와 음의 피크가 가상의 선과 상호 연결되어 있음을 알 수 있습니다. 이 라인은 변조 신호의 정확한 모양을 재현하는 데 도움이됩니다. 반송파의이 가상 선을Envelope. 메시지 신호와 동일합니다.
수학적 표현
다음은 이러한 파동에 대한 수학적 표현입니다.
파동의 시간 영역 표현
변조 신호는 다음과 같습니다.
$$ m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right) $$
반송파 신호는
$$ c \ 왼쪽 (t \ 오른쪽) = A_c \ cos \ 왼쪽 (2 \ pi f_ct \ 오른쪽) $$
어디,
$ A_m $ 및 $ A_c $는 각각 변조 신호와 반송파 신호의 진폭입니다.
$ f_m $ 및 $ f_c $는 각각 변조 신호와 반송파 신호의 주파수입니다.
그러면 진폭 변조 파의 방정식은 다음과 같습니다.
$ s (t) = \ left [A_c + A_m \ cos \ left (2 \ pi f_mt \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $ (수식 1)
변조 지수
반송파는 변조 된 후 변조 된 레벨이 계산되면 이러한 시도를 다음과 같이 호출합니다. Modulation Index 또는 Modulation Depth. 반송파가 겪는 변조 수준을 나타냅니다.
수식 1을 아래와 같이 다시 정렬합니다.
$ s (t) = A_c \ left [1+ \ left (\ frac {A_m} {A_c} \ right) \ cos \ left (2 \ pi f_mt \ right) \ right] \ cos \ left (2 \ pi f_ct \ 오른쪽) $
$ \ Rightarrow s \ left (t \ right) = A_c \ left [1 + \ mu \ cos \ left (2 \ pi f_m t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $ ( 방정식 2)
여기서 $ \ mu $는 변조 지수이며 $ A_m $와 $ A_c $의 비율과 같습니다. 수학적으로 다음과 같이 쓸 수 있습니다.
$ \ mu = \ frac {A_m} {A_c} $ (수식 3)
따라서 메시지 및 반송파 신호의 진폭을 알고있는 경우 위의 공식을 사용하여 변조 지수의 값을 계산할 수 있습니다.
이제 방정식 1을 고려하여 변조 지수에 대한 공식을 하나 더 유도 해 보겠습니다. 변조 된 파동의 최대 진폭과 최소 진폭을 알고있는 경우이 공식을 변조 지수 값을 계산하는 데 사용할 수 있습니다.
$ A_ \ max $ 및 $ A_ \ min $을 변조 파의 최대 및 최소 진폭이라고합니다.
$ \ cos \ left (2 \ pi f_mt \ right) $가 1 일 때 변조 된 파동의 최대 진폭을 얻습니다.
$ \ Rightarrow A_ \ max = A_c + A_m $ (수식 4)
$ \ cos \ left (2 \ pi f_mt \ right) $가 -1 일 때 변조 된 파동의 최소 진폭을 얻습니다.
$ \ Rightarrow A_ \ min = A_c-A_m $ (수식 5)
방정식 4와 방정식 5를 추가합니다.
$$ A_ \ 최대 + A_ \ min = A_c + A_m + A_c-A_m = 2A_c $$
$ \ Rightarrow A_c = \ frac {A_ \ max + A_ \ min} {2} $ (수식 6)
방정식 4에서 방정식 5를 뺍니다.
$$ A_ \ max-A_ \ min = A_c + A_m-\ left (A_c -A_m \ right) = 2A_m $$
$ \ Rightarrow A_m = \ frac {A_ \ max-A_ \ min} {2} $ (수식 7)
수학 식 7과 수학 식 6의 비율은 다음과 같다.
$$ \ frac {A_m} {A_c} = \ frac {\ left (A_ {max}-A_ {min} \ right) / 2} {\ left (A_ {max} + A_ {min} \ right) / 2 } $$
$ \ Rightarrow \ mu = \ frac {A_ \ max-A_ \ min} {A_ \ max + A_ \ min} $ (수식 8)
따라서 방정식 3과 방정식 8은 변조 지수에 대한 두 가지 공식입니다. 변조 지수 또는 변조 깊이는 종종 변 조율 (Percentage of Modulation)이라고하는 백분율로 표시됩니다. 우리는 얻을 것입니다percentage of modulation, 변조 인덱스 값에 100을 곱하면됩니다.
완벽한 변조를 위해서는 변조 인덱스 값이 1이어야하며 이는 변조 비율이 100 % 여야 함을 의미합니다.
예를 들어,이 값이 1 미만인 경우, 즉 변조 지수가 0.5이면 변조 된 출력은 다음 그림과 같습니다. 그것은Under-modulation. 이러한 파동을under-modulated wave.

변조 지수의 값이 1보다 크면, 즉 1.5 정도이면 파동은 over-modulated wave. 다음 그림과 같습니다.

변조 지수의 값이 증가함에 따라 반송파는 180 o 위상 반전을 경험하여 추가 측 파대를 유발하여 파동이 왜곡됩니다. 이러한과 변조 된 파동은 제거 할 수없는 간섭을 유발합니다.
AM 웨이브의 대역폭
Bandwidth(BW)는 신호의 최고 주파수와 최저 주파수 간의 차이입니다. 수학적으로 다음과 같이 쓸 수 있습니다.
$$ BW = f_ {최대}-f_ {분} $$
진폭 변조 파의 다음 방정식을 고려하십시오.
$$ s \ left (t \ right) = A_c \ left [1 + \ mu \ cos \ left (2 \ pi f_m t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$
$$ \ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) + A_c \ mu \ cos (2 \ pi f_ct) \ cos \ left (2 \ pi f_mt \ right) $$
$ \ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) + \ frac {A_c \ mu} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] + \ frac {A_c \ mu} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $
따라서 진폭 변조 파에는 세 가지 주파수가 있습니다. 그것들은 반송파 주파수 $ f_c $, 상부 측 파대 주파수 $ f_c + f_m $ 및 하부 측 파대 주파수 $ f_c-f_m $입니다.
여기,
$ f_ {max} = f_c + f_m $ 및 $ f_ {min} = f_c-f_m $
대역폭 공식에서 $ f_ {max} $ 및 $ f_ {min} $ 값을 대체합니다.
$$ BW = f_c + f_m- \ 왼쪽 (f_c-f_m \ 오른쪽) $$
$$ \ 오른쪽 화살표 BW = 2f_m $$
따라서 진폭 변조 파에 필요한 대역폭은 변조 신호 주파수의 두 배라고 할 수 있습니다.
AM 파동의 전력 계산
진폭 변조 파의 다음 방정식을 고려하십시오.
$ \ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) + \ frac {A_c \ mu} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ 오른쪽) t \ right] + \ frac {A_c \ mu} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $
AM 파의 전력은 반송파, 상부 측 파대 및 하부 측 파대 주파수 성분의 전력의 합과 같습니다.
$$ P_t = P_c + P_ {USB} + P_ {LSB} $$
cos 신호의 거듭 제곱에 대한 표준 공식은 다음과 같습니다.
$$ P = \ frac {{v_ {rms}} ^ {2}} {R} = \ frac {\ left (v_m / \ sqrt {2} \ right) ^ 2} {2} $$
어디,
$ v_ {rms} $는 cos 신호의 rms 값입니다.
$ v_m $는 cos 신호의 피크 값입니다.
먼저 반송파의 힘, 상부 측 파대와 하부 측 파대를 하나씩 찾아 보자.
캐리어 전력
$$ P_c = \ frac {\ left (A_c / \ sqrt {2} \ right) ^ 2} {R} = \ frac {{A_ {c}} ^ {2}} {2R} $$
상부 측 파대 전력
$$ P_ {USB} = \ frac {\ left (A_c \ mu / 2 \ sqrt {2} \ right) ^ 2} {R} = \ frac {{A_ {c}} ^ {2} {_ {\ mu}} ^ {2}} {8R} $$
마찬가지로 우리는 상부 측 파대 전력과 동일한 하부 측 파대 전력을 얻습니다.
$$ P_ {LSB} = \ frac {{A_ {c}} ^ {2} {_ {\ mu}} ^ {2}} {8R} $$
이제 AM 파의 힘을 얻기 위해이 세 가지 힘을 더해 봅시다.
$$ P_t = \ frac {{A_ {c}} ^ {2}} {2R} + \ frac {{A_ {c}} ^ {2} {_ {\ mu}} ^ {2}} {8R} + \ frac {{A_ {c}} ^ {2} {_ {\ mu}} ^ {2}} {8R} $$
$$ \ Rightarrow P_t = \ left (\ frac {{A_ {c}} ^ {2}} {2R} \ right) \ left (1+ \ frac {\ mu ^ 2} {4} + \ frac {\ mu ^ 2} {4} \ right) $$
$$ \ Rightarrow P_t = P_c \ left (1+ \ frac {\ mu ^ 2} {2} \ right) $$
반송파 전력과 변조 지수를 알고있을 때 위의 공식을 사용하여 AM 파의 전력을 계산할 수 있습니다.
변조 지수 $ \ mu = 1 $이면 AM 파의 전력은 반송파 전력의 1.5 배입니다. 따라서 AM 파를 전송하는 데 필요한 전력은 완벽한 변조를 위해 반송파 전력의 1.5 배입니다.
이전 장에서 진폭 변조에 사용 된 매개 변수에 대해 설명했습니다. 각 매개 변수에는 고유 한 공식이 있습니다. 이러한 공식을 사용하여 각각의 매개 변수 값을 찾을 수 있습니다. 이 장에서는 진폭 변조의 개념을 기반으로 몇 가지 문제를 해결해 보겠습니다.
문제 1
변조 신호 $ m \ left (t \ right) = 10 \ cos \ left (2 \ pi \ times 10 ^ 3 t \ right) $는 반송파 신호 $ c \ left (t \ right) = 50으로 진폭 변조됩니다. \ cos \ left (2 \ pi \ times 10 ^ 5 t \ right) $. AM 파를 전송하는 데 필요한 변조 지수, 반송파 전력 및 전력을 찾습니다.
해결책
주어진 신호를 변조하는 방정식은 다음과 같습니다.
$$ m \ left (t \ right) = 10 \ cos \ left (2 \ pi \ times 10 ^ 3 t \ right) $$
우리는 신호 변조의 표준 방정식을 다음과 같이 알고 있습니다.
$$ m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right) $$
위의 두 방정식을 비교하면
변조 신호의 진폭 ($ A_m = 10V $)
변조 신호의 주파수는 $$ f_m = 10 ^ 3 Hz = 1 KHz $$입니다.
주어진 캐리어 신호의 방정식은 다음과 같습니다.
$$ c \ left (t \ right) = 50 \ cos \ left (2 \ pi \ times 10 ^ 5t \ right) $$
반송파 신호의 표준 방정식은 다음과 같습니다.
$$ c \ 왼쪽 (t \ 오른쪽) = A_c \ cos \ 왼쪽 (2 \ pi f_ct \ 오른쪽) $$
이 두 방정식을 비교하면
반송파 신호의 진폭 ($ A_c = 50volts $)
$ f_c = 10 ^ 5 Hz = 100 KHz $로 반송파 신호의 주파수
우리는 변조 지수의 공식을 다음과 같이 알고 있습니다.
$$ \ mu = \ frac {A_m} {A_c} $$
위 공식에서 $ A_m $ 및 $ A_c $ 값을 대체하십시오.
$$ \ mu = \ frac {10} {50} = 0.2 $$
따라서 modulation index is 0.2 변조 비율은 20 %입니다.
Carrier power, $ P_c = $의 공식은 다음과 같습니다.
$$ P_c = \ frac {{A_ {c}} ^ {2}} {2R} $$
$ R = 1 \ Omega $를 가정하고 위 공식에서 $ A_c $ 값을 대체합니다.
$$ P_c = \ frac {\ left (50 \ right) ^ 2} {2 \ left (1 \ right)} = 1250W $$
따라서 Carrier power, $ P_c $는 1250 watts.
우리는 공식을 알고 있습니다 power 에 필요 transmitting AM 파도는
$$ \ Rightarrow P_t = P_c \ left (1+ \ frac {\ mu ^ 2} {2} \ right) $$
위 공식에서 $ P_c $ 및 $ \ mu $ 값을 대체하십시오.
$$ P_t = 1250 \ 왼쪽 (1+ \ frac {\ 왼쪽 (0.2 \ 오른쪽) ^ 2} {2} \ 오른쪽) = 1275W $$
따라서 power required for transmitting AM 파도는 1275 watts.
문제 2
진 폭파의 방정식은 $ s \ left (t \ right) = 20 \ left [1 + 0.8 \ cos \ left (2 \ pi \ times 10 ^ 3t \ right) \ right] \ cos \ left (4 \ pi \ times 10 ^ 5t \ right) $. 반송파 전력, 총 측 파대 전력 및 AM 파의 대역폭을 찾으십시오.
해결책
주어진 경우 진폭 변조 파의 방정식은 다음과 같습니다.
$$ s \ left (t \ right) = 20 \ left [1 + 0.8 \ cos \ left (2 \ pi \ times 10 ^ 3t \ right) \ right] \ cos \ left (4 \ pi \ times 10 ^ 5t \ 오른쪽) $$
위의 방정식을 다음과 같이 다시 작성하십시오.
$$ s \ left (t \ right) = 20 \ left [1 + 0.8 \ cos \ left (2 \ pi \ times 10 ^ 3t \ right) \ right] \ cos \ left (2 \ pi \ times 2 \ times 10 ^ 5t \ 오른쪽) $$
진폭 변조 파의 방정식은
$$ s \ left (t \ right) = A_c \ left [1+ \ mu \ cos \ left (2 \ pi f_mt \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$
위의 두 방정식을 비교하면
반송파 신호의 진폭 ($ A_c = 20V $)
$ \ mu = 0.8 $로 변조 지수
변조 신호의 주파수 ($ f_m = 10 ^ 3Hz = 1KHz $)
반송파 신호의 주파수 ($ f_c = 2 \ times 10 ^ 5Hz = 200KHz $)
Carrier power의 공식, $ P_c $ is
$$ P_c = \ frac {{A_ {e}} ^ {2}} {2R} $$
$ R = 1 \ Omega $를 가정하고 위 공식에서 $ A_c $ 값을 대체합니다.
$$ P_c = \ frac {\ left (20 \ right) ^ 2} {2 \ left (1 \ right)} = 200W $$
따라서 Carrier power, $ P_c $는 200watts.
총 측 파대 전력의 공식은
$$ P_ {SB} = \ frac {P_c \ mu ^ 2} {2} $$
위 공식에서 $ P_c $ 및 $ \ mu $ 값을 대체하십시오.
$$ P_ {SB} = \ frac {200 \ times \ left (0.8 \ right) ^ 2} {2} = 64W $$
따라서 total side band power 이다 64 watts.
AM 파의 대역폭 공식은
$$ BW = 2f_m $$
위 공식에서 $ f_m $ 값을 대체하십시오.
$$ BW = 2 \ 왼쪽 (1K \ 오른쪽) = 2 KHz $$
따라서 bandwidth AM 파의 2 KHz.
이 장에서는 진폭 변조 파를 생성하는 변조기에 대해 설명하겠습니다. 다음 두 변조기는 AM 파를 생성합니다.
- 제곱 법칙 변조기
- 스위칭 변조기
제곱 법칙 변조기
다음은 제곱 법칙 변조기의 블록 다이어그램입니다.

변조 및 반송파 신호를 각각 $ m \ left (t \ right) $ 및 $ A \ cos \ left (2 \ pi f_ct \ right) $로 표시합니다. 이 두 신호는 여름 (가산기) 블록에 대한 입력으로 적용됩니다. 이 여름 블록은 변조 및 반송파 신호를 더한 출력을 생성합니다. 수학적으로 다음과 같이 쓸 수 있습니다.
$$ V_1t = m \ 왼쪽 (t \ 오른쪽) + A_c \ cos \ 왼쪽 (2 \ pi f_ct \ 오른쪽) $$
이 신호 $ V_1t $는 다이오드와 같은 비선형 장치에 대한 입력으로 적용됩니다. 다이오드의 특성은 제곱 법칙과 밀접한 관련이 있습니다.
$ V_2t = k_1V_1 \ left (t \ right) + k_2V_1 ^ 2 \ left (t \ right) $ (방정식 1)
여기서 $ k_1 $ 및 $ k_2 $는 상수입니다.
방정식 1에서 $ V_1 \ left (t \ right) $를 대체하십시오.
$$ V_2 \ left (t \ right) = k_1 \ left [m \ left (t \ right) + A_c \ cos \ left (2 \ pi f_ct \ right) \ right] + k_2 \ left [m \ left (t \ right) + A_c \ cos \ left (2 \ pi f_ct \ right) \ right] ^ 2 $$
$ \ Rightarrow V_2 \ left (t \ right) = k_1 m \ left (t \ right) + k_1 A_c \ cos \ left (2 \ pi f_ct \ right) + k_2 m ^ 2 \ left (t \ right) + $
$ k_2A_c ^ 2 \ cos ^ 2 \ left (2 \ pi f_ct \ right) + 2k_2m \ left (t \ right) A_c \ cos \ left (2 \ pi f_ct \ right) $
$ \ Rightarrow V_2 \ left (t \ right) = k_1 m \ left (t \ right) + k_2 m ^ 2 \ left (t \ right) + k_2 A ^ 2_c \ cos ^ 2 \ left (2 \ pi f_ct \ 오른쪽) + $
$ k_1A_c \ left [1+ \ left (\ frac {2k_2} {k_1} \ right) m \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $
위 방정식의 마지막 항은 원하는 AM 파를 나타내며 위 방정식의 처음 세 항은 원하지 않습니다. 따라서 대역 통과 필터를 사용하면 AM 웨이브 만 통과시키고 처음 세 항을 제거 할 수 있습니다.
따라서 제곱 법칙 변조기의 출력은 다음과 같습니다.
$$ s \ left (t \ right) = k_1A_c \ left [1+ \ left (\ frac {2k_2} {k_1} \ right) m \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ 오른쪽) $$
AM 파의 표준 방정식은
$$ s \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$
여기서 $ K_a $는 진폭 감도입니다.
제곱 법칙 변조기의 출력을 AM 파의 표준 방정식과 비교하여 스케일링 계수를 $ k_1 $로, 진폭 감도 $ k_a $를 $ \ frac {2k_2} {k1} $로 얻습니다.
스위칭 변조기
다음은 스위칭 변조기의 블록 다이어그램입니다.

스위칭 변조기는 제곱 법칙 변조기와 유사합니다. 유일한 차이점은 제곱 법칙 변조기에서는 다이오드가 비선형 모드로 작동하는 반면, 스위칭 변조기에서는 다이오드가 이상적인 스위치로 작동해야한다는 것입니다.
변조 및 반송파 신호를 각각 $ m \ left (t \ right) $ 및 $ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $로 표시합니다. 이 두 신호는 여름 (가산기) 블록에 대한 입력으로 적용됩니다. Summer 블록은 변조 및 반송 신호를 추가 한 출력을 생성합니다. 수학적으로 다음과 같이 쓸 수 있습니다.
$$ V_1 \ left (t \ right) = m \ left (t \ right) + c \ left (t \ right) = m \ left (t \ right) + A_c \ cos \ left (2 \ pi f_ct \ right ) $$
이 신호 $ V_1 \ left (t \ right) $는 다이오드의 입력으로 적용됩니다. 변조 신호의 크기는 반송파 신호 $ A_c $의 진폭과 비교할 때 매우 작다고 가정합니다. 따라서 다이오드의 ON 및 OFF 동작은 캐리어 신호 $ c \ left (t \ right) $에 의해 제어됩니다. 즉, 다이오드는 $ c \ left (t \ right)> 0 $ 일 때 순방향 바이어스되고 $ c \ left (t \ right) <0 $ 일 때 역방향 바이어스됩니다.
따라서 다이오드의 출력은
$$ V_2 \ left (t \ right) = \ left \ {\ begin {matrix} V_1 \ left (t \ right) & if & c \ left (t \ right)> 0 \\ 0 & if & c \ left (t \ right) <0 \ end {matrix} \ right. $$
우리는 이것을 다음과 같이 추정 할 수 있습니다.
$ V_2 \ left (t \ right) = V_1 \ left (t \ right) x \ left (t \ right) $ (수식 2)
여기서 $ x \ left (t \ right) $는 기간이 $ T = \ frac {1} {f_c} $ 인 주기적 펄스 트레인입니다.

이 주기적 펄스열의 푸리에 급수 표현은 다음과 같습니다.
$$ x \ left (t \ right) = \ frac {1} {2} + \ frac {2} {\ pi} \ sum_ {n = 1} ^ {\ infty} \ frac {\ left (-1 \ 오른쪽) ^ n-1} {2n-1} \ cos \ left (2 \ pi \ left (2n-1 \ right) f_ct \ right) $$
$$ \ Rightarrow x \ left (t \ right) = \ frac {1} {2} + \ frac {2} {\ pi} \ cos \ left (2 \ pi f_ct \ right)-\ frac {2} { 3 \ pi} \ cos \ left (6 \ pi f_ct \ right) + .... $$
방정식 2에서 $ V_1 \ left (t \ right) $ 및 $ x \ left (t \ right) $ 값을 대체하십시오.
$ V_2 \ left (t \ right) = \ left [m \ left (t \ right) + A_c \ cos \ left (2 \ pi f_ct \ right) \ right] \ left [\ frac {1} {2} + \ frac {2} {\ pi} \ cos \ left (2 \ pi f_ct \ right)-\ frac {2} {3 \ pi} \ cos \ left (6 \ pi f_ct \ right) + ..... \ 오른쪽] $
$ V_2 \ left (t \ right) = \ frac {m \ left (t \ right)} {2} + \ frac {A_c} {2} \ cos \ left (2 \ pi f_ct \ right) + \ frac { 2m \ left (t \ right)} {\ pi} \ cos \ left (2 \ pi f_ct \ right) + \ frac {2A_c} {\ pi} \ cos ^ 2 \ left (2 \ pi f_ct \ right)- $
$ \ frac {2m \ left (t \ right)} {3 \ pi} \ cos \ left (6 \ pi f_ct \ right)-\ frac {2A_c} {3 \ pi} \ cos \ left (2 \ pi f_ct \ right) \ cos \ left (6 \ pi f_ct \ right) + ..... $
$ V_2 \ left (t \ right) = \ frac {A_c} {2} \ left (1+ \ left (\ frac {4} {\ pi A_c} \ right) m \ left (t \ right) \ right) \ cos \ left (2 \ pi f_ct \ right) + \ frac {m \ left (t \ right)} {2} + \ frac {2A_c} {\ pi} \ cos ^ 2 \ left (2 \ pi f_ct \ 오른쪽)-$
$ \ frac {2m \ left (t \ right)} {3 \ pi} \ cos \ left (6 \ pi f_ct \ right)-\ frac {2A_c} {3 \ pi} \ cos \ left (2 \ pi f_ct \ right) \ cos \ left (6 \ pi f_ct \ right) + ..... $
1 개 번째 상기 식의 용어는 원하는 AM 파형을 나타내고, 나머지 조건은 원하지 않는 조건이다. 따라서 대역 통과 필터를 사용하면 AM 파만 통과시키고 나머지 항을 제거 할 수 있습니다.
따라서 스위칭 변조기의 출력은
$$ s \ left (t \ right) = \ frac {A_c} {2} \ left (1+ \ left (\ frac {4} {\ pi A_c} \ right) m \ left (t \ right) \ right ) \ cos \ left (2 \ pi f_ct \ right) $$
우리는 AM 파의 표준 방정식이
$$ s \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$
여기서 $ k_a $는 진폭 감도입니다.
스위칭 변조기의 출력을 AM 파의 표준 방정식과 비교하여 스케일링 계수를 0.5로, 진폭 감도 $ k_a $를 $ \ frac {4} {\ pi A_c} $로 얻습니다.
변조 파에서 원본 메시지 신호를 추출하는 과정은 다음과 같습니다. detection 또는 demodulation. 변조 된 파를 복조하는 회로는demodulator. 다음 복조기 (검출기)는 AM 파를 복조하는 데 사용됩니다.
- 제곱 법칙 복조기
- 봉투 감지기
제곱 법칙 복조기
Square law 복조기는 저수준 AM 파를 복조하는 데 사용됩니다. 다음은 블록 다이어그램입니다.square law demodulator.

이 복조기는 제곱 법칙 장치와 저역 통과 필터를 포함합니다. AM 웨이브 $ V_1 \ left (t \ right) $는이 복조기에 입력으로 적용됩니다.
AM 파의 표준 형태는
$$ V_1 \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$
제곱 법칙 장치의 입력과 출력 사이의 수학적 관계는 다음과 같습니다.
$ V_2 \ left (t \ right) = k_1V_1 \ left (t \ right) + k_2V_1 ^ 2 \ left (t \ right) $ (수식 1)
어디,
$ V_1 \ left (t \ right) $는 제곱 법칙 장치의 입력으로, AM 파동 일뿐입니다.
$ V_2 \ left (t \ right) $는 제곱 법칙 장치의 출력입니다.
$ k_1 $ 및 $ k_2 $는 상수입니다.
방정식 1에서 $ V_1 \ left (t \ right) $를 대체합니다.
$$ V_2 \ left (t \ right) = k_1 \ left (A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) \ right) + k_2 \ 왼쪽 (A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) \ right) ^ 2 $$
$ \ Rightarrow V_2 \ left (t \ right) = k_1A_c \ cos \ left (2 \ pi f_ct \ right) + k_1A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) + $
$ k_2 {A_ {c}} ^ {2} \ left [1+ {K_ {a}} ^ {2} m ^ 2 \ left (t \ right) + 2k_am \ left (t \ right) \ right] \ 왼쪽 (\ frac {1+ \ cos \ left (4 \ pi f_ct \ right)} {2} \ right) $
$ \ Rightarrow V_2 \ left (t \ right) = k_1A_c \ cos \ left (2 \ pi f_ct \ right) + k_1A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) + \ frac { K_2 {A_ {c}} ^ {2}} {2} + $
$ \ frac {K_2 {A_ {c}} ^ {2}} {2} \ cos \ left (4 \ pi f_ct \ right) + \ frac {k_2 {A_ {c}} ^ {2} {k_ {a }} ^ {2} m ^ 2 \ left (t \ right)} {2} + \ frac {k_2 {A_ {c}} ^ {2} {k_ {a}} ^ {2} m ^ 2 \ left (t \ 오른쪽)} {2} \ cos \ left (4 \ pi f_ct \ right) + $
$ k_2 {A_ {c}} ^ {2} k_am \ left (t \ right) + k_2 {A_ {c}} ^ {2} k_am \ left (t \ right) \ cos \ left (4 \ pi f_ct \ 오른쪽) $
위 방정식에서 $ k_2 {A_ {c}} ^ {2} k_am \ left (t \ right) $라는 용어는 메시지 신호의 스케일링 된 버전입니다. 저역 통과 필터를 통해 위의 신호를 전달하여 추출 할 수 있으며 DC 구성 요소 $ \ frac {k_2 {A_ {c}} ^ {2}} {2} $는 커플 링 커패시터를 사용하여 제거 할 수 있습니다.
봉투 감지기
엔벨로프 감지기는 높은 수준의 AM 파를 감지 (복조)하는 데 사용됩니다. 다음은 엔벨로프 검출기의 블록 다이어그램입니다.

이 엔벨로프 감지기는 다이오드와 저역 통과 필터로 구성됩니다. 여기서 다이오드는 주요 감지 요소입니다. 따라서 엔벨로프 감지기는diode detector. 저역 통과 필터는 저항과 커패시터의 병렬 조합을 포함합니다.
AM 파 $ s \ left (t \ right) $는이 검출기에 대한 입력으로 적용됩니다.
우리는 AM 파의 표준 형태가
$$ s \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$
AM 파의 양의 반주기에서 다이오드는 전도되고 커패시터는 AM 파의 피크 값까지 충전됩니다. AM 파의 값이이 값보다 작 으면 다이오드가 역 바이어스됩니다. 따라서 커패시터는 저항을 통해 방전됩니다.RAM 파의 다음 양의 반주기까지. AM 파의 값이 커패시터 전압보다 크면 다이오드가 전도되고 프로세스가 반복됩니다.
커패시터가 매우 빠르게 충전되고 매우 느리게 방전되는 방식으로 구성 요소 값을 선택해야합니다. 결과적으로 변조 신호와 거의 유사한 AM 파의 포락선과 동일한 커패시터 전압 파형을 얻을 수 있습니다.
진폭 변조 과정에서 변조 된 파는 반송파와 두 개의 측 파대로 구성됩니다. 변조 된 파는 측 파대에만 정보가 있습니다.Sideband 이는 반송파 주파수의 더 낮은 주파수와 더 높은 주파수 인 전력을 포함하는 주파수 대역 일뿐입니다.
두 개의 측 파대와 함께 반송파를 포함하는 신호의 전송은 다음과 같이 불릴 수 있습니다. Double Sideband Full Carrier 시스템 또는 단순히 DSBFC. 다음 그림과 같이 플롯됩니다.

그러나 이러한 전송은 비효율적입니다. 전력의 2/3가 정보를 전달하지 않는 캐리어에서 낭비되고 있기 때문입니다.
이 반송파가 억제되고 절약 된 전력이 두 측 파대에 분배되면 이러한 프로세스를 다음과 같이 호출합니다. Double Sideband Suppressed Carrier 시스템 또는 단순히 DSBSC. 다음 그림과 같이 플롯됩니다.

수학적 표현
이전 장에서 고려했던 변조 및 반송파 신호에 대한 동일한 수학적 표현을 고려해 보겠습니다.
즉, 변조 신호
$$ m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right) $$
반송파 신호
$$ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $$
수학적으로 우리는 equation of DSBSC wave 변조 및 반송 신호의 곱으로.
$$ s \ 왼쪽 (t \ 오른쪽) = m \ 왼쪽 (t \ 오른쪽) c \ 왼쪽 (t \ 오른쪽) $$
$$ \ Rightarrow s \ left (t \ right) = A_mA_c \ cos \ left (2 \ pi f_mt \ right) \ cos \ left (2 \ pi f_ct \ right) $$
DSBSC 웨이브의 대역폭
대역폭 (BW)의 공식은
$$ BW = f_ {최대} -f_ {분} $$
DSBSC 변조 파의 방정식을 고려하십시오.
$$ s \ left (t \ right) = A_mA_c \ cos \ left (2 \ pi f_mt \ right) \ cos (2 \ pi f_ct) $$
$$ \ 오른쪽 화살표 s \ 왼쪽 (t \ 오른쪽) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] + \ frac {A_mA_c} {2 } \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $$
DSBSC 변조 파에는 2 개의 주파수 만 있습니다. 따라서 최대 및 최소 주파수는 각각 $ f_c + f_m $ 및 $ f_c-f_m $입니다.
즉,
$ f_ {max} = f_c + f_m $ 및 $ f_ {min} = f_c-f_m $
대역폭 공식에서 $ f_ {max} $ 및 $ f_ {min} $ 값을 대체합니다.
$$ BW = f_c + f_m- \ 왼쪽 (f_c-f_m \ 오른쪽) $$
$$ \ 오른쪽 화살표 BW = 2f_m $$
따라서 DSBSC 파의 대역폭은 AM 파의 대역폭과 같으며 변조 신호 주파수의 두 배와 같습니다.
DSBSC Wave의 전력 계산
DSBSC 변조 파의 다음 방정식을 고려하십시오.
$$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] + \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $$
DSBSC 파의 전력은 상부 측 파대와 하부 측 파대 주파수 성분의 전력의 합과 같습니다.
$$ P_t = P_ {USB} + P_ {LSB} $$
cos 신호의 거듭 제곱에 대한 표준 공식은 다음과 같습니다.
$$ P = \ frac {{v_ {rms}} ^ {2}} {R} = \ frac {\ left (v_m \ sqrt {2} \ right) ^ 2} {R} $$
먼저 상부 측 파대와 하부 측 파대의 힘을 하나씩 찾아 보자.
상부 측 파대 전력
$$ P_ {USB} = \ frac {\ left (A_mA_c / 2 \ sqrt {2} \ right) ^ 2} {R} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8R} $$
마찬가지로 우리는 상부 측 파대 전력과 동일한 하부 측 파대 전력을 얻습니다.
$$ P_ {USB} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8R} $$
이제 DSBSC 파의 전력을 얻기 위해이 두 측 파대 전력을 추가하겠습니다.
$$ P_t = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8R} + \ frac {{A_ {m}} ^ {2} {A_ {c} } ^ {2}} {8R} $$
$$ \ Rightarrow P_t = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {4R} $$
따라서 DSBSC 파를 전송하는 데 필요한 전력은 두 측 파대의 전력과 같습니다.
이 장에서는 DSBSC 파를 생성하는 변조기에 대해 설명합니다. 다음 두 변조기는 DSBSC 파를 생성합니다.
- 균형 잡힌 변조기
- 링 변조기
균형 잡힌 변조기
다음은 Balanced 변조기의 블록 다이어그램입니다.

Balanced modulator두 개의 동일한 AM 변조기로 구성됩니다. 이 두 변조기는 반송파 신호를 억제하기 위해 균형 잡힌 구성으로 배열됩니다. 따라서 Balanced Modulator라고합니다.
동일한 캐리어 신호 $ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $가이 두 AM 변조기에 대한 입력 중 하나로 적용됩니다. 변조 신호 $ m \ left (t \ right) $는 상단 AM 변조기에 또 다른 입력으로 적용됩니다. 반면, 반대 극성을 가진 변조 신호 $ m \ left (t \ right) $, 즉 $ -m \ left (t \ right) $는 하부 AM 변조기에 또 다른 입력으로 적용됩니다.
상부 AM 변조기의 출력은
$$ s_1 \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$
낮은 AM 변조기의 출력은
$$ s_2 \ left (t \ right) = A_c \ left [1-k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$
$ s_1 \ left (t \ right) $에서 $ s_2 \ left (t \ right) $를 빼서 $ s \ left (t \ right) $ DSBSC 웨이브를 얻습니다. 여름 블록은이 작업을 수행하는 데 사용됩니다. 양수 부호가있는 $ s_1 \ left (t \ right) $ 및 음수 부호가있는 $ s_2 \ left (t \ right) $는 여름 블록에 대한 입력으로 적용됩니다. 따라서 summer 블록은 $ s_1 \ left (t \ right) $와 $ s_2 \ left (t \ right) $의 차이 인 $ s \ left (t \ right) $ 출력을 생성합니다.
$$ \ Rightarrow s \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) -A_c \ left [1-k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$
$$ \ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) + A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right)-A_c \ cos \ left (2 \ pi f_ct \ right) + $$
$ A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) $
$ \ Rightarrow s \ left (t \ right) = 2A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) $
우리는 DSBSC 파동의 표준 방정식이
$$ s \ left (t \ right) = A_cm \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) $$
여름 블록의 출력을 DSBSC 웨이브의 표준 방정식과 비교하여 스케일링 계수를 $ 2k_a $로 얻습니다.
링 변조기
다음은 링 변조기의 블록 다이어그램입니다.

이 다이어그램에서 4 개의 다이오드 $ D_1 $, $ D_2 $, $ D_3 $ 및 $ D_4 $는 링 구조로 연결됩니다. 따라서이 변조기는ring modulator. 이 다이어그램에는 두 개의 중앙 탭 변압기가 사용됩니다. 메시지 신호 $ m \ left (t \ right) $가 입력 트랜스포머에 적용됩니다. 반면에 캐리어 신호 $ c \ left (t \ right) $는 두 개의 중앙 탭 변압기 사이에 적용됩니다.
반송파 신호의 양의 반주기의 경우 다이오드 $ D_1 $ 및 $ D_3 $가 켜지고 다른 두 다이오드 $ D_2 $ 및 $ D_4 $가 꺼집니다. 이 경우 메시지 신호에 +1을 곱합니다.
반송파 신호의 음의 반주기의 경우 다이오드 $ D_2 $ 및 $ D_4 $가 켜지고 다른 두 다이오드 $ D_1 $ 및 $ D_3 $가 꺼집니다. 이 경우 메시지 신호에 -1을 곱합니다. 결과 DSBSC 웨이브에서 $ 180 ^ 0 $ 위상 편이가 발생합니다.
위의 분석에서 4 개의 다이오드 $ D_1 $, $ D_2 $, $ D_3 $ 및 $ D_4 $가 반송파 신호에 의해 제어된다고 말할 수 있습니다. 반송파가 구형파이면 $ c \ left (t \ right) $의 푸리에 급수 표현은 다음과 같이 표현됩니다.
$$ c \ left (t \ right) = \ frac {4} {\ pi} \ sum_ {n = 1} ^ {\ infty} \ frac {\ left (-1 \ right) ^ {n-1}} {2n-1} \ cos \ left [2 \ pi f_ct \ left (2n-1 \ right) \ right] $$
DSBSC wave $ s \ left (t \ right) $는 반송파 신호 $ c \ left (t \ right) $와 메시지 신호 $ m \ left (t \ right) $ ie의 곱입니다. ,
$$ s \ left (t \ right) = \ frac {4} {\ pi} \ sum_ {n = 1} ^ {\ infty} \ frac {\ left (-1 \ right) ^ {n-1}} {2n-1} \ cos \ left [2 \ pi f_ct \ left (2n-1 \ right) \ right] m \ left (t \ right) $$
위의 방정식은 링 변조기의 출력 변압기에서 얻은 DSBSC 파를 나타냅니다.
DSBSC 변조기는 product modulators 두 입력 신호의 곱인 출력을 생성합니다.
DSBSC 웨이브에서 원본 메시지 신호를 추출하는 과정을 DSBSC의 탐지 또는 복조라고합니다. 다음 복조기 (검출기)는 DSBSC 파를 복조하는 데 사용됩니다.
- 코히 런트 검출기
- 코스타스 루프
코히 런트 검출기
여기서, 동일한 반송파 신호 (DSBSC 신호 생성에 사용됨)가 메시지 신호를 감지하는 데 사용됩니다. 따라서이 탐지 과정을coherent 또는 synchronous detection. 다음은 코히 런트 검출기의 블록 다이어그램입니다.

이 과정에서 메시지 신호는 DSBSC 변조에 사용되는 반송파의 주파수와 위상이 동일한 반송파를 곱하여 DSBSC 파에서 추출 할 수 있습니다. 결과 신호는 저역 통과 필터를 통과합니다. 이 필터의 출력은 원하는 메시지 신호입니다.
DSBSC 웨이브를
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) m \ left (t \ right) $$
국부 발진기의 출력은 다음과 같습니다.
$$ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ phi \ right) $$
여기서 $ \ phi $는 DSBSC 변조에 사용되는 로컬 오실레이터 신호와 반송파 신호 간의 위상차입니다.
그림에서 제품 변조기의 출력을 다음과 같이 작성할 수 있습니다.
$$ v \ 왼쪽 (t \ 오른쪽) = s \ 왼쪽 (t \ 오른쪽) c \ 왼쪽 (t \ 오른쪽) $$
위 방정식에서 $ s \ left (t \ right) $ 및 $ c \ left (t \ right) $ 값을 대체하십시오.
$$ \ Rightarrow v \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) m \ left (t \ right) A_c \ cos \ left (2 \ pi f_ct + \ phi \ right) $$
$ = {A_ {c}} ^ {2} \ cos \ left (2 \ pi f_ct \ right) \ cos \ left (2 \ pi f_ct + \ phi \ right) m \ left (t \ right) $
$ = \ frac {{A_ {c}} ^ {2}} {2} \ left [\ cos \ left (4 \ pi f_ct + \ phi \ right) + \ cos \ phi \ right] m \ left (t \ 오른쪽) $
$$ v \ left (t \ right) = \ frac {{A_ {c}} ^ {2}} {2} \ cos \ phi m \ left (t \ right) + \ frac {{A_ {c}} ^ {2}} {2} \ cos \ left (4 \ pi f_ct + \ phi \ right) m \ left (t \ right) $$
위의 방정식에서 첫 번째 항은 메시지 신호의 스케일 된 버전입니다. 위의 신호를 저역 통과 필터를 통해 전달하여 추출 할 수 있습니다.
따라서 저역 통과 필터의 출력은
$$ v_0t = \ frac {{A_ {c}} ^ {2}} {2} \ cos \ phi m \ left (t \ right) $$
복조 된 신호 진폭은 $ \ phi = 0 ^ 0 $ 일 때 최대가됩니다. 이것이 국부 발진기 신호와 반송파 신호가 위상이 같아야하는 이유입니다. 즉,이 두 신호간에 위상차가 없어야합니다.
$ \ phi = \ pm 90 ^ 0 $ 일 때 복조 된 신호 진폭은 0이됩니다. 이 효과는quadrature null effect.
코스타스 루프
Costas 루프는 반송파 신호 (DSBSC 변조에 사용됨)와 국부적으로 생성 된 신호를 위상으로 만드는 데 사용됩니다. 다음은 Costas 루프의 블록 다이어그램입니다.

Costas loop공통 입력 $ s \ left (t \ right) $, 즉 DSBSC 웨이브가있는 두 개의 제품 변조기로 구성됩니다. 두 제품 변조기에 대한 다른 입력은Voltage Controlled Oscillator (VCO)는 그림과 같이 제품 변조기 중 하나로 $ -90 ^ 0 $ 위상 편이를 사용합니다.
우리는 DSBSC 파동의 방정식이
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) m \ left (t \ right) $$
VCO의 출력을
$$ c_1 \ left (t \ right) = \ cos \ left (2 \ pi f_ct + \ phi \ right) $$
이 VCO 출력은 상위 곱 변조기의 캐리어 입력으로 적용됩니다.
따라서 상위 곱 변조기의 출력은
$$ v_1 \ 왼쪽 (t \ 오른쪽) = s \ 왼쪽 (t \ 오른쪽) c_1 \ 왼쪽 (t \ 오른쪽) $$
위 방정식에서 $ s \ left (t \ right) $ 및 $ c_1 \ left (t \ right) $ 값을 대체하십시오.
$$ \ Rightarrow v_1 \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) m \ left (t \ right) \ cos \ left (2 \ pi f_ct + \ phi \ right) $ $
단순화하면 $ v_1 \ left (t \ right) $가됩니다.
$$ v_1 \ left (t \ right) = \ frac {A_c} {2} \ cos \ phi m \ left (t \ right) + \ frac {A_c} {2} \ cos \ left (4 \ pi f_ct + \ phi \ 오른쪽) m \ 왼쪽 (t \ 오른쪽) $$
이 신호는 상위 저역 통과 필터의 입력으로 적용됩니다. 이 저역 통과 필터의 출력은 다음과 같습니다.
$$ v_ {01} \ left (t \ right) = \ frac {A_c} {2} \ cos \ phi m \ left (t \ right) $$
따라서이 저역 통과 필터의 출력은 변조 신호의 스케일 된 버전입니다.
$ -90 ^ 0 $ 위상 시프터의 출력은 다음과 같습니다.
$$ c_2 \ left (t \ right) = cos \ left (2 \ pi f_ct + \ phi-90 ^ 0 \ right) = \ sin \ left (2 \ pi f_ct + \ phi \ right) $$
이 신호는 하위 곱 변조기의 반송파 입력으로 적용됩니다.
하위 제품 변조기의 출력은 다음과 같습니다.
$$ v_2 \ 왼쪽 (t \ 오른쪽) = s \ 왼쪽 (t \ 오른쪽) c_2 \ 왼쪽 (t \ 오른쪽) $$
위 방정식에서 $ s \ left (t \ right) $ 및 $ c_2 \ left (t \ right) $ 값을 대체하십시오.
$$ \ Rightarrow v_2 \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) m \ left (t \ right) \ sin \ left (2 \ pi f_ct + \ phi \ right) $ $
단순화 후 $ v_2 \ left (t \ right) $
$$ v_2 \ left (t \ right) = \ frac {A_c} {2} \ sin \ phi m \ left (t \ right) + \ frac {A_c} {2} \ sin \ left (4 \ pi f_ct + \ 파이 \ 오른쪽) m \ 왼쪽 (t \ 오른쪽) $$
이 신호는 로우 패스 필터의 입력으로 적용됩니다. 이 저역 통과 필터의 출력은 다음과 같습니다.
$$ v_ {02} \ 왼쪽 (t \ 오른쪽) = \ frac {A_c} {2} \ sin \ phi m \ 왼쪽 (t \ 오른쪽) $$
이 저역 통과 필터의 출력은 상위 저역 통과 필터의 출력과 $ -90 ^ 0 $ 위상차가 있습니다.
이 두 개의 저역 통과 필터의 출력은 위상 판별 기의 입력으로 적용됩니다. 이 두 신호 간의 위상차에 따라 위상 판별 기는 DC 제어 신호를 생성합니다.
이 신호는 VCO 출력의 위상 오류를 수정하기 위해 VCO의 입력으로 적용됩니다. 따라서 반송파 신호 (DSBSC 변조에 사용됨)와 국부적으로 생성 된 신호 (VCO 출력)는 동 위상입니다.
이전 장에서 DSBSC 변조 및 복조에 대해 설명했습니다. DSBSC 변조 신호에는 두 개의 측 파대가 있습니다. 두 측 파대는 동일한 정보를 전달하므로 두 측 파대를 모두 전송할 필요가 없습니다. 하나의 측 파대를 제거 할 수 있습니다.
반송파와 함께 측 파대 중 하나를 억제하고 단일 측 파대를 전송하는 과정을 Single Sideband Suppressed Carrier 시스템 또는 단순히 SSBSC. 다음 그림과 같이 플롯됩니다.

위 그림에서는 반송파와 하부 측 파대가 억제되어 있습니다. 따라서 상부 측 파대가 전송에 사용됩니다. 마찬가지로 우리는 하부 측 파대를 전송하면서 반송파와 상부 측 파대를 억제 할 수 있습니다.
단일 측 파대를 전송하는이 SSBSC 시스템은 반송파와 다른 측 파대 모두에 할당 된 전력이이 단일 측 파대 전송에 활용되기 때문에 높은 전력을 가지고 있습니다.
수학적 표현
이전 장에서 고려했던 변조 및 반송파 신호에 대한 동일한 수학적 표현을 고려해 보겠습니다.
즉, 변조 신호
$$ m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right) $$
반송파 신호
$$ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $$
수학적으로 SSBSC 파동의 방정식을 다음과 같이 나타낼 수 있습니다.
$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] $ -상단 측 파대
또는
$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $ -하단 측 파대
SSBSC 웨이브의 대역폭
DSBSC 변조 파에는 두 개의 측 파대가 포함되어 있고 대역폭은 $ 2f_m $입니다. SSBSC 변조 파에는 측 파대가 하나만 포함되어 있으므로 대역폭은 DSBSC 변조 파 대역폭의 절반입니다.
즉, Bandwidth of SSBSC modulated wave = $ \ frac {2f_m} {2} = f_m $
따라서 SSBSC 변조 파의 대역폭은 $ f_m $이고 변조 신호의 주파수와 동일합니다.
SSBSC 웨이브의 전력 계산
SSBSC 변조 파의 다음 방정식을 고려하십시오.
$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] $ -상단 측 파대
또는
$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $ -하단 측 파대
SSBSC 파의 전력은 측 파대 주파수 구성 요소의 전력과 같습니다.
$$ P_t = P_ {USB} = P_ {LSB} $$
cos 신호의 거듭 제곱에 대한 표준 공식은 다음과 같습니다.
$$ P = \ frac {{v_ {rms}} ^ {2}} {R} = \ frac {\ left (v_m / \ sqrt {2} \ right) ^ 2} {R} $$
이 경우 상부 측 파대의 전력은 다음과 같습니다.
$$ P_ {USB} = \ frac {\ left (A_m A_c / 2 \ sqrt {2} \ right) ^ 2} {R} = \ frac {{A_ {m}} ^ {2} {A_ {c} } ^ {2}} {8R} $$
마찬가지로 우리는 상부 측 파대 전력과 동일한 하부 측 파대 전력을 얻습니다.
$$ P_ {LSB} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8R} $$
따라서 SSBSC 파의 힘은
$$ P_t = P_ {USB} = P_ {LSB} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8R} $$
장점
차지하는 대역폭 또는 스펙트럼 공간은 AM 및 DSBSC 파보다 적습니다.
더 많은 수의 신호를 전송할 수 있습니다.
전력이 절약됩니다.
고출력 신호를 전송할 수 있습니다.
소음이 적습니다.
신호 페이딩이 발생할 가능성이 적습니다.
단점
SSBSC 파의 생성 및 감지는 복잡한 프로세스입니다.
SSB 송신기와 수신기의 주파수 안정성이 우수하지 않으면 신호의 품질이 영향을받습니다.
응용
절전 요구 사항 및 낮은 대역폭 요구 사항에 적합합니다.
육상, 항공 및 해상 이동 통신에서.
지점 간 통신에서.
무선 통신에서.
텔레비전, 원격 측정 및 레이더 통신에서.
아마추어 라디오 등과 같은 군사 통신에서
이 장에서는 SSBSC 파를 생성하는 변조기에 대해 논의하겠습니다. 다음 두 가지 방법으로 SSBSC 웨이브를 생성 할 수 있습니다.
- 주파수 판별 방법
- 위상 차별 방법
주파수 식별 방법
다음 그림은 주파수 식별 방법을 사용하는 SSBSC 변조기의 블록 다이어그램을 보여줍니다.

이 방법에서는 먼저 제품 변조기를 사용하여 DSBSC 웨이브를 생성합니다. 그런 다음이 DSBSC 파를 대역 통과 필터의 입력으로 적용합니다. 이 대역 통과 필터는 SSBSC 웨이브 인 출력을 생성합니다.
원하는 SSBSC 파형의 스펙트럼으로 대역 통과 필터의 주파수 범위를 선택합니다. 즉, 대역 통과 필터는 상부 측 파대 또는 하부 측 파대를 갖는 각 SSBSC 파를 얻기 위해 상부 측 파대 또는 하부 측 파대 주파수로 튜닝 될 수 있습니다.
위상 차별 방법
다음 그림은 위상 식별 방법을 사용하는 SSBSC 변조기의 블록 다이어그램을 보여줍니다.

이 블록 다이어그램은 2 개의 제품 변조기, 2 개의 $ -90 ^ 0 $ 위상 시프터, 1 개의 로컬 오실레이터 및 1 개의 여름 블록으로 구성됩니다. 곱 변조기는 두 입력의 곱인 출력을 생성합니다. $ -90 ^ 0 $ 위상 시프터는 입력에 대해 $ -90 ^ 0 $의 위상 지연을 갖는 출력을 생성합니다.
국부 발진기는 반송파 신호를 생성하는 데 사용됩니다. Summer 블록은 두 입력의 합 또는 입력의 극성에 따른 두 입력의 차이 인 출력을 생성합니다.
변조 신호 $ A_m \ cos \ left (2 \ pi f_mt \ right) $ 및 반송파 신호 $ A_c \ cos \ left (2 \ pi f_ct \ right) $는 상위 곱 변조기에 대한 입력으로 직접 적용됩니다. 따라서 상위 곱 변조기는이 두 입력의 곱인 출력을 생성합니다.
상위 제품 변조기의 출력은 다음과 같습니다.
$$ s_1 \ left (t \ right) = A_mA_c \ cos \ left (2 \ pi f_mt \ right) \ cos \ left (2 \ pi f_ct \ right) $$
$$ \ Rightarrow s_1 \ left (t \ right) = \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] + \ cos \ 왼쪽 [2 \ pi \ left (f_c-f_m \ right) t \ right] \ right \} $$
변조 신호 $ A_m \ cos \ left (2 \ pi f_mt \ right) $ 및 반송파 신호 $ A_c \ cos \ left (2 \ pi f_ct \ right) $는 다음과 같이 적용하기 전에 $ -90 ^ 0 $만큼 위상 편이됩니다. 낮은 제품 변조기에 대한 입력. 따라서 더 낮은 곱 변조기는이 두 입력의 곱인 출력을 생성합니다.
낮은 제품 변조기의 출력은 다음과 같습니다.
$$ s_2 \ left (t \ right) = A_mA_c \ cos \ left (2 \ pi f_mt-90 ^ 0 \ right) \ cos \ left (2 \ pi f_ct-90 ^ 0 \ right) $$
$ \ Rightarrow s_2 \ left (t \ right) = A_mA_c \ sin \ left (2 \ pi f_mt \ right) \ sin \ left (2 \ pi f_ct \ right) $
$ \ Rightarrow s_2 \ left (t \ right) = \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right]-\ cos \ left [2 \ pi \ 왼쪽 (f_c + f_m \ 오른쪽) t \ 오른쪽] \ 오른쪽 \} $
$ s_1 \ left (t \ right) $ 및 $ s_2 \ left (t \ right) $를 추가하여 더 낮은 측 파대를 갖는 SSBSC 변조 파 $ s \ left (t \ right) $를 얻으십시오.
$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] + \ cos \ left [2 \ pi \ 왼쪽 (f_c-f_m \ 오른쪽) t \ 오른쪽] \ 오른쪽 \} + $
$ \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right]-\ cos \ left [2 \ pi \ left (f_c + f_m \ 오른쪽) t \ 오른쪽] \ 오른쪽 \} $
$ \ Rightarrow s \ left (t \ right) = A_mA_c \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $
$ s_2 \ left (t \ right) $를 $ s_1 \ left (t \ right) $에서 빼면 SSBSC 변조 된 웨이브 $ s \ left (t \ right) $가 상위 측 파대를 갖습니다.
$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] + \ cos \ left [2 \ pi \ 왼쪽 (f_c-f_m \ 오른쪽) t \ 오른쪽] \ 오른쪽 \}-$
$ \ frac {A_mA_c} {2} \ left \ {\ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right]-\ cos \ left [2 \ pi \ left (f_c + f_m \ 오른쪽) t \ 오른쪽] \ 오른쪽 \} $
$ \ Rightarrow s \ left (t \ right) = A_mA_c \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] $
따라서 여름 블록에서 입력의 극성을 올바르게 선택하면 상위 측 파대 또는 하위 측 파대를 갖는 SSBSC 파를 얻을 수 있습니다.
SSBSC 파에서 원본 메시지 신호를 추출하는 과정을 SSBSC의 탐지 또는 복조라고합니다. 코히 런트 검출기는 SSBSC 파를 복조하는 데 사용됩니다.
코히 런트 검출기
여기서는 SSBSC 파를 생성하는 데 사용되는 동일한 반송파 신호가 메시지 신호를 감지하는 데 사용됩니다. 따라서이 탐지 과정을coherent 또는 synchronous detection. 다음은 코히 런트 검출기의 블록 다이어그램입니다.

이 과정에서 메시지 신호는 SSBSC 변조에 사용되는 반송파의 주파수와 위상이 동일한 반송파와 곱하여 SSBSC 파에서 추출 할 수 있습니다. 결과 신호는 저역 통과 필터를 통과합니다. 이 필터의 출력은 원하는 메시지 신호입니다.
다음을 고려하세요 SSBSC 파는 데 lower sideband.
$$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $$
국부 발진기의 출력은 다음과 같습니다.
$$ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $$
그림에서 제품 변조기의 출력을 다음과 같이 작성할 수 있습니다.
$$ v \ 왼쪽 (t \ 오른쪽) = s \ 왼쪽 (t \ 오른쪽) c \ 왼쪽 (t \ 오른쪽) $$
위 방정식에서 $ s \ left (t \ right) $ 및 $ c \ left (t \ right) $ 값을 대체하십시오.
$$ v \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] A_c \ cos \ left (2 \ pi f_ct \ 오른쪽) $$
$ = \ frac {A_m {A_ {c}} ^ {2}} {2} \ cos \ left [2 \ pi \ left (f_c -f_m \ right) t \ right] \ cos \ left (2 \ pi f_ct \ 오른쪽) $
$ = \ frac {A_m {A_ {c}} ^ {2}} {4} \ left \ {\ cos \ left [2 \ pi \ left (2f_c-fm \ right) \ right] + \ cos \ left ( 2 \ pi f_m \ 오른쪽) t \ 오른쪽 \} $
$ v \ left (t \ right) = \ frac {A_m {A_ {c}} ^ {2}} {4} \ cos \ left (2 \ pi f_mt \ right) + \ frac {A_m {A_ {c} } ^ {2}} {4} \ cos \ left [2 \ pi \ left (2f_c-f_m \ right) t \ right] $
위의 방정식에서 첫 번째 항은 메시지 신호의 스케일 된 버전입니다. 위의 신호를 저역 통과 필터를 통해 전달하여 추출 할 수 있습니다.
따라서 저역 통과 필터의 출력은
$$ v_0 \ left (t \ right) = \ frac {A_m {A_ {c}} ^ {2}} {4} \ cos \ left (2 \ pi f_mt \ right) $$
여기서 배율 인수는 $ \ frac {{A_ {c}} ^ {2}} {4} $입니다.
상부 측 파대를 갖는 SSBSC 파를 복조하기 위해 동일한 블록 다이어그램을 사용할 수 있습니다. 다음을 고려하세요SSBSC 파는 데 upper sideband.
$$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] $$
국부 발진기의 출력은 다음과 같습니다.
$$ c \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) $$
제품 변조기의 출력을 다음과 같이 작성할 수 있습니다.
$$ v \ 왼쪽 (t \ 오른쪽) = s \ 왼쪽 (t \ 오른쪽) c \ 왼쪽 (t \ 오른쪽) $$
위 방정식에서 $ s \ left (t \ right) $ 및 $ c \ left (t \ right) $ 값을 대체하십시오.
$$ \ 오른쪽 화살표 v \ 왼쪽 (t \ 오른쪽) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] A_c \ cos \ left (2 \ pi f_ct \ 오른쪽) $$
$ = \ frac {A_m {A_ {c}} ^ {2}} {2} \ cos \ left [2 \ pi \ left (f_c + f_m \ right) t \ right] \ cos \ left (2 \ pi f_ct \ 오른쪽) $
$ = \ frac {A_m {A_ {c}} ^ {2}} {4} \ left \ {\ cos \ left [2 \ pi \ left (2f_c + f_m \ right) t \ right] + \ cos \ left (2 \ pi f_mt \ right) \ right \} $
$ v \ left (t \ right) = \ frac {A_m {A_ {c}} ^ {2}} {4} \ cos \ left (2 \ pi f_mt \ right) + \ frac {A_m {A_ {c} } ^ {2}} {4} \ cos \ left [2 \ pi \ left (2f_c + f_m \ right) t \ right] $
위의 방정식에서 첫 번째 항은 메시지 신호의 스케일 된 버전입니다. 위의 신호를 저역 통과 필터를 통해 전달하여 추출 할 수 있습니다.
따라서 저역 통과 필터의 출력은 다음과 같습니다.
$$ v_0 \ left (t \ right) = \ frac {A_m {A_ {c}} ^ {2}} {4} \ cos \ left (2 \ pi f_mt \ right) $$
여기서도 스케일링 계수는 $ \ frac {{A_ {c}} ^ {2}} {4} $입니다.
따라서 코히 런트 검출기를 사용하여 두 경우 모두 동일한 복조 출력을 얻습니다.
이전 장에서 SSBSC 변조 및 복조에 대해 설명했습니다. SSBSC 변조 신호에는 측 파대 주파수가 하나만 있습니다. 이론적으로는 이상적인 대역 통과 필터를 사용하여 하나의 측 파대 주파수 성분을 완전히 얻을 수 있습니다. 그러나 실제로 우리는 전체 측 파대 주파수 성분을 얻지 못할 수 있습니다. 이로 인해 일부 정보가 손실됩니다.
이러한 손실을 방지하기 위해 DSBSC와 SSBSC 간의 절충안 인 기술이 선택됩니다. 이 기술은 다음과 같이 알려져 있습니다.Vestigial Side Band Suppressed Carrier (VSBSC)기술. "자취"라는 단어는 이름이 파생 된 "일부"를 의미합니다.
VSBSC Modulation흔적이라고 불리는 신호의 일부가 한 측 파대와 함께 변조되는 과정입니다. VSBSC 파의 주파수 스펙트럼은 다음 그림에 나와 있습니다.

상부 측 파대와 함께 하부 측 파대의 일부도이 기술에서 전송됩니다. 유사하게, 우리는 상부 측 파대의 일부와 함께 하부 측 파대를 전송할 수 있습니다. 간섭을 피하기 위해 매우 작은 폭의 보호 대역이 VSB의 양쪽에 배치됩니다. VSB 변조는 주로 텔레비전 전송에 사용됩니다.
VSBSC 변조의 대역폭
SSBSC 변조 파의 대역폭은 $ f_m $입니다. VSBSC 변조 파에는 다른 측 파대의 흔적과 함께 한 측 파대의 주파수 성분이 포함되어 있기 때문에 그 대역폭은 SSBSC 변조 파의 대역폭과 흔적 주파수 $ f_v $의 합이됩니다.
i.e., Bandwidth of VSBSC Modulated Wave = $f_m + f_v$
장점
다음은 VSBSC 변조의 장점입니다.
매우 효율적입니다.
AM 및 DSBSC 웨이브와 비교할 때 대역폭 감소.
높은 정확도가 필요하지 않기 때문에 필터 설계가 쉽습니다.
저주파 성분의 전송이 어려움없이 가능합니다.
좋은 위상 특성을 가지고 있습니다.
단점
다음은 VSBSC 변조의 단점입니다.
SSBSC 웨이브와 비교할 때 대역폭이 더 큽니다.
복조는 복잡합니다.
응용
VSBSC의 가장 눈에 띄는 표준 응용 프로그램은 TV 신호 전송입니다. 또한 이것은 대역폭 사용을 고려할 때 가장 편리하고 효율적인 기술입니다.
이제 VSBSC 파를 생성하는 변조기와 VSBSC 파를 하나씩 복조하는 복조기에 대해 살펴 보겠습니다.
VSBSC 생성
VSBSC 웨이브의 생성은 SSBSC 웨이브의 생성과 유사합니다. VSBSC 변조기는 다음 그림에 나와 있습니다.
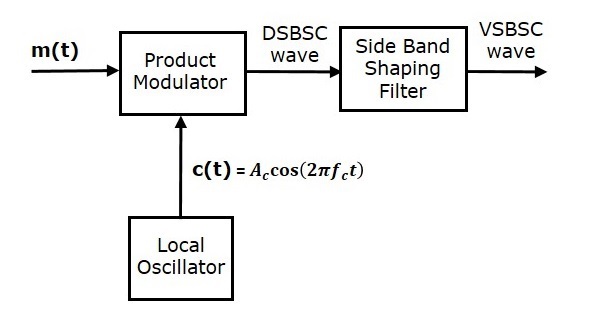
이 방법에서는 먼저 제품 변조기를 사용하여 DSBSC 웨이브를 생성합니다. 그런 다음이 DSBSC 파를 측 파대 형성 필터의 입력으로 적용합니다. 이 필터는 VSBSC 웨이브 인 출력을 생성합니다.
변조 신호 $ m \ left (t \ right) $ 및 반송파 신호 $ A_c \ cos \ left (2 \ pi f_ct \ right) $는 제품 변조기에 대한 입력으로 적용됩니다. 따라서 곱 변조기는이 두 입력의 곱인 출력을 생성합니다.
따라서 제품 변조기의 출력은 다음과 같습니다.
$$ p \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) m \ left (t \ right) $$
양쪽에 푸리에 변환 적용
$$ P \ left (f \ right) = \ frac {A_c} {2} \ left [M \ left (f-f_c \ right) + M \ left (f + f_c \ right) \ right] $$
위의 방정식은 DSBSC 주파수 스펙트럼의 방정식을 나타냅니다.
측 파대 형성 필터의 전달 함수를 $ H \ left (f \ right) $라고합니다. 이 필터에는 $ p \ left (t \ right) $ 입력이 있고 출력은 VSBSC 변조 파 $ s \ left (t \ right) $입니다. $ p \ left (t \ right) $ 및 $ s \ left (t \ right) $의 푸리에 변환은 각각 $ P \ left (t \ right) $ 및 $ S \ left (t \ right) $입니다.
수학적으로 $ S \ left (f \ right) $를 다음과 같이 쓸 수 있습니다.
$$ S \ 왼쪽 (t \ 오른쪽) = P \ 왼쪽 (f \ 오른쪽) H \ 왼쪽 (f \ 오른쪽) $$
위 방정식에서 $ P \ left (f \ right) $ 값을 대체하십시오.
$$ S \ left (f \ right) = \ frac {A_c} {2} \ left [M \ left (f-f_c \ right) + M \ left (f + f_c \ right) \ right] H \ left ( f \ 오른쪽) $$
위의 방정식은 VSBSC 주파수 스펙트럼의 방정식을 나타냅니다.
VSBSC의 복조
VSBSC 웨이브의 복조는 SSBSC 웨이브의 복조와 유사합니다. 여기서는 동일한 반송파 신호 (VSBSC 파 생성에 사용됨)가 메시지 신호를 감지하는 데 사용됩니다. 따라서이 탐지 과정을coherent 또는 synchronous detection. VSBSC 복조기는 다음 그림에 나와 있습니다.

이 과정에서 메시지 신호는 VSBSC 변조에 사용되는 반송파의 주파수와 위상이 동일한 반송파와 곱하여 VSBSC 파에서 추출 할 수 있습니다. 결과 신호는 저역 통과 필터를 통과합니다. 이 필터의 출력은 원하는 메시지 신호입니다.
VSBSC 파동을 $ s \ left (t \ right) $이고 반송파 신호를 $ A_c \ cos \ left (2 \ pi f_ct \ right) $라고합니다.
그림에서 제품 변조기의 출력을 다음과 같이 작성할 수 있습니다.
$$ v \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) s \ left (t \ right) $$
양쪽에 푸리에 변환 적용
$$ V \ left (f \ right) = \ frac {A_c} {2} \ left [S \ left (f-f_c \ right) + S \ left (f + f_c \ right) \ right] $$
우리가 알고 $ S \ (오른쪽 F를 \) 왼쪽 = \ FRAC {A_c가} {2} \ 왼쪽 [M \ 왼쪽 (F-f_c \ 오른쪽) + M \ 왼쪽 (F + f_c \ 오른쪽) \ 오른쪽] H \ 왼쪽 (f \ 오른쪽) $
위의 방정식에서 $ S \ left (f-f_c \ right) $와 $ S \ left (f + f_c \ right) $를 찾으세요.
$$ S \ left (f-f_c \ right) = \ frac {A_c} {2} \ left [M \ left (f-f_c-f_c \ right) + M \ left (f-f_c + f_c \ right) \ 오른쪽] H \ 왼쪽 (f-f_c \ 오른쪽) $$
$ \ 오른쪽 화살표 S \ 왼쪽 (f-f_c \ right) = \ frac {A_c} {2} \ left [M \ left (f-2f_c \ right) + M \ left (f \ right) \ right] H \ left (f-f_c \ 오른쪽) $
$$ S \ 왼쪽 (f + f_c \ 오른쪽) = \ frac {A_c} {2} \ 왼쪽 [M \ 왼쪽 (f + f_c-f_c \ 오른쪽) + M \ 왼쪽 (f + f_c + f_c \ 오른쪽) \ 오른쪽] H \ 왼쪽 (f + f_c \ 오른쪽) $$
$ \ 오른쪽 화살표 S \ 왼쪽 (f + f_c \ 오른쪽) = \ frac {A_c} {2} \ 왼쪽 [M \ 왼쪽 (f \ 오른쪽) + M \ 왼쪽 (f + 2f_c \ 오른쪽) \ 오른쪽] H \ 왼쪽 (f + f_c \ 오른쪽) $
$ V \ left (f \ right) $에서 $ S \ left (f-f_c \ right) $ 및 $ S \ left (f + f_c \ right) $ 값을 대체하십시오.
$ V (f) = \ frac {A_c} {2} [\ frac {A_c} {2} [M (f-2f_c) + M (f)] H (f-f_c) + $
$ \ frac {A_c} {2} [M (f) + M (f + 2f_c)] H (f + f_c)] $
$ \ Rightarrow V \ left (f \ right) = \ frac {{A_ {c}} ^ {2}} {4} M \ left (f \ right) \ left [H \ left (f-f_c \ right) + H \ 왼쪽 (f + f_c \ 오른쪽) \ 오른쪽] $
$ + \ frac {{A_ {c}} ^ {2}} {4} \ left [M \ left (f-2f_c \ right) H \ left (f-f_c \ right) + M \ left (f + 2f_c \ 오른쪽) H \ 왼쪽 (f + f_c \ 오른쪽) \ 오른쪽] $
위 방정식에서 첫 번째 항은 원하는 메시지 신호 주파수 스펙트럼의 스케일 된 버전을 나타냅니다. 위의 신호를 저역 통과 필터를 통해 전달하여 추출 할 수 있습니다.
$$ V_0 \ left (f \ right) = \ frac {{A_ {c}} ^ {2}} {4} M \ left (f \ right) \ left [H \ left (f-f_c \ right) + H \ 왼쪽 (f + f_c \ 오른쪽) \ 오른쪽] $$
연속파 변조에서 다른 유형의 변조는 Angle Modulation. 각도 변조는 반송파 신호의 주파수 또는 위상이 메시지 신호에 따라 달라지는 프로세스입니다.
각도 변조 파의 표준 방정식은 다음과 같습니다.
$$ s \ left (t \ right) = A_c \ cos \ theta _i \ left (t \ right) $$
어디,
$ A_c $는 변조 파의 진폭으로 반송파 신호의 진폭과 동일합니다.
$ \ theta _i \ left (t \ right) $는 변조 된 파동의 각도입니다.
각도 변조는 주파수 변조와 위상 변조로 더 나뉩니다.
Frequency Modulation 메시지 신호와 함께 반송파 신호의 주파수를 선형으로 변경하는 프로세스입니다.
Phase Modulation 메시지 신호와 함께 반송파 신호의 위상을 선형으로 변경하는 프로세스입니다.
이제 이에 대해 자세히 논의하겠습니다.
주파수 변조
진폭 변조에서 반송파 신호의 진폭은 다양합니다. 반면에Frequency Modulation (FM), 반송파 신호의 주파수는 변조 신호의 순간 진폭에 따라 달라집니다.
따라서 주파수 변조에서 반송파 신호의 진폭과 위상은 일정하게 유지됩니다. 이것은 다음 그림을 보면 더 잘 이해할 수 있습니다.
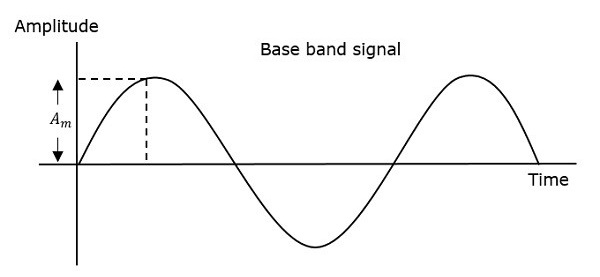


변조 또는 메시지 신호의 진폭이 증가하면 변조 파의 주파수가 증가합니다. 마찬가지로 변조 신호의 진폭이 감소하면 변조 파의 주파수가 감소합니다. 변조 신호의 진폭이 0 일 때 변조 파의 주파수는 일정하게 유지되고 반송파 신호의 주파수와 동일합니다.
수학적 표현
FM 변조에서 순간 주파수 $ f_i $에 대한 방정식은 다음과 같습니다.
$$ f_i = f_c + k_fm \ 왼쪽 (t \ 오른쪽) $$
어디,
$ f_c $는 반송파 주파수입니다.
$ k_t $는 주파수 민감도입니다.
$ m \ left (t \ right) $는 메시지 신호입니다.
각 주파수 $ \ omega_i $와 각도 $ \ theta _i \ left (t \ right) $ 사이의 관계를 다음과 같이 알고 있습니다.
$$ \ omega_i = \ frac {d \ theta _i \ left (t \ right)} {dt} $$
$ \ Rightarrow 2 \ pi f_i = \ frac {d \ theta _i \ left (t \ right)} {dt} $
$ \ Rightarrow \ theta _i \ left (t \ right) = 2 \ pi \ int f_i dt $
위 방정식에서 $ f_i $ 값을 대입합니다.
$$ \ theta _i \ left (t \ right) = 2 \ pi \ int \ left (f_c + k_f m \ left (t \ right) \ right) dt $$
$ \ Rightarrow \ theta _i \ left (t \ right) = 2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt $
각도 변조 파의 표준 방정식에서 $ \ theta _i \ left (t \ right) $ 값을 대입합니다.
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt \ right) $$
이것이 equation of FM wave.
변조 신호가 $ m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right) $이면 FM 파의 방정식은 다음과 같습니다.
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ beta \ sin \ left (2 \ pi f_mt \ right) \ right) $$
어디,
$ \ 베타 $ = modulation index $ = \ frac {\ Delta f} {f_m} = \ frac {k_fA_m} {f_m} $
FM 변조 주파수 (순간 주파수)와 일반 반송파 주파수의 차이는 다음과 같습니다. Frequency Deviation. $ \ Delta f $로 표시되며 $ k_f $ 및 $ A_m $의 곱과 같습니다.
FM은 다음과 같이 나눌 수 있습니다. Narrowband FM 과 Wideband FM 변조 지수 $ \ beta $의 값을 기반으로합니다.
협 대역 FM
다음은 협 대역 FM의 기능입니다.
이 주파수 변조는 광대역 FM에 비해 대역폭이 작습니다.
변조 지수 $ \ beta $는 작습니다. 즉, 1보다 작습니다.
스펙트럼은 반송파, 상부 측 파대 및 하부 측 파대로 구성됩니다.
이것은 경찰 무선, 구급차, 택시 등과 같은 이동 통신에 사용됩니다.
광대역 FM
다음은 Wideband FM의 기능입니다.
이 주파수 변조에는 무한한 대역폭이 있습니다.
변조 지수 $ \ beta $는 1보다 큽니다.
스펙트럼은 반송파와 주변에 위치한 무한한 수의 측 파대로 구성됩니다.
이것은 FM 라디오, TV 등과 같은 엔터테인먼트, 방송 응용 프로그램에 사용됩니다.
위상 변조
주파수 변조에서 반송파의 주파수는 다양합니다. 반면에Phase Modulation (PM), 반송파 신호의 위상은 변조 신호의 순간 진폭에 따라 달라집니다.
따라서 위상 변조에서 반송파 신호의 진폭과 주파수는 일정하게 유지됩니다. 이것은 다음 그림을 보면 더 잘 이해할 수 있습니다.
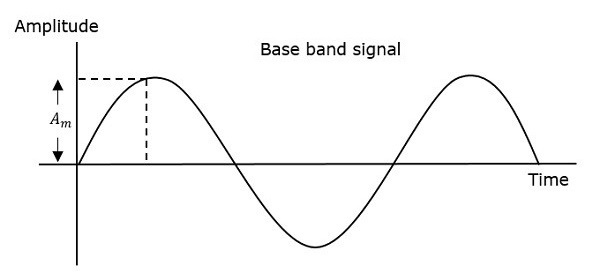

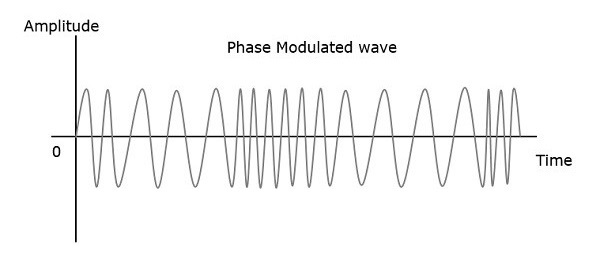
변조 된 파동의 위상에는 파동의 위상 변화가 발생할 수있는 무한 지점이 있습니다. 변조 신호의 순간 진폭은 반송파 신호의 위상을 변경합니다. 진폭이 양수이면 위상이 한 방향으로 변경되고 진폭이 음수이면 위상이 반대 방향으로 변경됩니다.
수학적 표현
위상 변조에서 순간 위상 $ \ phi_i $의 방정식은 다음과 같습니다.
$$ \ phi _i = k_p m \ left (t \ right) $$
어디,
$ k_p $는 위상 감도입니다.
$ m \ left (t \ right) $는 메시지 신호입니다.
각도 변조 파의 표준 방정식은 다음과 같습니다.
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ phi_i \ right) $$
위 방정식에서 $ \ phi_i $ 값을 대입합니다.
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + k_p m \ left (t \ right) \ right) $$
이것이 equation of PM wave.
변조 신호 $ m \ left (t \ right) = A_m \ cos \ left (2 \ pi f_mt \ right) $, PM 파의 방정식은 다음과 같습니다.
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ beta \ cos \ left (2 \ pi f_mt \ right) \ right) $$
어디,
$ \ 베타 $ = modulation index = $ \ 델타 \ phi = k_pA_m $
$ \ Delta \ phi $는 위상 편차입니다.
위상 변조는 이동 통신 시스템에 사용되며 주파수 변조는 주로 FM 방송에 사용됩니다.
이전 장에서 각도 변조에 사용 된 매개 변수에 대해 설명했습니다. 각 매개 변수에는 고유 한 공식이 있습니다. 이러한 공식을 사용하여 각각의 매개 변수 값을 찾을 수 있습니다. 이 장에서는 주파수 변조의 개념을 기반으로 몇 가지 문제를 해결해 보겠습니다.
문제 1
진폭이 5V이고 주파수가 2KHz 인 정현파 변조 파형이 주파수 감도가 40Hz / 볼트 인 FM 발생기에 적용됩니다. 주파수 편차, 변조 지수 및 대역폭을 계산합니다.
해결책
주어진 변조 신호의 진폭, $ A_m = 5V $
변조 신호의 주파수, $ f_m = 2 KHz $
주파수 감도, $ k_f = 40Hz / volt $
주파수 편차의 공식은 다음과 같습니다.
$$ \ 델타 f = k_f A_m $$
위 공식에서 $ k_f $ 및 $ A_m $ 값을 대체하십시오.
$$ \ 델타 f = 40 \ times 5 = 200Hz $$
따라서, frequency deviation, $ \ Delta f $는 $ 200Hz $입니다.
변조 지수의 공식은 다음과 같습니다.
$$ \ beta = \ frac {\ Delta f} {f_m} $$
위 공식에서 $ \ Delta f $ 및 $ f_m $ 값을 대체하십시오.
$$ \ beta = \ frac {200} {2 \ times 1000} = 0.1 $$
여기에서 modulation index, $ \ beta $는 0.1이며 1보다 작습니다. 따라서 Narrow Band FM입니다.
협 대역 FM의 대역폭 공식은 AM 파와 동일합니다.
$$ BW = 2f_m $$
위 공식에서 $ f_m $ 값을 대체하십시오.
$$ BW = 2 \ times 2K = 4KHz $$
따라서 bandwidth 협 대역 FM 파는 $ 4 KHz $입니다.
문제 2
FM 파는 $ s \ left (t \ right) = 20 \ cos \ left (8 \ pi \ times10 ^ 6t + 9 \ sin \ left (2 \ pi \ times 10 ^ 3 t \ right) \ right ) $. FM 파의 주파수 편차, 대역폭 및 전력을 계산합니다.
해결책
주어진 FM 파의 방정식은
$$ s \ left (t \ right) = 20 \ cos \ left (8 \ pi \ times10 ^ 6t + 9 \ sin \ left (2 \ pi \ times 10 ^ 3 t \ right) \ right) $$
우리는 FM 파의 표준 방정식을 다음과 같이 알고 있습니다.
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + \ beta \ sin \ left (2 \ pi f_mt \ right) \ right) $$
위의 두 방정식을 비교하여 다음 값을 얻습니다.
반송파 신호의 진폭, $ A_c = 20V $
반송파 신호의 주파수, $ f_c = 4 \ times 10 ^ 6 Hz = 4 MHz $
메시지 신호의 주파수, $ f_m = 1 \ times 10 ^ 3 Hz = 1KHz $
변조 지수, $ \ beta = 9 $
여기서 변조 지수의 값은 1보다 큽니다. 따라서Wide Band FM.
우리는 변조 지수의 공식을 다음과 같이 알고 있습니다.
$$ \ beta = \ frac {\ Delta f} {f_m} $$
위의 방정식을 다음과 같이 다시 정렬하십시오.
$$ \ 델타 = \ 베타 f_m $$
위의 방정식에서 $ \ beta $ 및 $ f_m $ 값을 대체하십시오.
$$ \ 델타 = 9 \ times 1K = 9KHz $$
따라서, frequency deviation, $ \ Delta f $는 $ 9 KHz $입니다.
광대역 FM 파의 대역폭 공식은 다음과 같습니다.
$$ BW = 2 \ 왼쪽 (\ beta +1 \ 오른쪽) f_m $$
위 공식에서 $ \ beta $ 및 $ f_m $ 값을 대체합니다.
$$ BW = 2 \ 왼쪽 (9 +1 \ 오른쪽) 1K = 20KHz $$
따라서 bandwidth 광대역 FM 파의 $ 20 KHz $
FM 파력의 공식은
$$ P_c = \ frac {{A_ {c}} ^ {2}} {2R} $$
$ R = 1 \ Omega $라고 가정하고 위의 방정식에서 $ A_c $ 값을 대체합니다.
$$ P = \ frac {\ left (20 \ right) ^ 2} {2 \ left (1 \ right)} = 200W $$
따라서 power FM 웨이브의 $ 200 $ watts.
이 장에서는 NBFM 및 WBFM 파를 생성하는 변조기에 대해 설명합니다. 먼저 NBFM의 생성에 대해 논의하겠습니다.
NBFM 생성
FM 파의 표준 방정식은
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt \ right) $$
$ \ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) \ cos \ left (2 \ pi k_f \ int m \ left (t \ right) dt \ right)-$
$ A_c \ sin \ left (2 \ pi f_ct \ right) \ sin \ left (2 \ pi k_f \ int m \ left (t \ right) dt \ right) $
NBFM의 경우
$$ \ 남음 | 2 \ pi k_f \ int m \ left (t \ right) dt \ right | <<1 $$
$ \ theta $가 매우 작을 때 $ \ cos \ theta \ approx 1 $ 및 $ \ sin \ theta \ approx 1 $을 알고 있습니다.
위의 관계를 사용하여 우리는 NBFM equation 같이
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) -A_c \ sin \ left (2 \ pi f_ct \ right) 2 \ pi k_f \ int m \ left (t \ 오른쪽) dt $$
NBFM 변조기의 블록 다이어그램은 다음 그림에 나와 있습니다.
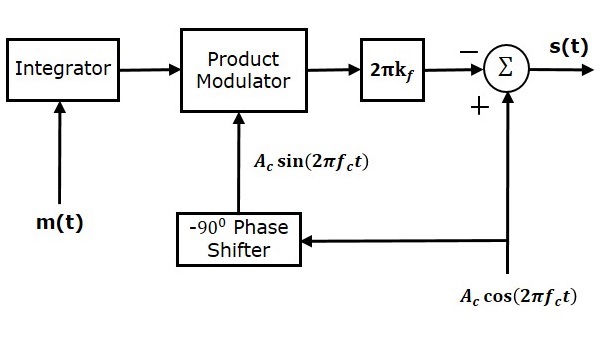
여기서 적분기는 변조 신호 $ m \ left (t \ right) $를 적분하는 데 사용됩니다. 반송파 신호 $ A_c \ cos \ left (2 \ pi f_ct \ right) $는 $ A_c \ sin \ left (2 \ pi f_ct \ right) $를 얻기 위해 $ -90 ^ 0 $만큼 이동 한 위상입니다. $ -90 ^ 0 $ 위상 시프터. 제품 변조기에는 두 개의 입력 $ \ int m \ left (t \ right) dt $ 및 $ A_c \ sin \ left (2 \ pi f_ct \ right) $가 있습니다. 이 두 입력의 곱인 출력을 생성합니다.
이것은 정방향 경로에 $ 2 \ pi k_f $ 블록을 배치하여 $ 2 \ pi k_f $와 더 곱해집니다. 여름 블록에는 NBFM 방정식의 두 항에 불과한 두 개의 입력이 있습니다. 양수 및 음수 부호는 반송파 신호에 할당되고 다른 항은 여름 블록의 입력에 할당됩니다. 마지막으로 여름 블록은 NBFM 파를 생성합니다.
WBFM의 생성
다음 두 가지 방법은 WBFM 파를 생성합니다.
- 직접 방법
- 간접 방법
직접 방법
이 방법은 광대역 FM 파를 직접 생성하기 때문에 Direct Method라고합니다. 이 방법에서는 VCO (Voltage Controlled Oscillator)를 사용하여 WBFM을 생성합니다. VCO는 주파수가 입력 신호 전압에 비례하는 출력 신호를 생성합니다. 이것은 FM 파의 정의와 유사합니다. WBFM 웨이브 생성의 블록 다이어그램은 다음 그림에 나와 있습니다.

여기서 변조 신호 $ m \ left (t \ right) $는 전압 제어 발진기 (VCO)의 입력으로 적용됩니다. VCO는 WBFM에 불과한 출력을 생성합니다.
$$ f_i \ : \ alpha \ : m \ left (t \ right) $$
$$ \ 오른쪽 화살표 f_i = f_c + k_fm \ 왼쪽 (t \ 오른쪽) $$
어디,
$ f_i $는 WBFM 파의 순간 주파수입니다.
간접 방법
이 방법은 광대역 FM 파를 간접적으로 생성하기 때문에 간접 방법이라고합니다. 즉, 먼저 NBFM 파를 생성 한 다음 주파수 배율기를 사용하여 WBFM 파를 얻습니다. WBFM 파형 생성의 블록 다이어그램은 다음 그림에 나와 있습니다.

이 블록 다이어그램은 주로 두 단계로 구성됩니다. 첫 번째 단계에서는 NBFM 변조기를 사용하여 NBFM 파가 생성됩니다. 이 장의 시작 부분에서 NBFM 변조기의 블록 다이어그램을 보았습니다. 우리는 NBFM 파의 변조 지수가 1 미만이라는 것을 알고 있습니다. 따라서 FM 파의 필요한 변조 지수 (하나 이상)를 얻으려면 주파수 배율 값을 적절하게 선택하십시오.
Frequency multiplier는 주파수가 입력 신호 주파수의 'n'배인 출력 신호를 생성하는 비선형 장치입니다. 여기서 'n'은 곱셈 계수입니다.
변조 지수 $ \ beta $가 1 미만인 NBFM 파형이 주파수 배율기의 입력으로 적용되면 주파수 배율기는 변조 지수가 'n'x $ \ beta $이고 주파수도 'n 인 출력 신호를 생성합니다. '배 WBFM 파의 주파수.
때로는 FM 파의 주파수 편차와 변조 지수를 높이기 위해 여러 단계의 주파수 곱셈기 및 믹서가 필요할 수 있습니다.
이 장에서는 FM 파를 복조하는 복조기에 대해 논의하겠습니다. 다음 두 가지 방법은 FM 파를 복조합니다.
- 주파수 판별 방법
- 위상 차별 방법
주파수 식별 방법
우리는 FM 파의 방정식이
$$ s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt \ right) $$
'에 대해 위의 방정식을 미분t'.
$$ \ frac {ds \ left (t \ right)} {dt} = -A_c \ left (2 \ pi f_c + 2 \ pi k_fm \ left (t \ right) \ right) \ sin \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt \ right) $$
$-\ sin \ theta $를 $ \ sin \ left (\ theta -180 ^ 0 \ right) $로 쓸 수 있습니다.
$$ \ Rightarrow \ frac {ds (t)} {dt} = A_c \ left (2 \ pi f_c + 2 \ pi k_fm \ left (t \ right) \ right) \ sin \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt-180 ^ 0 \ right) $$
$$ \ Rightarrow \ frac {ds (t)} {dt} = A_c \ left (2 \ pi f_c \ right) \ left [1+ \ left (\ frac {k_f} {k_c} \ right) m \ left ( t \ right) \ right] \ sin \ left (2 \ pi f_ct + 2 \ pi k_f \ int m \ left (t \ right) dt-180 ^ 0 \ right) $$
위의 방정식에서 진폭 항은 AM 파의 포락선과 유사하고 각도 항은 FM 파의 각도와 유사합니다. 여기서 우리의 요구 사항은 변조 신호 $ m \ left (t \ right) $입니다. 따라서 우리는 AM 파의 포락선에서 그것을 복구 할 수 있습니다.
다음 그림은 주파수 판별 방법을 사용하는 FM 복조기의 블록 다이어그램을 보여줍니다.

이 블록 다이어그램은 미분기와 포락선 감지기로 구성됩니다. 미분기는 FM 파를 AM 파와 FM 파의 조합으로 변환하는 데 사용됩니다. 즉, FM 파의 주파수 변화를 AM 파의 해당 전압 (진폭) 변화로 변환합니다. 우리는 봉투 감지기의 작동을 알고 있습니다. 그것은 변조 신호에 불과한 AM 파의 복조 된 출력을 생성합니다.
위상 차별 방법
다음 그림은 위상 판별 방법을 사용하는 FM 복조기의 블록 다이어그램을 보여줍니다.

이 블록 다이어그램은 승수, 저역 통과 필터 및 VCO (Voltage Controlled Oscillator)로 구성됩니다. VCO는 출력 신호 $ v \ left (t \ right) $를 생성하는데, 주파수는 입력 신호 전압 $ d \ left (t \ right) $에 비례합니다. 처음에 $ d \ left (t \ right) $ 신호가 0이면 VCO를 조정하여 캐리어 주파수와 $ -90 ^ 0 $ 위상 편이를 갖는 출력 신호 $ v \ left (t \ right) $를 생성합니다. 반송파 신호와 관련하여.
FM 웨이브 $ s \ left (t \ right) $ 및 VCO 출력 $ v \ left (t \ right) $는 승수의 입력으로 적용됩니다. 승수는 고주파수 성분과 저주파 성분을 가진 출력을 생성합니다. 저역 통과 필터는 고주파 성분을 제거하고 저주파 성분 만 출력으로 생성합니다.
이 저주파 성분에는 용어 관련 위상차 만 포함되어 있습니다. 따라서 우리는 저역 통과 필터의 출력에서 변조 신호 $ m \ left (t \ right) $를 얻습니다.
Multiplexing공유 매체를 통해 여러 신호를 하나의 신호로 결합하는 프로세스입니다. 아날로그 신호가 다중화 된 경우 다음과 같이 호출됩니다.analog multiplexing. 마찬가지로 디지털 신호가 다중화되면 다음과 같이 호출됩니다.digital multiplexing.
멀티플렉싱은 전화 통신에서 처음 개발되었습니다. 여러 신호가 결합되어 단일 케이블을 통해 전송되었습니다. 멀티플렉싱 프로세스는 통신 채널을 여러 개의 논리 채널로 분할하여 서로 다른 메시지 신호 또는 전송할 데이터 스트림에 대해 각각을 할당합니다. 멀티플렉싱을 수행하는 장치는 다음과 같이 호출 할 수 있습니다.Multiplexer 또는 MUX.
그 반대 과정, 즉 하나에서 채널 수를 추출하는 과정이 수신자에서 수행되는 과정을 다음과 같이 호출합니다. de-multiplexing. 디 멀티플렉싱을 수행하는 장치는 다음과 같이 호출 할 수 있습니다.de-multiplexer 또는 DEMUX.
다음 그림은 MUX 및 DEMUX의 개념을 보여줍니다. 주요 용도는 통신 분야입니다.

멀티플렉서 유형
주로 아날로그와 디지털의 두 가지 유형의 멀티플렉서가 있습니다. FDM (Frequency Division Multiplexing), WDM (Wavelength Division Multiplexing) 및 TDM (Time Division Multiplexing)으로 더 나뉩니다. 다음 그림은이 분류에 대한 자세한 아이디어를 제공합니다.
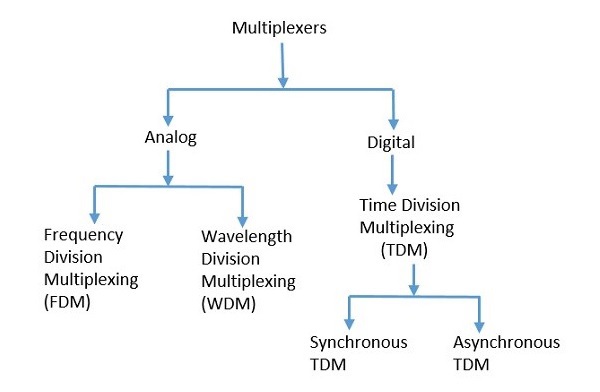
여러 유형의 다중화 기술이 있습니다. 그 중에서 위의 그림에 언급 된 일반 분류의 주요 유형이 있습니다. 개별적으로 살펴 보겠습니다.
아날로그 멀티플렉싱
아날로그 멀티플렉싱 기술에 사용되는 신호는 본질적으로 아날로그입니다. 아날로그 신호는 주파수 (FDM) 또는 파장 (WDM)에 따라 다중화됩니다.
주파수 분할 다중화
아날로그 멀티플렉싱에서 가장 많이 사용되는 기술은 FDM (Frequency Division Multiplexing)입니다. 이 기술은 다양한 주파수를 사용하여 데이터 스트림을 결합하여 통신 매체에 단일 신호로 전송합니다.
Example − 단일 케이블을 통해 여러 채널을 전송하는 기존 TV 송신기는 FDM을 사용합니다.
파장 분할 다중화
WDM (Wavelength Division Multiplexing)은 서로 다른 파장의 많은 데이터 스트림이 광 스펙트럼으로 전송되는 아날로그 기술입니다. 파장이 증가하면 신호의 주파수가 감소합니다. MUX의 출력과 DEMUX의 입력에 서로 다른 파장을 단일 라인으로 바꿀 수있는 프리즘을 사용할 수 있습니다.
Example − 광섬유 통신은 WDM 기술을 사용하여 서로 다른 파장을 하나의 빛으로 병합하여 통신합니다.
디지털 멀티플렉싱
디지털이라는 용어는 정보의 개별 비트를 나타냅니다. 따라서 사용 가능한 데이터는 개별적인 프레임 또는 패킷의 형태입니다.
시분할 다중화
TDM (시분할 다중화)에서 시간 프레임은 슬롯으로 나뉩니다. 이 기술은 각 메시지에 대해 하나의 슬롯을 할당하여 단일 통신 채널을 통해 신호를 전송하는 데 사용됩니다.
TDM (Time Division Multiplexing)은 동기식 TDM과 비동기식 TDM으로 분류 할 수 있습니다.
동기식 TDM
동기식 TDM에서 입력은 프레임에 연결됩니다. 연결 수가 'n'인 경우 프레임은 'n'시간 슬롯으로 나뉩니다. 각 입력 라인에 하나의 슬롯이 할당됩니다.
이 기술에서 샘플링 속도는 모든 신호에 대해 공통이므로 동일한 클럭 입력이 제공됩니다. MUX는same slot 항상 각 장치에.
비동기 TDM
비동기식 TDM에서는 샘플링 속도가 신호마다 다르며 공통 클록이 필요하지 않습니다. 시간 슬롯에 할당 된 장치가 아무것도 전송하지 않고 유휴 상태 인 경우 해당 슬롯은allotted to another 동기와 달리 장치
이 유형의 TDM은 비동기 전송 모드 네트워크에서 사용됩니다.
디멀티플렉서
디멀티플렉서는 단일 소스를 여러 대상에 연결하는 데 사용됩니다. 이 과정은 멀티플렉싱의 역 과정입니다. 앞서 언급했듯이 대부분 수신기에서 사용됩니다. DEMUX에는 많은 응용 프로그램이 있습니다. 통신 시스템의 수신기에 사용됩니다. 컴퓨터의 산술 및 논리 장치에서 전원을 공급하고 통신을 전달하는 데 사용됩니다.
디멀티플렉서는 직렬-병렬 변환기로 사용됩니다. 직렬 데이터는 정기적으로 DEMUX에 입력으로 제공되며 역다 중화기의 출력을 제어하기 위해 카운터가 부착됩니다.
멀티플렉서와 디멀티플렉서는 송신기 및 수신기 섹션 모두에서 통신 시스템에서 중요한 역할을합니다.
모든 통신 시스템에서 신호를 전송하는 동안 또는 신호를 수신하는 동안 일부 원하지 않는 신호가 통신에 도입되어 수신기를 불쾌하게 만들고 통신 품질에 의문을 제기합니다. 이러한 방해는Noise.
소음이란?
소음은 unwanted signal, 이는 원래 메시지 신호를 방해하고 메시지 신호의 매개 변수를 손상시킵니다. 통신 프로세스의 이러한 변경으로 인해 메시지가 변경됩니다. 대부분의 경우 채널이나 수신기에 들어갑니다.
노이즈 신호는 다음 그림을 보면 이해할 수 있습니다.

따라서 노이즈는 패턴이없고 일정한 주파수 나 진폭이없는 신호라는 것을 알 수 있습니다. 그것은 매우 무작위적이고 예측할 수 없습니다. 완전히 제거 할 수는 없지만 일반적으로이를 줄이기위한 조치가 취해집니다.
노이즈의 가장 일반적인 예는 다음과 같습니다.
라디오 수신기의 히스 사운드
전화 대화 중 버즈 소리
텔레비전 수신기 등의 깜박임
소음의 유형
노이즈 분류는 소스의 유형, 표시되는 효과 또는 수신기와의 관계 등에 따라 수행됩니다.
소음이 발생하는 두 가지 주요 방법이 있습니다. 하나는 일부를 통해external source 다른 하나는 internal source, 수신자 섹션 내.
외부 소스
이 소음은 외부 소스에 의해 생성되며 일반적으로 통신 매체 또는 채널에서 발생할 수 있습니다. 이 소음은 완전히 제거 할 수 없습니다. 가장 좋은 방법은 잡음이 신호에 영향을주지 않도록하는 것입니다.
예
이러한 유형의 소음에 대한 가장 일반적인 예는 다음과 같습니다.
대기 소음 (대기의 불규칙성).
태양 소음 및 우주 소음과 같은 외계 소음.
산업 소음.
내부 소스
이 소음은 작동하는 동안 수신기 구성 요소에서 생성됩니다. 연속적인 기능으로 인해 회로의 구성 요소는 몇 가지 유형의 노이즈를 생성 할 수 있습니다. 이 소음은 정량화 할 수 있습니다. 적절한 수신기 설계는이 내부 잡음의 영향을 낮출 수 있습니다.
Examples
이러한 유형의 소음에 대한 가장 일반적인 예는 다음과 같습니다.
열 교반 소음 (Johnson 소음 또는 전기 소음)
샷 노이즈 (전자와 정공의 무작위 이동으로 인해)
이동 시간 소음 (전환 중)
기타 노이즈는 깜박임, 저항 효과 및 믹서 생성 노이즈 등을 포함하는 또 다른 유형의 노이즈입니다.
소음의 영향
소음은 시스템 성능에 영향을 미치는 불편한 기능입니다. 다음은 소음의 영향입니다.
소음은 시스템의 작동 범위를 제한합니다.
잡음은 증폭기로 증폭 할 수있는 가장 약한 신호에 간접적으로 제한을 둡니다. 믹서 회로의 발진기는 잡음 때문에 주파수를 제한 할 수 있습니다. 시스템의 작동은 회로의 작동에 따라 다릅니다. 잡음은 수신기가 처리 할 수있는 가장 작은 신호를 제한합니다.
잡음은 수신기의 감도에 영향을 미칩니다.
감도는 지정된 품질 출력을 얻기 위해 필요한 최소 입력 신호 량입니다. 노이즈는 수신기 시스템의 감도에 영향을 미치며 결국 출력에 영향을 미칩니다.
이 장에서는 수신기에서 복조되는 다양한 변조 파의 신호 대 잡음비와 성능 지수를 계산해 보겠습니다.
신호 대 잡음비
Signal-to-Noise Ratio (SNR)신호 전력 대 잡음 전력의 비율입니다. SNR 값이 높을수록 수신 된 출력의 품질이 높아집니다.
다음 공식을 사용하여 여러 지점에서 신호 대 잡음비를 계산할 수 있습니다.
Input SNR = $ \ left (SNR \ right) _I = \ frac {Average \ : \ : power \ : \ : of \ : \ : modulating \ : \ : signal} {Average \ : \ : power \ : \ : of \ : \ : 노이즈 \ : \ : at \ : \ : input} $
Output SNR = $ \ left (SNR \ right) _O = \ frac {Average \ : \ : power \ : \ : of \ : \ : demodulated \ : \ : signal} {Average \ : \ : power \ : \ : of \ : \ : 노이즈 \ : \ : at \ : \ : 출력} $
Channel SNR = $ \ left (SNR \ right) _C = \ frac {Average \ : \ : power \ : \ : of \ : \ : modulated \ : \ : signal} {Average \ : \ : power \ : \ : of \ : \ : 노이즈 \ : \ : in \ : \ : message \ : \ : bandwidth} $
공로의 그림
출력 SNR과 입력 SNR의 비율은 다음과 같이 표현할 수 있습니다. Figure of Merit. 다음과 같이 표시됩니다.F. 장치의 성능을 설명합니다.
$$ F = \ frac {\ 왼쪽 (SNR \ 오른쪽) _O} {\ 왼쪽 (SNR \ 오른쪽) _I} $$
수신기의 장점은 다음과 같습니다.
$$ F = \ frac {\ 왼쪽 (SNR \ 오른쪽) _O} {\ 왼쪽 (SNR \ 오른쪽) _C} $$
수신기의 경우 채널이 입력이기 때문입니다.
AM 시스템의 SNR 계산
잡음을 분석하기 위해 AM 시스템의 다음 수신기 모델을 고려하십시오.

우리는 진폭 변조 (AM) 파가
$$ s \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$
$$ \ Rightarrow s \ left (t \ right) = A_c \ cos \ left (2 \ pi f_ct \ right) + A_ck_am \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) $$
AM 파의 평균 전력은
$$ P_s = \ left (\ frac {A_c} {\ sqrt {2}} \ right) ^ 2 + \ left (\ frac {A_ck_am \ left (t \ right)} {\ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2}} {2} + \ frac {{A_ {c}} ^ {2} {k_ {a}} ^ {2} P} {2} $ $
$$ \ Rightarrow P_s = \ frac {{A_ {c}} ^ {2} \ left (1+ {k_ {a}} ^ {2} P \ right)} {2} $$
메시지 대역폭의 평균 잡음 전력은
$$ P_ {nc} = WN_0 $$
대체,이 값은 channel SNR 공식
$$ \ left (SNR \ right) _ {C, AM} = \ frac {Average \ : \ : Power \ : \ : of \ : \ : AM \ : \ : Wave} {Average \ : \ : Power \ : \ : / \ : \ : 노이즈 \ : \ : \ : \ : 메시지 \ : \ : 대역폭} $$
$$ \ Rightarrow \ left (SNR \ right) _ {C, AM} = \ frac {{A_ {c}} ^ {2} \ left (1+ {k_ {a}} ^ {2} \ right) P } {2WN_0} $$
어디,
P 메시지 신호의 힘 = $ \ frac {{A_ {m}} ^ {2}} {2} $
W 메시지 대역폭입니다.
위 그림과 같이 대역 통과 노이즈가 채널에서 AM 파와 혼합되었다고 가정합니다. 이 조합은 AM 복조기의 입력에 적용됩니다. 따라서 AM 복조기의 입력은 다음과 같습니다.
$$ v \ 왼쪽 (t \ 오른쪽) = s \ 왼쪽 (t \ 오른쪽) + n \ 왼쪽 (t \ 오른쪽) $$
$ \ Rightarrow v \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) + $
$ \ left [n_1 \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right)-n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ right] $
$ \ Rightarrow v \ left (t \ right) = \ left [A_c + A_ck_am \ left (t \ right) + n_1 \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right)- n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) $
$ n_I \ left (t \ right) $ 및 $ n_Q \ left (t \ right) $는 잡음의 위상 및 직교 위상 성분입니다.
AM 복조기의 출력은 위 신호의 포락선에 불과합니다.
$$ d \ left (t \ right) = \ sqrt {\ left [A_c + A_cK_am \ left (t \ right) + n_I \ left (t \ right) \ right] ^ 2 + \ left (n_Q \ left (t \ 오른쪽) \ 오른쪽) ^ 2} $$
$$ \ 오른쪽 화살표 d \ 왼쪽 (t \ 오른쪽) \ 대략 A_c + A_ck_am \ 왼쪽 (t \ 오른쪽) + n_1 \ 왼쪽 (t \ 오른쪽) $$
복조 된 신호의 평균 전력은 다음과 같습니다.
$$ P_m = \ left (\ frac {A_ck_am \ left (t \ right)} {\ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2} {k_ {a} } ^ {2} P} {2} $$
출력에서 평균 잡음 전력은
$$ P_no = WN_0 $$
대체,이 값은 output SNR 공식.
$$ \ left (SNR \ right) _ {O, AM} = \ frac {Average \ : \ : Power \ : \ : of \ : \ : 복조 \ : \ : 신호} {Average \ : \ : Power \ : \ : / \ : \ : 노이즈 \ : \ : \ : \ : 출력} $$
$$ \ Rightarrow \ left (SNR \ right) _ {O, AM} = \ frac {{A_ {c}} ^ {2} {k_ {a}} ^ {2} P} {2WN_0} $$
대체, 값 Figure of merit AM 수신기 공식의.
$$ F = \ frac {\ 왼쪽 (SNR \ 오른쪽) _ {O, AM}} {\ 왼쪽 (SNR \ 오른쪽) _ {C, AM}} $$
$$ \ Rightarrow F = \ left (\ frac {{A_ {c} ^ {2}} {k_ {a} ^ {2}} P} {2WN_0} \ right) / \ left (\ frac {{A_ { c}} ^ {2} \ left (1+ {k_ {a}} ^ {2} \ right) P} {2WN_0} \ right) $$
$$ \ Rightarrow F = \ frac {{K_ {a}} ^ {2} P} {1+ {K_ {a}} ^ {2} P} $$
따라서 AM 수신기의 성능 지수는 1 미만입니다.
DSBSC 시스템의 SNR 계산
잡음을 분석하기 위해 DSBSC 시스템의 다음 수신기 모델을 고려하십시오.

우리는 DSBSC 변조 파가
$$ s \ left (t \ right) = A_cm \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) $$
DSBSC 변조 파의 평균 전력은 다음과 같습니다.
$$ P_s = \ left (\ frac {A_cm \ left (t \ right)} {\ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2} P} {2} $$
메시지 대역폭의 평균 잡음 전력은
$$ P_ {nc} = WN_0 $$
대체,이 값은 channel SNR 공식.
$$ \ left (SNR \ right) _ {C, DSBSC} = \ frac {Average \ : \ : Power \ : \ : of \ : \ : DSBSC \ : \ : modulated \ : \ : wave} {Average \ : \ : 전원 \ : \ : of \ : \ : 노이즈 \ : \ : in \ : \ : 메시지 \ : \ : 대역폭} $$
$$ \ Rightarrow \ left (SNR \ right) _ {C, DSBSC} = \ frac {{A_ {c}} ^ {2} P} {2WN_0} $$
위 그림과 같이 대역 통과 잡음이 채널에서 DSBSC 변조 파와 혼합되었다고 가정합니다. 이 조합은 제품 변조기에 대한 입력 중 하나로 적용됩니다. 따라서이 제품 변조기의 입력은
$$ v_1 \ 왼쪽 (t \ 오른쪽) = s \ 왼쪽 (t \ 오른쪽) + n \ 왼쪽 (t \ 오른쪽) $$
$$ \ Rightarrow v_1 \ left (t \ right) = A_cm \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) + \ left [n_I \ left (t \ right) \ cos \ left ( 2 \ pi f_ct \ right)-n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ right] $$
$$ \ Rightarrow v_1 \ left (t \ right) = \ left [A_cm \ left (t \ right) + n_I \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) $$
로컬 오실레이터는 캐리어 신호 $ c \ left (t \ right) = \ cos \ left (2 \ pi f_ct \ right) $를 생성합니다. 이 신호는 제품 변조기에 대한 또 다른 입력으로 적용됩니다. 따라서 제품 변조기는 $ v_1 \ left (t \ right) $ 및 $ c \ left (t \ right) $의 곱인 출력을 생성합니다.
$$ v_2 \ 왼쪽 (t \ 오른쪽) = v_1 \ 왼쪽 (t \ 오른쪽) c \ 왼쪽 (t \ 오른쪽) $$
위 방정식에서 $ v_1 \ left (t \ right) $ 및 $ c \ left (t \ right) $ 값을 대체하십시오.
$$ \ Rightarrow v_2 \ left (t \ right) = \ left (\ left [A_cm \ left (t \ right) + n_I \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right )-n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ right) \ cos \ left (2 \ pi f_ct \ right) $$
$$ \ Rightarrow v_2 \ left (t \ right) = \ left [A_c m \ left (t \ right) + n_I \ left (t \ right) \ right] \ cos ^ 2 \ left (2 \ pi f_ct \ right ) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ cos \ left (2 \ pi f_ct \ right) $$
$$ \ Rightarrow v_2 \ left (t \ right) = \ left [A_c m \ left (t \ right) + n_I \ left (t \ right) \ right] \ left (\ frac {1+ \ cos \ left ( 4 \ pi f_ct \ right)} {2} \ right) -n_Q \ left (t \ right) \ frac {\ sin \ left (4 \ pi f_ct \ right)} {2} $$
위의 신호가 로우 패스 필터의 입력으로 적용되면 로우 패스 필터의 출력을 다음과 같이 얻을 수 있습니다.
$$ d \ left (t \ right) = \ frac {\ left [A_c m \ left (t \ right) + n_I \ left (t \ right) \ right]} {2} $$
복조 된 신호의 평균 전력은 다음과 같습니다.
$$ P_m = \ left (\ frac {A_cm \ left (t \ right)} {2 \ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2} P} {8 } $$
출력에서 평균 잡음 전력은
$$ P_ {no} = \ frac {WN_0} {4} $$
대체,이 값은 output SNR 공식.
$$ \ left (SNR \ right) _ {O, DSBSC} = \ frac {Average \ : \ : Power \ : \ : of \ : \ : 복조 \ : \ : 신호} {Average \ : \ : Power \ : \ : / \ : \ : 노이즈 \ : \ : \ : \ : 출력} $$
$$ \ Rightarrow \ left (SNR \ right) _ {O, DSBSC} = \ left (\ frac {{A_ {c}} ^ {2} P} {8} \ right) / \ left (\ frac {WN_0 } {4} \ right) = \ frac {{A_ {c}} ^ {2} P} {2WN_0} $$
대체, 값 Figure of merit DSBSC 수신기 공식의.
$$ F = \ frac {\ 왼쪽 (SNR \ 오른쪽) _ {O, DSBSC}} {\ 왼쪽 (SNR \ 오른쪽) _ {C, DSBSC}} $$
$$ \ 오른쪽 화살표 F = \ left (\ frac {{A_ {c}} ^ {2} P} {2WN_0} \ right) / \ left (\ frac {{A_ {c}} ^ {2} P} { 2WN_0} \ 오른쪽) $$
$$ \ 오른쪽 화살표 F = 1 $$
따라서 DSBSC 수신기의 성능 지수는 1입니다.
SSBSC 시스템의 SNR 계산
잡음을 분석하기 위해 SSBSC 시스템의 다음 수신기 모델을 고려하십시오.
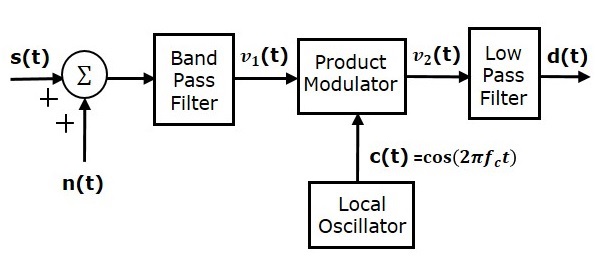
우리는 더 낮은 측 파대를 갖는 SSBSC 변조 파가
$$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $$
SSBSC 변조 파의 평균 전력은 다음과 같습니다.
$$ P_s = \ left (\ frac {A_mA_c} {2 \ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8} $$
메시지 대역폭의 평균 잡음 전력은
$$ P_ {nc} = WN_0 $$
대체,이 값은 channel SNR 공식.
$$ \ left (SNR \ right) _ {C, SSBSC} = \ frac {Average \ : \ : Power \ : \ : of \ : \ : SSBSC \ : \ : modulated \ : \ : wave} {Average \ : \ : 전원 \ : \ : of \ : \ : 노이즈 \ : \ : in \ : \ : 메시지 \ : \ : 대역폭} $$
$$ \ Rightarrow \ left (SNR \ right) _ {C, SSBSC} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} $$
위 그림과 같이 대역 통과 잡음이 채널에서 SSBSC 변조 파와 혼합되었다고 가정합니다. 이 조합은 제품 변조기에 대한 입력 중 하나로 적용됩니다. 따라서이 제품 변조기의 입력은
$$ v_1 \ 왼쪽 (t \ 오른쪽) = s \ 왼쪽 (t \ 오른쪽) + n \ 왼쪽 (t \ 오른쪽) $$
$$ v_1 \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] + n_I \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) $$
국부 발진기는 반송파 신호 $ c \ left (t \ right) = \ cos \ left (2 \ pi f_ct \ right) $를 생성합니다. 이 신호는 제품 변조기에 대한 또 다른 입력으로 적용됩니다. 따라서 제품 변조기는 $ v_1 \ left (t \ right) $ 및 $ c \ left (t \ right) $의 곱인 출력을 생성합니다.
$$ v_2 \ 왼쪽 (t \ 오른쪽) = v_1 \ 왼쪽 (t \ 오른쪽) c \ 왼쪽 (t \ 오른쪽) $$
위 방정식에서 $ v_1 \ left (t \ right) $ 및 $ c \ left (t \ right) $ 값을 대입합니다.
$ \ Rightarrow v_2 (t) = (\ frac {A_mA_c} {2} \ cos [2 \ pi (f_c-f_m) t] + n_I (t) \ cos (2 \ pi f_ct)-$
$ n_Q (t) \ sin (2 \ pi f_ct)) \ cos (2 \ pi f_ct) $
$ \ Rightarrow v_2 \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] \ cos \ left (2 \ pi f_ct \ 오른쪽) + $
$ n_I \ left (t \ right) \ cos ^ 2 \ left (2 \ pi f_ct \ right) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ cos \ left (2 \ pi f_ct \ 오른쪽) $
$ \ Rightarrow v_2 \ left (t \ right) = \ frac {A_mA_c} {4} \ left \ {\ cos \ left [2 \ pi \ left (2f_c-f_m \ right) t \ right] + \ cos \ left (2 \ pi f_mt \ right) \ right \} + $
$ n_I \ left (t \ right) \ left (\ frac {1+ \ cos \ left (4 \ pi f_ct \ right)} {2} \ right)-n_Q \ left (t \ right) \ frac {\ sin \ 왼쪽 (4 \ pi f_ct \ 오른쪽)} {2} $
위의 신호가 로우 패스 필터의 입력으로 적용되면 로우 패스 필터의 출력을 다음과 같이 얻을 수 있습니다.
$$ d \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left (2 \ pi f_mt \ right) + \ frac {n_I \ left (t \ right)} {2} $$
복조 된 신호의 평균 전력은 다음과 같습니다.
$$ P_m = \ left (\ frac {A_mA_c} {4 \ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {32} $$
출력에서 평균 잡음 전력은
$$ P_ {no} = \ frac {WN_0} {4} $$
대체,이 값은 output SNR 공식
$$ \ left (SNR \ right) _ {O, SSBSC} = \ frac {Average \ : \ : Power \ : \ : of \ : \ : 복조 \ : \ : signal} {Average \ : \ : Power \ : \ : / \ : \ : 노이즈 \ : \ : \ : \ : 출력} $$
$$ \ Rightarrow \ left (SNR \ right) _ {O, SSBSC} = \ left (\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {32} \ right ) / \ left (\ frac {WN_0} {4} \ right) = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} $$
대체, 값 Figure of merit SSBSC 수신기 공식
$$ F = \ frac {\ 왼쪽 (SNR \ 오른쪽) _ {O, SSBSC}} {\ 왼쪽 (SNR \ 오른쪽) _ {C, SSBSC}} $$
$$ F = \ left (\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} \ right) / \ left (\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} \ right) $$
$$ F = 1 $$
따라서 SSBSC 수신기의 성능 지수는 1입니다.
송신기 섹션 끝에있는 안테나는 변조 된 파를 전송합니다. 이 장에서는 AM 및 FM 송신기에 대해 설명하겠습니다.
AM 송신기
AM 송신기는 오디오 신호를 입력으로 받아 안테나에 진폭 변조 파를 출력으로 전달합니다. AM 송신기의 블록 다이어그램은 다음 그림에 나와 있습니다.

AM 송신기의 작동은 다음과 같이 설명 할 수 있습니다.
마이크 출력의 오디오 신호는 전치 증폭기로 전송되어 변조 신호의 레벨을 높입니다.
RF 발진기는 반송파 신호를 생성합니다.
변조 및 반송파 신호는 모두 AM 변조기로 전송됩니다.
전력 증폭기는 AM 파의 전력 레벨을 높이는 데 사용됩니다. 이 파동은 마지막으로 안테나로 전달되어 전송됩니다.
FM 송신기
FM 송신기는 오디오 신호를 입력으로 받아 안테나에 FM 파를 출력으로 전달하는 전체 장치입니다. FM 송신기의 블록 다이어그램은 다음 그림에 나와 있습니다.

FM 송신기의 작동은 다음과 같이 설명 할 수 있습니다.
마이크 출력의 오디오 신호는 전치 증폭기로 전송되어 변조 신호의 레벨을 높입니다.
이 신호는 노이즈를 필터링하고 신호 대 노이즈 비율을 개선하는 프리 엠 퍼시스 네트워크 역할을하는 하이 패스 필터로 전달됩니다.
이 신호는 FM 변조기 회로로 더 전달됩니다.
발진기 회로는 변조 신호와 함께 변조기로 전송되는 고주파 반송파를 생성합니다.
작동 주파수를 높이기 위해 여러 단계의 주파수 배율기가 사용됩니다. 그럼에도 불구하고 신호의 힘은 전송하기에 충분하지 않습니다. 따라서 RF 전력 증폭기는 변조 된 신호의 전력을 높이기 위해 마지막에 사용됩니다. 이 FM 변조 출력은 최종적으로 전송 될 안테나로 전달됩니다.
수신기 섹션의 시작 부분에있는 안테나는 변조 된 파를 수신합니다. 먼저 수신기의 요구 사항에 대해 논의하겠습니다.
수신자의 요구 사항
AM 수신기는 AM 파를 수신하고 엔벨로프 감지기를 사용하여 복조합니다. 마찬가지로 FM 수신기는 FM 전파를 수신하여 주파수 식별 방법을 사용하여 복조합니다. 다음은 AM 및 FM 수신기의 요구 사항입니다.
비용 효율적이어야합니다.
해당 변조 파를 수신해야합니다.
수신기는 원하는 방송국을 튜닝하고 증폭 할 수 있어야합니다.
원치 않는 방송국을 거부하는 기능이 있어야합니다.
반송파 신호 주파수에 관계없이 모든 스테이션 신호에 대해 복조를 수행해야합니다.
이러한 요구 사항이 충족 되려면 튜너 회로와 믹서 회로가 매우 효과적이어야합니다. RF 믹싱 절차는 흥미로운 현상입니다.
RF 믹싱
RF 혼합 장치는 Intermediate Frequency (IF) 신호를 효과적으로 처리하기 위해 수신 된 신호가 변환됩니다.
RF Mixer는 수신기에서 중요한 단계입니다. 하나의 신호 레벨이 다른 신호의 레벨에 영향을 미치는 다른 주파수의 두 신호를 가져와 결과적인 혼합 출력을 생성합니다. 입력 신호와 결과 믹서 출력은 다음 그림에 나와 있습니다.
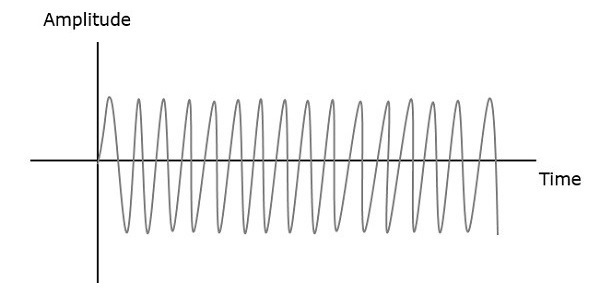
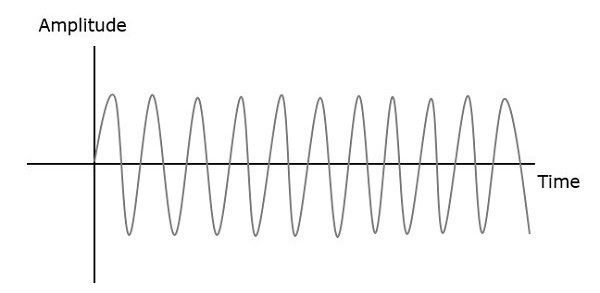

첫 번째 및 두 번째 신호 주파수를 $ f_1 $ 및 $ f_2 $로 지정합니다. 이 두 신호가 RF 믹서의 입력으로 적용되면 $ f_1 + f_2 $ 및 $ f_1-f_2 $의 주파수를 갖는 출력 신호가 생성됩니다.
이것이 주파수 영역에서 관찰되면 패턴은 다음 그림과 같습니다.

이 경우 $ f_1 $는 $ f_2 $보다 큽니다. 따라서 결과 출력에는 $ f_1 + f_2 $ 및 $ f_1-f_2 $ 주파수가 있습니다. 마찬가지로 $ f_2 $가 $ f_1 $보다 크면 결과 출력의 주파수는 $ f_1 + f_2 $ 및 $ f_1-f_2 $입니다.
AM 수신기
AM 수퍼 헤테로 다인 수신기는 진폭 변조 파를 입력으로 받아 원래 오디오 신호를 출력으로 생성합니다. Selectivity 특정 신호를 선택하고 다른 신호를 거부하는 능력입니다. Sensitivity 가장 낮은 전력 레벨에서 RF 신호를 감지하고 복조하는 용량입니다.
라디오 아마추어는 초기 라디오 수신기입니다. 그러나 감도와 선택성이 떨어지는 단점이 있습니다. 이러한 단점을 극복하기 위해super heterodyne수신기가 발명되었습니다. AM 수신기의 블록 다이어그램은 다음 그림에 나와 있습니다.

RF 튜너 섹션
안테나가 수신 한 진폭 변조 파는 먼저 tuner circuit변압기를 통해. 튜너 회로는 LC 회로 일뿐입니다.resonant 또는 tank circuit. AM 수신기가 원하는 주파수를 선택합니다. 또한 로컬 오실레이터와 RF 필터를 동시에 조정합니다.
RF 믹서
튜너 출력의 신호는 RF-IF converter, 믹서 역할을합니다. 일정한 주파수를 생성하는 국부 발진기가 있습니다. 여기서 믹싱 프로세스는 수신 된 신호를 하나의 입력으로하고 국부 발진기 주파수를 다른 입력으로 사용합니다. 결과 출력은 믹서에 의해 생성 된 두 개의 주파수 $ \ left [\ left (f_1 + f_2 \ right), \ left (f_1-f_2 \ right) \ right] $의 혼합입니다.Intermediate Frequency (IF).
IF의 생성은 모든 반송파 주파수를 갖는 모든 스테이션 신호의 복조에 도움이됩니다. 따라서 모든 신호는 적절한 선택성을 위해 고정 반송파 주파수로 변환됩니다.
IF 필터
중간 주파수 필터는 원하는 주파수를 통과하는 대역 통과 필터입니다. 그것은 그것에 존재하는 다른 모든 원치 않는 주파수 구성 요소를 제거합니다. 이것이 IF 주파수 만 허용하는 IF 필터의 장점입니다.
AM 복조기
수신 된 AM 파는 이제 AM 복조기를 사용하여 복조됩니다. 이 복조기는 엔벨로프 감지 프로세스를 사용하여 변조 신호를 수신합니다.
오디오 증폭기
이것은 감지 된 오디오 신호를 증폭하는 데 사용되는 전력 증폭기 단계입니다. 처리 된 신호는 효과적 이도록 강화됩니다. 이 신호는 라우드 스피커로 전달되어 원래 사운드 신호를 얻습니다.
FM 수신기
FM 수신기의 블록 다이어그램은 다음 그림과 같습니다.

이 FM 수신기의 블록 다이어그램은 AM 수신기의 블록 다이어그램과 유사합니다. 두 블록의 진폭 리미터와 디엠 퍼시스 네트워크는 FM 복조기 전후에 포함됩니다. 나머지 블록의 동작은 AM 수신기의 동작과 동일합니다.
FM 변조에서 FM 파의 진폭은 일정하게 유지됩니다. 그러나 채널에 FM 파와 함께 약간의 노이즈가 추가되면 FM 파의 진폭이 달라질 수 있습니다. 따라서의 도움으로amplitude limiter 노이즈 신호의 원치 않는 피크를 제거하여 FM 파의 진폭을 일정하게 유지할 수 있습니다.
FM 송신기에서 우리는 FM 변조기 이전에 존재하는 프리 엠 퍼시스 네트워크 (고역 통과 필터)를 보았습니다. 이것은 고주파 오디오 신호의 SNR을 향상시키는 데 사용됩니다. 사전 강조의 반대 과정은 다음과 같이 알려져 있습니다.de-emphasis. 따라서이 FM 수신기에는 FM 복조기 뒤에 디엠 퍼시스 네트워크 (저역 통과 필터)가 포함됩니다. 이 신호는 전력 레벨을 높이기 위해 오디오 증폭기로 전달됩니다. 마지막으로 라우드 스피커에서 원래 사운드 신호를받습니다.
지금까지 연속파 변조에 대해 논의했습니다. 다음 장에서 펄스 변조에 대해 설명합니다. 이러한 펄스 변조 기술은 이산 신호를 처리합니다. 이제 연속 시간 신호를 이산 신호로 변환하는 방법을 살펴 보겠습니다.
연속 시간 신호를 동등한 이산 시간 신호로 변환하는 프로세스는 다음과 같이 불릴 수 있습니다. Sampling. 특정 순간의 데이터는 샘플링 프로세스에서 지속적으로 샘플링됩니다.
다음 그림은 연속 시간 신호를 보여줍니다. x(t) 및 해당 샘플링 신호 xs(t). 언제x(t) 주기적인 임펄스 트레인, 샘플링 된 신호를 곱합니다. xs(t) 획득됩니다.

ㅏ sampling signal 동일한 간격으로 샘플링 된 단위 진폭을 갖는주기적인 펄스 열입니다. $ T_s $ sampling time. 이 데이터는 $ T_s $ 순간에 전송되고 나머지 시간에 반송파 신호가 전송됩니다.
샘플링 속도
신호를 이산화하려면 샘플 간의 간격을 수정해야합니다. 그 차이를 샘플링 기간 $ T_s $라고 할 수 있습니다. 샘플링 기간의 역수는 다음과 같이 알려져 있습니다.sampling frequency 또는 sampling rate $f_s$.
수학적으로 다음과 같이 쓸 수 있습니다.
$$ f_s = \ frac {1} {T_s} $$
어디,
$ f_s $는 샘플링 주파수 또는 샘플링 속도입니다.
$ T_s $는 샘플링 기간입니다.
샘플링 정리
샘플링 속도는 메시지 신호의 데이터가 손실되거나 오버랩되지 않아야합니다. 그만큼sampling theorem "신호가 주어진 신호의 최대 주파수의 두 배 이상인 $ f_s $ 속도로 샘플링되면 신호가 정확하게 재현 될 수 있습니다. W.”
수학적으로 다음과 같이 쓸 수 있습니다.
$$ f_s \ geq 2W $$
어디,
$ f_s $는 샘플링 속도입니다.
$ W $는 주어진 신호의 가장 높은 주파수입니다.
샘플링 속도가 주어진 신호 W의 최대 주파수의 두 배와 같으면 다음과 같이 호출됩니다. Nyquist rate.
다음과 같이 불리는 샘플링 정리 Nyquist theorem, 대역폭이 제한된 함수 클래스에 대한 대역폭 측면에서 충분한 샘플 속도 이론을 제공합니다.
연속 시간 신호용 x(t)주파수 영역에서 대역 제한이있는는 다음 그림과 같이 표시됩니다.

신호가 나이 퀴 스트 속도 이상으로 샘플링되면 원래 신호를 복구 할 수 있습니다. 다음 그림은 다음보다 높은 속도로 샘플링 된 경우 신호를 설명합니다.2w 주파수 영역에서.
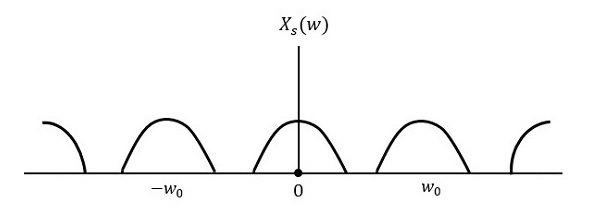
동일한 신호가 다음보다 낮은 속도로 샘플링되는 경우 2w이면 샘플링 된 신호는 다음 그림과 같습니다.

위의 패턴에서 정보가 중복되어 정보가 섞이고 손실되는 것을 알 수 있습니다. 이러한 원치 않는 겹침 현상을Aliasing.
앨리어싱은 "샘플링 된 버전의 스펙트럼에서 저주파 성분의 동일성을 취하는 신호 스펙트럼의 고주파 성분 현상"이라고 할 수 있습니다.
따라서 신호의 샘플링 속도는 나이 퀴 스트 속도로 선택됩니다. 샘플링 속도가 주어진 신호의 가장 높은 주파수의 두 배인 경우W이면 샘플링 된 신호는 다음 그림과 같습니다.

이 경우 신호는 손실없이 복구 될 수 있습니다. 따라서 이것은 좋은 샘플링 속도입니다.
연속파 변조 후 다음 분할은 펄스 변조입니다. 이 장에서는 다음과 같은 아날로그 펄스 변조 기술에 대해 설명합니다.
- 펄스 진폭 변조
- 펄스 폭 변조
- 펄스 위치 변조
펄스 진폭 변조
에 Pulse Amplitude Modulation (PAM) 기술에 따라 펄스 반송파의 진폭이 달라지며 이는 메시지 신호의 순간 진폭에 비례합니다.
펄스 진폭 변조 신호는 신호가 전체 파동의 경로를 추적하므로 원래 신호의 진폭을 따릅니다. Natural PAM에서 Nyquist 속도로 샘플링 된 신호는 효율적인 신호를 통과하여 재구성 할 수 있습니다.Low Pass Filter (LPF) 정확한 차단 주파수로.
다음 그림은 펄스 진폭 변조를 설명합니다.



PAM 신호는 LPF를 통과하지만 왜곡없이 신호를 복구 할 수 없습니다. 따라서이 노이즈를 방지하려면 플랫 탑 샘플링을 사용하십시오. 다음 그림은 플랫 탑 PAM 신호를 보여줍니다.

Flat-top sampling샘플링 된 신호를 아날로그 신호에 대해 신호의 진폭을 변경할 수없는 펄스로 표시하여 샘플링 할 수있는 프로세스입니다. 진폭의 상단은 평평하게 유지됩니다. 이 프로세스는 회로 설계를 단순화합니다.
펄스 폭 변조
에 Pulse Width Modulation (PWM) 또는 PDM (Pulse Duration Modulation) 또는 PTM (Pulse Time Modulation) 기술에 따라 펄스 반송파의 폭 또는 지속 시간 또는 시간이 달라지며 이는 메시지 신호의 순간 진폭에 비례합니다.
이 방법에서 펄스의 폭은 다양하지만 신호의 진폭은 일정하게 유지됩니다. 진폭 제한 기는 신호의 진폭을 일정하게 만드는 데 사용됩니다. 이러한 회로는 진폭을 원하는 수준으로 잘라내므로 노이즈가 제한됩니다.
다음 그림은 펄스 폭 변조 유형을 설명합니다.
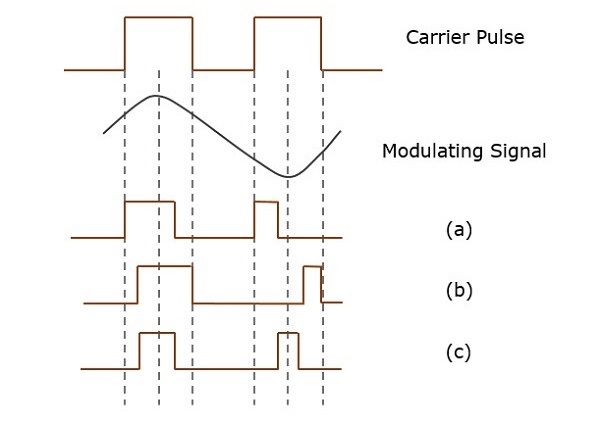
PWM에는 세 가지 유형이 있습니다.
펄스의 선행 에지는 일정하며 후행 에지는 메시지 신호에 따라 달라집니다. 이 유형의 PWM에 대한 파형은 위 그림에서 (a)로 표시됩니다.
펄스의 후행 에지는 일정하며 선행 에지는 메시지 신호에 따라 다릅니다. 이 유형의 PWM에 대한 파형은 위 그림에서 (b)로 표시됩니다.
펄스의 중심은 일정하고, 리딩 에지와 트레일 링 에지는 메시지 신호에 따라 달라집니다. 이러한 유형의 PWM에 대한 파형은 위 그림에서 (c)로 표시됩니다.
펄스 위치 변조
Pulse Position Modulation (PPM) 펄스의 진폭과 폭은 일정하게 유지되는 반면 기준 펄스의 위치를 기준으로 각 펄스의 위치는 메시지 신호의 순시 샘플링 값에 따라 달라지는 아날로그 변조 방식입니다.
송신기는 송신기와 수신기를 동기화 상태로 유지하기 위해 동기화 펄스 (또는 단순히 동기화 펄스)를 보내야합니다. 이러한 동기 펄스는 펄스의 위치를 유지하는 데 도움이됩니다. 다음 그림은 펄스 위치 변조를 설명합니다.



펄스 위치 변조는 펄스 폭 변조 신호에 따라 수행됩니다. 펄스 폭 변조 신호의 각 후행 에지는 PPM 신호에서 펄스의 시작점이됩니다. 따라서 이러한 펄스의 위치는 PWM 펄스의 폭에 비례합니다.
이점
진폭과 폭이 일정하기 때문에 처리되는 전력도 일정합니다.
불리
송신기와 수신기 사이의 동기화는 필수입니다.
PAM, PWM 및 PPM 비교
다음 표는 세 가지 변조 기술 간의 비교를 보여줍니다.
| PAM | PWM | PPM |
|---|---|---|
| 진폭이 다양합니다. | 폭이 다양하다 | 위치가 다양하다 |
| 대역폭은 펄스의 폭에 따라 다릅니다. | 대역폭은 펄스의 상승 시간에 따라 다릅니다. | 대역폭은 펄스의 상승 시간에 따라 다릅니다. |
| 순간 송신기 전력은 펄스의 진폭에 따라 다릅니다. | 순간 송신기 전력은 펄스의 진폭과 폭에 따라 다릅니다. | 순간 송신기 전력은 펄스 폭에 따라 일정하게 유지됩니다. |
| 시스템 복잡성이 높습니다. | 시스템 복잡성이 낮음 | 시스템 복잡성이 낮음 |
| 노이즈 간섭이 높습니다. | 소음 간섭이 낮음 | 소음 간섭이 낮음 |
| 진폭 변조와 유사합니다. | 주파수 변조와 유사합니다. | 위상 변조와 유사합니다. |
Transducer에너지를 한 형태에서 다른 형태로 변환하는 장치입니다. 이 장에서는 통신 시스템에 사용되는 변환기에 대해 논의하겠습니다.
트랜스 듀서가 필요한 이유는 무엇입니까?
현실 세계에서는 근처에있는 두 사람 사이의 의사 소통이 음파의 도움으로 이루어집니다. 그러나 사람이 멀리 떨어져 있으면 물리적 형태의 음파를 이용하여 정보를 손실없이 전달하기가 어렵다.
이러한 어려움을 극복하기 위해 송신기 섹션에서 변조기를 사용하고 수신기 섹션에서 복조기를 사용할 수 있습니다. 이러한 변조기와 복조기는 전기 신호로 작동합니다. 그렇기 때문에 음파를 전기 신호로 또는 그 반대로 변환해야하는 장치가 필요합니다. 이 장치를 변환기라고합니다.
다음은 변환기의 간단한 블록 다이어그램입니다.

이 변환기에는 단일 입력과 단일 출력이 있습니다. 입력에 존재하는 에너지를 다른 에너지를 갖는 동등한 출력으로 변환합니다. 기본적으로 변환기는 비전 기적 형태의 에너지를 전기적 형태로 또는 그 반대로 변환합니다.
변환기의 유형
변환기를 다음과 같이 분류 할 수 있습니다. two types 통신 시스템에서 변환기의 배치 (위치)를 기반으로합니다.
- 입력 변환기
- 출력 변환기
입력 변환기
통신 시스템의 입력에있는 변환기는 input transducer. 다음은 입력 변환기의 블록 다이어그램입니다.

이 입력 변환기는 전기가 아닌 물리량을 전기 신호로 변환합니다. 이 변환기를 사용하여 소리 나 빛과 같은 물리량을 전압이나 전류와 같은 전기량으로 변환 할 수 있습니다.Example: 마이크.
마이크는 정보 소스와 송신기 섹션 사이에있는 입력 변환기로 사용됩니다. 정보 소스는 음파의 형태로 정보를 생성합니다. 그만큼microphone진동판의 도움으로 이러한 음파를 전기 신호로 변환합니다. 이러한 전기 신호는 추가 처리에 사용될 수 있습니다.
출력 변환기
통신 시스템의 출력에있는 변환기를 출력 변환기라고합니다. 다음은 블록 다이어그램입니다.output transducer.

이 출력 변환기는 전기 신호를 전기가 아닌 물리량으로 변환합니다. 전압이나 전류와 같은 전기량은이 변환기를 사용하여 소리 나 빛과 같은 물리량으로 변환 될 수 있습니다.Example: 확성기.
시끄러운 스피커는 수신기 섹션과 대상 사이에 배치되는 출력 변환기로 사용됩니다. 수신기 섹션에있는 복조기는 복조 된 출력을 생성합니다. 그래서loud speaker전기 신호 (복조 된 출력)를 음파로 변환합니다. 따라서 라우드 스피커의 기능은 마이크의 기능과 정반대입니다.
위의 변환기 외에도 통신 시스템에 사용되는 변환기가 하나 더 있습니다. 이 변환기는 송신기 섹션의 끝에 또는 수신기 섹션의 시작에 배치 할 수 있습니다.Example: 안테나.
안테나는 전기 신호를 전자기파로 또는 그 반대로 변환하는 변환기입니다. 안테나는 다음 중 하나로 사용할 수 있습니다.transmitting antenna 또는 receiving antenna.
송신 안테나는 전기 신호를 전자기파로 변환하여 방출합니다. 한편, 수신 안테나는 수신 된 빔의 전자기파를 전기 신호로 변환합니다.
이 양방향 통신에서는 동일한 안테나를 송수신에 모두 사용할 수 있습니다.