아날로그 통신-SNR 계산
이 장에서는 수신기에서 복조되는 다양한 변조 파의 신호 대 잡음비와 성능 지수를 계산해 보겠습니다.
신호 대 잡음비
Signal-to-Noise Ratio (SNR)신호 전력 대 잡음 전력의 비율입니다. SNR 값이 높을수록 수신 된 출력의 품질이 높아집니다.
다음 공식을 사용하여 여러 지점에서 신호 대 잡음비를 계산할 수 있습니다.
Input SNR = $ \ left (SNR \ right) _I = \ frac {Average \ : \ : power \ : \ : of \ : \ : modulating \ : \ : signal} {Average \ : \ : power \ : \ : of \ : \ : 노이즈 \ : \ : at \ : \ : input} $
Output SNR = $ \ left (SNR \ right) _O = \ frac {Average \ : \ : power \ : \ : of \ : \ : demodulated \ : \ : signal} {Average \ : \ : power \ : \ : of \ : \ : 노이즈 \ : \ : at \ : \ : 출력} $
Channel SNR = $ \ left (SNR \ right) _C = \ frac {Average \ : \ : power \ : \ : of \ : \ : modulated \ : \ : signal} {Average \ : \ : power \ : \ : of \ : \ : 노이즈 \ : \ : in \ : \ : message \ : \ : bandwidth} $
공로의 그림
출력 SNR과 입력 SNR의 비율은 다음과 같이 표현할 수 있습니다. Figure of Merit. 다음과 같이 표시됩니다.F. 장치의 성능을 설명합니다.
$$ F = \ frac {\ 왼쪽 (SNR \ 오른쪽) _O} {\ 왼쪽 (SNR \ 오른쪽) _I} $$
수신기의 장점은 다음과 같습니다.
$$ F = \ frac {\ 왼쪽 (SNR \ 오른쪽) _O} {\ 왼쪽 (SNR \ 오른쪽) _C} $$
수신기의 경우 채널이 입력이기 때문입니다.
AM 시스템의 SNR 계산
노이즈 분석을 위해 AM 시스템의 다음 수신기 모델을 고려하십시오.

우리는 진폭 변조 (AM) 파가
$$ s \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) $$
$$ \ 오른쪽 화살표 s \ 왼쪽 (t \ 오른쪽) = A_c \ cos \ left (2 \ pi f_ct \ 오른쪽) + A_ck_am \ left (t \ 오른쪽) \ cos \ left (2 \ pi f_ct \ 오른쪽) $$
AM 파의 평균 전력은
$$ P_s = \ left (\ frac {A_c} {\ sqrt {2}} \ right) ^ 2 + \ left (\ frac {A_ck_am \ left (t \ right)} {\ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2}} {2} + \ frac {{A_ {c}} ^ {2} {k_ {a}} ^ {2} P} {2} $ $
$$ \ Rightarrow P_s = \ frac {{A_ {c}} ^ {2} \ left (1+ {k_ {a}} ^ {2} P \ right)} {2} $$
메시지 대역폭의 평균 잡음 전력은
$$ P_ {nc} = WN_0 $$
대체,이 값은 channel SNR 공식
$$ \ left (SNR \ right) _ {C, AM} = \ frac {Average \ : \ : Power \ : \ : of \ : \ : AM \ : \ : Wave} {Average \ : \ : Power \ : \ : / \ : \ : 노이즈 \ : \ : \ : \ : 메시지 \ : \ : 대역폭} $$
$$ \ Rightarrow \ left (SNR \ right) _ {C, AM} = \ frac {{A_ {c}} ^ {2} \ left (1+ {k_ {a}} ^ {2} \ right) P } {2WN_0} $$
어디,
P 메시지 신호의 힘 = $ \ frac {{A_ {m}} ^ {2}} {2} $
W 메시지 대역폭입니다.
위 그림과 같이 대역 통과 노이즈가 채널에서 AM 파와 혼합되었다고 가정합니다. 이 조합은 AM 복조기의 입력에 적용됩니다. 따라서 AM 복조기의 입력은 다음과 같습니다.
$$ v \ 왼쪽 (t \ 오른쪽) = s \ 왼쪽 (t \ 오른쪽) + n \ 왼쪽 (t \ 오른쪽) $$
$ \ Rightarrow v \ left (t \ right) = A_c \ left [1 + k_am \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) + $
$ \ left [n_1 \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right)-n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ right] $
$ \ Rightarrow v \ left (t \ right) = \ left [A_c + A_ck_am \ left (t \ right) + n_1 \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right)- n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) $
$ n_I \ left (t \ right) $ 및 $ n_Q \ left (t \ right) $는 잡음의 위상 및 직교 위상 성분입니다.
AM 복조기의 출력은 위 신호의 포락선에 불과합니다.
$$ d \ left (t \ right) = \ sqrt {\ left [A_c + A_cK_am \ left (t \ right) + n_I \ left (t \ right) \ right] ^ 2 + \ left (n_Q \ left (t \ 오른쪽) \ 오른쪽) ^ 2} $$
$$ \ 오른쪽 화살표 d \ 왼쪽 (t \ 오른쪽) \ 대략 A_c + A_ck_am \ 왼쪽 (t \ 오른쪽) + n_1 \ 왼쪽 (t \ 오른쪽) $$
복조 된 신호의 평균 전력은 다음과 같습니다.
$$ P_m = \ left (\ frac {A_ck_am \ left (t \ right)} {\ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2} {k_ {a} } ^ {2} P} {2} $$
출력에서 평균 잡음 전력은
$$ P_no = WN_0 $$
대체,이 값은 output SNR 공식.
$$ \ left (SNR \ right) _ {O, AM} = \ frac {Average \ : \ : Power \ : \ : of \ : \ : 복조 \ : \ : 신호} {Average \ : \ : Power \ : \ : / \ : \ : 노이즈 \ : \ : \ : \ : 출력} $$
$$ \ Rightarrow \ left (SNR \ right) _ {O, AM} = \ frac {{A_ {c}} ^ {2} {k_ {a}} ^ {2} P} {2WN_0} $$
대체, 값 Figure of merit AM 수신기 공식의.
$$ F = \ frac {\ 왼쪽 (SNR \ 오른쪽) _ {O, AM}} {\ 왼쪽 (SNR \ 오른쪽) _ {C, AM}} $$
$$ \ Rightarrow F = \ left (\ frac {{A_ {c} ^ {2}} {k_ {a} ^ {2}} P} {2WN_0} \ right) / \ left (\ frac {{A_ { c}} ^ {2} \ left (1+ {k_ {a}} ^ {2} \ right) P} {2WN_0} \ right) $$
$$ \ Rightarrow F = \ frac {{K_ {a}} ^ {2} P} {1+ {K_ {a}} ^ {2} P} $$
따라서 AM 수신기의 성능 지수는 1 미만입니다.
DSBSC 시스템의 SNR 계산
잡음을 분석하기 위해 DSBSC 시스템의 다음 수신기 모델을 고려하십시오.

우리는 DSBSC 변조 파가
$$ s \ left (t \ right) = A_cm \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) $$
DSBSC 변조 파의 평균 전력은 다음과 같습니다.
$$ P_s = \ left (\ frac {A_cm \ left (t \ right)} {\ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2} P} {2} $$
메시지 대역폭의 평균 잡음 전력은
$$ P_ {nc} = WN_0 $$
대체,이 값은 channel SNR 공식.
$$ \ left (SNR \ right) _ {C, DSBSC} = \ frac {Average \ : \ : Power \ : \ : of \ : \ : DSBSC \ : \ : modulated \ : \ : wave} {Average \ : \ : 전원 \ : \ : of \ : \ : 노이즈 \ : \ : in \ : \ : 메시지 \ : \ : 대역폭} $$
$$ \ Rightarrow \ left (SNR \ right) _ {C, DSBSC} = \ frac {{A_ {c}} ^ {2} P} {2WN_0} $$
위 그림과 같이 대역 통과 잡음이 채널에서 DSBSC 변조 파와 혼합되었다고 가정합니다. 이 조합은 제품 변조기에 대한 입력 중 하나로 적용됩니다. 따라서이 제품 변조기의 입력은
$$ v_1 \ 왼쪽 (t \ 오른쪽) = s \ 왼쪽 (t \ 오른쪽) + n \ 왼쪽 (t \ 오른쪽) $$
$$ \ Rightarrow v_1 \ left (t \ right) = A_cm \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) + \ left [n_I \ left (t \ right) \ cos \ left ( 2 \ pi f_ct \ right)-n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ right] $$
$$ \ Rightarrow v_1 \ left (t \ right) = \ left [A_cm \ left (t \ right) + n_I \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) $$
로컬 오실레이터는 캐리어 신호 $ c \ left (t \ right) = \ cos \ left (2 \ pi f_ct \ right) $를 생성합니다. 이 신호는 제품 변조기에 대한 또 다른 입력으로 적용됩니다. 따라서 제품 변조기는 $ v_1 \ left (t \ right) $ 및 $ c \ left (t \ right) $의 곱인 출력을 생성합니다.
$$ v_2 \ 왼쪽 (t \ 오른쪽) = v_1 \ 왼쪽 (t \ 오른쪽) c \ 왼쪽 (t \ 오른쪽) $$
위 방정식에서 $ v_1 \ left (t \ right) $ 및 $ c \ left (t \ right) $ 값을 대체하십시오.
$$ \ Rightarrow v_2 \ left (t \ right) = \ left (\ left [A_cm \ left (t \ right) + n_I \ left (t \ right) \ right] \ cos \ left (2 \ pi f_ct \ right )-n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ right) \ cos \ left (2 \ pi f_ct \ right) $$
$$ \ Rightarrow v_2 \ left (t \ right) = \ left [A_c m \ left (t \ right) + n_I \ left (t \ right) \ right] \ cos ^ 2 \ left (2 \ pi f_ct \ right ) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ cos \ left (2 \ pi f_ct \ right) $$
$$ \ Rightarrow v_2 \ left (t \ right) = \ left [A_c m \ left (t \ right) + n_I \ left (t \ right) \ right] \ left (\ frac {1+ \ cos \ left ( 4 \ pi f_ct \ right)} {2} \ right) -n_Q \ left (t \ right) \ frac {\ sin \ left (4 \ pi f_ct \ right)} {2} $$
위의 신호가 로우 패스 필터의 입력으로 적용되면 로우 패스 필터의 출력을 다음과 같이 얻을 수 있습니다.
$$ d \ left (t \ right) = \ frac {\ left [A_c m \ left (t \ right) + n_I \ left (t \ right) \ right]} {2} $$
복조 된 신호의 평균 전력은 다음과 같습니다.
$$ P_m = \ left (\ frac {A_cm \ left (t \ right)} {2 \ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2} P} {8 } $$
출력에서 평균 잡음 전력은
$$ P_ {no} = \ frac {WN_0} {4} $$
대체,이 값은 output SNR 공식.
$$ \ left (SNR \ right) _ {O, DSBSC} = \ frac {Average \ : \ : Power \ : \ : of \ : \ : 복조 \ : \ : 신호} {Average \ : \ : Power \ : \ : / \ : \ : 노이즈 \ : \ : \ : \ : 출력} $$
$$ \ Rightarrow \ left (SNR \ right) _ {O, DSBSC} = \ left (\ frac {{A_ {c}} ^ {2} P} {8} \ right) / \ left (\ frac {WN_0 } {4} \ right) = \ frac {{A_ {c}} ^ {2} P} {2WN_0} $$
대체, 값 Figure of merit DSBSC 수신기 공식의.
$$ F = \ frac {\ 왼쪽 (SNR \ 오른쪽) _ {O, DSBSC}} {\ 왼쪽 (SNR \ 오른쪽) _ {C, DSBSC}} $$
$$ \ 오른쪽 화살표 F = \ left (\ frac {{A_ {c}} ^ {2} P} {2WN_0} \ right) / \ left (\ frac {{A_ {c}} ^ {2} P} { 2WN_0} \ 오른쪽) $$
$$ \ 오른쪽 화살표 F = 1 $$
따라서 DSBSC 수신기의 성능 지수는 1입니다.
SSBSC 시스템의 SNR 계산
잡음을 분석하기 위해 SSBSC 시스템의 다음 수신기 모델을 고려하십시오.
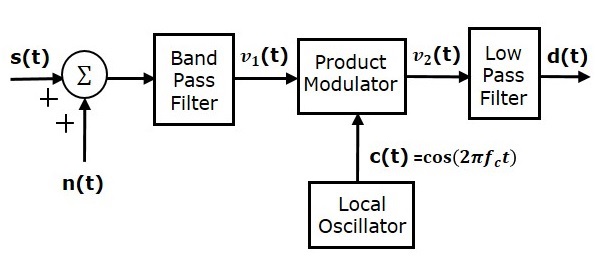
우리는 더 낮은 측 파대를 갖는 SSBSC 변조 파가
$$ s \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] $$
SSBSC 변조 파의 평균 전력은 다음과 같습니다.
$$ P_s = \ left (\ frac {A_mA_c} {2 \ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8} $$
메시지 대역폭의 평균 잡음 전력은
$$ P_ {nc} = WN_0 $$
대체,이 값은 channel SNR 공식.
$$ \ left (SNR \ right) _ {C, SSBSC} = \ frac {Average \ : \ : Power \ : \ : of \ : \ : SSBSC \ : \ : modulated \ : \ : wave} {Average \ : \ : 전원 \ : \ : of \ : \ : 노이즈 \ : \ : in \ : \ : 메시지 \ : \ : 대역폭} $$
$$ \ Rightarrow \ left (SNR \ right) _ {C, SSBSC} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} $$
위 그림과 같이 대역 통과 잡음이 채널에서 SSBSC 변조 파와 혼합되었다고 가정합니다. 이 조합은 제품 변조기에 대한 입력 중 하나로 적용됩니다. 따라서이 제품 변조기의 입력은
$$ v_1 \ 왼쪽 (t \ 오른쪽) = s \ 왼쪽 (t \ 오른쪽) + n \ 왼쪽 (t \ 오른쪽) $$
$$ v_1 \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] + n_I \ left (t \ right) \ cos \ left (2 \ pi f_ct \ right) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) $$
국부 발진기는 반송파 신호 $ c \ left (t \ right) = \ cos \ left (2 \ pi f_ct \ right) $를 생성합니다. 이 신호는 제품 변조기에 대한 또 다른 입력으로 적용됩니다. 따라서 제품 변조기는 $ v_1 \ left (t \ right) $ 및 $ c \ left (t \ right) $의 곱인 출력을 생성합니다.
$$ v_2 \ 왼쪽 (t \ 오른쪽) = v_1 \ 왼쪽 (t \ 오른쪽) c \ 왼쪽 (t \ 오른쪽) $$
위 방정식에서 $ v_1 \ left (t \ right) $ 및 $ c \ left (t \ right) $ 값을 대입합니다.
$ \ Rightarrow v_2 (t) = (\ frac {A_mA_c} {2} \ cos [2 \ pi (f_c-f_m) t] + n_I (t) \ cos (2 \ pi f_ct)-$
$ n_Q (t) \ sin (2 \ pi f_ct)) \ cos (2 \ pi f_ct) $
$ \ Rightarrow v_2 \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left (f_c-f_m \ right) t \ right] \ cos \ left (2 \ pi f_ct \ 오른쪽) + $
$ n_I \ left (t \ right) \ cos ^ 2 \ left (2 \ pi f_ct \ right) -n_Q \ left (t \ right) \ sin \ left (2 \ pi f_ct \ right) \ cos \ left (2 \ pi f_ct \ 오른쪽) $
$ \ Rightarrow v_2 \ left (t \ right) = \ frac {A_mA_c} {4} \ left \ {\ cos \ left [2 \ pi \ left (2f_c-f_m \ right) t \ right] + \ cos \ left (2 \ pi f_mt \ right) \ right \} + $
$ n_I \ left (t \ right) \ left (\ frac {1+ \ cos \ left (4 \ pi f_ct \ right)} {2} \ right)-n_Q \ left (t \ right) \ frac {\ sin \ 왼쪽 (4 \ pi f_ct \ 오른쪽)} {2} $
위의 신호가 로우 패스 필터의 입력으로 적용되면 로우 패스 필터의 출력을 다음과 같이 얻을 수 있습니다.
$$ d \ left (t \ right) = \ frac {A_mA_c} {2} \ cos \ left (2 \ pi f_mt \ right) + \ frac {n_I \ left (t \ right)} {2} $$
복조 된 신호의 평균 전력은 다음과 같습니다.
$$ P_m = \ left (\ frac {A_mA_c} {4 \ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {32} $$
출력에서 평균 잡음 전력은
$$ P_ {no} = \ frac {WN_0} {4} $$
대체,이 값은 output SNR 공식
$$ \ left (SNR \ right) _ {O, SSBSC} = \ frac {Average \ : \ : Power \ : \ : of \ : \ : 복조 \ : \ : signal} {Average \ : \ : Power \ : \ : / \ : \ : 노이즈 \ : \ : \ : \ : 출력} $$
$$ \ Rightarrow \ left (SNR \ right) _ {O, SSBSC} = \ left (\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {32} \ right ) / \ left (\ frac {WN_0} {4} \ right) = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} $$
대체, 값 Figure of merit SSBSC 수신기 공식
$$ F = \ frac {\ 왼쪽 (SNR \ 오른쪽) _ {O, SSBSC}} {\ 왼쪽 (SNR \ 오른쪽) _ {C, SSBSC}} $$
$$ F = \ left (\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} \ right) / \ left (\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} \ right) $$
$$ F = 1 $$
따라서 SSBSC 수신기의 성능 지수는 1입니다.