우주론-각 지름 거리
이 장에서는 각도 지름 거리가 무엇이며 우주론에서 어떻게 도움이되는지 이해합니다.
현재 우주를 위해-
$ \ Omega_ {m, 0} \ : = \ : 0.3 $
$ \ Omega _ {\ wedge, 0} \ : = \ : 0.69 $
$ \ Omega_ {rad, 0} \ : = \ : 0.01 $
$ \ Omega_ {k, 0} \ : = \ : 0 $
우리는 지금까지 두 가지 유형의 거리를 연구했습니다.
Proper distance (lp) − 광자가 소스에서 우리까지 이동하는 거리, 즉 Instantaneous distance.
Comoving distance (lc) − 확장되지 않는 공간에서 물체 사이의 거리, 즉, distance in a comoving frame of reference.
적색 편이에 따른 거리
시간에 광자를 방출하는 은하를 생각해보십시오. t1 관찰자에 의해 감지되는 t0. 우리는 은하까지의 적절한 거리를 다음과 같이 쓸 수 있습니다.
$$ l_p = \ int_ {t_1} ^ {t_0} cdt $$
은하계의 적색 편이를 z,
$$ \ Rightarrow \ frac {\ mathrm {d} z} {\ mathrm {d} t} =-\ frac {1} {a ^ 2} \ frac {\ mathrm {d} a} {\ mathrm {d} t} $$
$$ \ Rightarrow \ frac {\ mathrm {d} z} {\ mathrm {d} t} =-\ frac {\ frac {\ mathrm {d} a} {\ mathrm {d} t}} {a} \ frac {1} {a} $$
$$ \ 따라서 \ frac {\ mathrm {d} z} {\ mathrm {d} t} =-\ frac {H (z)} {a} $$
이제 언제든지 은하계의 이동 거리 t 될 것입니다-
$$ l_c = \ frac {l_p} {a (t)} $$
$$ l_c = \ int_ {t_1} ^ {t_0} \ frac {cdt} {a (t)} $$
z 측면에서
$$ l_c = \ int_ {t_0} ^ {t_1} \ frac {cdz} {H (z)} $$
다음과 같이 거리를 찾는 두 가지 방법이 있습니다.
Flux-Luminosity 관계
$$ F = \ frac {L} {4 \ pi d ^ 2} $$
어디 d 소스에서의 거리입니다.
소스의 각도 지름 거리
소스의 크기를 알면 각도 너비가 관찰자로부터의 거리를 알려줍니다.
$$ \ theta = \ frac {D} {l} $$
어디 l 소스의 각 직경 거리입니다.
θ 소스의 각도 크기입니다.
D 소스의 크기입니다.
크기 D와 각 크기의 은하를 고려하십시오. dθ.
우리는 알고 있습니다.
$$ d \ theta = \ frac {D} {d_A} $$
$$ \ 따라서 D ^ 2 = a (t) ^ 2 (r ^ 2 d \ theta ^ 2) \ quad \ because dr ^ 2 = 0; \ : 디 \ 파이 ^ 2 \ 약 0 $$
$$ \ 오른쪽 화살표 D = a (t) rd \ theta $$
바꾸다 r ...에 rc, 은하의 이동 거리, 우리는-
$$ d \ theta = \ frac {D} {r_ca (t)} $$
여기에서 우리가 선택한다면 t = t0, 우리는 은하계까지의 현재 거리를 측정하게됩니다. 그러나D광자가 방출 될 때 측정됩니다. 따라서t = t0, 우리는 은하까지 더 먼 거리를 가지므로 그 크기를 과소 평가합니다. 따라서 우리는 시간을 사용해야합니다t1.
$$ \ 따라서 d \ theta = \ frac {D} {r_ca (t_1)} $$
이것을 이전 결과와 비교하면 다음과 같습니다.
$$ d_ \ wedge = a (t_1) r_c $$
$$ r_c = l_c = \ frac {d_ \ wedge} {a (t_1)} = d_ \ wedge (1 + z_1) \ quad \ because 1 + z_1 = \ frac {1} {a (t_1)} $$
따라서,
$$ d_ \ wedge = \ frac {c} {1 + z_1} \ int_ {0} ^ {z_1} \ frac {dz} {H (z)} $$
dA 객체의 각도 지름 거리입니다.
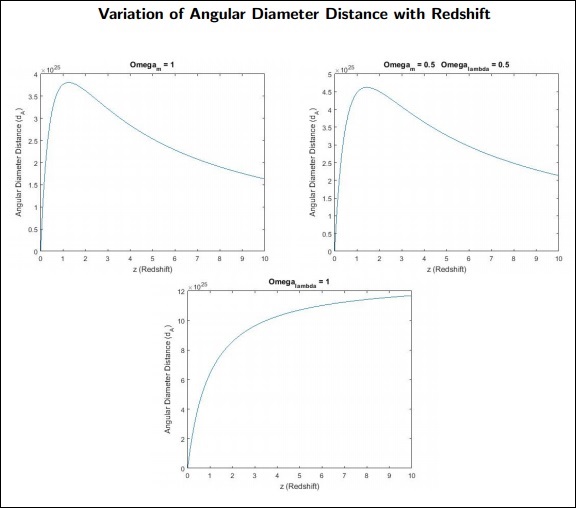
기억해야 할 사항
소스의 크기를 알면 각도 너비가 관찰자로부터의 거리를 알려줍니다.
적절한 거리는 광자가 소스에서 우리까지 이동하는 거리입니다.
Comoving distance는 확장되지 않는 공간에서 물체 사이의 거리입니다.