우주론-Robertson-Walker Metric
이 장에서는 Robertson-Walker Metric에 대해 자세히 이해합니다.
시간에 따른 스케일 팩터 변화 모델
먼 은하에서 광자가 방출된다고 가정합니다. 공간은 모든 방향에서 광자를 위해 앞으로 있습니다. 우주의 팽창은 모든 방향에 있습니다. 다음 단계에서 스케일 팩터가 시간에 따라 어떻게 변하는 지 살펴 보겠습니다.
Step 1 − 정적 우주의 경우 축척 계수는 1입니다. 즉, comoving 거리의 값은 개체 사이의 거리입니다.
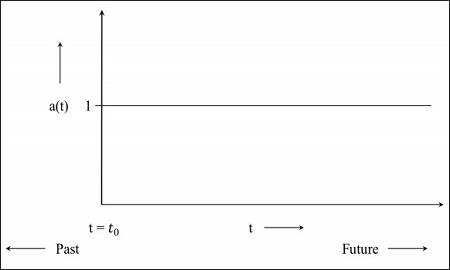
Step 2− 다음 이미지는 계속 확장되고 있지만 속도가 감소하는 우주의 그래프입니다. 이는 그래프가 과거에 시작된다는 것을 의미합니다. 그만큼t = 0 우주가 그 지점에서 시작되었음을 나타냅니다.

Step 3 − 다음 이미지는 빠른 속도로 팽창하는 우주의 그래프입니다.

Step 4 − 다음 이미지는 지금부터 수축을 시작하는 우주의 그래프입니다.

축척 계수의 값이 0 우주가 수축하는 동안 물체 사이의 거리가 0즉, 적절한 거리는 0. 현재 우주에서 물체 사이의 거리 인 comoving distance는 일정한 양입니다. 향후 스케일 팩터가0, 모든 것이 더 가까워 질 것입니다. 모델은 유니버스의 구성 요소에 따라 다릅니다.
평면 (유클리드 : 곡률에 대한 매개 변수 없음) 확장 우주에 대한 메트릭은 다음과 같이 주어집니다.
$$ ds ^ 2 = a ^ 2 (t) \ left (dr ^ 2 + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2 \ right) $$
시공간의 경우, 위 방정식에서 얻은 선 요소는 다음과 같이 수정됩니다.
$$ ds ^ 2 = c ^ 2dt ^ 2-\ left \ {a ^ 2 (t) \ left (dr ^ 2 + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2 \ 오른쪽) \ right \} $$
공간 – 시간의 경우 광자가 방출되는 시간과 감지되는 시간이 다릅니다. 적절한 거리는 우주의 팽창으로 인해 시간이 지남에 따라 변할 수있는 물체까지의 순간적인 거리입니다. 광자가 우리에게 도달하기 위해 다른 물체에서 이동 한 거리입니다. comoving 거리와 관련이 있습니다.
$$ d_p = a (t) \ times d_c $$
여기서 $ d_p $는 적절한 거리이고 $ d_c $는 고정 된 comoving 거리입니다.
현재 우주에서 물체까지 측정 된 거리는 comoving distance로 간주되며 이는 comoving distance가 고정되고 확장에 의해 변하지 않음을 의미합니다. 과거에는 축척 계수가 1보다 작았으며 이는 적절한 거리가 더 작다는 것을 나타냅니다.
은하로의 적색 편이를 측정 할 수 있습니다. 따라서 적절한 거리 $ d_p $는 $ c \ times t (z) $에 해당합니다. 여기서 $ t (z) $는 적색 편이를 향한 룩백 시간이고 c는 진공 상태에서 빛의 속도입니다. 룩백 시간은 redshift의 함수입니다.(z).
위의 개념을 바탕으로 $ d_p = a (t) \ times d_c $ 시나리오에서 우주적 적색 편이가 어떻게 해석되는지 분석해 보겠습니다.
광자 (지구 경계)가 은하 G에서 방출된다고 가정합니다. $ t_ {em} $는 광자가 방출 된 시간에 해당합니다. $ a (t_ {em}) $는 광자가 방출 될 당시의 축척 비율이었습니다. 광자가 감지 될 때까지 우주 전체가 확장되었습니다. 즉, 감지시 광자가 적색 편이됩니다. $ t_ {obs} $는 광자가 감지 된 시간에 해당하고 해당 배율 인수는 $ a (t_ {obs}) $입니다.
우주가 성장한 요인은 다음과 같습니다.
$$ \ frac {a (t_ {obs})} {a (t_ {em})} $$
파장이 확장 된 요인은-
$$ \ frac {\ lambda_ {obs}} {\ lambda_ {em}} $$
이것은 우주가 성장한 요인과 같습니다. 기호에는 일반적인 의미가 있습니다. 따라서,
$$ \ frac {a (t_ {obs})} {a (t_ {em})} = \ frac {\ lambda_ {obs}} {\ lambda_ {em}} $$
우리는 redshift (z) -
$$ z = \ frac {\ lambda_ {obs}-\ lambda_ {em}} {\ lambda_ {em}} = \ frac {\ lambda_ {obs}} {\ lambda_ {em}}-1 $$
$$ 1 + z = \ frac {a (t_ {obs})} {a (t_ {em})} $$
스케일 팩터의 현재 값은 1이므로 $ a (t_ {obs}) = 1 $이며 과거에 $ a (t) $에 의해 광자가 방출되었을 때 스케일 팩터를 나타냅니다.
따라서,
$$ 1 + z = \ frac {1} {a (t)} $$
우주론에서 적색 편이의 해석
이를 이해하기 위해 다음 예제를 살펴 보겠습니다. If $ z = 2 $ then $ a (t) = 1 / 3 $.
그것은 빛이 그 물체를 떠난 이후 우주가 3 배나 확장되었음을 의미합니다. 공간이 방출 물체에서 이동하는 동안 동일한 요소만큼 확장 되었기 때문에 수신 된 방사선의 파장이 3 배 확장되었습니다. 이러한 큰 값에서z, 적색 편이는 주로 우주적 적색 편이이며 우리에 대한 물체의 실제 후퇴 속도에 대한 유효한 척도가 아닙니다.
우주 마이크로파 배경 (CMB)의 경우 z = 1089, 즉 현재 우주가 ∼1090. 편평한 유클리드 확장 우주에 대한 메트릭은 다음과 같이 제공됩니다.
$$ ds ^ 2 = a ^ 2 (t) (dr ^ 2 + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2) $$
모든 곡률로 메트릭을 작성하고 싶습니다.
Robertson and Walker 모든 곡률 우주 (균질 및 등방성)에 대해 입증 된 메트릭은 다음과 같이 제공됩니다.
$$ ds ^ 2 = a ^ 2 (t) \ left [\ frac {dr ^ 2} {1-kr ^ 2} + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2 \ 오른쪽] $$
이것은 일반적으로 Robertson–Walker Metric공간의 모든 토폴로지에 적용됩니다. $ dr ^ 2 $의 추가 요소에 유의하십시오. 여기 곡률 상수입니다.
우주의 기하학
우주의 기하학은 다음과 같은 곡률의 도움으로 설명됩니다.
- 양의 곡률
- 음의 곡률
- 제로 곡률
이들 각각을 자세히 이해합시다.
양의 곡률
곡률 표면의 어느 지점에서든 그려진 접선 평면이 표면의 어떤 지점에서도 교차하지 않는 경우이를 양의 곡률을 가진 표면이라고합니다. 즉, 표면은 해당 지점에서 접하는 평면의 한면에 머물러 있습니다. 구의 표면에는 양의 곡률이 있습니다.
음의 곡률
곡률 표면의 한 지점에 그려진 접평면이 곡면의 임의 지점에서 교차하는 경우이를 음의 곡률을 갖는 표면이라고합니다. 즉, 표면이 접평면에서 서로 다른 두 방향으로 구부러집니다. 안장 모양의 표면에는 음의 곡률이 있습니다.
이제 구의 표면을 고려하십시오. 삼각형은 측지 (큰 원의 호)과 3 점에 가입하여 구체의 표면에 구성되어있는 경우, 구형 삼각형의 내각의 합보다 큰 180 o를 예 -
$$ \ 알파 + \ 베타 + \ 감마> \ pi $$
이러한 공간을 양의 곡선 공간이라고합니다. 또한 곡률은 균일하고 등방성입니다. 일반적으로 구형 삼각형의 꼭지점 각도는 다음 관계식을 따릅니다.
$$ \ alpha + \ beta + \ gamma = \ pi + A / R ^ 2 $$
어디 A 삼각형의 면적이고 R구의 반경입니다. 다음 이미지는 양의 곡선 공간을 보여줍니다.

양의 곡률의 경우 평행선이 만나야합니다. 긍정적으로 구부러진 공간 인 지구 표면을 고려하십시오. 적도에서 두 개의 시작점을 선택하십시오. 적도를 직각으로 교차하는 선을 경도선이라고합니다. 이러한 선은 적도를 직각으로 교차하므로 평행선이라고 할 수 있습니다. 적도에서 시작하여 결국 극점에서 교차합니다. 이 방법은Carl Gauss 그리고 다른 사람들은 지구의 토폴로지를 이해합니다.
음으로 고려 곡선 - 공간 (아래 그림과 안장) 내부의 합이 삼각형의 각도를 180도 이하이다 O 즉, -
$$ \ 알파 + \ 베타 + \ 감마 <\ pi $$
정점에서의 각도는 관계식을 따릅니다.
$$ \ alpha + \ beta + \ gamma = \ pi-A / R ^ 2 $$

제로 곡률
평면 표면에는 곡률이 없습니다. 이제 평평한 공간의 경우 평면을 취하고 3 개의 점을 측지선 (직선)과 결합하여 삼각형을 구성하면 각도의 내부 합은 다음과 같습니다.
$$ \ alpha + \ beta + \ gamma = \ pi $$
다음 이미지는 평평한 2 차원 공간입니다.

공간이 균일하고 등방성을 갖기를 원하면 공간이 균일하게 평평 할 수 있거나 균일 한 양의 곡률을 가질 수 있거나 균일 한 음의 곡률을 가질 수있는 세 가지 가능성 만 남습니다.
곡률 상수는 다음 세 가지 값 중 하나를 가정 할 수 있습니다.
$$ k = \ begin {cases} +1, & for \ : a \ : 양수 \ : 곡선 \ : space; \\\ quad 0, & for \ : a \ : 평평한 \ : space; \\-1, & for \ : a \ : 음수 \ : 곡선 \ : 공백; \ end {cases} $$
우주의 글로벌 토폴로지
우주에는 특정 토폴로지가 있지만 로컬에는 주름이있을 수 있습니다. 물질이 공간에 어떻게 분포되어 있는지에 따라 곡률에 더 작은 변화가 있습니다. 우주 어디에 있든 동일한 실제 크기를 가진 객체 클래스가 있다고 가정 해 보겠습니다. 즉, 표준 양초와 같습니다. 밝기는 같지 않지만 크기는 같습니다.
물체가 양의 곡선 공간에 있고 광자가 점 A (물체의 한쪽 끝)와 B (물체의 다른 쪽 끝)에서 오는 경우 광자는 측지선 경로를 통해 양의 곡선 공간에서 평행하게 전파되고 결국 만나게됩니다. . C의 관찰자에게는 서로 다른 방향의 두 지점에서 나온 것처럼 보입니다.
물체가 지역 우주에 있고 각도 크기를 측정하면 곡률의 영향을받지 않습니다. 더 큰 적색 편이에서 동일한 클래스의 객체가 보이면 각도 크기는 상관 관계가 없습니다.
$$ \ theta = \ frac {d} {r} $$
어디 d 개체의 크기이고 r는 물체까지의 거리입니다. 즉, 크기가 로컬 크기보다 크면 곡률이 양수임을 의미합니다. 다음 이미지는 양의 곡선 공간에서 감지 된 광자를 표현한 것입니다.

표준 크기와 형태를 가진 실제 천체 물리학 적 물체는 없다는 점에 유의해야합니다. 비록 거대한 타원 cD- 은하는 표준 양초에 맞는 것으로 생각되었지만 시간이 지남에 따라 진화하는 것으로 밝혀졌습니다.
은하까지의 거리 찾기
이 섹션에서는 다음 이미지를 고려하여 은하까지의 거리를 찾는 방법에 대해 설명합니다.

우주 휴식 프레임의 (r, θ,)에있는 은하수를 고려하십시오. 하나는 0을 취할 수 있습니다. (0, θ, ϕ), 즉 동질성 가정을 호출하여 우주의 중심.
(r1, θ,)에있는 은하 'G'를 생각해보십시오. 거리 (적절)는 광자가 이동하는 가장 짧은 방사형 거리입니다. 공간-시간의 대칭에서 r = 0에서 r = r1까지의 널 측지선은 공간에서 일정한 방향을 갖습니다. 방사형 전파에서 각도 좌표는 변경되지 않습니다. 각도 좌표가 변경되면 최단 경로가 아닙니다. 이것이 dr 2 에 곡률 항이 존재하는 이유 입니다.
기억해야 할 사항
우주의 팽창은 모든 방향에 있습니다.
우주는 스케일 팩터의 진화에 따라 정적이고 확장되거나 축소 될 수 있습니다.
cD 은하는 시간이 지남에 따라 진화하므로 표준 양초로 사용할 수 없습니다.
우주에는 특정 토폴로지가 있지만 로컬에는 주름이있을 수 있습니다.