Teoria rezonansu adaptacyjnego
Sieć ta została stworzona przez Stephena Grossberga i Gail Carpenter w 1987 roku. Opiera się na konkurencji i wykorzystuje model uczenia się bez nadzoru. Sieci Adaptive Resonance Theory (ART), jak sama nazwa wskazuje, są zawsze otwarte na nowe uczenie się (adaptacyjne) bez utraty starych wzorców (rezonans). Zasadniczo sieć ART jest klasyfikatorem wektorów, który akceptuje wektor wejściowy i klasyfikuje go do jednej z kategorii w zależności od tego, który z przechowywanych wzorców najbardziej przypomina.
Dyrektor operacyjny
Główną operację klasyfikacji ART można podzielić na następujące fazy -
Recognition phase- Wektor wejściowy jest porównywany z klasyfikacją przedstawioną w każdym węźle warstwy wyjściowej. Sygnał wyjściowy neuronu przyjmuje wartość „1”, jeśli najlepiej pasuje do zastosowanej klasyfikacji, w przeciwnym razie przyjmuje wartość „0”.
Comparison phase- W tej fazie wykonywane jest porównanie wektora wejściowego z wektorem warstwy porównawczej. Warunkiem zresetowania jest, aby stopień podobieństwa był mniejszy niż parametr czujności.
Search phase- W tej fazie sieć wyszuka reset, a także dopasowanie wykonane w powyższych fazach. Stąd, jeśli nie byłoby resetu i mecz jest całkiem dobry, to klasyfikacja się kończy. W przeciwnym razie proces zostałby powtórzony, a inny zapisany wzorzec musiałby zostać wysłany, aby znaleźć prawidłowe dopasowanie.
ART1
Jest to rodzaj ART, który jest przeznaczony do grupowania wektorów binarnych. Możemy to zrozumieć dzięki jego architekturze.
Architektura ART1
Składa się z następujących dwóch jednostek -
Computational Unit - Składa się z następujących -
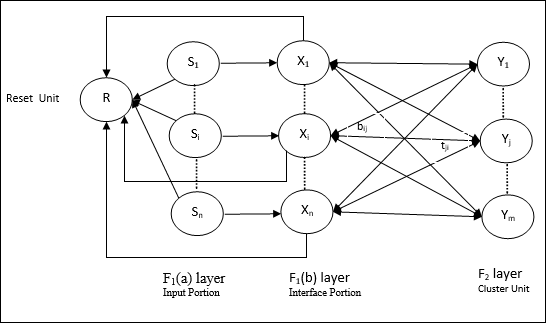
Input unit (F1 layer) - Ponadto ma następujące dwie porcje -
F1(a) layer (Input portion)- W ART1 nie byłoby przetwarzania w tej części, zamiast mieć tylko wektory wejściowe. Jest on połączony z F 1 (B), warstwa (część Interface).
F1(b) layer (Interface portion)- Ta część łączy sygnał z części wejściowej z sygnałem warstwy F 2 . Warstwa F 1 (b) jest połączona z warstwą F 2 ciężarkami od dołu do górybiji F 2 warstwa jest połączona F 1 (b) z góry na dół warstwy wagtji.
Cluster Unit (F2 layer)- To jest warstwa konkurencyjna. Do nauki wzorca wejściowego wybierana jest jednostka o największej wartości wejściowej netto. Aktywacja wszystkich innych jednostek klastra jest ustawiona na 0.
Reset Mechanism- Działanie tego mechanizmu opiera się na podobieństwie między wagą odgórną a wektorem wejściowym. Otóż, jeśli stopień tego podobieństwa jest mniejszy niż parametr czujności, wówczas klaster nie może nauczyć się wzorca i nastąpi odpoczynek.
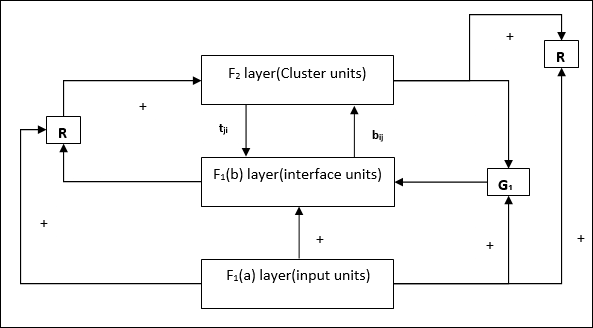
Supplement Unit - Właściwie problem z mechanizmem resetowania polega na tym, że warstwa F2muszą być hamowane pod pewnymi warunkami i muszą być również dostępne, gdy ma miejsce nauka. Dlatego dwie dodatkowe jednostki, a mianowicie:G1 i G2 jest dodawany wraz z resetem jednostki, R. Nazywają sięgain control units. Jednostki te odbierają i wysyłają sygnały do innych jednostek obecnych w sieci.‘+’ wskazuje sygnał pobudzający, podczas gdy ‘−’ wskazuje na sygnał hamujący.
Używane parametry
Używane są następujące parametry -
n - Liczba elementów w wektorze wejściowym
m - Maksymalna liczba klastrów, które można utworzyć
bij- Waga od warstwy F 1 (b) do F 2 , tj. Wagi oddolne
tji- Waga od warstwy F 2 do F 1 (b), czyli ciężary odgórne
ρ - parametr czujności
||x|| - Norma wektora x
Algorytm
Step 1 - Zainicjuj szybkość uczenia się, parametr czujności i wagi w następujący sposób -
$$ \ alpha \:> \: 1 \: \: i \: \: 0 \: <\ rho \: \ leq \: 1 $$
$$ 0 \: <\: b_ {ij} (0) \: <\: \ frac {\ alpha} {\ alpha \: - \: 1 \: + \: n} \: \: i \: \: t_ {ij} (0) \: = \: 1 $$
Step 2 - Kontynuuj krok 3-9, jeśli warunek zatrzymania nie jest spełniony.
Step 3 - Kontynuuj krok 4-6 dla każdego wejścia treningowego.
Step 4- Ustaw aktywacje wszystkich jednostek F 1 (a) i F 1 w następujący sposób
F2 = 0 and F1(a) = input vectors
Step 5- Sygnał wejściowy z warstwy F 1 (a) do F 1 (b) musi być przesłany jak
$$ s_ {i} \: = \: x_ {i} $$
Step 6- Dla każdego zablokowanego węzła F 2
$ y_ {j} \: = \: \ sum_i b_ {ij} x_ {i} $ warunkiem jest yj ≠ -1
Step 7 - Wykonaj kroki 8-10, gdy reset jest prawdziwy.
Step 8 - Znajdź J dla yJ ≥ yj dla wszystkich węzłów j
Step 9- Ponownie obliczyć aktywację na F 1 (b) w następujący sposób
$$ x_ {i} \: = \: sitJi $$
Step 10 - Teraz, po obliczeniu normy wektora x i wektor smusimy sprawdzić stan resetowania w następujący sposób -
Jeśli ||x||/ ||s|| <parametr czujności ρ, Theninhibit node J i przejdź do kroku 7
Inaczej, jeśli ||x||/ ||s|| ≥ parametr czujności ρ, a następnie przejdź dalej.
Step 11 - Aktualizacja wagi dla węzła J można zrobić w następujący sposób -
$$ b_ {ij} (nowy) \: = \: \ frac {\ alpha x_ {i}} {\ alpha \: - \: 1 \: + \: || x ||} $$
$$ t_ {ij} (nowy) \: = \: x_ {i} $$
Step 12 - Warunek zatrzymania algorytmu musi zostać sprawdzony i może wyglądać następująco -
- Nie mają żadnej zmiany wagi.
- Reset nie jest wykonywany dla jednostek.
- Osiągnięto maksymalną liczbę epok.