Uczenie się bez nadzoru
Jak sama nazwa wskazuje, ten rodzaj nauki odbywa się bez nadzoru nauczyciela. Ten proces uczenia się jest niezależny. Podczas uczenia SSN w ramach uczenia się bez nadzoru wektory wejściowe podobnego typu są łączone w klastry. Po zastosowaniu nowego wzorca wejściowego sieć neuronowa daje odpowiedź wyjściową wskazującą klasę, do której należy wzorzec wejściowy. W tym przypadku nie byłoby informacji zwrotnej ze środowiska, który powinien być pożądany i czy jest poprawny, czy nieprawidłowy. Stąd w tego typu uczeniu się sama sieć musi odkryć wzorce, cechy z danych wejściowych i relację danych wejściowych do danych wyjściowych.
Zwycięzca bierze wszystkie sieci
Tego rodzaju sieci opierają się na zasadzie konkurencyjnego uczenia się i wykorzystują strategię, w której jako zwycięzca wybiera neuron o największych łącznych nakładach. Połączenia między neuronami wyjściowymi pokazują, że konkurencja między nimi będzie „WŁĄCZONA”, co oznacza, że będzie zwycięzcą, a inne będą „WYŁĄCZONE”.
Poniżej przedstawiono niektóre sieci oparte na tej prostej koncepcji wykorzystujące uczenie się bez nadzoru.
Sieć Hamminga
W większości sieci neuronowych wykorzystujących uczenie się bez nadzoru istotne jest obliczenie odległości i wykonywanie porównań. Ten rodzaj sieci to sieć Hamminga, w której dla każdego danego wektora wejściowego byłaby zgrupowana w różne grupy. Oto kilka ważnych funkcji sieci Hamminga -
Lippmann rozpoczął pracę w sieciach Hamminga w 1987 roku.
Jest to sieć jednowarstwowa.
Wejścia mogą być binarne {0, 1} lub bipolarne {-1, 1}.
Wagi sieci są obliczane przez przykładowe wektory.
Jest to sieć o ustalonych obciążeniach, co oznacza, że obciążenia pozostaną takie same nawet podczas treningu.
Max Net
Jest to również sieć o stałej wadze, która służy jako podsieć do wybierania węzła o najwyższym wejściu. Wszystkie węzły są w pełni ze sobą połączone, a we wszystkich tych ważonych połączeniach istnieją symetryczne wagi.
Architektura
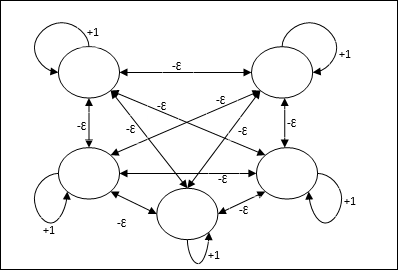
Wykorzystuje mechanizm, który jest procesem iteracyjnym, a każdy węzeł otrzymuje powstrzymujące dane wejściowe od wszystkich innych węzłów za pośrednictwem połączeń. Pojedynczy węzeł, którego wartość jest maksymalna, byłby aktywny lub zwycięski, a aktywacje wszystkich innych węzłów byłyby nieaktywne. Max Net używa funkcji aktywacji tożsamości z $$ f (x) \: = \: \ begin {cases} x & if \: x> 0 \\ 0 & if \: x \ leq 0 \ end {cases} $$
Zadanie tej sieci jest realizowane przez wagę samowzbudzenia równą +1 i wielkość wzajemnego hamowania, która jest ustawiona jako [0 <ɛ <$ \ frac {1} {m} $] gdzie “m” to całkowita liczba węzłów.
Konkurencyjne uczenie się w ANN
Dotyczy to nienadzorowanego szkolenia, w którym węzły wyjściowe próbują ze sobą konkurować, aby reprezentować wzorzec wejściowy. Aby zrozumieć tę zasadę uczenia się, będziemy musieli zrozumieć sieć konkurencyjną, która jest wyjaśniona w następujący sposób:
Podstawowa koncepcja sieci konkurencji
Ta sieć jest jak jednowarstwowa sieć sprzężenia zwrotnego z połączeniem zwrotnym między wyjściami. Połączenia między wyjściami są typu hamującego, co zaznaczono liniami przerywanymi, co oznacza, że zawodnicy nigdy się nie utrzymują.
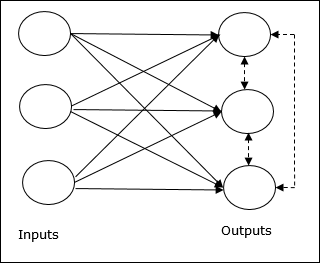
Podstawowa koncepcja reguły konkurencyjnej nauki
Jak wspomniano wcześniej, między węzłami wyjściowymi wystąpiłaby konkurencja, więc główna koncepcja jest taka - podczas treningu jednostka wyjściowa, która ma największą aktywację dla danego wzorca wejściowego, zostanie ogłoszona zwycięzcą. Ta zasada jest również nazywana zwycięzcą bierze wszystko, ponieważ tylko zwycięski neuron jest aktualizowany, a reszta neuronów pozostaje niezmieniona.
Sformułowanie matematyczne
Poniżej przedstawiono trzy ważne czynniki, które wpływają na matematyczne sformułowanie tej zasady uczenia się:
Warunek zwycięstwa
Załóżmy, że neuron yk chce być zwycięzcą, to byłby następujący warunek
$$ y_ {k} \: = \: \ begin {cases} 1 & if \: v_ {k}> v_ {j} \: for \: all \: \: j, \: j \: \ neq \ : k \\ 0 & poza tym \ end {cases} $$
Oznacza to, że jeśli jakikolwiek neuron, powiedzmy, yk chce wygrać, a następnie, powiedzmy, jego indukowane pole lokalne (wyjście jednostki sumującej) vk, musi być największym spośród wszystkich innych neuronów w sieci.
Stan sumy masy całkowitej
Innym ograniczeniem reguły konkurencyjnego uczenia się jest suma wag dla konkretnego neuronu wyjściowego, która wyniesie 1. Na przykład, jeśli rozważymy neuron k następnie
$$ \ Displaystyle \ sum \ limity_ {k} w_ {kj} \: = \: 1 \: \: \: \: dla \: all \: \: k $$
Zmiana wagi dla zwycięzcy
Jeśli neuron nie reaguje na wzorzec wejściowy, to w tym neuronie nie ma miejsca uczenie się. Jeśli jednak wygrywa dany neuron, odpowiednie wagi są korygowane w następujący sposób -
$$ \ Delta w_ {kj} \: = \: \ begin {cases} - \ alpha (x_ {j} \: - \: w_ {kj}), & if \: neuron \: k \: wins \\ 0 & if \: neuron \: k \: loss \ end {cases} $$
Tutaj $ \ alpha $ to współczynnik uczenia się.
To wyraźnie pokazuje, że faworyzujemy zwycięski neuron, dostosowując jego wagę, a jeśli neuron zostanie zgubiony, nie musimy przejmować się ponownym dostosowywaniem jego wagi.
Algorytm grupowania środków K-średnich
K-średnie to jeden z najpopularniejszych algorytmów klastrowania, w którym wykorzystujemy koncepcję procedury partycjonowania. Rozpoczynamy od wstępnej partycji i wielokrotnie przenosimy wzorce z jednego klastra do drugiego, aż uzyskamy satysfakcjonujący wynik.
Algorytm
Step 1 - Wybierz kpunkty jako początkowe centroidy. Zainicjujk prototypy (w1,…,wk), na przykład możemy je zidentyfikować za pomocą losowo wybranych wektorów wejściowych -
$$ W_ {j} \: = \: i_ {p}, \: \: \: gdzie \: j \: \ in \ lbrace1, ...., k \ rbrace \: and \: p \: \ w \ lbrace1, ...., n \ rbrace $$
Każdy klaster Cj jest związany z prototypem wj.
Step 2 - Powtarzaj krok 3-5, aż E przestanie maleć lub członkostwo w klastrze przestanie się zmieniać.
Step 3 - Dla każdego wektora wejściowego ip gdzie p ∈ {1,…,n}, położyć ip w klastrze Cj* z najbliższym prototypem wj* mający następujący związek
$$ | i_ {p} \: - \: w_ {j *} | \: \ leq \: | i_ {p} \: - \: w_ {j} |, \: j \: \ in \ lbrace1, ...., k \ rbrace $$
Step 4 - Dla każdego klastra Cj, gdzie j ∈ { 1,…,k}zaktualizuj prototyp wj być centroidem wszystkich próbek, które są obecnie w Cj więc to
$$ w_ {j} \: = \: \ sum_ {i_ {p} \ in C_ {j}} \ frac {i_ {p}} {| C_ {j} |} $$
Step 5 - Obliczyć całkowity błąd kwantyzacji w następujący sposób -
$$ E \: = \: \ sum_ {j = 1} ^ k \ sum_ {i_ {p} \ in w_ {j}} | i_ {p} \: - \: w_ {j} | ^ 2 $$
Neocognitron
Jest to wielowarstwowa sieć sprzężenia zwrotnego, która została opracowana przez Fukushimę w latach 80. Model ten jest oparty na uczeniu nadzorowanym i służy do wizualnego rozpoznawania wzorców, głównie znaków pisanych ręcznie. Jest to w zasadzie rozszerzenie sieci Cognitron, która została również opracowana przez Fukushimę w 1975 roku.
Architektura
Jest to sieć hierarchiczna, która składa się z wielu warstw i lokalnie w tych warstwach istnieje wzorzec połączeń.
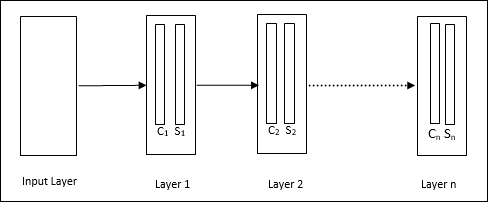
Jak widzieliśmy na powyższym diagramie, neokognitron jest podzielony na różne połączone ze sobą warstwy, a każda warstwa ma dwie komórki. Wyjaśnienie tych komórek jest następujące -
S-Cell - Nazywa się to prostą komórką, która jest trenowana, aby reagować na określony wzór lub grupę wzorców.
C-Cell- Nazywa się to komórką złożoną, która łączy dane wyjściowe z komórki S i jednocześnie zmniejsza liczbę jednostek w każdej tablicy. W innym sensie komórka C zastępuje wynik komórki S.
Algorytm treningowy
Stwierdzono, że trening neokognitronu postępuje warstwa po warstwie. Wagi z warstwy wejściowej do pierwszej warstwy są trenowane i zamrażane. Następnie trenowane są ciężary od pierwszej do drugiej warstwy i tak dalej. Wewnętrzne obliczenia między komórką S i komórką C zależą od wag pochodzących z poprzednich warstw. Dlatego możemy powiedzieć, że algorytm uczący zależy od obliczeń na komórkach S i C.
Obliczenia w komórce S.
Komórka S posiada sygnał pobudzający otrzymany z poprzedniej warstwy i posiada sygnały hamujące otrzymane w tej samej warstwie.
$$ \ theta = \: \ sqrt {\ sum \ sum t_ {i} c_ {i} ^ 2} $$
Tutaj, ti to stała waga i ci jest wyjściem z komórki C.
Skalowane dane wejściowe komórki S można obliczyć w następujący sposób -
$$ x \: = \: \ frac {1 \: + \: e} {1 \: + \: vw_ {0}} \: - \: 1 $$
Tutaj $ e \: = \: \ sum_i c_ {i} w_ {i} $
wi jest wagą skorygowaną z ogniwa C do ogniwa S.
w0 to waga regulowana pomiędzy wejściem a ogniwem S.
v jest pobudzającym wejściem z komórki C.
Aktywacja sygnału wyjściowego to:
$$ s \: = \: \ begin {cases} x, & if \: x \ geq 0 \\ 0, & if \: x <0 \ end {cases} $$
Obliczenia w komórce C.
Wkład netto warstwy C wynosi
$$ C \: = \: \ Displaystyle \ sum \ limits_i s_ {i} x_ {i} $$
Tutaj, si jest wyjściem z komórki S i xi jest stałą wagą z ogniwa S do ogniwa C.
Ostateczny wynik jest następujący -
$$ C_ {out} \: = \: \ begin {cases} \ frac {C} {a + C}, & if \: C> 0 \\ 0, & w przeciwnym razie \ end {cases} $$
Tutaj ‘a’ to parametr, który zależy od wydajności sieci.