Uczenie się i adaptacja
Jak wspomniano wcześniej, ANN jest całkowicie inspirowany sposobem, w jaki działa biologiczny układ nerwowy, czyli ludzki mózg. Najbardziej imponującą cechą ludzkiego mózgu jest uczenie się, stąd tę samą cechę nabywa SSN.
Czego się uczy w SSN?
Zasadniczo uczenie się oznacza dokonywanie i dostosowywanie zmiany samej w sobie, gdy zachodzi zmiana w środowisku. SSN to złożony system, a ściślej mówiąc, jest to złożony system adaptacyjny, który może zmieniać swoją wewnętrzną strukturę na podstawie przepływających przez niego informacji.
Dlaczego to jest ważne?
Będąc złożonym systemem adaptacyjnym, uczenie się w SSN oznacza, że jednostka przetwarzająca jest w stanie zmienić swoje zachowanie wejścia / wyjścia ze względu na zmianę środowiska. Znaczenie uczenia się w SSN wzrasta ze względu na stałą funkcję aktywacji, a także wektor wejścia / wyjścia, gdy konstruowana jest określona sieć. Teraz, aby zmienić zachowanie wejścia / wyjścia, musimy dostosować wagi.
Klasyfikacja
Można go zdefiniować jako proces uczenia się rozróżniania danych z próbek na różne klasy poprzez znajdowanie wspólnych cech między próbkami z tych samych klas. Na przykład, aby przeprowadzić szkolenie SSN, mamy kilka próbek treningowych z unikalnymi funkcjami, a do przeprowadzenia ich testów mamy kilka próbek testowych z innymi unikalnymi cechami. Klasyfikacja jest przykładem nadzorowanego uczenia się.
Zasady uczenia się sieci neuronowych
Wiemy, że podczas uczenia się SSN, aby zmienić zachowanie wejścia / wyjścia, musimy dostosować wagi. W związku z tym potrzebna jest metoda, za pomocą której można modyfikować wagi. Metody te nazywane są regułami uczenia się, które są po prostu algorytmami lub równaniami. Oto kilka reguł uczenia się dla sieci neuronowej -
Hebbian Learning Rule
Ta zasada, jedna z najstarszych i najprostszych, została wprowadzona przez Donalda Hebba w jego książce The Organization of Behaviour w 1949 roku. Jest to rodzaj uczenia się bez nadzoru.
Basic Concept - Zasada ta jest oparta na propozycji przedstawionej przez Hebba, który napisał -
„Kiedy akson komórki A jest wystarczająco blisko, aby wzbudzić komórkę B i wielokrotnie lub trwale bierze udział w jej odpalaniu, w jednej lub obu komórkach zachodzi pewien proces wzrostu lub zmiana metaboliczna, tak że wydajność A, gdy jedna z komórek odpala B , jest zwiększony."
Z powyższego postulatu możemy wywnioskować, że połączenia między dwoma neuronami mogą zostać wzmocnione, jeśli neurony będą odpalać w tym samym czasie, a osłabione, jeśli będą odpalać w różnym czasie.
Mathematical Formulation - Zgodnie z regułą Hebbian, następującą formułą jest zwiększanie wagi połączenia na każdym kroku czasowym.
$$ \ Delta w_ {ji} (t) \: = \: \ alpha x_ {i} (t) .y_ {j} (t) $$
Tutaj $ \ Delta w_ {ji} (t) $ = przyrost, o który zwiększa się waga połączenia w kroku czasowym t
$ \ alpha $ = dodatnia i stała stopa uczenia się
$ x_ {i} (t) $ = wartość wejściowa z neuronu pre-synaptycznego w kroku czasowym t
$ y_ {i} (t) $ = wyjście neuronu pre-synaptycznego w tym samym kroku czasowym t
Reguła uczenia się perceptronu
Ta reguła jest błędem korygującym algorytm nadzorowanego uczenia się jednowarstwowych sieci z wyprzedzeniem z liniową funkcją aktywacji, wprowadzony przez Rosenblatta.
Basic Concept- Ze względu na charakter nadzorowany, aby obliczyć błąd, należałoby porównać pożądaną / docelową wydajność z rzeczywistą wydajnością. Jeśli zostanie znaleziona jakaś różnica, należy zmienić wagę połączenia.
Mathematical Formulation - Aby wyjaśnić jego matematyczne sformułowanie, załóżmy, że mamy `` n '' liczbę skończonych wektorów wejściowych, x (n), wraz z pożądanym / docelowym wektorem wyjściowym t (n), gdzie n = 1 do N.
Teraz można obliczyć wyjście `` y '', jak wyjaśniono wcześniej na podstawie wkładu netto, a funkcję aktywacji zastosowaną do tego wkładu netto można wyrazić w następujący sposób -
$$ y \: = \: f (y_ {cal}) \: = \: \ begin {cases} 1, & y_ {in} \:> \: \ theta \\ 0, & y_ {in} \: \ leqslant \: \ theta \ end {cases} $$
Gdzie θ jest progiem.
Aktualizacji wagi można dokonać w dwóch następujących przypadkach -
Case I - kiedy t ≠ y, następnie
$$ w (nowe) \: = \: w (stare) \: + \; tx $$
Case II - kiedy t = y, następnie
Bez zmiany wagi
Reguła uczenia delta (reguła Widrowa-Hoffa)
Została wprowadzona przez Bernarda Widrowa i Marciana Hoffa, zwana także metodą najmniejszych średnich kwadratów (LMS), aby zminimalizować błąd we wszystkich wzorcach treningowych. Jest to rodzaj nadzorowanego algorytmu uczenia się z funkcją ciągłej aktywacji.
Basic Concept- Podstawą tej zasady jest podejście gradientowe, które trwa wiecznie. Reguła delta aktualizuje wagi synaptyczne, aby zminimalizować wkład netto do jednostki wyjściowej i wartość docelową.
Mathematical Formulation - Aby zaktualizować wagi synaptyczne, podaje się regułę delta przez
$$ \ Delta w_ {i} \: = \: \ alpha \ :. x_ {i} .e_ {j} $$
Tutaj $ \ Delta w_ {i} $ = zmiana wagi dla i- tego wzoru;
$ \ alpha $ = dodatnia i stała stopa uczenia się;
$ x_ {i} $ = wartość wejściowa z neuronu pre-synaptycznego;
$ e_ {j} $ = $ (t \: - \: y_ {in}) $, różnica między pożądanym / docelowym wyjściem a rzeczywistym wyjściem $ y_ {in} $
Powyższa reguła delta dotyczy tylko jednej jednostki wyjściowej.
Aktualizacji wagi można dokonać w dwóch następujących przypadkach -
Case-I - kiedy t ≠ y, następnie
$$ w (nowe) \: = \: w (stare) \: + \: \ Delta w $$
Case-II - kiedy t = y, następnie
Bez zmiany wagi
Reguła konkurencyjnego uczenia się (zwycięzca bierze wszystko)
Dotyczy to nienadzorowanego szkolenia, w którym węzły wyjściowe próbują ze sobą konkurować, aby reprezentować wzorzec wejściowy. Aby zrozumieć tę zasadę uczenia się, musimy zrozumieć konkurencyjną sieć, która jest podana w następujący sposób:
Basic Concept of Competitive Network- Ta sieć jest jak jednowarstwowa sieć sprzężenia zwrotnego z połączeniem zwrotnym między wyjściami. Połączenia między wyjściami są typu hamującego, pokazane liniami przerywanymi, co oznacza, że zawodnicy nigdy się nie utrzymują.
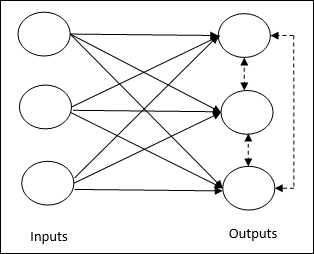
Basic Concept of Competitive Learning Rule- Jak wspomniano wcześniej, będzie konkurencja między węzłami wyjściowymi. Stąd główna koncepcja jest taka, że podczas treningu jednostka wyjściowa z najwyższą aktywacją danego wzorca wejściowego zostanie ogłoszona zwycięzcą. Ta zasada jest również nazywana zwycięzcą bierze wszystko, ponieważ tylko zwycięski neuron jest aktualizowany, a reszta neuronów pozostaje niezmieniona.
Mathematical formulation - Poniżej przedstawiono trzy ważne czynniki dla matematycznego sformułowania tej zasady uczenia się -
Condition to be a winner - Załóżmy, że jeśli neuron $ y_ {k} $ chce być zwycięzcą, to będzie następujący warunek -
$$ y_ {k} \: = \: \ begin {cases} 1 & if \: v_ {k} \:> \: v_ {j} \: for \: all \: j, \: j \: \ neq \: k \\ 0 & poza tym \ end {cases} $$
Oznacza to, że jeśli jakikolwiek neuron, powiedzmy $ y_ {k} $ , chce wygrać, to jego indukowane pole lokalne (wyjście jednostki sumowania), powiedzmy $ v_ {k} $, musi być największe spośród wszystkich innych neuronów w sieci.
Condition of sum total of weight - Kolejnym ograniczeniem w stosunku do reguły konkurencyjnego uczenia się jest to, że suma wag dla konkretnego neuronu wyjściowego wyniesie 1. Na przykład, jeśli rozważymy neuron k wtedy -
$$ \ Displaystyle \ sum \ limits_ {j} w_ {kj} \: = \: 1 \: \: \: \: \: \: \: \: \: dla \: all \: k $$
Change of weight for winner- Jeśli neuron nie reaguje na wzorzec wejściowy, to w tym neuronie nie odbywa się uczenie. Jeśli jednak wygrywa dany neuron, odpowiednie wagi są korygowane w następujący sposób
$$ \ Delta w_ {kj} \: = \: \ begin {cases} - \ alpha (x_ {j} \: - \: w_ {kj}), & if \: neuron \: k \: wins \\ 0, & if \: neuron \: k \: loss \ end {cases} $$
Tutaj $ \ alpha $ to współczynnik uczenia się.
To jasno pokazuje, że faworyzujemy zwycięski neuron, dostosowując jego wagę, a jeśli nastąpi utrata neuronu, nie musimy zawracać sobie głowy ponownym dostosowywaniem jego wagi.
Zasada uczenia się Outstar
Ta zasada, wprowadzona przez Grossberga, dotyczy uczenia się nadzorowanego, ponieważ znane są pożądane wyniki. Nazywa się to również uczeniem Grossberga.
Basic Concept- Zasada ta dotyczy neuronów ułożonych w warstwie. Jest specjalnie zaprojektowany, aby uzyskać pożądaną wydajnośćd warstwy p neurony.
Mathematical Formulation - Korekty wagi w tej regule są obliczane w następujący sposób
$$ \ Delta w_ {j} \: = \: \ alpha \ :( d \: - \: w_ {j}) $$
Tutaj d to pożądane wyjście neuronu, a $ \ alpha $ to szybkość uczenia się.