Optymalizacja z wykorzystaniem sieci Hopfield
Optymalizacja to działanie mające na celu uczynienie czegoś takiego jak projekt, sytuacja, zasoby i system tak efektywnymi, jak to tylko możliwe. Wykorzystując podobieństwo między funkcją kosztu a funkcją energii, możemy użyć silnie połączonych neuronów do rozwiązywania problemów optymalizacji. Takim rodzajem sieci neuronowej jest sieć Hopfield, która składa się z pojedynczej warstwy zawierającej jeden lub więcej w pełni połączonych neuronów powtarzających się. Można to wykorzystać do optymalizacji.
O czym należy pamiętać podczas korzystania z sieci Hopfield do optymalizacji -
Funkcja energetyczna musi być minimalna dla sieci.
Znajdzie satysfakcjonujące rozwiązanie zamiast wybierać jeden z zapisanych wzorów.
Jakość rozwiązania znalezionego przez sieć Hopfield zależy w dużym stopniu od początkowego stanu sieci.
Problem komiwojażera
Znalezienie najkrótszej trasy przebytej przez sprzedawcę jest jednym z problemów obliczeniowych, który można zoptymalizować wykorzystując sieć neuronową Hopfield.
Podstawowa koncepcja TSP
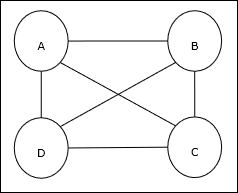
Problem komiwojażera (TSP) to klasyczny problem optymalizacyjny, w którym sprzedawca musi podróżować nmiasta, które są ze sobą połączone przy zachowaniu minimalnego kosztu i przebytej odległości. Na przykład sprzedawca musi podróżować przez zestaw 4 miast A, B, C, D, a celem jest znalezienie najkrótszej trasy okrężnej, ABC – D, tak aby zminimalizować koszty, które obejmują również koszty podróży z ostatnie miasto D do pierwszego miasta A.
Reprezentacja macierzy
Właściwie każdą wycieczkę po TSP w n-mieście można wyrazić jako n × n macierz, której ith wiersz opisuje ithlokalizacja miasta. Ta macierz,M, dla 4 miast A, B, C, D można wyrazić następująco -
$$ M = \ begin {bmatrix} A: & 1 & 0 & 0 & 0 \\ B: & 0 & 1 & 0 & 0 \\ C: & 0 & 0 & 1 & 0 \\ D: & 0 & 0 & 0 & 1 \ end {bmatrix} $$
Rozwiązanie firmy Hopfield Network
Rozważając rozwiązanie tego TSP przez sieć Hopfielda, każdemu węzłowi w sieci odpowiada jeden element macierzy.
Obliczanie funkcji energii
Aby było optymalnym rozwiązaniem, funkcja energii musi być minimalna. Na podstawie następujących ograniczeń możemy obliczyć funkcję energii w następujący sposób -
Ograniczenie-I
Pierwszym ograniczeniem, na podstawie którego obliczymy funkcję energii, jest to, że jeden element musi być równy 1 w każdym wierszu macierzy M a inne elementy w każdym wierszu muszą być równe 0ponieważ każde miasto może występować tylko w jednym miejscu w trasie TSP. To ograniczenie można zapisać matematycznie w następujący sposób -
$$ \ Displaystyle \ suma \ limity_ {j = 1} ^ n M_ {x, j} \: = \: 1 \: dla \: x \: \ in \: \ lbrace1, ..., n \ rbrace $ $
Teraz funkcja energii, która ma zostać zminimalizowana, w oparciu o powyższe ograniczenie, będzie zawierać człon proporcjonalny do -
$$ \ Displaystyle \ suma \ limit_ {x = 1} ^ n \ lewo (\ początek {tablica} {c} 1 \: - \: \ Displaystyle \ suma \ limity_ {j = 1} ^ n M_ {x, j } \ end {tablica} \ right) ^ 2 $$
Ograniczenie-II
Jak wiemy, w TSP jedno miasto może wystąpić w dowolnej pozycji w trasie, stąd w każdej kolumnie macierzy M, jeden element musi być równy 1, a inne elementy muszą być równe 0. To ograniczenie można matematycznie zapisać w następujący sposób -
$$ \ Displaystyle \ suma \ limity_ {x = 1} ^ n M_ {x, j} \: = \: 1 \: dla \: j \: \ in \: \ lbrace1, ..., n \ rbrace $ $
Teraz funkcja energii, która ma zostać zminimalizowana, w oparciu o powyższe ograniczenie, będzie zawierać człon proporcjonalny do -
$$ \ Displaystyle \ suma \ limity_ {j = 1} ^ n \ lewo (\ początek {tablica} {c} 1 \: - \: \ Displaystyle \ suma \ limit_ {x = 1} ^ n M_ {x, j } \ end {tablica} \ right) ^ 2 $$
Obliczanie funkcji kosztów
Załóżmy, że macierz kwadratową (n × n) oznaczony przez C oznacza macierz kosztów TSP dla n miasta, w których n > 0. Poniżej przedstawiono kilka parametrów podczas obliczania funkcji kosztu -
Cx, y - Element macierzy kosztów oznacza koszt dojazdu z miasta x do y.
Sąsiedztwo elementów A i B można pokazać za pomocą następującej zależności -
$$ M_ {x, i} \: = \: 1 \: \: and \: \: M_ {y, i \ pm 1} \: = \: 1 $$
Jak wiemy, w Matrixie wartość wyjściowa każdego węzła może wynosić 0 lub 1, stąd dla każdej pary miast A, B możemy dodać następujące wyrażenia do funkcji energii -
$$ \ Displaystyle \ suma \ limity_ {i = 1} ^ n C_ {x, y} M_ {x, i} (M_ {y, i + 1} \: + \: M_ {y, i-1}) $$
Na podstawie powyższej funkcji kosztu i wartości ograniczenia, funkcja energii końcowej E można podać w następujący sposób -
$$ E \: = \: \ Frac {1} {2} \ Displaystyle \ sum \ limit_ {i = 1} ^ n \ Displaystyle \ suma \ limity_ {x} \ Displaystyle \ suma \ limity_ {y \ neq x} C_ {x, y} M_ {x, i} (M_ {y, i + 1} \: + \: M_ {y, i-1}) \: + $$
$$ \: \ początek {bmatrix} \ gamma_ {1} \ displaystyle \ sum \ limit_ {x} \ lewo (\ początek {tablica} {c} 1 \: - \: \ displaystyle \ sum \ limity_ {i} M_ {x, i} \ koniec {tablica} \ po prawej) ^ 2 \: + \: \ gamma_ {2} \ displaystyle \ sum \ limit_ {i} \ lewo (\ początek {tablica} {c} 1 \: - \ : \ Displaystyle \ suma \ limity_ {x} M_ {x, i} \ koniec {tablica} \ po prawej) ^ 2 \ koniec {bmatrix} $$
Tutaj, γ1 i γ2 są dwiema stałymi ważenia.