Sztuczna sieć neuronowa - sieci Hopfielda
Sieć neuronowa Hopfield została wynaleziona przez dr. Johna J. Hopfielda w 1982 r. Składa się z pojedynczej warstwy zawierającej jeden lub więcej w pełni połączonych neuronów nawracających. Sieć Hopfield jest powszechnie używana do zadań auto-asocjacji i optymalizacji.
Dyskretna Sieć Hopfielda
Sieć Hopfielda, która działa w sposób dyskretny lub innymi słowy, można powiedzieć, że wzorce wejściowe i wyjściowe są dyskretnymi wektorami, które mogą mieć charakter binarny (0,1) lub bipolarny (+1, -1). Sieć ma symetryczne wagi bez połączeń samoczynnych tj.wij = wji i wii = 0.
Architektura
Oto kilka ważnych punktów, o których należy pamiętać w przypadku dyskretnej sieci Hopfield:
Model ten składa się z neuronów z jednym wyjściem odwracającym i jednym nieodwracającym.
Sygnał wyjściowy każdego neuronu powinien być wejściem innych neuronów, ale nie własnym.
Waga / siła połączenia jest reprezentowana przez wij.
Połączenia mogą być zarówno pobudzające, jak i hamujące. Byłoby pobudzające, gdyby sygnał wyjściowy neuronu był taki sam jak wejście, w przeciwnym razie hamowałby.
Wagi powinny być symetryczne, tj wij = wji
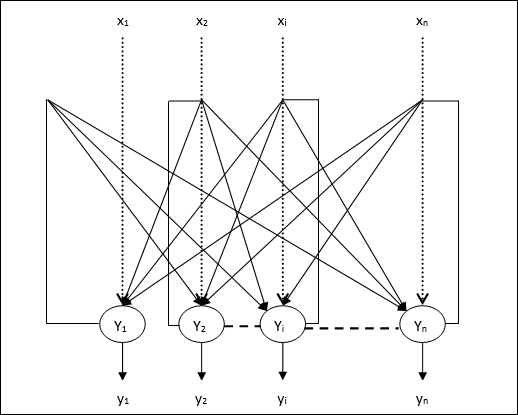
Dane wyjściowe z Y1 zamierzam Y2, Yi i Yn mieć ciężary w12, w1i i w1nodpowiednio. Podobnie, inne łuki mają na sobie ciężary.
Algorytm treningowy
Podczas treningu dyskretnej sieci Hopfield wagi będą aktualizowane. Jak wiemy, możemy mieć binarne wektory wejściowe, jak również bipolarne wektory wejściowe. W związku z tym w obu przypadkach aktualizacje wagi można przeprowadzić za pomocą następującej relacji
Case 1 - Wzorce wejść binarnych
Zestaw wzorców binarnych s(p), p = 1 to P
Tutaj, s(p) = s1(p), s2(p),..., si(p),..., sn(p)
Macierz wagi jest podana przez
$$ w_ {ij} \: = \: \ sum_ {p = 1} ^ P [2s_ {i} (p) - \: 1] [2s_ {j} (p) - \: 1] \: \: \: \: \: dla \: i \: \ neq \: j $$
Case 2 - Bipolarne wzorce wejściowe
Zestaw wzorców binarnych s(p), p = 1 to P
Tutaj, s(p) = s1(p), s2(p),..., si(p),..., sn(p)
Macierz wagi jest podana przez
$$ w_ {ij} \: = \: \ sum_ {p = 1} ^ P [s_ {i} (p)] [s_ {j} (p)] \: \: \: \: \: for \ : i \: \ neq \: j $$
Algorytm testowania
Step 1 - Zainicjuj wagi, które są uzyskiwane z algorytmu uczącego przy użyciu zasady Hebbiana.
Step 2 - Wykonaj kroki 3-9, jeśli aktywacje sieci nie są skonsolidowane.
Step 3 - Dla każdego wektora wejściowego Xwykonaj kroki 4-8.
Step 4 - Ustaw początkową aktywację sieci równą zewnętrznemu wektorowi wejściowemu X w następujący sposób -
$$ y_ {i} \: = \: x_ {i} \: \: \: dla \: i \: = \: 1 \: do \: n $$
Step 5 - Dla każdej jednostki Yiwykonaj kroki 6-9.
Step 6 - Obliczyć wejście netto sieci w następujący sposób -
$$ y_ {ini} \: = \: x_ {i} \: + \: \ displaystyle \ sum \ limits_ {j} y_ {j} w_ {ji} $$
Step 7 - Zastosuj aktywację w następujący sposób na wejściu netto, aby obliczyć moc -
$$ y_ {i} \: = \ begin {cases} 1 & if \: y_ {ini} \:> \: \ theta_ {i} \\ y_ {i} & if \: y_ {ini} \: = \: \ theta_ {i} \\ 0 & if \: y_ {ini} \: <\: \ theta_ {i} \ end {cases} $$
Tutaj $ \ theta_ {i} $ jest progiem.
Step 8 - Prześlij to wyjście yi do wszystkich innych jednostek.
Step 9 - Przetestuj połączenie w sieci.
Ocena funkcji energii
Funkcja energii jest definiowana jako funkcja, która jest powiązaną i nierosnącą funkcją stanu systemu.
Funkcja energii Ef, zwany także Lyapunov function określa stabilność dyskretnej sieci Hopfielda i charakteryzuje się następująco:
$$ E_ {f} \: = \: - \ Frac {1} {2} \ Displaystyle \ sum \ limit_ {i = 1} ^ n \ Displaystyle \ suma \ limity_ {j = 1} ^ n y_ {i} r_ {j} w_ {ij} \: - \: \ displaystyle \ sum \ limit_ {i = 1} ^ n x_ {i} y_ {i} \: + \: \ displaystyle \ sum \ limity_ {i = 1} ^ n \ theta_ {i} y_ {i} $$
Condition - W stabilnej sieci, gdy zmieni się stan węzła, powyższa funkcja energetyczna będzie się zmniejszać.
Załóżmy, że node i zmienił stan z $ y_i ^ {(k)} $ na $ y_i ^ {(k \: + \: 1)} $ , a następnie zmiana energii $ \ Delta E_ {f} $ jest określona przez następującą relację
$$ \ Delta E_ {f} \: = \: E_ {f} (y_i ^ {(k + 1)}) \: - \: E_ {f} (y_i ^ {(k)}) $$
$$ = \: - \ lewo (\ początek {tablica} {c} \ Displaystyle \ suma \ limity_ {j = 1} ^ n w_ {ij} y_i ^ {(k)} \: + \: x_ {i} \: - \: \ theta_ {i} \ end {array} \ right) (y_i ^ {(k + 1)} \: - \: y_i ^ {(k)}) $$
$$ = \: - \ :( net_ {i}) \ Delta y_ {i} $$
Tutaj $ \ Delta y_ {i} \: = \: y_i ^ {(k \: + \: 1)} \: - \: y_i ^ {(k)} $
Zmiana energii zależy od tego, że tylko jedna jednostka może aktualizować swoją aktywację na raz.
Ciągła Sieć Hopfielda
W porównaniu z dyskretną siecią Hopfielda, sieć ciągła ma czas jako zmienną ciągłą. Jest również używany w problemach z asocjacjami samochodowymi i optymalizacją, takich jak problem komiwojażera.
Model - Model lub architekturę można zbudować, dodając komponenty elektryczne, takie jak wzmacniacze, które mogą odwzorowywać napięcie wejściowe na napięcie wyjściowe za pomocą funkcji aktywacji sigmoidalnej.
Ocena funkcji energii
$$ E_f = \ Frac {1} {2} \ Displaystyle \ sum \ limity_ {i = 1} ^ n \ suma _ {\ substack {j = 1 \\ j \ ne i}} ^ n y_i y_j w_ {ij} - \ Displaystyle \ suma \ limity_ {i = 1} ^ n x_i y_i + \ Frac {1} {\ lambda} \ Displaystyle \ suma \ limity_ {i = 1} ^ n \ suma _ {\ substack {j = 1 \\ j \ ne i}} ^ n w_ {ij} g_ {ri} \ int_ {0} ^ {y_i} a ^ {- 1} (y) dy $$
Tutaj λ jest parametrem wzmocnienia i gri przewodność wejściowa.