Sztuczna sieć neuronowa - szybki przewodnik

Sieci neuronowe to równoległe urządzenia obliczeniowe, które w zasadzie są próbą stworzenia komputerowego modelu mózgu. Głównym celem jest opracowanie systemu do wykonywania różnych zadań obliczeniowych szybciej niż systemy tradycyjne. Zadania te obejmują rozpoznawanie i klasyfikację wzorców, aproksymację, optymalizację i grupowanie danych.

Co to jest sztuczna sieć neuronowa?

Sztuczna sieć neuronowa (ANN) to wydajny system obliczeniowy, którego motyw przewodni został zapożyczony z analogii biologicznych sieci neuronowych. SSN są również nazywane „sztucznymi systemami neuronowymi”, „równoległymi systemami przetwarzania rozproszonego” lub „systemami koneksjonistycznymi”. ANN pozyskuje duży zbiór jednostek, które są ze sobą połączone w pewien sposób, aby umożliwić komunikację między jednostkami. Jednostki te, nazywane również węzłami lub neuronami, to proste procesory działające równolegle.

Każdy neuron jest połączony z innym neuronem za pomocą łącza. Każdemu łączu przypisana jest waga zawierająca informacje o sygnale wejściowym. Jest to najbardziej przydatna informacja dla neuronów do rozwiązania konkretnego problemu, ponieważ ciężar zwykle pobudza lub hamuje przekazywany sygnał. Każdy neuron ma stan wewnętrzny, który nazywany jest sygnałem aktywacji. Sygnały wyjściowe, które powstają po połączeniu sygnałów wejściowych i reguły zadziałania, mogą być wysyłane do innych jednostek.

Krótka historia ANN

Historię SSN można podzielić na następujące trzy epoki -

ANN w latach czterdziestych do sześćdziesiątych XX wieku

Oto niektóre kluczowe wydarzenia z tej epoki -

• 1943 - Założono, że koncepcja sieci neuronowej zapoczątkowała pracę fizjologa Warrena McCullocha i matematyka Waltera Pittsa, kiedy w 1943 r. Modelowali prostą sieć neuronową za pomocą obwodów elektrycznych, aby opisać, jak mogą działać neurony w mózgu .

• 1949- W książce Donalda Hebba The Organization of Behavior wysunięto fakt, że wielokrotna aktywacja jednego neuronu przez inny zwiększa jego siłę za każdym razem, gdy są używane.

• 1956 - Sieć pamięci asocjacyjnej została wprowadzona przez Taylora.

• 1958 - Metoda uczenia się modelu neuronów McCullocha i Pittsa o nazwie Perceptron została wynaleziona przez Rosenblatta.

• 1960 - Bernard Widrow i Marcian Hoff opracowali modele nazwane „ADALINE” i „MADALINE”.

ANN w latach 1960-1980

Oto niektóre kluczowe wydarzenia z tej epoki -

• 1961 - Rosenblatt podjął nieudaną próbę, ale zaproponował schemat „wstecznej propagacji” sieci wielowarstwowych.

• 1964 - Taylor skonstruował obwód zwycięzca bierze wszystko z zahamowaniami między jednostkami wyjściowymi.

• 1969 - Perceptron wielowarstwowy (MLP) został wynaleziony przez Minsky'ego i Paperta.

• 1971 - Kohonen rozwinął wspomnienia asocjacyjne.

• 1976 - Stephen Grossberg i Gail Carpenter opracowali adaptacyjną teorię rezonansu.

ANN od 1980 do chwili obecnej

Oto niektóre kluczowe wydarzenia z tej epoki -

• 1982 - Głównym osiągnięciem było podejście Hopfielda do energii.

• 1985 - Maszyna Boltzmanna została opracowana przez Ackleya, Hintona i Sejnowskiego.

• 1986 - Rumelhart, Hinton i Williams wprowadzili uogólnioną regułę delta.

• 1988 - Kosko opracował Binary Associative Memory (BAM), a także przedstawił koncepcję Fuzzy Logic w SSN.

Z przeglądu historycznego wynika, że ​​w tej dziedzinie poczyniono znaczne postępy. Pojawiają się chipy oparte na sieciach neuronowych i opracowywane są aplikacje do rozwiązywania złożonych problemów. Z pewnością dzisiaj jest okres przejściowy dla technologii sieci neuronowych.

Biological Neuron

Komórka nerwowa (neuron) to specjalna komórka biologiczna, która przetwarza informacje. Według szacunków istnieje ogromna liczba neuronów, około 10 ¹¹ z licznymi połączeniami, około 10 ¹⁵ .

Schemat

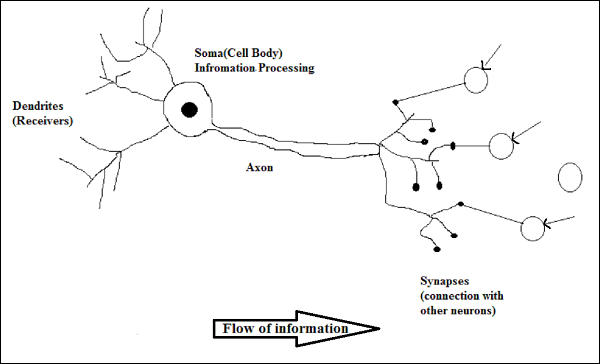
Działanie neuronu biologicznego

Jak pokazano na powyższym schemacie, typowy neuron składa się z następujących czterech części, za pomocą których możemy wyjaśnić jego działanie -

• Dendrites- Są to gałęzie przypominające drzewo, odpowiedzialne za odbieranie informacji od innych neuronów, z którymi jest połączony. W innym sensie możemy powiedzieć, że są jak uszy neuronu.

• Soma - Jest to ciało komórkowe neuronu i odpowiada za przetwarzanie informacji, które otrzymały z dendrytów.

• Axon - To jest jak kabel, przez który neurony przesyłają informacje.

• Synapses - Jest to połączenie między aksonem a innymi dendrytami neuronów.

ANN kontra BNN

Zanim przyjrzymy się różnicom między sztuczną siecią neuronową (ANN) a biologiczną siecią neuronową (BNN), przyjrzyjmy się podobieństwom opartym na terminologii między nimi.

Biologiczna sieć neuronowa (BNN)	Sztuczna sieć neuronowa (ANN)
Soma	Węzeł
Dendryty	Wejście
Synapsa	Wagi lub połączenia międzysystemowe
Axon	Wynik

Poniższa tabela przedstawia porównanie ANN i BNN na podstawie niektórych wymienionych kryteriów.

Kryteria	BNN	ANN
Processing	Masywnie równoległe, powolne, ale lepsze niż ANN	Masywnie równoległe, szybkie, ale gorsze niż BNN
Size	10 11 neuronów i 10 15 połączeń	10 2 do 10 4 węzłów (zależy głównie od typu aplikacji i projektanta sieci)
Learning	Potrafią tolerować dwuznaczność	Aby tolerować niejednoznaczność, wymagane są bardzo precyzyjne, ustrukturyzowane i sformatowane dane
Fault tolerance	Wydajność spada nawet z częściowym uszkodzeniem	Jest zdolny do solidnej wydajności, dlatego może być odporny na uszkodzenia
Storage capacity	Przechowuje informacje w synapsie	Przechowuje informacje w ciągłych lokalizacjach pamięci

Model sztucznej sieci neuronowej

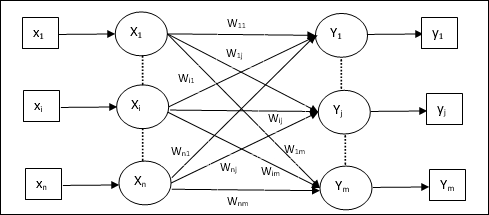
Poniższy diagram przedstawia ogólny model SSN, po którym następuje jego przetwarzanie.

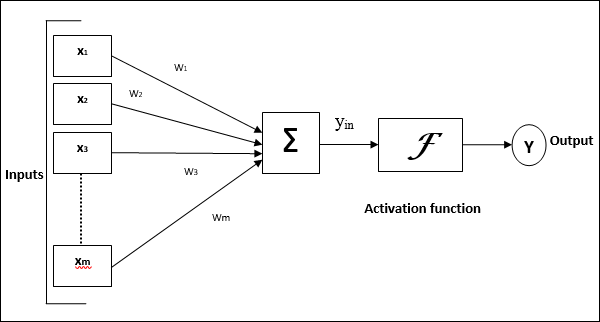
Dla powyższego ogólnego modelu sztucznej sieci neuronowej wejście netto można obliczyć w następujący sposób -

$$ y_ {in} \: = \: x_ {1} .w_ {1} \: + \: x_ {2} .w_ {2} \: + \: x_ {3} .w_ {3} \: \ dotso \: x_ {m.} .w_ {m.} $$

tj. wejście netto $ y_ {in} \: = \: \ sum_i ^ m \: x_ {i} .w_ {i} $

Wyjście można obliczyć, stosując funkcję aktywacji na wejściu netto.

$$ Y \: = \: F (y_ {in}) $$

Wyjście = funkcja (obliczony wkład netto)

Przetwarzanie SSN zależy od następujących trzech elementów składowych -

• Topologia sieci
• Korekty wag lub nauka
• Funkcje aktywacji

W tym rozdziale omówimy szczegółowo te trzy elementy składowe SSN

Topologia sieci

Topologia sieci to układ sieci wraz z jej węzłami i liniami łączącymi. Zgodnie z topologią SSN można podzielić na następujące rodzaje -

Sieć przekazująca

Jest to sieć jednorazowa z jednostkami / węzłami przetwarzającymi w warstwach, a wszystkie węzły w warstwie są połączone z węzłami warstw poprzednich. Połączenie ma różną wagę. Brak pętli sprzężenia zwrotnego oznacza, że ​​sygnał może przepływać tylko w jednym kierunku, od wejścia do wyjścia. Można go podzielić na dwa typy -

• Single layer feedforward network- Koncepcja jest oparta na sprzężeniu zwrotnym ANN, który ma tylko jedną ważoną warstwę. Innymi słowy, możemy powiedzieć, że warstwa wejściowa jest w pełni połączona z warstwą wyjściową.

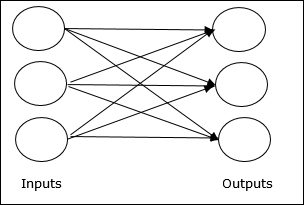
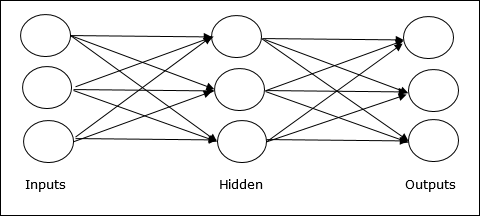
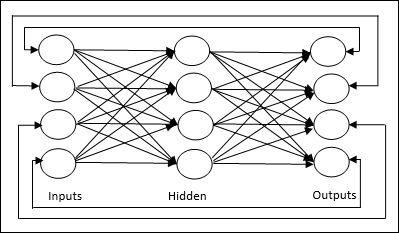
• Multilayer feedforward network- Koncepcja jest oparta na sprzężeniu zwrotnym ANN mającym więcej niż jedną ważoną warstwę. Ponieważ ta sieć ma jedną lub więcej warstw między warstwą wejściową a wyjściową, nazywa się ją warstwami ukrytymi.

Sieć opinii

Jak sama nazwa wskazuje, sieć sprzężenia zwrotnego ma ścieżki sprzężenia zwrotnego, co oznacza, że ​​sygnał może płynąć w obu kierunkach za pomocą pętli. To sprawia, że ​​jest to nieliniowy układ dynamiczny, który zmienia się w sposób ciągły, aż do osiągnięcia stanu równowagi. Można go podzielić na następujące typy -

• Recurrent networks- Są to sieci sprzężenia zwrotnego z zamkniętymi pętlami. Poniżej przedstawiono dwa typy powtarzających się sieci.

• Fully recurrent network - Jest to najprostsza architektura sieci neuronowej, ponieważ wszystkie węzły są połączone ze wszystkimi innymi, a każdy węzeł działa zarówno jako wejście, jak i wyjście.

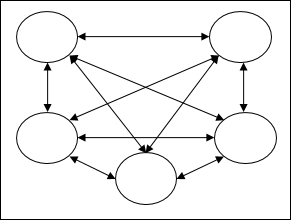
• Jordan network - Jest to sieć z zamkniętą pętlą, w której wyjście będzie ponownie przesyłane do wejścia jako sprzężenie zwrotne, jak pokazano na poniższym schemacie.

Korekty wag lub nauka

Uczenie się w sztucznej sieci neuronowej jest metodą modyfikowania wag połączeń między neuronami określonej sieci. Uczenie się w SSN można podzielić na trzy kategorie: uczenie się nadzorowane, uczenie się bez nadzoru i uczenie się ze wzmocnieniem.

Nadzorowana nauka

Jak sama nazwa wskazuje, ten rodzaj nauki odbywa się pod okiem nauczyciela. Ten proces uczenia się jest zależny.

Podczas uczenia SSN w ramach uczenia nadzorowanego wektor wejściowy jest prezentowany w sieci, co daje wektor wyjściowy. Ten wektor wyjściowy jest porównywany z pożądanym wektorem wyjściowym. Sygnał błędu jest generowany, jeśli istnieje różnica między rzeczywistym wyjściem a żądanym wektorem wyjściowym. Na podstawie tego sygnału błędu wagi są korygowane, aż rzeczywista moc wyjściowa zostanie dopasowana do żądanej mocy.

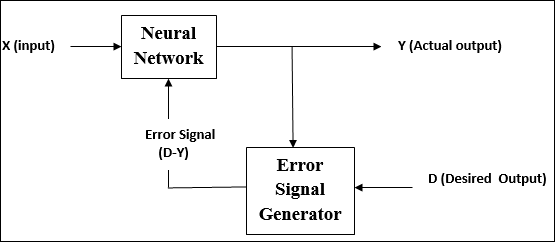
Uczenie się bez nadzoru

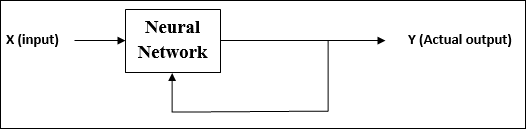
Jak sama nazwa wskazuje, ten rodzaj nauki odbywa się bez nadzoru nauczyciela. Ten proces uczenia się jest niezależny.

Podczas uczenia SSN w ramach uczenia się bez nadzoru wektory wejściowe podobnego typu są łączone w klastry. Po zastosowaniu nowego wzorca wejściowego sieć neuronowa daje odpowiedź wyjściową wskazującą klasę, do której należy wzorzec wejściowy.

Nie ma informacji zwrotnej ze środowiska, co powinno być pożądanym wyjściem i czy jest poprawne lub niepoprawne. Dlatego w tego typu uczeniu się sama sieć musi odkryć wzorce i cechy z danych wejściowych oraz relację danych wejściowych do danych wyjściowych.

Uczenie się ze wzmocnieniem

Jak sama nazwa wskazuje, ten rodzaj uczenia się służy do wzmacniania lub wzmacniania sieci w zakresie niektórych krytycznych informacji. Ten proces uczenia się jest podobny do nadzorowanego uczenia się, jednak możemy mieć bardzo mniej informacji.

Podczas szkolenia sieci w ramach uczenia się przez wzmacnianie, sieć otrzymuje informacje zwrotne od środowiska. To sprawia, że ​​jest trochę podobny do nadzorowanego uczenia się. Jednak uzyskana tutaj informacja zwrotna ma charakter ewaluacyjny, a nie pouczający, co oznacza, że ​​nie ma nauczyciela takiego jak w uczeniu się nadzorowanym. Po otrzymaniu informacji zwrotnej sieć dokonuje korekty wag, aby w przyszłości uzyskać lepsze informacje o krytykach.

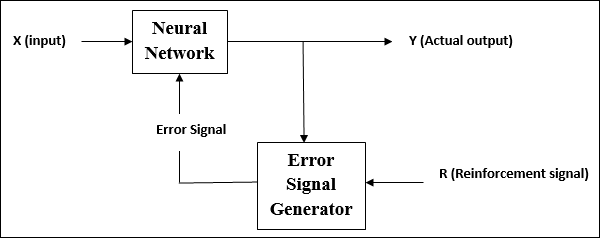
Funkcje aktywacji

Można to zdefiniować jako dodatkową siłę lub wysiłek zastosowany na wejściu w celu uzyskania dokładnego wyniku. W ANN możemy również zastosować funkcje aktywacji na wejściu, aby uzyskać dokładny wynik. Poniżej przedstawiono niektóre interesujące funkcje aktywacji -

Liniowa funkcja aktywacji

Jest również nazywany funkcją identyfikacji, ponieważ nie wykonuje edycji danych wejściowych. Można go zdefiniować jako -

$$ F (x) \: = \: x $$

Funkcja aktywacji esicy

Jest dwojakiego rodzaju:

• Binary sigmoidal function- Ta funkcja aktywacji przeprowadza edycję danych wejściowych od 0 do 1. Ma charakter pozytywny. Jest zawsze ograniczony, co oznacza, że ​​jego moc wyjściowa nie może być mniejsza niż 0 i większa niż 1. Ma również charakter ściśle rosnący, co oznacza, że ​​większe wejście byłoby wyjściem. Można go zdefiniować jako

  $$ F (x) \: = \: sigm (x) \: = \: \ frac {1} {1 \: + \: exp (-x)} $$

• Bipolar sigmoidal function- Ta funkcja aktywacji wykonuje edycję danych wejściowych w zakresie od -1 do 1. Może mieć charakter pozytywny lub negatywny. Jest zawsze ograniczony, co oznacza, że ​​jego wartość wyjściowa nie może być mniejsza niż -1 i większa niż 1. Ma również charakter ściśle rosnący, podobnie jak funkcja sigmoidalna. Można go zdefiniować jako

  $$ F (x) \: = \: sigm (x) \: = \: \ frac {2} {1 \: + \: exp (-x)} \: - \: 1 \: = \: \ frac {1 \: - \: exp (x)} {1 \: + \: exp (x)} $$

Jak wspomniano wcześniej, ANN jest całkowicie inspirowany sposobem, w jaki działa biologiczny układ nerwowy, czyli ludzki mózg. Najbardziej imponującą cechą ludzkiego mózgu jest uczenie się, stąd tę samą cechę nabywa SSN.

Czego się uczy w SSN?

Zasadniczo uczenie się oznacza dokonywanie i dostosowywanie zmiany samej w sobie, gdy zachodzi zmiana w środowisku. SSN to złożony system, a ściślej mówiąc, jest to złożony system adaptacyjny, który może zmieniać swoją wewnętrzną strukturę na podstawie przepływających przez niego informacji.

Dlaczego to jest ważne?

Będąc złożonym systemem adaptacyjnym, uczenie się w SSN oznacza, że ​​jednostka przetwarzająca jest w stanie zmienić swoje zachowanie wejścia / wyjścia ze względu na zmianę środowiska. Znaczenie uczenia się w SSN wzrasta ze względu na stałą funkcję aktywacji, a także wektor wejścia / wyjścia, gdy konstruowana jest określona sieć. Teraz, aby zmienić zachowanie wejścia / wyjścia, musimy dostosować wagi.

Klasyfikacja

Można go zdefiniować jako proces uczenia się rozróżniania danych z próbek na różne klasy poprzez znajdowanie wspólnych cech między próbkami z tych samych klas. Na przykład, aby przeprowadzić szkolenie SSN, mamy kilka próbek treningowych z unikalnymi funkcjami, a do przeprowadzenia ich testów mamy kilka próbek testowych z innymi unikalnymi cechami. Klasyfikacja jest przykładem nadzorowanego uczenia się.

Zasady uczenia się sieci neuronowej

Wiemy, że podczas uczenia się SSN, aby zmienić zachowanie wejścia / wyjścia, musimy dostosować wagi. Dlatego potrzebna jest metoda, za pomocą której można modyfikować wagi. Metody te nazywane są regułami uczenia się, które są po prostu algorytmami lub równaniami. Oto kilka reguł uczenia się dla sieci neuronowej -

Hebbian Learning Rule

Ta zasada, jedna z najstarszych i najprostszych, została wprowadzona przez Donalda Hebba w jego książce The Organization of Behaviour w 1949 roku. Jest to rodzaj uczenia się bez nadzoru.

Basic Concept - Zasada ta jest oparta na propozycji przedstawionej przez Hebba, który napisał -

„Kiedy akson komórki A jest wystarczająco blisko, aby wzbudzić komórkę B i wielokrotnie lub trwale bierze udział w jej odpalaniu, w jednej lub obu komórkach zachodzi pewien proces wzrostu lub zmiana metaboliczna, tak że wydajność A, gdy jedna z komórek odpala B , jest zwiększony."

Z powyższego postulatu możemy wywnioskować, że połączenia między dwoma neuronami mogą zostać wzmocnione, jeśli neurony będą odpalać w tym samym czasie, a osłabione, jeśli będą odpalać w różnym czasie.

Mathematical Formulation - Zgodnie z hebbijską zasadą uczenia się, następująca jest formuła zwiększania wagi połączenia na każdym kroku czasowym.

$$ \ Delta w_ {ji} (t) \: = \: \ alpha x_ {i} (t) .y_ {j} (t) $$

Tutaj $ \ Delta w_ {ji} (t) $ ⁡ = przyrost, o który zwiększa się waga połączenia w kroku czasowym t

$ \ alpha $ = dodatnia i stała stopa uczenia się

$ x_ {i} (t) $ = wartość wejściowa z neuronu pre-synaptycznego w kroku czasowym t

$ y_ {i} (t) $ = wyjście neuronu pre-synaptycznego w tym samym kroku czasowym t

Reguła uczenia się perceptronu

Ta reguła jest błędem korygującym algorytm nadzorowanego uczenia się jednowarstwowych sieci z wyprzedzeniem z liniową funkcją aktywacji, wprowadzony przez Rosenblatta.

Basic Concept- Ze względu na charakter nadzorowany, aby obliczyć błąd, należałoby porównać pożądaną / docelową wydajność z rzeczywistą wydajnością. Jeśli zostanie znaleziona jakaś różnica, należy zmienić wagę połączenia.

Mathematical Formulation - Aby wyjaśnić jego matematyczne sformułowanie, załóżmy, że mamy `` n '' liczbę skończonych wektorów wejściowych, x (n), wraz z pożądanym / docelowym wektorem wyjściowym t (n), gdzie n = 1 do N.

Teraz można obliczyć wyjście `` y '', jak wyjaśniono wcześniej na podstawie wkładu netto, a funkcję aktywacji zastosowaną do tego wkładu netto można wyrazić w następujący sposób -

$$ y \: = \: f (y_ {cal}) \: = \: \ begin {cases} 1, & y_ {in} \:> \: \ theta \\ 0, & y_ {in} \: \ leqslant \: \ theta \ end {cases} $$

Gdzie θ jest progiem.

Aktualizacji wagi można dokonać w dwóch następujących przypadkach -

Case I - kiedy t ≠ y, następnie

$$ w (nowe) \: = \: w (stare) \: + \; tx $$

Case II - kiedy t = y, następnie

Bez zmiany wagi

Reguła uczenia delta (reguła Widrowa-Hoffa)

Została wprowadzona przez Bernarda Widrowa i Marciana Hoffa, zwana także metodą najmniejszych średnich kwadratów (LMS), aby zminimalizować błąd we wszystkich wzorcach treningowych. Jest to rodzaj nadzorowanego algorytmu uczenia się z funkcją ciągłej aktywacji.

Basic Concept- Podstawą tej zasady jest podejście gradientowe, które trwa wiecznie. Reguła delta aktualizuje wagi synaptyczne, aby zminimalizować wkład netto do jednostki wyjściowej i wartość docelową.

Mathematical Formulation - Aby zaktualizować wagi synaptyczne, podaje się regułę delta przez

$$ \ Delta w_ {i} \: = \: \ alpha \ :. x_ {i} .e_ {j} $$

Tutaj $ \ Delta w_ {i} $ = zmiana wagi dla i- ^tego ⁡ wzoru;

$ \ alpha $ = dodatnia i stała stopa uczenia się;

$ x_ {i} $ = wartość wejściowa z neuronu pre-synaptycznego;

$ e_ {j} $ = $ (t \: - \: y_ {in}) $, różnica między pożądanym / docelowym wyjściem a rzeczywistym wyjściem ⁡ $ y_ {in} $

Powyższa reguła delta dotyczy tylko jednej jednostki wyjściowej.

Aktualizacji wagi można dokonać w dwóch następujących przypadkach -

Case-I - kiedy t ≠ y, następnie

$$ w (nowe) \: = \: w (stare) \: + \: \ Delta w $$

Case-II - kiedy t = y, następnie

Bez zmiany wagi

Reguła konkurencyjnego uczenia się (zwycięzca bierze wszystko)

Dotyczy to nienadzorowanego szkolenia, w którym węzły wyjściowe próbują ze sobą konkurować, aby reprezentować wzorzec wejściowy. Aby zrozumieć tę zasadę uczenia się, musimy zrozumieć konkurencyjną sieć, która jest podana w następujący sposób:

Basic Concept of Competitive Network- Ta sieć jest jak jednowarstwowa sieć sprzężenia zwrotnego z połączeniem zwrotnym między wyjściami. Połączenia między wyjściami są typu hamującego, pokazane liniami przerywanymi, co oznacza, że ​​zawodnicy nigdy się nie utrzymują.

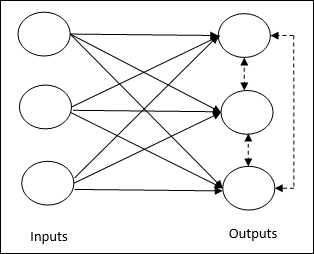
Basic Concept of Competitive Learning Rule- Jak wspomniano wcześniej, będzie konkurencja między węzłami wyjściowymi. Stąd główna koncepcja polega na tym, że podczas treningu jednostka wyjściowa z największą aktywacją dla danego wzorca wejściowego zostanie ogłoszona zwycięzcą. Ta zasada jest również nazywana zwycięzcą bierze wszystko, ponieważ tylko zwycięski neuron jest aktualizowany, a reszta neuronów pozostaje niezmieniona.

Mathematical formulation - Poniżej przedstawiono trzy ważne czynniki dla matematycznego sformułowania tej zasady uczenia się -

• Condition to be a winner - Załóżmy, że jeśli neuron $ y_ {k} $ ⁡ ⁡ chce być zwycięzcą, to będzie następujący warunek -

  $$ y_ {k} \: = \: \ begin {cases} 1 & if \: v_ {k} \:> \: v_ {j} \: for \: all \: j, \: j \: \ neq \: k \\ 0 & poza tym \ end {cases} $$

Oznacza to, że jeśli jakikolwiek neuron, powiedzmy $ y_ {k} $ ⁡, chce wygrać, to jego indukowane pole lokalne (wyjście jednostki sumowania), powiedzmy $ v_ {k} $, musi być największe spośród wszystkich innych neuronów w sieci.

• Condition of sum total of weight - Kolejnym ograniczeniem w stosunku do reguły uczenia się konkurencyjnego jest to, że suma wag dla konkretnego neuronu wyjściowego wyniesie 1. Na przykład, jeśli rozważymy neuron k wtedy -

  $$ \ Displaystyle \ sum \ limits_ {j} w_ {kj} \: = \: 1 \: \: \: \: \: \: \: \: \: dla \: all \: k $$

• Change of weight for winner- Jeśli neuron nie reaguje na wzorzec wejściowy, to w tym neuronie nie odbywa się uczenie. Jeśli jednak wygrywa dany neuron, odpowiednie wagi są korygowane w następujący sposób

  $$ \ Delta w_ {kj} \: = \: \ begin {cases} - \ alpha (x_ {j} \: - \: w_ {kj}), & if \: neuron \: k \: wins \\ 0, & if \: neuron \: k \: loss \ end {cases} $$

Tutaj $ \ alpha $ to współczynnik uczenia się.

To wyraźnie pokazuje, że faworyzujemy zwycięski neuron, dostosowując jego wagę, a jeśli nastąpi utrata neuronu, nie musimy przejmować się ponownym dostosowywaniem jego wagi.

Zasada uczenia się Outstar

Ta zasada, wprowadzona przez Grossberga, dotyczy uczenia się nadzorowanego, ponieważ znane są pożądane wyniki. Nazywa się to również uczeniem Grossberga.

Basic Concept- Zasada ta dotyczy neuronów ułożonych w warstwie. Jest specjalnie zaprojektowany, aby uzyskać pożądaną wydajnośćd warstwy p neurony.

Mathematical Formulation - Korekty wagi w tej regule są obliczane w następujący sposób

$$ \ Delta w_ {j} \: = \: \ alpha \ :( d \: - \: w_ {j}) $$

Tutaj d to pożądane wyjście neuronu, a $ \ alpha $ to szybkość uczenia się.

Jak sama nazwa wskazuje, supervised learningodbywa się pod opieką nauczyciela. Ten proces uczenia się jest zależny. Podczas uczenia SSN w ramach nadzorowanego uczenia się wektor wejściowy jest przedstawiany sieci, która wygeneruje wektor wyjściowy. Ten wektor wyjściowy jest porównywany z pożądanym / docelowym wektorem wyjściowym. Sygnał błędu jest generowany, jeśli istnieje różnica między rzeczywistym wyjściem a żądanym / docelowym wektorem wyjściowym. Na podstawie tego sygnału błędu wagi byłyby korygowane, aż rzeczywista moc wyjściowa zostanie dopasowana do żądanej mocy.

Perceptron

Opracowany przez Franka Rosenblatta przy użyciu modelu McCullocha i Pittsa, perceptron jest podstawową jednostką operacyjną sztucznych sieci neuronowych. Wykorzystuje regułę uczenia nadzorowanego i jest w stanie podzielić dane na dwie klasy.

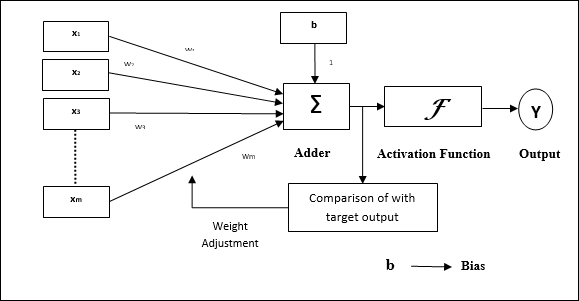
Charakterystyka operacyjna perceptronu: składa się z pojedynczego neuronu z dowolną liczbą wejść wraz z regulowanymi wagami, ale wyjście neuronu wynosi 1 lub 0 w zależności od progu. Składa się również z odchylenia, którego waga zawsze wynosi 1. Poniższy rysunek przedstawia schematyczny obraz perceptronu.

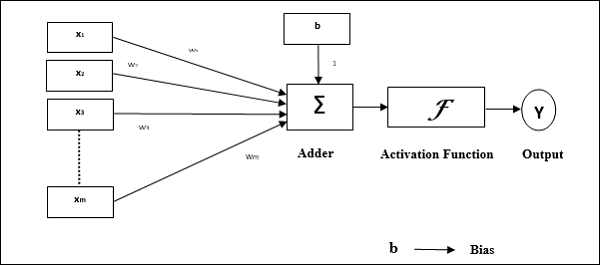
Zatem Perceptron ma następujące trzy podstawowe elementy -

• Links - Miałby zestaw łączy połączeniowych, który ma wagę zawierającą odchylenie zawsze o wadze 1.

• Adder - Dodaje dane wejściowe po ich pomnożeniu przez ich odpowiednie wagi.

• Activation function- Ogranicza wydajność neuronu. Najbardziej podstawową funkcją aktywacji jest funkcja krokowa Heaviside, która ma dwa możliwe wyjścia. Ta funkcja zwraca 1, jeśli dane wejściowe są dodatnie, i 0, jeśli dane wejściowe są ujemne.

Algorytm treningowy

Sieć perceptronów może być przeszkolona dla jednej jednostki wyjściowej, jak również wielu jednostek wyjściowych.

Algorytm uczący dla pojedynczego urządzenia wyjściowego

Step 1 - Zainicjuj następujące elementy, aby rozpocząć szkolenie -

• Weights
• Bias
• Kurs nauki $ \ alpha $

W celu ułatwienia i uproszczenia obliczeń wagi i odchylenie należy ustawić na 0, a współczynnik uczenia się na 1.

Step 2 - Kontynuuj krok 3-8, jeśli warunek zatrzymania nie jest prawdziwy.

Step 3 - Kontynuuj krok 4-6 dla każdego wektora szkoleniowego x.

Step 4 - Aktywuj każdą jednostkę wejściową w następujący sposób -

$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: do \: n) $$

Step 5 - Teraz uzyskaj dane wejściowe netto z następującą zależnością -

$$ y_ {in} \: = \: b \: + \: \ Displaystyle \ suma \ limit_ {i} ^ n x_ {i}. \: w_ {i} $$

Tutaj ‘b’ jest stronniczość i ‘n’ to całkowita liczba neuronów wejściowych.

Step 6 - Zastosuj następującą funkcję aktywacji, aby uzyskać ostateczne wyjście.

$$ f (y_ {in}) \: = \: \ begin {cases} 1 & if \: y_ {in} \:> \: \ theta \\ 0 & if \: - \ theta \: \ leqslant \ : y_ {in} \: \ leqslant \: \ theta \\ - 1 & if \: y_ {in} \: <\: - \ theta \ end {cases} $$

Step 7 - Dostosuj wagę i odchylenie w następujący sposób -

Case 1 - jeśli y ≠ t następnie,

$$ w_ {i} (nowe) \: = \: w_ {i} (stare) \: + \: \ alpha \: tx_ {i} $$

$$ b (nowe) \: = \: b (stare) \: + \: \ alpha t $$

Case 2 - jeśli y = t następnie,

$$ w_ {i} (nowe) \: = \: w_ {i} (stare) $$

$$ b (nowy) \: = \: b (stary) $$

Tutaj ‘y’ to rzeczywista wydajność i ‘t’ jest pożądanym / docelowym wyjściem.

Step 8 - Sprawdź stan zatrzymania, który wystąpiłby, gdyby nie nastąpiła zmiana wagi.

Algorytm uczący dla wielu jednostek wyjściowych

Poniższy diagram przedstawia architekturę perceptronu dla wielu klas wyjściowych.

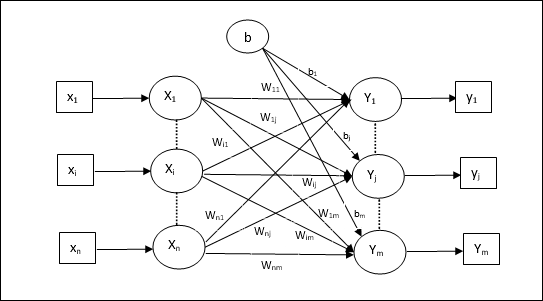
Step 1 - Zainicjuj następujące elementy, aby rozpocząć szkolenie -

• Weights
• Bias
• Kurs nauki $ \ alpha $

W celu ułatwienia i uproszczenia obliczeń wagi i odchylenie należy ustawić na 0, a współczynnik uczenia się na 1.

Step 2 - Kontynuuj krok 3-8, jeśli warunek zatrzymania nie jest prawdziwy.

Step 3 - Kontynuuj krok 4-6 dla każdego wektora szkoleniowego x.

Step 4 - Aktywuj każdą jednostkę wejściową w następujący sposób -

$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: do \: n) $$

Step 5 - Uzyskaj dane wejściowe netto z następującą zależnością -

$$ y_ {in} \: = \: b \: + \: \ Displaystyle \ sum \ limity_ {i} ^ n x_ {i} \: w_ {ij} $$

Tutaj ‘b’ jest stronniczość i ‘n’ to całkowita liczba neuronów wejściowych.

Step 6 - Zastosuj następującą funkcję aktywacji, aby uzyskać ostateczną moc wyjściową dla każdej jednostki wyjściowej j = 1 to m -

$$ f (y_ {in}) \: = \: \ begin {cases} 1 & if \: y_ {inject} \:> \: \ theta \\ 0 & if \: - \ theta \: \ leqslant \ : y_ {inject} \: \ leqslant \: \ theta \\ - 1 & if \: y_ {inject} \: <\: - \ theta \ end {cases} $$

Step 7 - Dostosuj wagę i odchylenie x = 1 to n i j = 1 to m w następujący sposób -

Case 1 - jeśli y_j ≠ t_j następnie,

$$ w_ {ij} (nowy) \: = \: w_ {ij} (stary) \: + \: \ alpha \: t_ {j} x_ {i} $$

$$ b_ {j} (nowe) \: = \: b_ {j} (stare) \: + \: \ alpha t_ {j} $$

Case 2 - jeśli y_j = t_j następnie,

$$ w_ {ij} (nowy) \: = \: w_ {ij} (stary) $$

$$ b_ {j} (nowe) \: = \: b_ {j} (stare) $$

Tutaj ‘y’ to rzeczywista wydajność i ‘t’ jest pożądanym / docelowym wyjściem.

Step 8 - Sprawdź stan zatrzymania, który wystąpi, gdy waga nie ulegnie zmianie.

Adaptacyjny neuron liniowy (Adaline)

Adaline, czyli Adaptive Linear Neuron, to sieć składająca się z jednej jednostki liniowej. Został opracowany przez Widrow i Hoff w 1960 roku. Niektóre ważne punkty dotyczące Adaline są następujące -

• Wykorzystuje funkcję aktywacji bipolarnej.

• Wykorzystuje regułę delta do uczenia, aby zminimalizować błąd średniokwadratowy (MSE) między rzeczywistym wyjściem a pożądanym / docelowym wyjściem.

• Wagi i odchylenie są regulowane.

Architektura

Podstawowa struktura Adaline jest podobna do perceptronu mającego dodatkową pętlę sprzężenia zwrotnego, za pomocą której rzeczywisty sygnał wyjściowy jest porównywany z pożądanym / docelowym wyjściem. Po porównaniu na podstawie algorytmu uczącego wagi i odchylenie zostaną zaktualizowane.

Algorytm treningowy

Step 1 - Zainicjuj następujące elementy, aby rozpocząć szkolenie -

• Weights
• Bias
• Kurs nauki $ \ alpha $

W celu ułatwienia i uproszczenia obliczeń wagi i odchylenie należy ustawić na 0, a współczynnik uczenia się na 1.

Step 2 - Kontynuuj krok 3-8, jeśli warunek zatrzymania nie jest prawdziwy.

Step 3 - Kontynuuj krok 4-6 dla każdej dwubiegunowej pary treningowej s:t.

Step 4 - Aktywuj każdą jednostkę wejściową w następujący sposób -

$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: do \: n) $$

Step 5 - Uzyskaj dane wejściowe netto z następującą zależnością -

$$ y_ {in} \: = \: b \: + \: \ Displaystyle \ sum \ limity_ {i} ^ n x_ {i} \: w_ {i} $$

Tutaj ‘b’ jest stronniczość i ‘n’ to całkowita liczba neuronów wejściowych.

Step 6 - Zastosuj następującą funkcję aktywacji, aby uzyskać ostateczne wyjście -

$$ f (y_ {in}) \: = \: \ begin {cases} 1 & if \: y_ {in} \: \ geqslant \: 0 \\ - 1 & if \: y_ {in} \: < \: 0 \ end {cases} $$

Step 7 - Dostosuj wagę i odchylenie w następujący sposób -

Case 1 - jeśli y ≠ t następnie,

$$ w_ {i} (nowe) \: = \: w_ {i} (stare) \: + \: \ alpha (t \: - \: y_ {in}) x_ {i} $$

$$ b (nowe) \: = \: b (stare) \: + \: \ alpha (t \: - \: y_ {in}) $$

Case 2 - jeśli y = t następnie,

$$ w_ {i} (nowe) \: = \: w_ {i} (stare) $$

$$ b (nowy) \: = \: b (stary) $$

Tutaj ‘y’ to rzeczywista wydajność i ‘t’ jest pożądanym / docelowym wyjściem.

$ (t \: - \; y_ {in}) $ jest obliczonym błędem.

Step 8 - Test na stan zatrzymania, który nastąpi, gdy nie będzie zmiany wagi lub gdy wystąpiła największa zmiana wagi podczas treningu, jest mniejsza niż określona tolerancja.

Wiele adaptacyjnych neuronów liniowych (Madaline)

Madaline, co oznacza Multiple Adaptive Linear Neuron, to sieć, która składa się z wielu Adalines równolegle. Będzie miał jedną jednostkę wyjściową. Oto kilka ważnych punktów dotyczących Madaline -

• To jest jak wielowarstwowy perceptron, w którym Adaline będzie działać jako ukryta jednostka między wejściem a warstwą Madaline.

• Wagi i odchylenie między warstwami wejściowymi i Adaline, jak widać w architekturze Adaline, można regulować.

• Warstwy Adaline i Madaline mają ustaloną wagę i odchylenie równe 1.

• Trening można przeprowadzić za pomocą reguły Delta.

Architektura

Architektura Madaline składa się z “n” neurony warstwy wejściowej, “m”neurony warstwy Adaline i 1 neuron warstwy Madaline. Warstwę Adaline można uznać za warstwę ukrytą, ponieważ znajduje się między warstwą wejściową a warstwą wyjściową, tj. Warstwą Madaline.

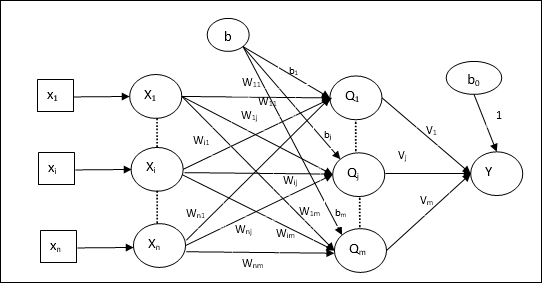
Algorytm treningowy

Do tej pory wiemy, że należy dopasować tylko wagi i odchylenie między wartością wejściową a warstwą Adaline, a wagi i odchylenie między warstwą Adaline i Madaline są stałe.

Step 1 - Zainicjuj następujące elementy, aby rozpocząć szkolenie -

• Weights
• Bias
• Kurs nauki $ \ alpha $

W celu ułatwienia i uproszczenia obliczeń wagi i odchylenie należy ustawić na 0, a współczynnik uczenia się na 1.

Step 2 - Kontynuuj krok 3-8, jeśli warunek zatrzymania nie jest prawdziwy.

Step 3 - Kontynuuj krok 4-6 dla każdej dwubiegunowej pary treningowej s:t.

Step 4 - Aktywuj każdą jednostkę wejściową w następujący sposób -

$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: do \: n) $$

Step 5 - Uzyskaj dane wejściowe netto w każdej ukrytej warstwie, tj. Warstwie Adaline z następującą relacją -

$$ Q_ {uszkodz} \: = \: b_ {j} \: + \: \ Displaystyle \ sum \ limity_ {i} ^ n x_ {i} \: w_ {ij} \: \: \: j \: = \: 1 \: do \: m $$

Tutaj ‘b’ jest stronniczość i ‘n’ to całkowita liczba neuronów wejściowych.

Step 6 - Zastosuj następującą funkcję aktywacji, aby uzyskać ostateczny efekt na warstwie Adaline i Madaline -

$$ f (x) \: = \: \ begin {cases} 1 & if \: x \: \ geqslant \: 0 \\ - 1 & if \: x \: <\: 0 \ end {cases} $ $

Wyjście na ukrytą (Adaline) jednostkę

$$ Q_ {j} \: = \: f (Q_ {inject}) $$

Końcowe wyjście sieci

$$ y \: = \: f (y_ {in}) $$

i.e. $ \: \: y_ {inject} \: = \: b_ {0} \: + \: \ sum_ {j = 1} ^ m \: Q_ {j} \: v_ {j} $

Step 7 - Obliczyć błąd i wyregulować wagi w następujący sposób -

Case 1 - jeśli y ≠ t i t = 1 następnie,

$$ w_ {ij} (nowy) \: = \: w_ {ij} (stary) \: + \: \ alpha (1 \: - \: Q_ {inject}) x_ {i} $$

$$ b_ {j} (nowe) \: = \: b_ {j} (stare) \: + \: \ alpha (1 \: - \: Q_ {inject}) $$

W takim przypadku wagi zostaną zaktualizowane Q_j gdzie wejście netto jest bliskie 0, ponieważ t = 1.

Case 2 - jeśli y ≠ t i t = -1 następnie,

$$ w_ {ik} (nowy) \: = \: w_ {ik} (stary) \: + \: \ alpha (-1 \: - \: Q_ {atrament}) x_ {i} $$

$$ b_ {k} (nowe) \: = \: b_ {k} (stare) \: + \: \ alpha (-1 \: - \: Q_ {atrament}) $$

W takim przypadku wagi zostaną zaktualizowane Q_k gdzie wkład netto jest dodatni, ponieważ t = -1.

Tutaj ‘y’ to rzeczywista wydajność i ‘t’ jest pożądanym / docelowym wyjściem.

Case 3 - jeśli y = t następnie

Nie byłoby żadnej zmiany wagi.

Step 8 - Test na stan zatrzymania, który nastąpi, gdy nie będzie zmiany wagi lub gdy wystąpiła największa zmiana wagi podczas treningu, jest mniejsza niż określona tolerancja.

Sieci neuronowe propagacji wstecznej

Back Propagation Neural (BPN) to wielowarstwowa sieć neuronowa składająca się z warstwy wejściowej, co najmniej jednej warstwy ukrytej i warstwy wyjściowej. Jak sama nazwa wskazuje, w tej sieci odbędzie się propagacja wsteczna. Błąd, który jest obliczany w warstwie wyjściowej, poprzez porównanie wyniku docelowego i rzeczywistego, będzie propagowany z powrotem w kierunku warstwy wejściowej.

Architektura

Jak pokazano na diagramie, architektura BPN ma trzy połączone ze sobą warstwy, na których znajdują się wagi. Warstwa ukryta, jak również warstwa wyjściowa, mają również odchylenie, którego waga wynosi zawsze 1. Jak wynika z diagramu, praca BPN przebiega w dwóch fazach. Jedna faza przesyła sygnał z warstwy wejściowej do warstwy wyjściowej, a druga faza z powrotem propaguje błąd z warstwy wyjściowej do warstwy wejściowej.

Algorytm treningowy

Do treningu BPN będzie używał binarnej funkcji aktywacji sigmoidy. Szkolenie BPN będzie miało następujące trzy fazy.

• Phase 1 - Faza posuwu naprzód

• Phase 2 - Powrót Propagacja błędu

• Phase 3 - Aktualizacja wag

Wszystkie te kroki zostaną zakończone w algorytmie w następujący sposób

Step 1 - Zainicjuj następujące elementy, aby rozpocząć szkolenie -

• Weights
• Kurs nauki $ \ alpha $

Aby ułatwić obliczenia i uprościć, weź kilka małych losowych wartości.

Step 2 - Kontynuuj krok 3-11, jeśli warunek zatrzymania nie jest prawdziwy.

Step 3 - Kontynuuj krok 4-10 dla każdej pary treningowej.

Faza 1

Step 4 - Każda jednostka wejściowa odbiera sygnał wejściowy x_i i wysyła go do ukrytej jednostki dla wszystkich i = 1 to n

Step 5 - Obliczyć wkład netto w ukrytej jednostce, korzystając z następującej zależności -

$$ Q_ {inject} \: = \: b_ {0j} \: + \: \ sum_ {i = 1} ^ n x_ {i} v_ {ij} \: \: \: \: j \: = \ : 1 \: do \: p $$

Tutaj b_0j jest stronniczość ukrytej jednostki, v_ij to waga j jednostka ukrytej warstwy pochodzącej z i jednostka warstwy wejściowej.

Teraz obliczyć moc wyjściową netto, stosując następującą funkcję aktywacji

$$ Q_ {j} \: = \: f (Q_ {inject}) $$

Wyślij te sygnały wyjściowe z ukrytych jednostek warstw do wyjściowych jednostek warstw.

Step 6 - Obliczyć wkład netto w jednostce warstwy wyjściowej przy użyciu następującej zależności -

$$ y_ {atrament} \: = \: b_ {0k} \: + \: \ sum_ {j = 1} ^ p \: Q_ {j} \: w_ {jk} \: \: k \: = \ : 1 \: do \: m $$

Tutaj b_0k ⁡Jest odchyleniem na jednostce wyjściowej, w_jk to waga k jednostka warstwy wyjściowej pochodzącej z j jednostka warstwy ukrytej.

Oblicz moc wyjściową netto, stosując następującą funkcję aktywacji

$$ y_ {k} \: = \: f (y_ {atrament}) $$

Faza 2

Step 7 - Obliczyć składnik korygujący błędy, zgodnie z wzorcem docelowym otrzymanym w każdej jednostce wyjściowej, w następujący sposób -

$$ \ delta_ {k} \: = \ :( t_ {k} \: - \: y_ {k}) f ^ {'} (y_ {atrament}) $$

Na tej podstawie zaktualizuj wagę i odchylenie w następujący sposób -

$$ \ Delta v_ {jk} \: = \: \ alpha \ delta_ {k} \: Q_ {ij} $$

$$ \ Delta b_ {0k} \: = \: \ alpha \ delta_ {k} $$

Następnie wyślij $ \ delta_ {k} $ z powrotem do ukrytej warstwy.

Step 8 - Teraz każda ukryta jednostka będzie sumą jej wartości delta z jednostek wyjściowych.

$$ \ delta_ {inject} \: = \: \ displaystyle \ sum \ limits_ {k = 1} ^ m \ delta_ {k} \: w_ {jk} $$

Termin błędu można obliczyć w następujący sposób -

$$ \ delta_ {j} \: = \: \ delta_ {inject} f ^ {'} (Q_ {inject}) $$

Na tej podstawie zaktualizuj wagę i odchylenie w następujący sposób -

$$ \ Delta w_ {ij} \: = \: \ alpha \ delta_ {j} x_ {i} $$

$$ \ Delta b_ {0j} \: = \: \ alpha \ delta_ {j} $$

Faza 3

Step 9 - Każda jednostka wyjściowa (y_kk = 1 to m) aktualizuje wagę i odchylenie w następujący sposób -

$$ v_ {jk} (nowe) \: = \: v_ {jk} (stare) \: + \: \ Delta v_ {jk} $$

$$ b_ {0k} (nowe) \: = \: b_ {0k} (stare) \: + \: \ Delta b_ {0k} $$

Step 10 - Każda jednostka wyjściowa (z_jj = 1 to p) aktualizuje wagę i odchylenie w następujący sposób -

$$ w_ {ij} (nowy) \: = \: w_ {ij} (stary) \: + \: \ Delta w_ {ij} $$

$$ b_ {0j} (nowe) \: = \: b_ {0j} (stare) \: + \: \ Delta b_ {0j} $$

Step 11 - Sprawdź stan zatrzymania, którym może być liczba osiągniętych epok lub docelowy wynik jest zgodny z rzeczywistym wyjściem.

Uogólniona reguła uczenia delta

Reguła delta działa tylko dla warstwy wyjściowej. Z drugiej strony uogólniona reguła delta, zwana również asback-propagation reguła, jest sposobem tworzenia pożądanych wartości warstwy ukrytej.

Sformułowanie matematyczne

Dla funkcji aktywacyjnej $ y_ {k} \: = \: f (y_ {atrament}) $ wyprowadzenie wkładu netto na warstwie ukrytej, jak również na warstwie wyjściowej można podać przez

$$ Y_ {atrament} \: = \: \ Displaystyle \ sum \ limits_i \: z_ {i} w_ {jk} $$

I $ \: \: y_ {inject} \: = \: \ sum_i x_ {i} v_ {ij} $

Teraz błąd, który należy zminimalizować, to

$$ E \: = \: \ Frac {1} {2} \ Displaystyle \ sum \ limits_ {k} \: [t_ {k} \: - \: y_ {k}] ^ 2 $$

Korzystając z reguły łańcucha, mamy

$$ \ Frac {\ częściowe E} {\ częściowe w_ {jk}} \: = \: \ Frac {\ częściowe} {\ częściowe w_ {jk}} (\ Frac {1} {2} \ displaystyle \ sum \ limity_ {k} \: [t_ {k} \: - \: y_ {k}] ^ 2) $$

$$ = \: \ frac {\ części} {\ częściowy w_ {jk}} \ lgroup \ frac {1} {2} [t_ {k} \: - \: t (y_ {atrament})] ^ 2 \ rgroup $$

$$ = \: - [t_ {k} \: - \: y_ {k}] \ frac {\ części} {\ częściowe w_ {jk}} f (y_ {atrament}) $$

$$ = \: - [t_ {k} \: - \: y_ {k}] f (y_ {atrament}) \ frac {\ częściowy} {\ częściowy w_ {jk}} (y_ {atrament}) $$

$$ = \: - [t_ {k} \: - \: y_ {k}] f ^ {'} (y_ {atrament}) z_ {j} $$

Teraz powiedzmy $ \ delta_ {k} \: = \: - [t_ {k} \: - \: y_ {k}] f ^ {'} (y_ {ink}) $

Wagi na połączeniach z ukrytą jednostką z_j może być udzielone przez -

$$ \ Frac {\ częściowe E} {\ częściowe v_ {ij}} \: = \: - \ Displaystyle \ suma \ limit_ {k} \ delta_ {k} \ frac {\ częściowe} {\ częściowe v_ {ij} } \ :( y_ {ink}) $$

Podając wartość $ y_ {ink} $ otrzymamy co następuje

$$ \ delta_ {j} \: = \: - \ displaystyle \ sum \ limits_ {k} \ delta_ {k} w_ {jk} f ^ {'} (z_ {uszkodz}) $$

Aktualizację wagi można przeprowadzić w następujący sposób -

Dla jednostki wyjściowej -

$$ \ Delta w_ {jk} \: = \: - \ alpha \ frac {\ częściowe E} {\ częściowe w_ {jk}} $$

$$ = \: \ alpha \: \ delta_ {k} \: z_ {j} $$

Za ukrytą jednostkę -

$$ \ Delta v_ {ij} \: = \: - \ alpha \ frac {\ częściowe E} {\ częściowe v_ {ij}} $$

$$ = \: \ alpha \: \ delta_ {j} \: x_ {i} $$

Jak sama nazwa wskazuje, ten rodzaj nauki odbywa się bez nadzoru nauczyciela. Ten proces uczenia się jest niezależny. Podczas uczenia SSN w ramach uczenia się bez nadzoru wektory wejściowe podobnego typu są łączone w klastry. Po zastosowaniu nowego wzorca wejściowego sieć neuronowa daje odpowiedź wyjściową wskazującą klasę, do której należy wzorzec wejściowy. W tym przypadku nie byłoby informacji zwrotnej ze środowiska, który powinien być pożądany i czy jest poprawny, czy nieprawidłowy. Stąd w tego typu uczeniu się sama sieć musi odkryć wzorce, cechy z danych wejściowych i relację danych wejściowych do danych wyjściowych.

Zwycięzca bierze wszystkie sieci

Tego rodzaju sieci opierają się na zasadzie konkurencyjnego uczenia się i wykorzystują strategię, w której jako zwycięzca wybiera neuron o największych łącznych nakładach. Połączenia między neuronami wyjściowymi pokazują, że konkurencja między nimi będzie „WŁĄCZONA”, co oznacza, że ​​będzie zwycięzcą, a inne będą „WYŁĄCZONE”.

Poniżej przedstawiono niektóre sieci oparte na tej prostej koncepcji wykorzystujące uczenie się bez nadzoru.

Sieć Hamminga

W większości sieci neuronowych wykorzystujących uczenie się bez nadzoru istotne jest obliczenie odległości i wykonywanie porównań. Ten rodzaj sieci to sieć Hamminga, w której dla każdego danego wektora wejściowego byłaby zgrupowana w różne grupy. Oto kilka ważnych funkcji sieci Hamminga -

• Lippmann rozpoczął pracę w sieciach Hamminga w 1987 roku.

• Jest to sieć jednowarstwowa.

• Wejścia mogą być binarne {0, 1} lub bipolarne {-1, 1}.

• Wagi sieci są obliczane przez przykładowe wektory.

• Jest to sieć o ustalonych obciążeniach, co oznacza, że ​​obciążenia pozostaną takie same nawet podczas treningu.

Max Net

Jest to również sieć o stałej wadze, która służy jako podsieć do wybierania węzła o najwyższym wejściu. Wszystkie węzły są w pełni ze sobą połączone, a we wszystkich tych ważonych połączeniach istnieją symetryczne wagi.

Architektura

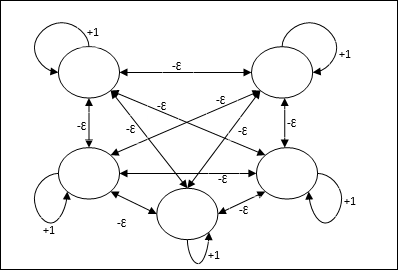
Wykorzystuje mechanizm, który jest procesem iteracyjnym, a każdy węzeł otrzymuje powstrzymujące dane wejściowe od wszystkich innych węzłów za pośrednictwem połączeń. Pojedynczy węzeł, którego wartość jest maksymalna, byłby aktywny lub zwycięski, a aktywacje wszystkich innych węzłów byłyby nieaktywne. Max Net używa funkcji aktywacji tożsamości z $$ f (x) \: = \: \ begin {cases} x & if \: x> 0 \\ 0 & if \: x \ leq 0 \ end {cases} $$

Zadanie tej sieci jest realizowane przez wagę samowzbudzenia równą +1 i wielkość wzajemnego hamowania, która jest ustawiona jako [0 <ɛ <$ \ frac {1} {m} $] gdzie “m” to całkowita liczba węzłów.

Konkurencyjne uczenie się w ANN

Dotyczy to nienadzorowanego szkolenia, w którym węzły wyjściowe próbują ze sobą konkurować, aby reprezentować wzorzec wejściowy. Aby zrozumieć tę zasadę uczenia się, będziemy musieli zrozumieć sieć konkurencyjną, która jest wyjaśniona w następujący sposób:

Podstawowa koncepcja sieci konkurencji

Ta sieć jest jak jednowarstwowa sieć sprzężenia zwrotnego z połączeniem zwrotnym między wyjściami. Połączenia między wyjściami są typu hamującego, co zaznaczono liniami przerywanymi, co oznacza, że ​​zawodnicy nigdy się nie utrzymują.

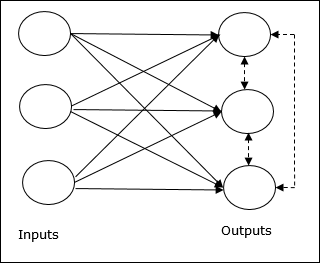
Podstawowa koncepcja reguły konkurencyjnej nauki

Jak wspomniano wcześniej, między węzłami wyjściowymi wystąpiłaby konkurencja, więc główna koncepcja jest taka - podczas treningu jednostka wyjściowa, która ma największą aktywację dla danego wzorca wejściowego, zostanie ogłoszona zwycięzcą. Ta zasada jest również nazywana zwycięzcą bierze wszystko, ponieważ tylko zwycięski neuron jest aktualizowany, a reszta neuronów pozostaje niezmieniona.

Sformułowanie matematyczne

Poniżej przedstawiono trzy ważne czynniki, które wpływają na matematyczne sformułowanie tej zasady uczenia się:

• Warunek zwycięstwa

  Załóżmy, że neuron y_k chce być zwycięzcą, to byłby następujący warunek

  $$ y_ {k} \: = \: \ begin {cases} 1 & if \: v_ {k}> v_ {j} \: for \: all \: \: j, \: j \: \ neq \ : k \\ 0 & poza tym \ end {cases} $$

  Oznacza to, że jeśli jakikolwiek neuron, powiedzmy, y_k chce wygrać, a następnie, powiedzmy, jego indukowane pole lokalne (wyjście jednostki sumującej) v_k, musi być największym spośród wszystkich innych neuronów w sieci.

• Stan sumy masy całkowitej

  Innym ograniczeniem reguły konkurencyjnego uczenia się jest suma wag dla konkretnego neuronu wyjściowego, która wyniesie 1. Na przykład, jeśli rozważymy neuron k następnie

  $$ \ Displaystyle \ sum \ limity_ {k} w_ {kj} \: = \: 1 \: \: \: \: dla \: all \: \: k $$

• Zmiana wagi dla zwycięzcy

  Jeśli neuron nie reaguje na wzorzec wejściowy, to w tym neuronie nie ma miejsca uczenie się. Jeśli jednak wygrywa dany neuron, odpowiednie wagi są korygowane w następujący sposób -

  $$ \ Delta w_ {kj} \: = \: \ begin {cases} - \ alpha (x_ {j} \: - \: w_ {kj}), & if \: neuron \: k \: wins \\ 0 & if \: neuron \: k \: loss \ end {cases} $$

  Tutaj $ \ alpha $ to współczynnik uczenia się.

  To wyraźnie pokazuje, że faworyzujemy zwycięski neuron, dostosowując jego wagę, a jeśli neuron zostanie zgubiony, nie musimy przejmować się ponownym dostosowywaniem jego wagi.

Algorytm grupowania środków K-średnich

K-średnie to jeden z najpopularniejszych algorytmów klastrowania, w którym wykorzystujemy koncepcję procedury partycjonowania. Rozpoczynamy od wstępnej partycji i wielokrotnie przenosimy wzorce z jednego klastra do drugiego, aż uzyskamy satysfakcjonujący wynik.

Algorytm

Step 1 - Wybierz kpunkty jako początkowe centroidy. Zainicjujk prototypy (w₁,…,w_k), na przykład możemy je zidentyfikować za pomocą losowo wybranych wektorów wejściowych -

$$ W_ {j} \: = \: i_ {p}, \: \: \: gdzie \: j \: \ in \ lbrace1, ...., k \ rbrace \: and \: p \: \ w \ lbrace1, ...., n \ rbrace $$

Każdy klaster C_j jest związany z prototypem w_j.

Step 2 - Powtarzaj krok 3-5, aż E przestanie maleć lub członkostwo w klastrze przestanie się zmieniać.

Step 3 - Dla każdego wektora wejściowego i_p gdzie p ∈ {1,…,n}, położyć i_p w klastrze C_j* z najbliższym prototypem w_j* mający następujący związek

$$ | i_ {p} \: - \: w_ {j *} | \: \ leq \: | i_ {p} \: - \: w_ {j} |, \: j \: \ in \ lbrace1, ...., k \ rbrace $$

Step 4 - Dla każdego klastra C_j, gdzie j ∈ { 1,…,k}zaktualizuj prototyp w_j być centroidem wszystkich próbek, które są obecnie w C_j więc to

$$ w_ {j} \: = \: \ sum_ {i_ {p} \ in C_ {j}} \ frac {i_ {p}} {| C_ {j} |} $$

Step 5 - Obliczyć całkowity błąd kwantyzacji w następujący sposób -

$$ E \: = \: \ sum_ {j = 1} ^ k \ sum_ {i_ {p} \ in w_ {j}} | i_ {p} \: - \: w_ {j} | ^ 2 $$

Neocognitron

Jest to wielowarstwowa sieć sprzężenia zwrotnego, która została opracowana przez Fukushimę w latach 80. Model ten jest oparty na uczeniu nadzorowanym i służy do wizualnego rozpoznawania wzorców, głównie znaków pisanych ręcznie. Jest to w zasadzie rozszerzenie sieci Cognitron, która została również opracowana przez Fukushimę w 1975 roku.

Architektura

Jest to sieć hierarchiczna, która składa się z wielu warstw i lokalnie w tych warstwach istnieje wzorzec połączeń.

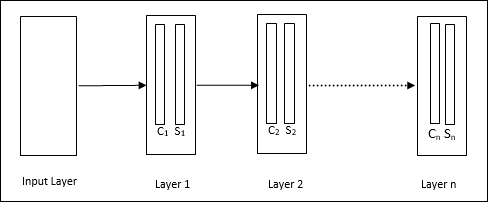
Jak widzieliśmy na powyższym diagramie, neokognitron jest podzielony na różne połączone ze sobą warstwy, a każda warstwa ma dwie komórki. Wyjaśnienie tych komórek jest następujące -

S-Cell - Nazywa się to prostą komórką, która jest trenowana, aby reagować na określony wzór lub grupę wzorców.

C-Cell- Nazywa się to komórką złożoną, która łączy dane wyjściowe z komórki S i jednocześnie zmniejsza liczbę jednostek w każdej tablicy. W innym sensie komórka C zastępuje wynik komórki S.

Algorytm treningowy

Stwierdzono, że trening neokognitronu postępuje warstwa po warstwie. Wagi z warstwy wejściowej do pierwszej warstwy są trenowane i zamrażane. Następnie trenowane są ciężary od pierwszej do drugiej warstwy i tak dalej. Wewnętrzne obliczenia między komórką S i komórką C zależą od wag pochodzących z poprzednich warstw. Dlatego możemy powiedzieć, że algorytm uczący zależy od obliczeń na komórkach S i C.

Obliczenia w komórce S.

Komórka S posiada sygnał pobudzający otrzymany z poprzedniej warstwy i posiada sygnały hamujące otrzymane w tej samej warstwie.

$$ \ theta = \: \ sqrt {\ sum \ sum t_ {i} c_ {i} ^ 2} $$

Tutaj, t_i to stała waga i c_i jest wyjściem z komórki C.

Skalowane dane wejściowe komórki S można obliczyć w następujący sposób -

$$ x \: = \: \ frac {1 \: + \: e} {1 \: + \: vw_ {0}} \: - \: 1 $$

Tutaj $ e \: = \: \ sum_i c_ {i} w_ {i} $

w_i jest wagą skorygowaną z ogniwa C do ogniwa S.

w₀ to waga regulowana pomiędzy wejściem a ogniwem S.

v jest pobudzającym wejściem z komórki C.

Aktywacja sygnału wyjściowego to:

$$ s \: = \: \ begin {cases} x, & if \: x \ geq 0 \\ 0, & if \: x <0 \ end {cases} $$

Obliczenia w komórce C.

Wkład netto warstwy C wynosi

$$ C \: = \: \ Displaystyle \ sum \ limits_i s_ {i} x_ {i} $$

Tutaj, s_i jest wyjściem z komórki S i x_i jest stałą wagą z ogniwa S do ogniwa C.

Ostateczny wynik jest następujący -

$$ C_ {out} \: = \: \ begin {cases} \ frac {C} {a + C}, & if \: C> 0 \\ 0, & w przeciwnym razie \ end {cases} $$

Tutaj ‘a’ to parametr, który zależy od wydajności sieci.

Uczenie się kwantyzacji wektorów (LVQ), różni się od kwantyzacji wektorów (VQ) i map samoorganizujących się Kohonena (KSOM), jest w zasadzie konkurencyjną siecią, która wykorzystuje nadzorowane uczenie się. Możemy zdefiniować to jako proces klasyfikowania wzorców, w których każda jednostka wyjściowa reprezentuje klasę. Ponieważ wykorzystuje uczenie nadzorowane, sieć otrzyma zestaw wzorców uczących ze znaną klasyfikacją wraz z początkową dystrybucją klasy wyjściowej. Po zakończeniu procesu uczenia LVQ sklasyfikuje wektor wejściowy, przypisując go do tej samej klasy, co jednostka wyjściowa.

Architektura

Poniższy rysunek przedstawia architekturę LVQ, która jest dość podobna do architektury KSOM. Jak widzimy, są“n” liczba jednostek wejściowych i “m”liczba jednostek wyjściowych. Warstwy są w pełni połączone ze sobą i mają na sobie ciężarki.

Używane parametry

Poniżej przedstawiono parametry używane w procesie uczenia LVQ, a także w schemacie blokowym

• x= wektor uczący (x ₁ , ..., x _i , ..., x _n )

• T = klasa dla wektora szkoleniowego x

• w_j = wektor wagi dla j^th jednostka wyjściowa

• C_j = klasa skojarzona z j^th jednostka wyjściowa

Algorytm treningowy

Step 1 - Zainicjuj wektory odniesienia, co można zrobić w następujący sposób -

• Step 1(a) - Z podanego zestawu wektorów uczących weź pierwszy „m”(Liczba klastrów) wektorów uczących i używaj ich jako wektorów wagi. Pozostałe wektory można wykorzystać do treningu.

• Step 1(b) - Losowo przypisz wagę początkową i klasyfikację.

• Step 1(c) - Zastosuj metodę grupowania średnich wartości K.

Step 2 - Zainicjuj wektor odniesienia $ \ alpha $

Step 3 - Kontynuuj kroki 4-9, jeśli warunek zatrzymania tego algorytmu nie jest spełniony.

Step 4 - Wykonaj kroki 5-6 dla każdego wektora wejściowego szkolenia x.

Step 5 - Oblicz kwadrat odległości euklidesowej dla j = 1 to m i i = 1 to n

$$ D (j) \: = \: \ Displaystyle \ suma \ limit_ {i = 1} ^ n \ Displaystyle \ suma \ limity_ {j = 1} ^ m (x_ {i} \: - \: w_ {ij }) ^ 2 $$

Step 6 - Zdobądź zwycięską jednostkę J gdzie D(j) jest minimum.

Step 7 - Oblicz nową wagę zwycięskiej jednostki za pomocą następującej zależności -

Jeśli T = C_j następnie $ w_ {j} (nowy) \: = \: w_ {j} (stary) \: + \: \ alpha [x \: - \: w_ {j} (stary)] $

Jeśli T ≠ C_j następnie $ w_ {j} (nowy) \: = \: w_ {j} (stary) \: - \: \ alpha [x \: - \: w_ {j} (stary)] $

Step 8 - Zmniejsz współczynnik uczenia się $ \ alpha $.

Step 9- Sprawdź stan zatrzymania. Może wyglądać następująco -

• Osiągnięto maksymalną liczbę epok.
• Szybkość uczenia się zredukowana do znikomej wartości.

Schemat blokowy

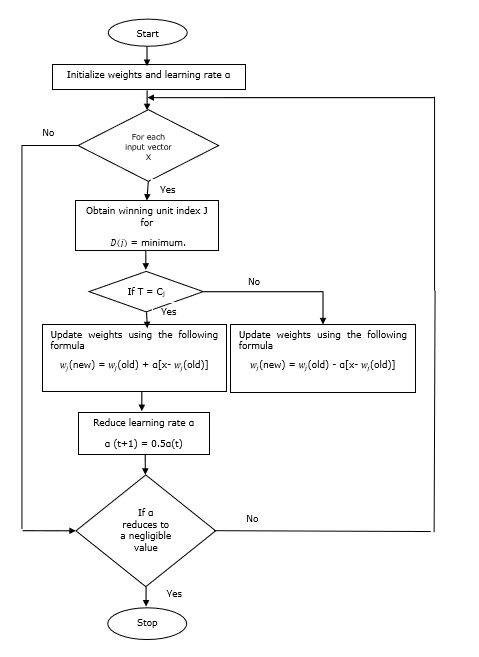
Warianty

Trzy inne warianty, a mianowicie LVQ2, LVQ2.1 i LVQ3, zostały opracowane przez Kohonena. Złożoność we wszystkich tych trzech wariantach, ze względu na koncepcję, której nauczy się zwycięzca i druga jednostka, jest większa niż w LVQ.

LVQ2

Jak omówiono, koncepcja innych wariantów LVQ powyżej, stan LVQ2 jest tworzony przez okno. To okno będzie oparte na następujących parametrach -

• x - aktualny wektor wejściowy

• y_c - wektor odniesienia najbliższy x

• y_r - inny wektor odniesienia, który jest następny najbliżej x

• d_c - odległość od x do y_c

• d_r - odległość od x do y_r

Wektor wejściowy x wpadnie w okno, jeśli

$$ \ frac {d_ {c}} {d_ {r}} \:> \: 1 \: - \: \ theta \: \: i \: \: \ frac {d_ {r}} {d_ {c }} \:> \: 1 \: + \: \ theta $$

Tutaj $ \ theta $ to liczba próbek treningowych.

Aktualizację można przeprowadzić za pomocą następującego wzoru -

$ y_ {c} (t \: + \: 1) \: = \: y_ {c} (t) \: + \: \ alpha (t) [x (t) \: - \: y_ {c} (t)] $ (belongs to different class)

$ y_ {r} (t \: + \: 1) \: = \: y_ {r} (t) \: + \: \ alpha (t) [x (t) \: - \: y_ {r} (t)] $ (belongs to same class)

Tutaj $ \ alpha $ to współczynnik uczenia się.

LVQ2.1

W LVQ2.1 weźmiemy dwa najbliższe wektory, a mianowicie y_c1 i y_c2 a stan okna jest następujący -

$$ Min \ begin {bmatrix} \ frac {d_ {c1}} {d_ {c2}}, \ frac {d_ {c2}} {d_ {c1}} \ end {bmatrix} \:> \ :( 1 \ : - \: \ theta) $$

$$ Max \ begin {bmatrix} \ frac {d_ {c1}} {d_ {c2}}, \ frac {d_ {c2}} {d_ {c1}} \ end {bmatrix} \: <\ :( 1 \ : + \: \ theta) $$

Aktualizację można przeprowadzić za pomocą następującego wzoru -

$ y_ {c1} (t \: + \: 1) \: = \: y_ {c1} (t) \: + \: \ alpha (t) [x (t) \: - \: y_ {c1} (t)] $ (belongs to different class)

$ y_ {c2} (t \: + \: 1) \: = \: y_ {c2} (t) \: + \: \ alpha (t) [x (t) \: - \: y_ {c2} (t)] $ (belongs to same class)

Tutaj $ \ alpha $ to współczynnik uczenia się.

LVQ3

W LVQ3 weźmiemy dwa najbliższe wektory, a mianowicie y_c1 i y_c2 a stan okna jest następujący -

$$ Min \ begin {bmatrix} \ frac {d_ {c1}} {d_ {c2}}, \ frac {d_ {c2}} {d_ {c1}} \ end {bmatrix} \:> \ :( 1 \ : - \: \ theta) (1 \: + \: \ theta) $$

Tutaj $ \ theta \ około 0,2 $

Aktualizację można przeprowadzić za pomocą następującego wzoru -

$ y_ {c1} (t \: + \: 1) \: = \: y_ {c1} (t) \: + \: \ beta (t) [x (t) \: - \: y_ {c1} (t)] $ (belongs to different class)

$ y_ {c2} (t \: + \: 1) \: = \: y_ {c2} (t) \: + \: \ beta (t) [x (t) \: - \: y_ {c2} (t)] $ (belongs to same class)

Tutaj $ \ beta $ jest wielokrotnością współczynnika uczenia się $ \ alpha $ i $\beta\:=\:m \alpha(t)$ dla każdego 0.1 < m < 0.5

Sieć ta została stworzona przez Stephena Grossberga i Gail Carpenter w 1987 roku. Opiera się na konkurencji i wykorzystuje model uczenia się bez nadzoru. Sieci Adaptive Resonance Theory (ART), jak sama nazwa wskazuje, są zawsze otwarte na nowe uczenie się (adaptacyjne) bez utraty starych wzorców (rezonans). Zasadniczo sieć ART jest klasyfikatorem wektorów, który akceptuje wektor wejściowy i klasyfikuje go do jednej z kategorii w zależności od tego, który z przechowywanych wzorców najbardziej przypomina.

Dyrektor operacyjny

Główną operację klasyfikacji ART można podzielić na następujące fazy -

• Recognition phase- Wektor wejściowy jest porównywany z klasyfikacją przedstawioną w każdym węźle warstwy wyjściowej. Sygnał wyjściowy neuronu przyjmuje wartość „1”, jeśli najlepiej pasuje do zastosowanej klasyfikacji, w przeciwnym razie przyjmuje wartość „0”.

• Comparison phase- W tej fazie wykonywane jest porównanie wektora wejściowego z wektorem warstwy porównawczej. Warunkiem zresetowania jest, aby stopień podobieństwa był mniejszy niż parametr czujności.

• Search phase- W tej fazie sieć wyszuka reset, a także dopasowanie wykonane w powyższych fazach. Stąd, jeśli nie byłoby resetu i mecz jest całkiem dobry, to klasyfikacja się kończy. W przeciwnym razie proces zostałby powtórzony, a inny zapisany wzorzec musiałby zostać wysłany, aby znaleźć prawidłowe dopasowanie.

ART1

Jest to rodzaj ART, który jest przeznaczony do grupowania wektorów binarnych. Możemy to zrozumieć dzięki jego architekturze.

Architektura ART1

Składa się z następujących dwóch jednostek -

Computational Unit - Składa się z następujących -

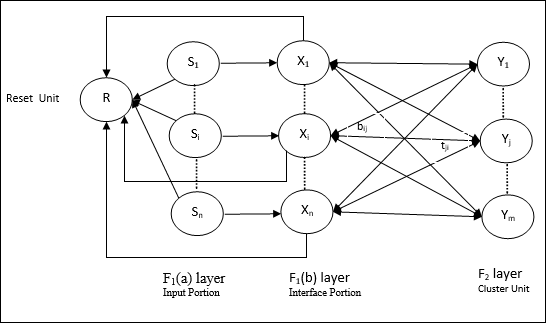
• Input unit (F₁ layer) - Ponadto ma następujące dwie porcje -

  • F₁(a) layer (Input portion)- W ART1 nie byłoby przetwarzania w tej części, zamiast mieć tylko wektory wejściowe. Jest on połączony z F ₁ (B), warstwa (część Interface).

  • F₁(b) layer (Interface portion)- Ta część łączy sygnał z części wejściowej z sygnałem warstwy F ₂ . Warstwa F ₁ (b) jest połączona z warstwą F ₂ ciężarkami od dołu do góryb_iji F ₂ warstwa jest połączona F ₁ (b) z góry na dół warstwy wagt_ji.

• Cluster Unit (F₂ layer)- To jest warstwa konkurencyjna. Do nauki wzorca wejściowego wybierana jest jednostka o największej wartości wejściowej netto. Aktywacja wszystkich innych jednostek klastra jest ustawiona na 0.

• Reset Mechanism- Działanie tego mechanizmu opiera się na podobieństwie między wagą odgórną a wektorem wejściowym. Otóż, jeśli stopień tego podobieństwa jest mniejszy niż parametr czujności, wówczas klaster nie może nauczyć się wzorca i nastąpi odpoczynek.

Supplement Unit - Właściwie problem z mechanizmem resetowania polega na tym, że warstwa F₂muszą być hamowane pod pewnymi warunkami i muszą być również dostępne, gdy ma miejsce nauka. Dlatego dwie dodatkowe jednostki, a mianowicie:G₁ i G₂ jest dodawany wraz z resetem jednostki, R. Nazywają sięgain control units. Jednostki te odbierają i wysyłają sygnały do ​​innych jednostek obecnych w sieci.‘+’ wskazuje sygnał pobudzający, podczas gdy ‘−’ wskazuje na sygnał hamujący.

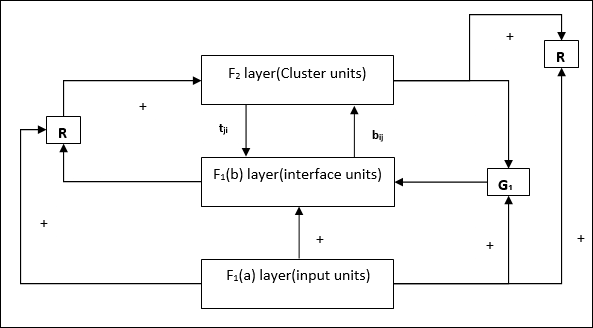
Używane parametry

Używane są następujące parametry -

• n - Liczba elementów w wektorze wejściowym

• m - Maksymalna liczba klastrów, które można utworzyć

• b_ij- Waga od warstwy F ₁ (b) do F ₂ , tj. Wagi oddolne

• t_ji- Waga od warstwy F ₂ do F ₁ (b), czyli ciężary odgórne

• ρ - parametr czujności

• ||x|| - Norma wektora x

Algorytm

Step 1 - Zainicjuj szybkość uczenia się, parametr czujności i wagi w następujący sposób -

$$ \ alpha \:> \: 1 \: \: i \: \: 0 \: <\ rho \: \ leq \: 1 $$

$$ 0 \: <\: b_ {ij} (0) \: <\: \ frac {\ alpha} {\ alpha \: - \: 1 \: + \: n} \: \: i \: \: t_ {ij} (0) \: = \: 1 $$

Step 2 - Kontynuuj krok 3-9, jeśli warunek zatrzymania nie jest spełniony.

Step 3 - Kontynuuj krok 4-6 dla każdego wejścia treningowego.

Step 4- Ustaw aktywacje wszystkich jednostek F ₁ (a) i F ₁ w następujący sposób

F₂ = 0 and F₁(a) = input vectors

Step 5- Sygnał wejściowy z warstwy F ₁ (a) do F ₁ (b) musi być przesłany jak

$$ s_ {i} \: = \: x_ {i} $$

Step 6- Dla każdego zablokowanego węzła F ₂

$ y_ {j} \: = \: \ sum_i b_ {ij} x_ {i} $ warunkiem jest y_j ≠ -1

Step 7 - Wykonaj kroki 8-10, gdy reset jest prawdziwy.

Step 8 - Znajdź J dla y_J ≥ y_j dla wszystkich węzłów j

Step 9- Ponownie obliczyć aktywację na F ₁ (b) w następujący sposób

$$ x_ {i} \: = \: sitJi $$

Step 10 - Teraz, po obliczeniu normy wektora x i wektor smusimy sprawdzić stan resetowania w następujący sposób -

Jeśli ||x||/ ||s|| <parametr czujności ρ, ⁡Then⁡inhibit ⁡node J i przejdź do kroku 7

Inaczej, jeśli ||x||/ ||s|| ≥ parametr czujności ρ, a następnie przejdź dalej.

Step 11 - Aktualizacja wagi dla węzła J można zrobić w następujący sposób -

$$ b_ {ij} (nowy) \: = \: \ frac {\ alpha x_ {i}} {\ alpha \: - \: 1 \: + \: || x ||} $$

$$ t_ {ij} (nowy) \: = \: x_ {i} $$

Step 12 - Warunek zatrzymania algorytmu musi zostać sprawdzony i może wyglądać następująco -

• Nie mają żadnej zmiany wagi.
• Reset nie jest wykonywany dla jednostek.
• Osiągnięto maksymalną liczbę epok.

Załóżmy, że mamy jakiś wzór dowolnych wymiarów, jednak potrzebujemy ich w jednym lub dwóch wymiarach. Wtedy proces mapowania cech byłby bardzo przydatny do przekształcenia szerokiej przestrzeni wzorców w typową przestrzeń cech. Teraz pojawia się pytanie, dlaczego potrzebujemy samoorganizującej się mapy cech? Powodem jest to, że oprócz możliwości konwersji dowolnych wymiarów na 1-D lub 2-D, musi również mieć możliwość zachowania sąsiedniej topologii.

Sąsiednie topologie w Kohonen SOM

Mogą istnieć różne topologie, jednak najczęściej używane są dwie następujące topologie -

Prostokątna topologia siatki

Ta topologia ma 24 węzły w siatce odległość-2, 16 węzłów w siatce odległość-1 i 8 węzłów w siatce odległość-0, co oznacza, że ​​różnica między każdą siatką prostokątną wynosi 8 węzłów. Zwycięska jednostka jest oznaczona przez #.

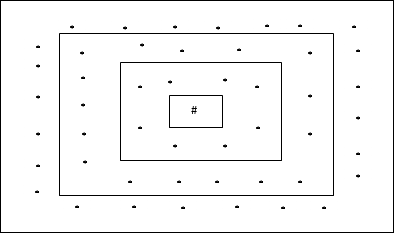
Sześciokątna topologia siatki

Ta topologia ma 18 węzłów w siatce odległość-2, 12 węzłów w siatce odległość-1 i 6 węzłów w siatce odległość-0, co oznacza, że ​​różnica między każdą siatką prostokątną wynosi 6 węzłów. Zwycięska jednostka jest oznaczona przez #.

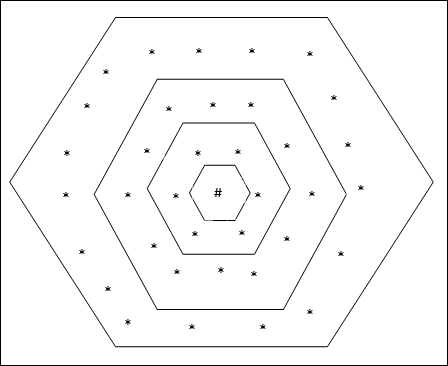
Architektura

Architektura KSOM jest podobna do architektury konkurencyjnej sieci. Za pomocą omówionych wcześniej schematów sąsiedzkich szkolenie może odbywać się w rozszerzonym regionie sieci.

Algorytm do treningu

Step 1 - Zainicjuj wagi, tempo uczenia się α i schemat topologii sąsiedztwa.

Step 2 - Kontynuuj krok 3-9, jeśli warunek zatrzymania nie jest spełniony.

Step 3 - Kontynuuj krok 4-6 dla każdego wektora wejściowego x.

Step 4 - Oblicz kwadrat odległości euklidesowej dla j = 1 to m

$$ D (j) \: = \: \ Displaystyle \ suma \ limity_ {i = 1} ^ n \ Displaystyle \ suma \ limity_ {j = 1} ^ m (x_ {i} \: - \: w_ {ij }) ^ 2 $$

Step 5 - Zdobądź zwycięską jednostkę J gdzie D(j) jest minimum.

Step 6 - Oblicz nową wagę zwycięskiej jednostki za pomocą następującej zależności -

$$ w_ {ij} (nowy) \: = \: w_ {ij} (stary) \: + \: \ alpha [x_ {i} \: - \: w_ {ij} (stary)] $$

Step 7 - Zaktualizuj współczynnik uczenia się α przez następującą relację -

$$ \ alpha (t \: + \: 1) \: = \: 0.5 \ alpha t $$

Step 8 - Zmniejsz promień schematu topologicznego.

Step 9 - Sprawdź stan zatrzymania sieci.

Tego rodzaju sieci neuronowe działają na zasadzie asocjacji wzorców, co oznacza, że ​​mogą przechowywać różne wzorce, aw momencie wydawania danych wyjściowych mogą wytworzyć jeden z przechowywanych wzorców, dopasowując je do danego wzorca wejściowego. Tego typu wspomnienia są również nazywaneContent-Addressable Memory(KRZYWKA). Pamięć asocjacyjna przeprowadza równoległe wyszukiwanie z zapisanymi wzorcami jako plikami danych.

Poniżej przedstawiono dwa typy wspomnień asocjacyjnych, które możemy zaobserwować -

• Pamięć autoasocjacyjna
• Pamięć asocjacyjna hetero

Pamięć autoasocjacyjna

Jest to jednowarstwowa sieć neuronowa, w której wejściowy wektor szkoleniowy i wyjściowy wektor docelowy są takie same. Wagi są określane tak, aby sieć przechowała zestaw wzorców.

Architektura

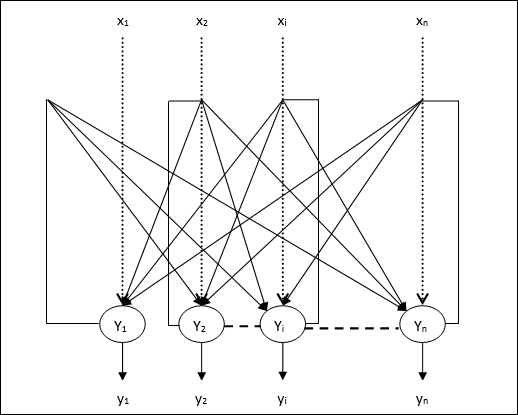
Jak pokazano na poniższym rysunku, architektura sieci pamięci Auto Associative ma ‘n’ liczba wejściowych wektorów uczących i podobnych ‘n’ liczba wyjściowych wektorów docelowych.

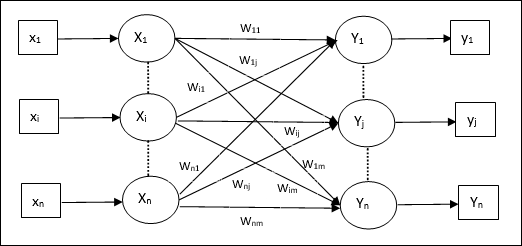
Algorytm treningowy

Na potrzeby szkolenia ta sieć korzysta z reguły uczenia się Hebb lub Delta.

Step 1 - Zainicjuj wszystkie wagi do zera jako w_ij = 0 (i = 1 to n, j = 1 to n)

Step 2 - Wykonaj kroki 3-4 dla każdego wektora wejściowego.

Step 3 - Aktywuj każdą jednostkę wejściową w następujący sposób -

$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: do \: n) $$

Step 4 - Aktywuj każdą jednostkę wyjściową w następujący sposób -

$$ y_ {j} \: = \: s_ {j} \ :( j \: = \: 1 \: do \: n) $$

Step 5 - Wyreguluj ciężary w następujący sposób -

$$ w_ {ij} (nowe) \: = \: w_ {ij} (stare) \: + \: x_ {i} y_ {j} $$

Algorytm testowania

Step 1 - Ustaw wagi uzyskane podczas treningu dla reguły Hebba.

Step 2 - Wykonaj kroki 3-5 dla każdego wektora wejściowego.

Step 3 - Ustaw aktywację jednostek wejściowych równą tej z wektora wejściowego.

Step 4 - Oblicz wkład netto dla każdej jednostki wyjściowej j = 1 to n

$$ y_ {uszkodzenie} \: = \: \ Displaystyle \ suma \ limits_ {i = 1} ^ n x_ {i} w_ {ij} $$

Step 5 - Zastosuj następującą funkcję aktywacji, aby obliczyć moc

$$ y_ {j} \: = \: f (y_ {inject}) \: = \: \ begin {cases} +1 & if \: y_ {inject} \:> \: 0 \\ - 1 & if \: y_ {inject} \: \ leqslant \: 0 \ end {cases} $$

Pamięć asocjacyjna hetero

Podobnie jak w przypadku sieci Auto Associative Memory, jest to również jednowarstwowa sieć neuronowa. Jednak w tej sieci wejściowy wektor uczący i wyjściowy wektor docelowy nie są takie same. Wagi są określane tak, aby sieć przechowała zestaw wzorców. Sieć hetero asocjacyjna ma charakter statyczny, dlatego nie byłoby operacji nieliniowych i opóźniających.

Architektura

Jak pokazano na poniższym rysunku, architektura sieci Hetero Associative Memory ma ‘n’ liczba wejściowych wektorów uczących i ‘m’ liczba wyjściowych wektorów docelowych.

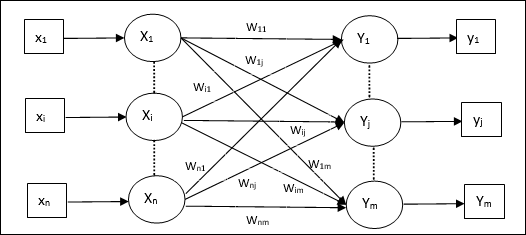
Algorytm treningowy

Na potrzeby szkolenia ta sieć korzysta z reguły uczenia się Hebb lub Delta.

Step 1 - Zainicjuj wszystkie wagi do zera jako w_ij = 0 (i = 1 to n, j = 1 to m)

Step 2 - Wykonaj kroki 3-4 dla każdego wektora wejściowego.

Step 3 - Aktywuj każdą jednostkę wejściową w następujący sposób -

$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: do \: n) $$

Step 4 - Aktywuj każdą jednostkę wyjściową w następujący sposób -

$$ y_ {j} \: = \: s_ {j} \ :( j \: = \: 1 \: do \: m) $$

Step 5 - Wyreguluj ciężary w następujący sposób -

$$ w_ {ij} (nowe) \: = \: w_ {ij} (stare) \: + \: x_ {i} y_ {j} $$

Algorytm testowania

Step 1 - Ustaw wagi uzyskane podczas treningu dla reguły Hebba.

Step 2 - Wykonaj kroki 3-5 dla każdego wektora wejściowego.

Step 3 - Ustaw aktywację jednostek wejściowych równą tej z wektora wejściowego.

Step 4 - Oblicz wkład netto dla każdej jednostki wyjściowej j = 1 to m;

$$ y_ {uszkodzenie} \: = \: \ Displaystyle \ suma \ limits_ {i = 1} ^ n x_ {i} w_ {ij} $$

Step 5 - Zastosuj następującą funkcję aktywacji, aby obliczyć moc

$$ y_ {j} \: = \: f (y_ {inject}) \: = \: \ begin {cases} +1 & if \: y_ {inject} \:> \: 0 \\ 0 & if \ : y_ {inject} \: = \: 0 \\ - 1 & if \: y_ {inject} \: <\: 0 \ end {cases} $$

Sieć neuronowa Hopfield została wynaleziona przez dr. Johna J. Hopfielda w 1982 r. Składa się z pojedynczej warstwy zawierającej jeden lub więcej w pełni połączonych neuronów nawracających. Sieć Hopfield jest powszechnie używana do zadań auto-asocjacji i optymalizacji.

Dyskretna Sieć Hopfielda

Sieć Hopfielda, która działa w sposób dyskretny lub innymi słowy, można powiedzieć, że wzorce wejściowe i wyjściowe są dyskretnymi wektorami, które mogą mieć charakter binarny (0,1) lub bipolarny (+1, -1). Sieć ma symetryczne wagi bez połączeń samoczynnych tj.w_ij = w_ji i w_ii = 0.

Architektura

Oto kilka ważnych punktów, o których należy pamiętać w przypadku dyskretnej sieci Hopfield:

• Model ten składa się z neuronów z jednym wyjściem odwracającym i jednym nieodwracającym.

• Sygnałem wyjściowym każdego neuronu powinno być wejście innych neuronów, ale nie wejście samego siebie.

• Waga / siła połączenia jest reprezentowana przez w_ij.

• Połączenia mogą być zarówno pobudzające, jak i hamujące. Byłoby pobudzające, gdyby sygnał wyjściowy neuronu był taki sam jak wejście, w przeciwnym razie hamowałby.

• Wagi powinny być symetryczne, tj w_ij = w_ji

Dane wyjściowe z Y₁ zamierzam Y₂, Y_i i Y_n mieć ciężary w₁₂, w_1i i w_1nodpowiednio. Podobnie, inne łuki mają na sobie ciężary.

Algorytm treningowy

Podczas treningu dyskretnej sieci Hopfield wagi będą aktualizowane. Jak wiemy, możemy mieć binarne wektory wejściowe, a także bipolarne wektory wejściowe. W związku z tym w obu przypadkach aktualizacje wagi można przeprowadzić za pomocą następującej relacji

Case 1 - Wzorce wejść binarnych

Zestaw wzorców binarnych s(p), p = 1 to P

Tutaj, s(p) = s₁(p), s₂(p),..., s_i(p),..., s_n(p)

Macierz wagi jest podana przez

$$ w_ {ij} \: = \: \ sum_ {p = 1} ^ P [2s_ {i} (p) - \: 1] [2s_ {j} (p) - \: 1] \: \: \: \: \: dla \: i \: \ neq \: j $$

Case 2 - Bipolarne wzorce wejściowe

Zestaw wzorców binarnych s(p), p = 1 to P

Tutaj, s(p) = s₁(p), s₂(p),..., s_i(p),..., s_n(p)

Macierz wagi jest podana przez

$$ w_ {ij} \: = \: \ sum_ {p = 1} ^ P [s_ {i} (p)] [s_ {j} (p)] \: \: \: \: \: for \ : i \: \ neq \: j $$

Algorytm testowania

Step 1 - Zainicjuj wagi, które są uzyskiwane z algorytmu uczącego przy użyciu zasady Hebbiana.

Step 2 - Wykonaj kroki 3-9, jeśli aktywacje sieci nie są skonsolidowane.

Step 3 - Dla każdego wektora wejściowego Xwykonaj kroki 4-8.

Step 4 - Ustaw początkową aktywację sieci równą zewnętrznemu wektorowi wejściowemu X w następujący sposób -

$$ y_ {i} \: = \: x_ {i} \: \: \: dla \: i \: = \: 1 \: do \: n $$

Step 5 - Dla każdej jednostki Y_iwykonaj kroki 6-9.

Step 6 - Obliczyć wejście netto sieci w następujący sposób -

$$ y_ {ini} \: = \: x_ {i} \: + \: \ displaystyle \ sum \ limits_ {j} y_ {j} w_ {ji} $$

Step 7 - Zastosuj aktywację w następujący sposób na wejściu netto, aby obliczyć moc -

$$ y_ {i} \: = \ begin {cases} 1 & if \: y_ {ini} \:> \: \ theta_ {i} \\ y_ {i} & if \: y_ {ini} \: = \: \ theta_ {i} \\ 0 & if \: y_ {ini} \: <\: \ theta_ {i} \ end {cases} $$

Tutaj $ \ theta_ {i} $ jest progiem.

Step 8 - Prześlij to wyjście y_i do wszystkich innych jednostek.

Step 9 - Przetestuj połączenie w sieci.

Ocena funkcji energii

Funkcja energii jest definiowana jako funkcja, która jest powiązaną i nierosnącą funkcją stanu systemu.

Funkcja energii E_f⁡, zwany także Lyapunov function określa stabilność dyskretnej sieci Hopfielda i charakteryzuje się następująco:

$$ E_ {f} \: = \: - \ Frac {1} {2} \ Displaystyle \ sum \ limit_ {i = 1} ^ n \ Displaystyle \ suma \ limity_ {j = 1} ^ n y_ {i} r_ {j} w_ {ij} \: - \: \ displaystyle \ sum \ limit_ {i = 1} ^ n x_ {i} y_ {i} \: + \: \ displaystyle \ sum \ limity_ {i = 1} ^ n \ theta_ {i} y_ {i} $$

Condition - W stabilnej sieci, ilekroć zmienia się stan węzła, powyższa funkcja energetyczna będzie się zmniejszać.

Załóżmy, że node i zmienił stan z $ y_i ^ {(k)} $ na $ y_i ^ {(k \: + \: 1)} $ ⁡, a następnie zmiana energii $ \ Delta E_ {f} $ jest określona przez następującą relację

$$ \ Delta E_ {f} \: = \: E_ {f} (y_i ^ {(k + 1)}) \: - \: E_ {f} (y_i ^ {(k)}) $$

$$ = \: - \ lewo (\ początek {tablica} {c} \ displaystyle \ sum \ limity_ {j = 1} ^ n w_ {ij} y_i ^ {(k)} \: + \: x_ {i} \: - \: \ theta_ {i} \ end {array} \ right) (y_i ^ {(k + 1)} \: - \: y_i ^ {(k)}) $$

$$ = \: - \ :( net_ {i}) \ Delta y_ {i} $$

Tutaj $ \ Delta y_ {i} \: = \: y_i ^ {(k \: + \: 1)} \: - \: y_i ^ {(k)} $

Zmiana energii zależy od tego, że tylko jedna jednostka może aktualizować swoją aktywację na raz.

Ciągła Sieć Hopfielda

W porównaniu z dyskretną siecią Hopfielda, sieć ciągła ma czas jako zmienną ciągłą. Jest również używany w problemach z asocjacjami samochodowymi i optymalizacją, takich jak problem komiwojażera.

Model - Model lub architekturę można zbudować, dodając komponenty elektryczne, takie jak wzmacniacze, które mogą odwzorowywać napięcie wejściowe na napięcie wyjściowe za pomocą funkcji aktywacji sigmoidalnej.

Ocena funkcji energii

$$ E_f = \ Frac {1} {2} \ Displaystyle \ sum \ limity_ {i = 1} ^ n \ suma _ {\ substack {j = 1 \\ j \ ne i}} ^ n y_i y_j w_ {ij} - \ Displaystyle \ suma \ limity_ {i = 1} ^ n x_i y_i + \ Frac {1} {\ lambda} \ Displaystyle \ suma \ limity_ {i = 1} ^ n \ suma _ {\ substack {j = 1 \\ j \ ne i}} ^ n w_ {ij} g_ {ri} \ int_ {0} ^ {y_i} a ^ {- 1} (y) dy $$

Tutaj λ jest parametrem wzmocnienia i g_ri przewodność wejściowa.

Są to stochastyczne procesy uczenia się o powtarzalnej strukturze i stanowią podstawę wczesnych technik optymalizacji stosowanych w SSN. Maszyna Boltzmanna została wynaleziona przez Geoffreya Hintona i Terry'ego Sejnowskiego w 1985 roku. Więcej klarowności można zaobserwować w słowach Hintona na temat Maszyny Boltzmanna.

„Zaskakującą cechą tej sieci jest to, że wykorzystuje ona tylko lokalnie dostępne informacje. Zmiana wagi zależy tylko od zachowania dwóch jednostek, które łączy, chociaż zmiana optymalizuje miarę globalną ”- Ackley, Hinton 1985.

Kilka ważnych punktów na temat maszyny Boltzmanna -

• Używają powtarzalnej struktury.

• Składają się z neuronów stochastycznych, które mają jeden z dwóch możliwych stanów, 1 lub 0.

• Niektóre z neuronów w tym są adaptacyjne (stan wolny), a niektóre są zaciśnięte (stan zamrożony).

• Jeśli zastosujemy symulowane wyżarzanie w dyskretnej sieci Hopfielda, stanie się to maszyną Boltzmanna.

Cel maszyny Boltzmanna

Głównym celem Maszyny Boltzmanna jest optymalizacja rozwiązania problemu. Zadaniem Boltzmanna Machine jest optymalizacja wagi i ilości związanych z tym konkretnym problemem.

Architektura

Poniższy diagram przedstawia architekturę maszyny Boltzmanna. Z diagramu jasno wynika, że ​​jest to dwuwymiarowa tablica jednostek. Tutaj wagi dla połączeń między jednostkami są–p gdzie p > 0. Wagi połączeń samodzielnych są podane przezb gdzie b > 0.

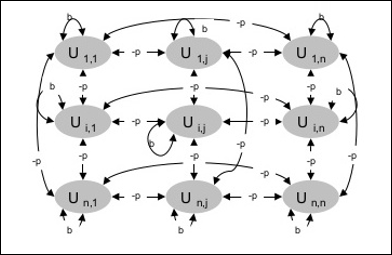
Algorytm treningowy

Ponieważ wiemy, że maszyny Boltzmanna mają stałe wagi, nie będzie algorytmu uczącego, ponieważ nie musimy aktualizować wag w sieci. Aby jednak przetestować sieć, musimy ustawić wagi, a także znaleźć funkcję konsensusu (CF).

Maszyna Boltzmanna posiada zestaw jednostek U_i i U_j i ma na nich połączenia dwukierunkowe.

• Rozważamy ustaloną wagę powiedz w_ij.

• w_ij ≠ 0 Jeśli U_i i U_j są połączone.

• Istnieje również symetria w ważonych wzajemnych połączeniach, tj w_ij = w_ji.

• w_ii istnieje również, tj. istniałoby samo-połączenie między jednostkami.

• Dla każdej jednostki U_i, jego stan u_i byłoby 1 lub 0.

Głównym celem Maszyny Boltzmanna jest maksymalizacja funkcji konsensusu (CF), którą można określić za pomocą następującej relacji

$$ CF \: = \: \ Displaystyle \ sum \ limity_ {i} \ Displaystyle \ sum \ limity_ {j \ leqslant i} w_ {ij} u_ {i} u_ {j} $$

Teraz, gdy stan zmienia się z 1 na 0 lub z 0 na 1, wówczas zmianę w konsensusie można podać następującą relacją -

$$ \ Delta CF \: = \ :( 1 \: - \: 2u_ {i}) (w_ {ij} \: + \: \ displaystyle \ suma \ limit_ {j \ neq i} u_ {i} w_ { ij}) $$

Tutaj u_i to aktualny stan U_i.

Zmienność współczynnika (1 - 2u_i) jest określona zależnością -

$$ (1 \: - \: 2u_ {i}) \: = \: \ begin {cases} +1, & U_ {i} \: is \: obecnie \: wyłączone \\ - 1, & U_ {i } \: jest \: obecnie \: w \ end {przypadkach} $$

Ogólnie jednostka U_inie zmienia swojego stanu, ale jeśli tak się stanie, informacja będzie lokalna dla jednostki. Wraz z tą zmianą nastąpiłby również wzrost konsensusu w sieci.

Prawdopodobieństwo zaakceptowania przez sieć zmiany stanu urządzenia wyraża zależność -

$$ AF (i, T) \: = \: \ frac {1} {1 \: + \: exp [- \ frac {\ Delta CF (i)} {T}]} $$

Tutaj, Tjest parametrem kontrolnym. Zmniejszy się, gdy CF osiągnie wartość maksymalną.

Algorytm testowania

Step 1 - Zainicjuj następujące elementy, aby rozpocząć szkolenie -

• Wagi reprezentujące ograniczenie problemu
• Parametr sterowania T

Step 2 - Kontynuuj kroki 3-8, jeśli warunek zatrzymania nie jest spełniony.

Step 3 - Wykonaj kroki 4-7.

Step 4 - Załóżmy, że jeden ze stanów zmienił wagę i wybierz liczbę całkowitą I, J jako wartości losowe między 1 i n.

Step 5 - Oblicz zmianę konsensusu w następujący sposób -

$$ \ Delta CF \: = \ :( 1 \: - \: 2u_ {i}) (w_ {ij} \: + \: \ displaystyle \ suma \ limit_ {j \ neq i} u_ {i} w_ { ij}) $$

Step 6 - Oblicz prawdopodobieństwo, że ta sieć zaakceptuje zmianę stanu

$$ AF (i, T) \: = \: \ frac {1} {1 \: + \: exp [- \ frac {\ Delta CF (i)} {T}]} $$

Step 7 - Zaakceptuj lub odrzuć tę zmianę w następujący sposób -

Case I - jeśli R < AF, zaakceptuj zmianę.

Case II - jeśli R ≥ AF, odrzuć zmianę.

Tutaj, R to liczba losowa z przedziału od 0 do 1.

Step 8 - Zmniejszyć parametr regulacji (temperaturę) w następujący sposób -

T(new) = ⁡0.95T(old)

Step 9 - Badanie warunków zatrzymania, które mogą być następujące -

• Temperatura osiąga określoną wartość
• Nie ma zmiany stanu dla określonej liczby iteracji

Sieć neuronowa Brain-State-in-a-Box (BSB) jest nieliniową autosocjacyjną siecią neuronową i może być rozszerzona do hetero-asocjacji z dwoma lub więcej warstwami. Jest również podobny do sieci Hopfield. Zaproponowali go JA Anderson, JW Silverstein, SA Ritz i RS Jones w 1977 roku.

Kilka ważnych punktów, o których należy pamiętać o sieci BSB -

• Jest to w pełni połączona sieć z maksymalną liczbą węzłów zależną od wymiarów n przestrzeni wejściowej.

• Wszystkie neurony są aktualizowane jednocześnie.

• Neurony przyjmują wartości od -1 do +1.

Formuły matematyczne

Funkcja węzła używana w sieci BSB to funkcja rampy, którą można zdefiniować w następujący sposób -

$$ f (net) \: = \: min (1, \: max (-1, \: net)) $$

Ta funkcja rampowa jest ograniczona i ciągła.

Ponieważ wiemy, że każdy węzeł zmieniłby swój stan, można to zrobić za pomocą następującej zależności matematycznej -

$$ x_ {t} (t \: + \: 1) \: = \: f \ lewo (\ początek {tablica} {c} \ Displaystyle \ suma \ limity_ {j = 1} ^ n w_ {i, j } x_ {j} (t) \ end {tablica} \ right) $$

Tutaj, x_i(t) jest stanem i_th węzeł w czasie t.

Wagi od i_th węzeł do j_th węzeł można mierzyć za pomocą zależności -

$$ w_ {ij} \: = \: \ Frac {1} {P} \ Displaystyle \ sum \ limits_ {p = 1} ^ P (v_ {p, i} \: v_ {p, j}) $$

Tutaj, P to liczba wzorców treningowych, które są dwubiegunowe.

Optymalizacja to działanie mające na celu uczynienie czegoś takiego jak projekt, sytuacja, zasoby i system tak efektywnymi, jak to tylko możliwe. Wykorzystując podobieństwo między funkcją kosztu a funkcją energii, możemy użyć silnie połączonych neuronów do rozwiązywania problemów optymalizacji. Takim rodzajem sieci neuronowej jest sieć Hopfielda, która składa się z pojedynczej warstwy zawierającej jeden lub więcej w pełni połączonych neuronów powtarzających się. Można to wykorzystać do optymalizacji.

O czym należy pamiętać korzystając z sieci Hopfield do optymalizacji -

• Funkcja energetyczna musi być minimalna dla sieci.

• Znajdzie satysfakcjonujące rozwiązanie zamiast wybrać jeden z zapisanych wzorów.

• Jakość rozwiązania znalezionego przez sieć Hopfield zależy w dużym stopniu od początkowego stanu sieci.

Problem komiwojażera

Znalezienie najkrótszej trasy przebytej przez sprzedawcę to jeden z problemów obliczeniowych, który można zoptymalizować wykorzystując sieć neuronową Hopfield.

Podstawowa koncepcja TSP

Problem komiwojażera (TSP) to klasyczny problem optymalizacyjny, w którym sprzedawca musi podróżować nmiasta, które są ze sobą połączone przy zachowaniu minimalnego kosztu i pokonywanej odległości. Na przykład sprzedawca musi podróżować przez zestaw 4 miast A, B, C, D, a celem jest znalezienie najkrótszej trasy okrężnej, ABC – D, tak aby zminimalizować koszty, które obejmują również koszty podróży z ostatnie miasto D do pierwszego miasta A.

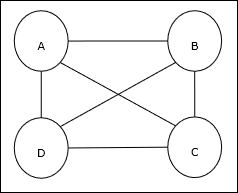
Reprezentacja macierzy

Właściwie każdą wycieczkę po TSP w n-mieście można wyrazić jako n × n macierz, której i_th wiersz opisuje i_thlokalizacja miasta. Ta macierz,M, dla 4 miast A, B, C, D można wyrazić następująco -

$$ M = \ begin {bmatrix} A: & 1 & 0 & 0 & 0 \\ B: & 0 & 1 & 0 & 0 \\ C: & 0 & 0 & 1 & 0 \\ D: & 0 & 0 & 0 & 1 \ end {bmatrix} $$

Rozwiązanie firmy Hopfield Network

Rozważając rozwiązanie tego TSP przez sieć Hopfielda, każdemu węzłowi w sieci odpowiada jeden element macierzy.

Obliczanie funkcji energii

Aby było optymalnym rozwiązaniem, funkcja energii musi być minimalna. Na podstawie następujących ograniczeń możemy obliczyć funkcję energii w następujący sposób -

Ograniczenie-I

Pierwszym ograniczeniem, na podstawie którego obliczymy funkcję energii, jest to, że jeden element musi być równy 1 w każdym wierszu macierzy M a inne elementy w każdym wierszu muszą być równe 0ponieważ każde miasto może występować tylko w jednym miejscu w trasie TSP. To ograniczenie można zapisać matematycznie w następujący sposób -

$$ \ Displaystyle \ suma \ limity_ {j = 1} ^ n M_ {x, j} \: = \: 1 \: dla \: x \: \ in \: \ lbrace1, ..., n \ rbrace $ $

Teraz funkcja energii, która ma zostać zminimalizowana, w oparciu o powyższe ograniczenie, będzie zawierała człon proporcjonalny do -

$$ \ Displaystyle \ suma \ limity_ {x = 1} ^ n \ lewo (\ początek {tablica} {c} 1 \: - \: \ Displaystyle \ suma \ limity_ {j = 1} ^ n M_ {x, j } \ end {tablica} \ right) ^ 2 $$

Ograniczenie-II

Jak wiemy, w TSP jedno miasto może występować w dowolnej pozycji w trasie, stąd w każdej kolumnie macierzy M, jeden element musi być równy 1, a inne elementy muszą być równe 0. To ograniczenie można matematycznie zapisać w następujący sposób -

$$ \ Displaystyle \ suma \ limity_ {x = 1} ^ n M_ {x, j} \: = \: 1 \: dla \: j \: \ in \: \ lbrace1, ..., n \ rbrace $ $

Teraz funkcja energii, która ma zostać zminimalizowana, w oparciu o powyższe ograniczenie, będzie zawierała człon proporcjonalny do -

$$ \ Displaystyle \ suma \ limity_ {j = 1} ^ n \ lewo (\ początek {tablica} {c} 1 \: - \: \ Displaystyle \ suma \ limity_ {x = 1} ^ n M_ {x, j } \ end {tablica} \ right) ^ 2 $$

Obliczanie funkcji kosztów

Załóżmy, że macierz kwadratową (n × n) oznaczony przez C oznacza macierz kosztów TSP dla n miasta, w których n > 0. Poniżej przedstawiono kilka parametrów podczas obliczania funkcji kosztu -

• C_{x, y} - Element macierzy kosztów oznacza koszt dojazdu z miasta x do y.

• Sąsiedztwo elementów A i B można przedstawić za pomocą następującej zależności -

$$ M_ {x, i} \: = \: 1 \: \: and \: \: M_ {y, i \ pm 1} \: = \: 1 $$

Jak wiemy, w Matrixie wartość wyjściowa każdego węzła może wynosić 0 lub 1, stąd dla każdej pary miast A, B możemy dodać następujące wyrażenia do funkcji energii -

$$ \ Displaystyle \ suma \ limity_ {i = 1} ^ n C_ {x, y} M_ {x, i} (M_ {y, i + 1} \: + \: M_ {y, i-1}) $$

Na podstawie powyższej funkcji kosztu i wartości ograniczenia, funkcja energii końcowej E można podać w następujący sposób -

$$ E \: = \: \ Frac {1} {2} \ Displaystyle \ sum \ limity_ {i = 1} ^ n \ Displaystyle \ suma \ limity_ {x} \ Displaystyle \ suma \ limity_ {y \ neq x} C_ {x, y} M_ {x, i} (M_ {y, i + 1} \: + \: M_ {y, i-1}) \: + $$

$$ \: \ początek {bmatrix} \ gamma_ {1} \ Displaystyle \ sum \ limit_ {x} \ lewo (\ początek {tablica} {c} 1 \: - \: \ displaystyle \ sum \ limity_ {i} M_ {x, i} \ koniec {tablica} \ po prawej) ^ 2 \: + \: \ gamma_ {2} \ displaystyle \ sum \ limit_ {i} \ lewo (\ początek {tablica} {c} 1 \: - \ : \ Displaystyle \ suma \ limity_ {x} M_ {x, i} \ koniec {tablica} \ po prawej) ^ 2 \ koniec {bmatrix} $$

Tutaj, γ₁ i γ₂ są dwiema stałymi ważenia.

Technika Iterowanego Zejścia Gradientu

Zejście gradientowe, nazywane również najbardziej stromym zejściem, to iteracyjny algorytm optymalizacji służący do znalezienia lokalnego minimum funkcji. Minimalizując tę ​​funkcję, obawiamy się o koszt lub błąd, który należy zminimalizować (Pamiętaj o problemie komiwojażera). Jest szeroko stosowany w głębokim uczeniu się, co jest przydatne w wielu różnych sytuacjach. Należy tutaj pamiętać, że zajmujemy się optymalizacją lokalną, a nie globalną.

Główny pomysł roboczy

Możemy zrozumieć główną ideę roboczą spadku gradientu za pomocą następujących kroków -

• Najpierw zacznij od wstępnego odgadnięcia rozwiązania.

• Następnie weź gradient funkcji w tym punkcie.

• Później powtórz proces, przesuwając roztwór w kierunku ujemnym gradientu.

Postępując zgodnie z powyższymi krokami, algorytm ostatecznie zbiegnie się tam, gdzie gradient wynosi zero.

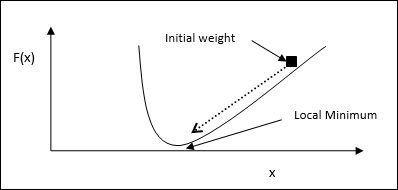
Pojęcie matematyczne

Załóżmy, że mamy funkcję f(x)i staramy się znaleźć minimum tej funkcji. Poniżej przedstawiono kroki, aby znaleźć minimumf(x).

• Najpierw podaj początkową wartość $ x_ {0} \: for \: x $

• Teraz weź gradient funkcji $ \ nabla f $ ⁡of, mając intuicję, że gradient da nachylenie krzywej w tym miejscu x a jej kierunek wskaże wzrost funkcji, aby znaleźć najlepszy kierunek jej zminimalizowania.

• Teraz zmień x w następujący sposób -

  $$ x_ {n \: + \: 1} \: = \: x_ {n} \: - \: \ theta \ nabla f (x_ {n}) $$

Tutaj, θ > 0 to szybkość uczenia (wielkość kroku), która zmusza algorytm do wykonywania małych skoków.

Szacowanie wielkości kroku

Właściwie zły rozmiar kroku θmoże nie osiągnąć konwergencji, dlatego bardzo ważny jest ich staranny dobór. Przy wyborze rozmiaru kroku należy pamiętać o następujących punktach

• Nie wybieraj zbyt dużego rozmiaru kroku, w przeciwnym razie będzie to miało negatywny wpływ, tj. Będzie się raczej rozchodzić niż zbiegać.

• Nie wybieraj zbyt małego rozmiaru kroku, w przeciwnym razie zbieżność zajmie dużo czasu.

Niektóre opcje dotyczące wyboru rozmiaru stopnia -

• Jedną z opcji jest wybranie stałego rozmiaru kroku.

• Inną opcją jest wybranie innego rozmiaru kroku dla każdej iteracji.

Symulowanego wyżarzania

Podstawowa koncepcja symulowanego wyżarzania (SA) jest motywowana wyżarzaniem w ciałach stałych. Jeśli w procesie wyżarzania podgrzejemy metal powyżej jego temperatury topnienia i ostudzimy, to właściwości strukturalne będą zależały od szybkości chłodzenia. Można też powiedzieć, że SA symuluje metalurgiczny proces wyżarzania.

Użyj w ANN

SA jest stochastyczną metodą obliczeniową, inspirowaną analogią wyżarzania, służącą do przybliżania globalnej optymalizacji danej funkcji. Możemy użyć SA do uczenia sieci neuronowych typu feed-forward.

Algorytm

Step 1 - Wygeneruj losowe rozwiązanie.

Step 2 - Oblicz jego koszt za pomocą funkcji kosztu.

Step 3 - Wygeneruj losowo sąsiednie rozwiązanie.

Step 4 - Oblicz koszt nowego rozwiązania według tej samej funkcji kosztu.

Step 5 - Porównaj koszt nowego rozwiązania z kosztem starego rozwiązania w następujący sposób -

Jeśli Cost_{New Solution} < Cost_{Old Solution} następnie przejdź do nowego rozwiązania.

Step 6 - Sprawdź warunek zatrzymania, którym może być maksymalna liczba osiągniętych iteracji lub uzyskaj akceptowalne rozwiązanie.

Natura zawsze była wielkim źródłem inspiracji dla całej ludzkości. Algorytmy genetyczne (GA) to algorytmy oparte na wyszukiwaniu, oparte na koncepcjach doboru naturalnego i genetyki. GA są podzbiorem znacznie większej gałęzi obliczeń znanej jakoEvolutionary Computation.

GA zostały opracowane przez Johna Hollanda oraz jego studentów i współpracowników z University of Michigan, w szczególności Davida E. Goldberga, i od tego czasu były testowane z dużym powodzeniem w różnych problemach optymalizacyjnych.

W AH mamy pulę lub populację możliwych rozwiązań danego problemu. Następnie roztwory te ulegają rekombinacji i mutacji (podobnie jak w genetyce naturalnej), rodząc nowe dzieci, a proces ten powtarza się przez różne pokolenia. Każdej osobie (lub proponowanemu rozwiązaniu) przypisywana jest wartość przystosowania (oparta na wartości funkcji celu), a sprawniejsze osobniki mają większą szansę na kojarzenie się i wydanie bardziej „sprawniejszych” osobników. Jest to zgodne z darwinowską teorią „przetrwania najsilniejszych”.

W ten sposób nieustannie „rozwijamy” lepsze jednostki lub rozwiązania przez pokolenia, aż osiągniemy kryterium zatrzymania.

Algorytmy genetyczne mają wystarczająco losowy charakter, jednak działają znacznie lepiej niż losowe wyszukiwanie lokalne (w którym po prostu próbujemy różnych losowych rozwiązań, śledząc najlepsze do tej pory), ponieważ wykorzystują również informacje historyczne.

Zalety GA

GA mają różne zalety, dzięki którym są niezwykle popularne. Należą do nich -

• Nie wymaga żadnych informacji pochodnych (które mogą nie być dostępne w przypadku wielu rzeczywistych problemów).

• Jest szybszy i wydajniejszy w porównaniu do metod tradycyjnych.

• Posiada bardzo dobre możliwości równoległe.

• Optymalizuje zarówno funkcje ciągłe i dyskretne, jak i problemy z wieloma celami.

• Zawiera listę „dobrych” rozwiązań, a nie tylko pojedyncze rozwiązanie.

• Zawsze otrzymuje odpowiedź na problem, która z czasem staje się coraz lepsza.

• Przydatne, gdy przestrzeń wyszukiwania jest bardzo duża i występuje duża liczba parametrów.

Ograniczenia GA

Jak każda technika, GA również ma kilka ograniczeń. Należą do nich -

• GA nie są dostosowane do wszystkich problemów, zwłaszcza problemów, które są proste i dla których dostępne są informacje pochodne.

• Wartość sprawności jest obliczana wielokrotnie, co może być kosztowne obliczeniowo w przypadku niektórych problemów.

• Będąc stochastycznym, nie ma gwarancji co do optymalności ani jakości rozwiązania.

• Jeśli nie zostanie prawidłowo wdrożony, GA może nie doprowadzić do osiągnięcia optymalnego rozwiązania.

GA - Motywacja

Algorytmy genetyczne są w stanie dostarczyć „wystarczająco dobre” rozwiązanie „wystarczająco szybko”. To sprawia, że ​​Gas jest atrakcyjny do wykorzystania w rozwiązywaniu problemów optymalizacyjnych. Powody, dla których potrzebne są GA, są następujące -

Rozwiązywanie trudnych problemów

W informatyce istnieje wiele problemów, którymi są NP-Hard. W istocie oznacza to, że rozwiązanie tego problemu nawet w przypadku najpotężniejszych systemów komputerowych zajmuje bardzo dużo czasu (nawet lata!). W takim scenariuszu GA okazują się skutecznym narzędziem dostarczaniausable near-optimal solutions w krótkim czasie.

Niepowodzenie metod opartych na gradientach

Tradycyjne metody oparte na rachunku różniczkowym działają na zasadzie startu w losowym punkcie i poruszania się zgodnie z kierunkiem nachylenia, aż osiągniemy szczyt wzgórza. Ta technika jest wydajna i działa bardzo dobrze w przypadku funkcji celu z pojedynczym szczytem, ​​takich jak funkcja kosztu w regresji liniowej. Jednak w większości rzeczywistych sytuacji mamy bardzo złożony problem zwany krajobrazami, składający się z wielu szczytów i wielu dolin, co powoduje, że takie metody zawodzą, ponieważ cierpią z powodu nieodłącznej tendencji do utknięcia w lokalnych optymach, jak pokazano na poniższym rysunku.

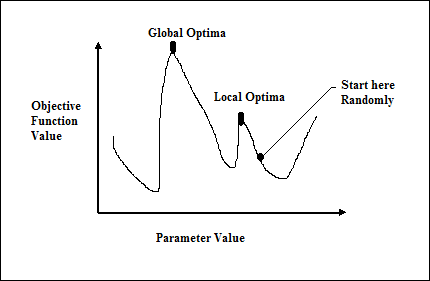
Szybkie uzyskanie dobrego rozwiązania

Niektóre trudne problemy, takie jak problem komiwojażera (TSP), mają zastosowania w świecie rzeczywistym, takie jak wyszukiwanie ścieżek i projektowanie VLSI. Teraz wyobraź sobie, że korzystasz z systemu nawigacji GPS i obliczenie „optymalnej” ścieżki od źródła do celu zajmuje kilka minut (lub nawet kilka godzin). Opóźnienia w takich rzeczywistych zastosowaniach są nie do przyjęcia, dlatego wymagane jest „wystarczająco dobre” rozwiązanie, które jest dostarczane „szybko”.

Jak używać Google Analytics do rozwiązywania problemów z optymalizacją?

Wiemy już, że optymalizacja to działanie mające na celu uczynienie czegoś takiego jak projekt, sytuacja, zasoby i system tak efektywnymi, jak to tylko możliwe. Proces optymalizacji przedstawia poniższy diagram.

Etapy mechanizmu GA dla procesu optymalizacji

Poniżej przedstawiono etapy mechanizmu GA używanego do optymalizacji problemów.

• Generuj losowo początkową populację.

• Wybierz początkowe rozwiązanie z najlepszymi wartościami sprawności.

• Ponownie połącz wybrane rozwiązania za pomocą operatorów mutacji i krzyżowania.

• Wstaw potomstwo do populacji.

• Teraz, jeśli warunek zatrzymania jest spełniony, zwróć rozwiązanie z najlepszą wartością dopasowania. W przeciwnym razie przejdź do kroku 2.

Przed zbadaniem dziedzin, w których SSN była szeroko stosowana, musimy zrozumieć, dlaczego SSN byłaby preferowanym wyborem zastosowania.

Dlaczego sztuczne sieci neuronowe?

Odpowiedź na powyższe pytanie musimy rozumieć na przykładzie człowieka. Jako dziecko uczyliśmy się tego z pomocą starszych, w tym rodziców lub nauczycieli. Później poprzez samokształcenie lub praktykę uczymy się przez całe życie. Naukowcy i badacze również czynią maszynę inteligentną, tak jak człowiek, a SSN odgrywa w tym samym bardzo ważną rolę z następujących powodów:

• Za pomocą sieci neuronowych możemy znaleźć rozwiązanie takich problemów, dla których metoda algorytmiczna jest kosztowna lub nie istnieje.

• Sieci neuronowe mogą uczyć się na przykładach, dlatego nie musimy ich w dużym stopniu programować.

• Sieci neuronowe charakteryzują się dokładnością i znacznie większą szybkością niż prędkość konwencjonalna.

Obszary zastosowań

Oto niektóre obszary, w których używana jest SSN. Sugeruje to, że SSN ma interdyscyplinarne podejście do tworzenia i zastosowań.

Rozpoznawanie mowy

Mowa odgrywa znaczącą rolę w interakcji człowiek-człowiek. Dlatego naturalne jest, że ludzie oczekują interfejsów głosowych z komputerami. W dzisiejszych czasach do komunikacji z maszynami ludzie nadal potrzebują wyrafinowanych języków, których trudno się nauczyć i używać. Aby złagodzić tę barierę komunikacyjną, prostym rozwiązaniem może być komunikacja w języku mówionym, który jest zrozumiały dla maszyny.

W tej dziedzinie dokonał się duży postęp, jednak nadal tego rodzaju systemy borykają się z problemem ograniczonego słownictwa czy gramatyki oraz problemem przekwalifikowania systemu dla różnych mówców w różnych warunkach. SSN odgrywa ważną rolę w tej dziedzinie. Następujące SSN zostały użyte do rozpoznawania mowy:

• Sieci wielowarstwowe

• Sieci wielowarstwowe z powtarzającymi się połączeniami

• Samoorganizująca się mapa funkcji Kohonen

Najbardziej użyteczną siecią do tego jest samoorganizująca się mapa funkcji Kohonen, która ma swoje dane wejściowe w postaci krótkich segmentów przebiegu mowy. Będzie odwzorowywać ten sam rodzaj fonemów, co tablica wyjściowa, zwany techniką ekstrakcji cech. Po wyodrębnieniu cech, z pomocą niektórych modeli akustycznych jako przetwarzania końcowego, rozpozna wypowiedź.

Rozpoznawanie postaci

Jest to interesujący problem, który mieści się w ogólnym obszarze rozpoznawania wzorców. Opracowano wiele sieci neuronowych do automatycznego rozpoznawania odręcznych znaków, liter lub cyfr. Poniżej przedstawiono niektóre SSN, które były używane do rozpoznawania znaków -

• Wielowarstwowe sieci neuronowe, takie jak sieci neuronowe z propagacją wsteczną.
• Neocognitron

Chociaż sieci neuronowe wykorzystujące propagację wsteczną mają kilka ukrytych warstw, lokalizowany jest schemat połączeń między warstwami. Podobnie, neokognitron ma również kilka ukrytych warstw, a jego trening odbywa się warstwa po warstwie dla tego rodzaju zastosowań.

Wniosek o weryfikację podpisu

Podpisy to jeden z najbardziej użytecznych sposobów autoryzacji i uwierzytelnienia osoby w transakcjach prawnych. Technika weryfikacji sygnatury nie jest oparta na wizji.

W przypadku tego zastosowania pierwszym podejściem jest wyodrębnienie cechy lub raczej zestawu cech geometrycznych reprezentujących sygnaturę. Dzięki tym zestawom funkcji musimy trenować sieci neuronowe przy użyciu wydajnego algorytmu sieci neuronowej. Ta wyszkolona sieć neuronowa będzie klasyfikować podpis jako autentyczny lub sfałszowany na etapie weryfikacji.

Rozpoznawanie twarzy człowieka

Jest to jedna z biometrycznych metod identyfikacji twarzy. Jest to typowe zadanie ze względu na charakterystykę obrazów „innych niż twarze”. Jeśli jednak sieć neuronowa jest dobrze wytrenowana, to można ją podzielić na dwie klasy, a mianowicie obrazy zawierające twarze i obrazy, które nie mają twarzy.

Po pierwsze, wszystkie obrazy wejściowe muszą zostać wstępnie przetworzone. Następnie należy zmniejszyć wymiarowość tego obrazu. I wreszcie musi zostać sklasyfikowany przy użyciu algorytmu uczenia sieci neuronowej. Następujące sieci neuronowe są używane do celów szkoleniowych z wstępnie przetworzonym obrazem -

• W pełni połączona wielowarstwowa sieć neuronowa ze sprzężeniem zwrotnym, trenowana za pomocą algorytmu propagacji wstecznej.

• W celu redukcji wymiarowości stosowana jest analiza głównych komponentów (PCA).