Nauka kwantyzacji wektorów
Nauka kwantyzacji wektorów (LVQ), różni się od kwantyzacji wektorów (VQ) i map samoorganizujących się Kohonena (KSOM), jest w zasadzie konkurencyjną siecią, która wykorzystuje nadzorowane uczenie się. Możemy zdefiniować to jako proces klasyfikowania wzorców, w których każda jednostka wyjściowa reprezentuje klasę. Ponieważ wykorzystuje uczenie nadzorowane, sieć otrzyma zestaw wzorców uczących ze znaną klasyfikacją wraz z początkową dystrybucją klasy wyjściowej. Po zakończeniu procesu uczenia LVQ sklasyfikuje wektor wejściowy, przypisując go do tej samej klasy, co jednostka wyjściowa.
Architektura
Poniższy rysunek przedstawia architekturę LVQ, która jest dość podobna do architektury KSOM. Jak widać, są“n” liczba jednostek wejściowych i “m”liczba jednostek wyjściowych. Warstwy są w pełni połączone ze sobą i mają na sobie ciężarki.

Używane parametry
Poniżej przedstawiono parametry używane w procesie uczenia LVQ, a także w schemacie blokowym
x= wektor uczący (x 1 , ..., x i , ..., x n )
T = klasa dla wektora szkoleniowego x
wj = wektor wagi dla jth jednostka wyjściowa
Cj = klasa skojarzona z jth jednostka wyjściowa
Algorytm treningowy
Step 1 - Zainicjuj wektory odniesienia, co można zrobić w następujący sposób -
Step 1(a) - Z podanego zestawu wektorów uczących weź pierwszy „m”(Liczba klastrów) wektorów uczących i używaj ich jako wektorów wagi. Pozostałe wektory można wykorzystać do treningu.
Step 1(b) - Losowo przypisz wagę początkową i klasyfikację.
Step 1(c) - Zastosuj metodę grupowania średnich wartości K.
Step 2 - Zainicjuj wektor odniesienia $ \ alpha $
Step 3 - Kontynuuj kroki 4-9, jeśli warunek zatrzymania tego algorytmu nie jest spełniony.
Step 4 - Wykonaj kroki 5-6 dla każdego wektora wejściowego szkolenia x.
Step 5 - Oblicz kwadrat odległości euklidesowej dla j = 1 to m i i = 1 to n
$$ D (j) \: = \: \ Displaystyle \ suma \ limity_ {i = 1} ^ n \ Displaystyle \ suma \ limity_ {j = 1} ^ m (x_ {i} \: - \: w_ {ij }) ^ 2 $$
Step 6 - Zdobądź zwycięską jednostkę J gdzie D(j) jest minimum.
Step 7 - Oblicz nową wagę zwycięskiej jednostki za pomocą następującej zależności -
gdyby T = Cj następnie $ w_ {j} (nowy) \: = \: w_ {j} (stary) \: + \: \ alpha [x \: - \: w_ {j} (stary)] $
gdyby T ≠ Cj następnie $ w_ {j} (nowy) \: = \: w_ {j} (stary) \: - \: \ alpha [x \: - \: w_ {j} (stary)] $
Step 8 - Zmniejsz współczynnik uczenia się $ \ alpha $.
Step 9- Sprawdź stan zatrzymania. Może wyglądać następująco -
- Osiągnięto maksymalną liczbę epok.
- Szybkość uczenia się zredukowana do znikomej wartości.
Schemat blokowy
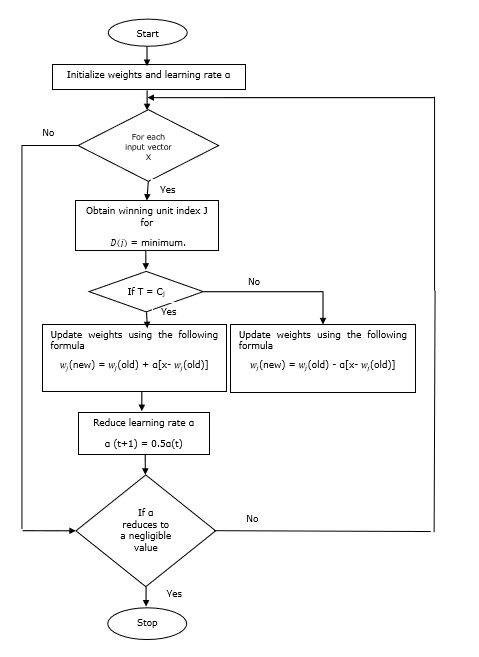
Warianty
Trzy inne warianty, a mianowicie LVQ2, LVQ2.1 i LVQ3, zostały opracowane przez Kohonena. Złożoność we wszystkich tych trzech wariantach, ze względu na koncepcję, której nauczy się zarówno zwycięzca, jak i jednostka zajmująca drugie miejsce, jest większa niż w LVQ.
LVQ2
Jak omówiono powyżej, koncepcja innych wariantów LVQ, stan LVQ2 jest tworzony przez okno. To okno będzie oparte na następujących parametrach -
x - aktualny wektor wejściowy
yc - wektor odniesienia najbliższy x
yr - inny wektor odniesienia, który jest następny najbliżej x
dc - odległość od x do yc
dr - odległość od x do yr
Wektor wejściowy x wpadnie w okno, jeśli
$$ \ frac {d_ {c}} {d_ {r}} \:> \: 1 \: - \: \ theta \: \: i \: \: \ frac {d_ {r}} {d_ {c }} \:> \: 1 \: + \: \ theta $$
Tutaj $ \ theta $ to liczba próbek treningowych.
Aktualizację można przeprowadzić za pomocą następującego wzoru -
$ y_ {c} (t \: + \: 1) \: = \: y_ {c} (t) \: + \: \ alpha (t) [x (t) \: - \: y_ {c} (t)] $ (belongs to different class)
$ y_ {r} (t \: + \: 1) \: = \: y_ {r} (t) \: + \: \ alpha (t) [x (t) \: - \: y_ {r} (t)] $ (belongs to same class)
Tutaj $ \ alpha $ to współczynnik uczenia się.
LVQ2.1
W LVQ2.1 weźmiemy dwa najbliższe wektory, a mianowicie yc1 i yc2 a stan okna jest następujący -
$$ Min \ begin {bmatrix} \ frac {d_ {c1}} {d_ {c2}}, \ frac {d_ {c2}} {d_ {c1}} \ end {bmatrix} \:> \ :( 1 \ : - \: \ theta) $$
$$ Max \ begin {bmatrix} \ frac {d_ {c1}} {d_ {c2}}, \ frac {d_ {c2}} {d_ {c1}} \ end {bmatrix} \: <\ :( 1 \ : + \: \ theta) $$
Aktualizację można przeprowadzić za pomocą następującego wzoru -
$ y_ {c1} (t \: + \: 1) \: = \: y_ {c1} (t) \: + \: \ alpha (t) [x (t) \: - \: y_ {c1} (t)] $ (belongs to different class)
$ y_ {c2} (t \: + \: 1) \: = \: y_ {c2} (t) \: + \: \ alpha (t) [x (t) \: - \: y_ {c2} (t)] $ (belongs to same class)
Tutaj $ \ alpha $ to współczynnik uczenia się.
LVQ3
W LVQ3 weźmiemy dwa najbliższe wektory, a mianowicie yc1 i yc2 a stan okna jest następujący -
$$ Min \ begin {bmatrix} \ frac {d_ {c1}} {d_ {c2}}, \ frac {d_ {c2}} {d_ {c1}} \ end {bmatrix} \:> \ :( 1 \ : - \: \ theta) (1 \: + \: \ theta) $$
Tutaj $ \ theta \ około 0,2 $
Aktualizację można przeprowadzić za pomocą następującego wzoru -
$ y_ {c1} (t \: + \: 1) \: = \: y_ {c1} (t) \: + \: \ beta (t) [x (t) \: - \: y_ {c1} (t)] $ (belongs to different class)
$ y_ {c2} (t \: + \: 1) \: = \: y_ {c2} (t) \: + \: \ beta (t) [x (t) \: - \: y_ {c2} (t)] $ (belongs to same class)
Tutaj $ \ beta $ jest wielokrotnością współczynnika uczenia się $ \ alpha $ i $\beta\:=\:m \alpha(t)$ dla każdego 0.1 < m < 0.5