Samoorganizujące się mapy funkcji Kohonena
Załóżmy, że mamy jakiś wzór dowolnych wymiarów, jednak potrzebujemy ich w jednym lub dwóch wymiarach. Wtedy proces mapowania cech byłby bardzo przydatny do przekształcenia szerokiej przestrzeni wzorców w typową przestrzeń cech. Teraz pojawia się pytanie, dlaczego potrzebujemy samoorganizującej się mapy cech? Powodem jest to, że oprócz możliwości konwersji dowolnych wymiarów na 1-D lub 2-D, musi mieć również możliwość zachowania sąsiedniej topologii.
Sąsiednie topologie w Kohonen SOM
Mogą istnieć różne topologie, jednak najczęściej używane są dwie następujące topologie -
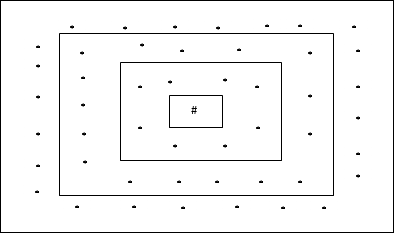
Prostokątna topologia siatki
Ta topologia ma 24 węzły w siatce odległość-2, 16 węzłów w siatce odległość-1 i 8 węzłów w siatce odległość-0, co oznacza, że różnica między każdą siatką prostokątną wynosi 8 węzłów. Zwycięska jednostka jest oznaczona przez #.
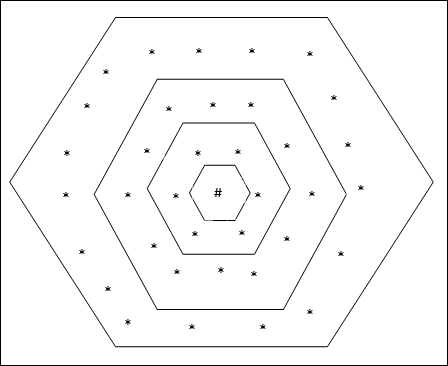
Sześciokątna topologia siatki
Ta topologia ma 18 węzłów w siatce odległość-2, 12 węzłów w siatce odległość-1 i 6 węzłów w siatce odległość-0, co oznacza, że różnica między każdą siatką prostokątną wynosi 6 węzłów. Zwycięska jednostka jest oznaczona przez #.
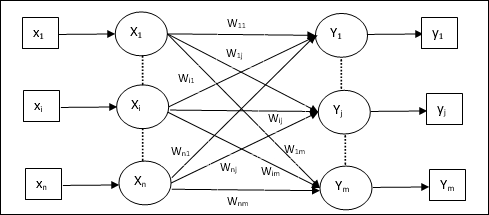
Architektura
Architektura KSOM jest podobna do sieci konkurencyjnej. Za pomocą omówionych wcześniej schematów sąsiedzkich szkolenie może odbywać się w rozszerzonym regionie sieci.
Algorytm do treningu
Step 1 - Zainicjuj wagi, tempo uczenia się α i schemat topologii sąsiedztwa.
Step 2 - Kontynuuj krok 3-9, jeśli warunek zatrzymania nie jest spełniony.
Step 3 - Kontynuuj krok 4-6 dla każdego wektora wejściowego x.
Step 4 - Oblicz kwadrat odległości euklidesowej dla j = 1 to m
$$ D (j) \: = \: \ Displaystyle \ suma \ limity_ {i = 1} ^ n \ Displaystyle \ suma \ limity_ {j = 1} ^ m (x_ {i} \: - \: w_ {ij }) ^ 2 $$
Step 5 - Zdobądź zwycięską jednostkę J gdzie D(j) jest minimum.
Step 6 - Oblicz nową wagę zwycięskiej jednostki za pomocą następującej zależności -
$$ w_ {ij} (nowy) \: = \: w_ {ij} (stary) \: + \: \ alpha [x_ {i} \: - \: w_ {ij} (stary)] $$
Step 7 - Zaktualizuj współczynnik uczenia się α przez następującą relację -
$$ \ alpha (t \: + \: 1) \: = \: 0.5 \ alpha t $$
Step 8 - Zmniejsz promień schematu topologicznego.
Step 9 - Sprawdź stan zatrzymania sieci.