Matematyka dyskretna - teoria grup

Półgrupa

Skończony lub nieskończony zbiór $ 'S' $ z operacją binarną $ '\ omicron' $ (Skład) nazywany jest półgrupą, jeśli spełnia jednocześnie dwa warunki -

Closure - Dla każdej pary $ (a, b) \ in S, \ :( a \ omicron b) $ musi znajdować się w zbiorze $ S $.
Associative - Dla każdego elementu $ a, b, c \ in S, (a \ omicron b) \ omicron c = a \ omicron (b \ omicron c) $ musi być zachowane.

Przykład

Zbiór dodatnich liczb całkowitych (bez zera) z operacją dodawania jest półgrupą. Na przykład $ S = \ lbrace 1, 2, 3, \ dots \ rbrace $

Tutaj właściwość domknięcia zachodzi jak dla każdej pary $ (a, b) \ w S, (a + b) $ występuje w zbiorze S. Na przykład $ 1 + 2 = 3 \ in S] $

Własność asocjacyjna zachodzi również dla każdego elementu $ a, b, c \ w S, (a + b) + c = a + (b + c) $. Na przykład $ (1 + 2) + 3 = 1 + (2 + 3) = 5 $

Monoid

Monoid to półgrupa z elementem tożsamości. Element tożsamości (oznaczony przez $ e $ lub E) zbioru S jest takim elementem, że $ (a \ omicron e) = a $, dla każdego elementu $ a \ w S $. Element tożsamości jest również nazywanyunit element. Zatem monoid posiada jednocześnie trzy właściwości -Closure, Associative, Identity element.

Przykład

Zbiór dodatnich liczb całkowitych (z wyłączeniem zera) z operacją mnożenia jest monoidem. $ S = \ lbrace 1, 2, 3, \ dots \ rbrace $

Tutaj właściwość domknięcia zachodzi tak, jak dla każdej pary $ (a, b) \ w S, (a \ razy b) $ występuje w zbiorze S. [Na przykład $ 1 \ razy 2 = 2 \ w S $ i tak dalej]

Własność asocjacyjna zachodzi również dla każdego elementu $ a, b, c \ in S, (a \ times b) \ times c = a \ times (b \ times c) $ [Na przykład $ (1 \ times 2) \ times 3 = 1 \ times (2 \ times 3) = 6 $ i tak dalej]

Właściwość tożsamości zachowuje się również dla każdego elementu $ a \ in S, (a \ times e) = a $ [Na przykład $ (2 \ times 1) = 2, (3 \ times 1) = 3 $ i tak dalej]. Tutaj elementem tożsamości jest 1.

Grupa

Grupa jest monoidem z elementem odwrotnym. Odwrotny element (oznaczony I) zbioru S jest takim elementem, że $ (a \ omicron I) = (I \ omicron a) = a $, dla każdego elementu $ a \ in S $. Zatem grupa posiada jednocześnie cztery własności - i) Zamknięcie, ii) Asocjację, iii) Element tożsamości, iv) Element odwrotny. Kolejność grupy G to liczba elementów w G, a kolejność elementów w grupie to najmniejsza dodatnia liczba całkowita n taka, że an jest elementem tożsamości tej grupy G.

Przykłady

Zbiór $ N \ razy N $ niejednostkowych macierzy tworzy grupę podlegającą operacji mnożenia macierzy.

Iloczyn dwóch $ N \ razy N $ niejednostkowych macierzy jest również niejednostkową macierzą $ N \ razy N $, która posiada właściwość domknięcia.

Mnożenie macierzy samo w sobie jest asocjacyjne. Stąd własność asocjacyjna zachodzi.

Zbiór $ N \ razy N $ niejednostkowych macierzy zawiera macierz tożsamości przechowującą właściwość elementu tożsamości.

Ponieważ wszystkie macierze nie są pojedyncze, wszystkie mają odwrotne elementy, które są również macierzami nieosobowymi. Stąd też zachodzi własność odwrotna.

Grupa abelowa

Grupa abelowa G to grupa, dla której para elementów $ (a, b) \ in G $ zawsze ma prawo przemienne. Tak więc grupa posiada pięć właściwości jednocześnie - i) Zamknięcie, ii) Asocjacyjne, iii) Element tożsamości, iv) Element odwrotny, v) Przemienność.

Przykład

Zbiór dodatnich liczb całkowitych (w tym zera) z operacją dodawania jest grupą abelową. $ G = \ lbrace 0, 1, 2, 3, \ dots \ rbrace $

Tutaj właściwość domknięcia zachowuje się tak, jak dla każdej pary $ (a, b) \ w S, (a + b) $ występuje w zbiorze S. [Na przykład $ 1 + 2 = 2 \ w S $ i tak dalej]

Własność asocjacyjna zachodzi również dla każdego elementu $ a, b, c \ in S, (a + b) + c = a + (b + c) $ [Na przykład $ (1 +2) + 3 = 1 + (2 + 3) = 6 $ i tak dalej]

Własność przemienna zachodzi również dla każdego elementu $ a \ in S, (a \ times b) = (b \ times a) $ [Na przykład $ (2 \ times 3) = (3 \ times 2) = 3 $ i tak na]

Grupa cykliczna i podgrupa

ZA cyclic groupto grupa, którą może wygenerować pojedynczy element. Każdy element grupy cyklicznej jest potęgą jakiegoś określonego elementu, który nazywamy generatorem. Grupa cykliczna może być generowana przez generator „g”, tak że każdy inny element grupy można zapisać jako moc generatora „g”.

Przykład

Zbiór liczb zespolonych $ \ lbrace 1, -1, i, -i \ rbrace $ w ramach operacji mnożenia jest grupą cykliczną.

Istnieją dwa generatory - $ i $ i $ –i $ jako $ i ^ 1 = i, i ^ 2 = -1, i ^ 3 = -i, i ^ 4 = 1 $, a także $ (- i) ^ 1 = -i, (–i) ^ 2 = -1, (–i) ^ 3 = i, (–i) ^ 4 = 1 $, który obejmuje wszystkie elementy grupy. Dlatego jest to grupa cykliczna.

Note - A cyclic groupjest zawsze grupą abelową, ale nie każda grupa abelowa jest grupą cykliczną. Dodawane liczby wymierne nie są cykliczne, ale abelowe.

ZA subgroup H jest podzbiorem grupy G (oznaczonej przez $ H ≤ G $), jeśli spełnia jednocześnie cztery właściwości - Closure, Associative, Identity element, i Inverse.

Podgrupa H grupy G, która nie obejmuje całej grupy G, nazywana jest odpowiednią podgrupą (oznaczona jako $ H <G $). Podgrupa grupy cyklicznej jest cykliczna, a podgrupa abelowa jest również abelowa.

Przykład

Niech grupa $ G = \ lbrace 1, i, -1, -i \ rbrace $

Wtedy niektóre podgrupy to $ H_1 = \ lbrace 1 \ rbrace, H_2 = \ lbrace 1, -1 \ rbrace $,

To nie jest podgrupa - $ H_3 = \ lbrace 1, i \ rbrace $ ponieważ $ (i) ^ {- 1} = -i $ nie znajduje się w $ H_3 $

Częściowo zamówiony zestaw (POSET)

Zbiór częściowo uporządkowany składa się ze zbioru o relacji binarnej, która jest zwrotna, antysymetryczna i przechodnia. „Zestaw częściowo zamówiony” jest w skrócie POSET.

Przykłady

Zbiór liczb rzeczywistych w operacji binarnej mniejszy lub równy $ (\ le) $ jest posetem.

Niech zbiór $ S = \ lbrace 1, 2, 3 \ rbrace $ a operacja to $ \ le $

Relacje będą miały postać $ \ lbrace (1, 1), (2, 2), (3, 3), (1, 2), (1, 3), (2, 3) \ rbrace $

Ta relacja R jest zwrotna jako $ \ lbrace (1, 1), (2, 2), (3, 3) \ rbrace \ in R $

Ta relacja R jest antysymetryczna, jak

$ \ lbrace (1, 2), (1, 3), (2, 3) \ rbrace \ in R \ and \ \ lbrace (1, 2), (1, 3), (2, 3) \ rbrace ∉ R $

Ta relacja R jest również przechodnia jako $ \ lbrace (1,2), (2,3), (1,3) \ rbrace \ w R $.

Dlatego jest to plik poset.
Zbiór wierzchołków skierowanego grafu acyklicznego w ramach operacji „osiągalność” jest posetem.

Diagram Hassego

Diagram Hassego posety jest grafem skierowanym, którego wierzchołki są elementem tej pozycji, a łuki pokrywają pary (x, y) w tej pozycji. Jeśli w posecie $ x <y $, to punkt x pojawia się poniżej punktu y na diagramie Hassego. Jeśli $ x <y <z $ w posecie, to strzałka nie jest pokazana między x i z, ponieważ jest niejawna.

Przykład

Pozet podzbiorów $ \ lbrace 1, 2, 3 \ rbrace = \ lbrace \ emptyset, \ lbrace 1 \ rbrace, \ lbrace 2 \ rbrace, \ lbrace 3 \ rbrace, \ lbrace 1, 2 \ rbrace, \ lbrace 1 , 3 \ rbrace, \ lbrace 2, 3 \ rbrace, \ lbrace 1, 2, 3 \ rbrace \ rbrace $ przedstawia poniższy diagram Hasse'a -

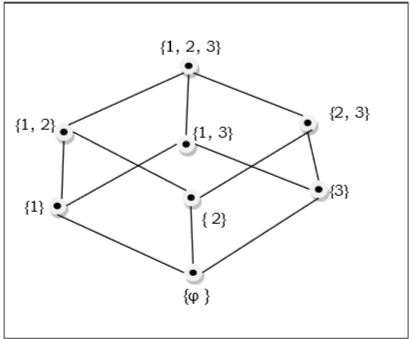
Zestaw uporządkowany liniowo

Zestaw uporządkowany liniowo lub Zestaw uporządkowany łącznie to zestaw częściowego porządku, w którym każda para elementów jest porównywalna. O elementach $ a, b \ w S $ mówi się, że są porównywalne, jeśli trzyma się $ a \ le b $ lub $ b \ le a $. Prawo trychotomii definiuje ten całkowity uporządkowany zbiór. Całkowicie uporządkowany zbiór można zdefiniować jako kratkę dystrybucyjną mającą właściwość $ \ lbrace a \ lor b, a \ land b \ rbrace = \ lbrace a, b \ rbrace $ dla wszystkich wartości a i b w zbiorze S.

Przykład

Zestaw potęg $ \ lbrace a, b \ rbrace $ uporządkowany przez \ subseteq jest zbiorem całkowicie uporządkowanym, ponieważ wszystkie elementy zbioru potęgowego $ P = \ lbrace \ emptyset, \ lbrace a \ rbrace, \ lbrace b \ rbrace, \ lbrace a, b \ rbrace \ rbrace $ są porównywalne.

Przykład niecałkowitego zestawu zamówień

Zbiór $ S = \ lbrace 1, 2, 3, 4, 5, 6 \ rbrace $ w trakcie operacji x dzieli y nie jest całkowitym uporządkowanym zbiorem.

Tutaj, dla wszystkich $ (x, y) \ w S, x | y $ trzeba trzymać, ale nie jest prawdą, że 2 | 3, ponieważ 2 nie dzieli 3 lub 3 nie dzieli 2. Zatem nie jest to uporządkowany zbiór całkowity.

Krata

Krata to poset $ (L, \ le) $, dla którego każda para $ \ lbrace a, b \ rbrace \ in L $ ma najmniejszą górną granicę (oznaczoną przez $ a \ lor b $) i największą dolną granicę ( oznaczony przez $ a \ land b $). LUB $ (\ lbrace a, b \ rbrace) $ jest nazywane złączeniem a i b. GLB $ (\ lbrace a, b \ rbrace) $ nazywa się spotkaniem a i b.

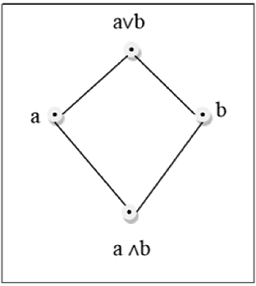
Przykład

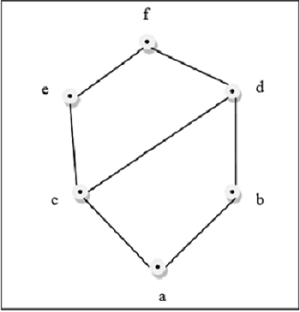
Powyższy rysunek jest kratą, ponieważ dla każdej pary $ \ lbrace a, b \ rbrace \ in L $ istnieje GLB i LUB.

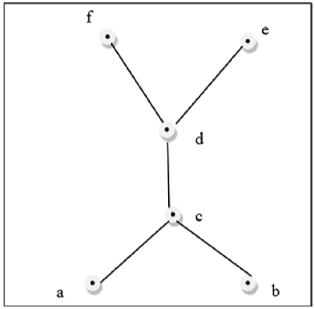
Powyższy rysunek nie jest kratą, ponieważ $ GLB (a, b) $ i $ LUB (e, f) $ nie istnieją.

Niektóre inne kraty są omówione poniżej -

Ograniczona krata

Krata L staje się kratą ograniczoną, jeśli ma największy element 1 i najmniejszy element 0.

Uzupełniona krata

Krata L staje się kratą dopełnioną, jeśli jest kratą ograniczoną i jeśli każdy element w sieci ma dopełnienie. Element x ma dopełnienie x ', jeśli $ \ istnieje x (x \ land x' = 0 i x \ lor x '= 1) $