Uproszczenie funkcji boolowskich
Uproszczenie za pomocą funkcji algebraicznych
W tym podejściu jedno wyrażenie logiczne jest zminimalizowane do równoważnego wyrażenia przez zastosowanie tożsamości boolowskich.
Zadanie 1
Zminimalizuj następujące wyrażenie logiczne za pomocą tożsamości boolowskich -
$$ F (A, B, C) = A'B + BC '+ BC + AB'C' $$
Rozwiązanie
Biorąc pod uwagę, $ F (A, B, C) = A'B + BC '+ BC + AB'C' $
Lub $ F (A, B, C) = A'B + (BC '+ BC') + BC + AB'C '$
[Zgodnie z idempotentnym prawem, BC '= BC' + BC ']
Lub $ F (A, B, C) = A'B + (BC '+ BC) + (BC' + AB'C ') $
Lub $ F (A, B, C) = A'B + B (C '+ C) + C' (B + AB ') $
[Zgodnie z przepisami dystrybucyjnymi]
Lub $ F (A, B, C) = A'B + B.1 + C '(B + A) $
[(C '+ C) = 1 i prawo absorpcji (B + AB') = (B + A)]
Lub $ F (A, B, C) = A'B + B + C '(B + A) $
[B.1 = B]
Lub $ F (A, B, C) = B (A '+ 1) + C' (B + A) $
Lub $ F (A, B, C) = B.1 + C '(B + A) $
[(A '+ 1) = 1]
Lub $ F (A, B, C) = B + C '(B + A) $
[As, B.1 = B]
Lub $ F (A, B, C) = B + BC '+ AC' $
Lub $ F (A, B, C) = B (1 + C ') + AC' $
Lub $ F (A, B, C) = B.1 + AC '$
[As, (1 + C ') = 1]
Lub $ F (A, B, C) = B + AC '$
[As, B.1 = B]
Zatem $ F (A, B, C) = B + AC '$ jest zminimalizowaną formą.
Problem 2
Zminimalizuj następujące wyrażenie logiczne za pomocą tożsamości boolowskich -
$$ F (A, B, C) = (A + B) (A + C) $$
Rozwiązanie
Biorąc pod uwagę, $ F (A, B, C) = (A + B) (A + C) $
Lub $ F (A, B, C) = AA + AC + BA + BC $ [Stosowanie reguły podziału]
Lub $ F (A, B, C) = A + AC + BA + BC $ [Stosowanie prawa idempotentnego]
Lub $ F (A, B, C) = A (1 + C) + BA + BC $ [Stosowanie prawa podziału]
Lub $ F (A, B, C) = A + BA + BC $ [Stosowanie prawa dominacji]
Albo $ F (A, B, C) = (A + 1). A + BC $ [Stosowanie prawa podziału]
Albo $ F (A, B, C) = 1.A + BC $ [Stosowanie prawa dominacji]
Lub $ F (A, B, C) = A + BC $ [Stosowanie prawa dominacji]
Zatem $ F (A, B, C) = A + BC $ to zminimalizowana forma.
Mapy Karnaugha
Mapa Karnaugha (mapa K), wprowadzona przez Maurice'a Karnaughina w 1953 r., Jest siatkową reprezentacją tabeli prawdy, która jest używana do uproszczenia wyrażeń algebry boolowskiej. Mapa Karnaugha ma zero i jeden wpis w różnych pozycjach. Zapewnia grupowanie wyrażeń boolowskich ze wspólnymi czynnikami i eliminuje niechciane zmienne z wyrażenia. Na mapie K przekroczenie pionowej lub poziomej granicy komórki jest zawsze zmianą tylko jednej zmiennej.
Przykład 1
Arbitralna tabela prawdy jest przedstawiona poniżej -
| ZA | b | Operacja B. |
|---|---|---|
| 0 | 0 | w |
| 0 | 1 | x |
| 1 | 0 | y |
| 1 | 1 | z |
Teraz zrobimy k-mapę dla powyższej tabeli prawdy -

Przykład 2
Teraz stworzymy mapę K dla wyrażenia - AB + A'B '
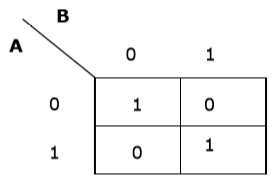
Uproszczenie za pomocą mapy K
K-map używa pewnych reguł do upraszczania wyrażeń boolowskich poprzez łączenie ze sobą sąsiednich komórek w jeden termin. Zasady opisano poniżej -
Rule 1 - Żadnej komórki zawierającej zero nie można grupować.
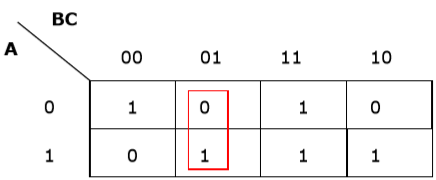
Niewłaściwe grupowanie
Rule 2 - Grupy muszą zawierać 2n komórek (n zaczynając od 1).
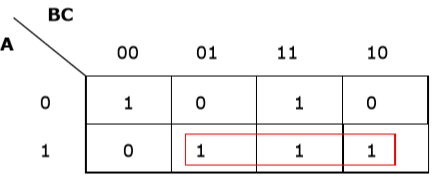
Niewłaściwe grupowanie
Rule 3 - Grupowanie musi być poziome lub pionowe, ale nie może być ukośne.
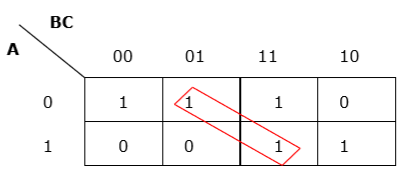
Nieprawidłowe grupowanie po przekątnej
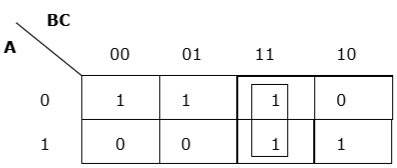
Właściwe grupowanie pionowe
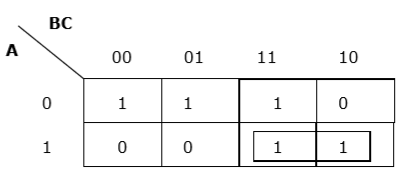
Właściwe grupowanie poziome
Rule 4 - Grupy muszą być uwzględnione w jak największej liczbie.
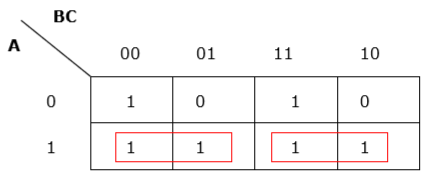
Niewystarczające grupowanie
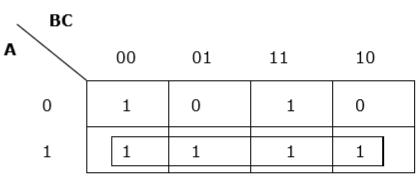
Właściwe grupowanie
Rule 5 - Jeśli 1 z dowolnej komórki nie może być zgrupowany z inną komórką, będzie działać jako grupa.
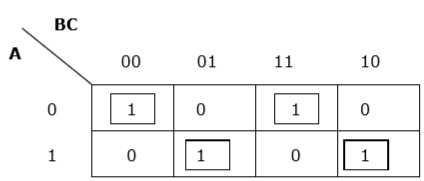
Właściwe grupowanie
Rule 6 - Grupy mogą się nakładać, ale powinno być jak najmniej grup.
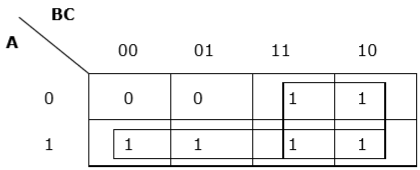
Właściwe grupowanie
Rule 7 - Komórka / komórki znajdujące się najbardziej po lewej stronie można zgrupować z komórką / komórkami położonymi najbardziej po prawej, a komórka / komórki znajdujące się najwyżej można zgrupować z komórką / komórkami położonymi najniżej.
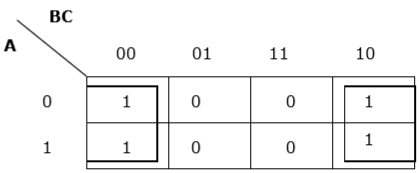
Właściwe grupowanie
Problem
Zminimalizuj następujące wyrażenie logiczne za pomocą K-map -
$$ F (A, B, C) = A'BC + A'BC '+ AB'C' + AB'C $$
Rozwiązanie
Każdy termin jest umieszczany w k-mapie i otrzymujemy:
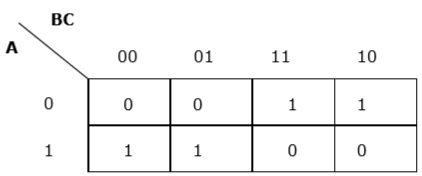
Mapa K dla F (A, B, C)
Teraz pogrupujemy komórki o wartości 1 zgodnie z powyższymi zasadami -
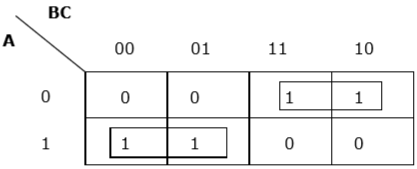
Mapa K dla F (A, B, C)
Mamy dwie grupy, które są określane jako $ A'B $ i $ AB '$. Stąd $ F (A, B, C) = A'B + AB '= A \ oplus B $. To zminimalizowana forma.