Matematyka dyskretna - zbiory

Niemiecki matematyk G. Cantorwprowadził pojęcie zbiorów. Zbiór zdefiniował jako zbiór określonych i rozróżnialnych obiektów wybranych za pomocą pewnych reguł lub opisu.

SetTeoria stanowi podstawę kilku innych dziedzin nauki, takich jak teoria liczenia, relacje, teoria grafów i maszyny skończone. W tym rozdziale omówimy różne aspektySet Theory.

Zestaw - definicja

Zestaw to nieuporządkowana kolekcja różnych elementów. Zestaw można napisać jawnie, wypisując jego elementy za pomocą nawiasu ustalającego. Zmiana kolejności elementów lub powtórzenie dowolnego elementu zestawu nie powoduje żadnych zmian w zestawie.

Kilka przykładów zestawów

Zbiór wszystkich dodatnich liczb całkowitych
Zbiór wszystkich planet Układu Słonecznego
Zestawienie wszystkich stanów w Indiach
Zbiór wszystkich małych liter alfabetu

Reprezentacja zestawu

Zestawy można przedstawić na dwa sposoby -

Lista lub forma tabelaryczna
Ustaw notację konstruktora

Lista lub forma tabelaryczna

Zestaw jest reprezentowany przez wylistowanie wszystkich elementów, które go tworzą. Elementy są ujęte w nawiasy i oddzielone przecinkami.

Example 1 - zestaw samogłosek w alfabecie angielskim, $ A = \ lbrace a, e, i, o, u \ rbrace $

Example 2 - Zbiór liczb nieparzystych mniejszych niż 10, $ B = \ lbrace 1,3,5,7,9 \ rbrace $

Ustaw notację konstruktora

Zestaw jest definiowany przez określenie właściwości, które elementy zestawu mają wspólną. Zbiór jest opisany jako $ A = \ lbrace x: p (x) \ rbrace $

Example 1 - Zbiór $ \ lbrace a, e, i, o, u \ rbrace $ jest zapisywany jako -

$ A = \ lbrace x: \ text {x to samogłoska w alfabecie angielskim} \ rbrace $

Example 2 - Zbiór $ \ lbrace 1,3,5,7,9 \ rbrace $ jest zapisywany jako -

$ B = \ lbrace x: 1 \ le x \ lt 10 \ and \ (x \% 2) \ ne 0 \ rbrace $

Jeśli element x jest członkiem dowolnego zbioru S, jest oznaczony przez $ x \ w S $, a jeśli element y nie należy do zbioru S, jest oznaczany przez $ y \ notw S $.

Example- Jeśli $ S = \ lbrace1, 1,2, 1,7, 2 \ rbrace, 1 \ w S $, ale 1,5 $ \ notin S $

Kilka ważnych zestawów

N - zbiór wszystkich liczb naturalnych = $ \ lbrace1, 2, 3, 4, ..... \ rbrace $

Z - zbiór wszystkich liczb całkowitych = $ \ lbrace ....., -3, -2, -1, 0, 1, 2, 3, ..... \ rbrace $

Z⁺ - zbiór wszystkich dodatnich liczb całkowitych

Q - zbiór wszystkich liczb wymiernych

R - zbiór wszystkich liczb rzeczywistych

W - zbiór wszystkich liczb całkowitych

Liczność zbioru

Liczność zbioru S, oznaczona przez $ | S | $, to liczba elementów zbioru. Liczba jest również nazywana liczbą kardynalną. Jeśli zbiór ma nieskończoną liczbę elementów, jego liczność wynosi $ \ infty $.

Example- $ | \ lbrace 1, 4, 3, 5 \ rbrace | = 4, | \ lbrace 1, 2, 3, 4, 5, \ dots \ rbrace | = \ infty $

Jeśli istnieją dwa zbiory X i Y,

$ | X | = | Y | $ oznacza dwa zbiory X i Y o tej samej liczności. Występuje, gdy liczba elementów w X jest dokładnie równa liczbie elementów w Y. W tym przypadku istnieje funkcja bijektywna „f” od X do Y.
$ | X | \ le | Y | $ oznacza, że liczność zbioru X jest mniejsza lub równa liczności zbioru Y. Występuje, gdy liczba elementów w X jest mniejsza lub równa liczbie Y. Tutaj istnieje funkcja iniekcyjna „f” od X do Y.
$ | X | \ lt | Y | $ oznacza, że liczność zbioru X jest mniejsza niż liczność zbioru Y. Występuje, gdy liczba elementów w X jest mniejsza niż liczba w Y. Tutaj funkcja „f” od X do Y jest funkcją iniekcyjną, ale nie bijektywną.
$ Jeśli \ | X | \ le | Y | $ i $ | X | \ ge | Y | $, a następnie $ | X | = | Y | $. Zbiory X i Y są powszechnie nazywane zbiorami równoważnymi.

Rodzaje zestawów

Zestawy można podzielić na wiele typów. Niektóre z nich są skończone, nieskończone, podzbiór, uniwersalny, właściwy, pojedynczy zbiór itp.

Zbiór skończony

Zbiór zawierający określoną liczbę elementów nazywany jest zbiorem skończonym.

Example- $ S = \ lbrace x \: | \: x \ in N $ i 70 $ \ gt x \ gt 50 \ rbrace $

Nieskończony zestaw

Zbiór zawierający nieskończoną liczbę elementów nazywany jest nieskończonym zbiorem.

Example- $ S = \ lbrace x \: | \: x \ in N $ i $ x \ gt 10 \ rbrace $

Podzbiór

Zbiór X jest podzbiorem zbioru Y (zapisanym jako $ X \ subseteq Y $), jeśli każdy element X jest elementem zbioru Y.

Example 1- Niech, $ X = \ lbrace 1, 2, 3, 4, 5, 6 \ rbrace $ i $ Y = \ lbrace 1, 2 \ rbrace $. Tutaj zbiór Y jest podzbiorem zbioru X, ponieważ wszystkie elementy zbioru Y znajdują się w zbiorze X. Stąd możemy zapisać $ Y \ subseteq X $.

Example 2- Niech, $ X = \ lbrace 1, 2, 3 \ rbrace $ i $ Y = \ lbrace 1, 2, 3 \ rbrace $. Tutaj zbiór Y jest podzbiorem (niewłaściwym podzbiorem) zbioru X, ponieważ wszystkie elementy zbioru Y znajdują się w zbiorze X. Stąd możemy zapisać $ Y \ subseteq X $.

Właściwy podzbiór

Termin „właściwy podzbiór” można zdefiniować jako „podzbiór, ale nie równy”. Zbiór X jest właściwym podzbiorem zbioru Y (zapisanym jako $ X \ podzbiór Y $), jeśli każdy element X jest elementem zbioru Y i $ | X | \ lt | Y | $.

Example- Niech, $ X = \ lbrace 1, 2, 3, 4, 5, 6 \ rbrace $ i $ Y = \ lbrace 1, 2 \ rbrace $. Tutaj ustaw $ Y \ podzbiór X $, ponieważ wszystkie elementy w $ Y $ są również zawarte w $ X $, a $ X $ ma co najmniej jeden element jest większy niż ustawiony $ Y $.

Uniwersalny zestaw

Jest to zbiór wszystkich elementów w określonym kontekście lub aplikacji. Wszystkie zbiory w tym kontekście lub zastosowaniu są zasadniczo podzbiorami tego uniwersalnego zbioru. Zestawy uniwersalne są reprezentowane jako $ U $.

Example- Możemy zdefiniować $ U $ jako zbiór wszystkich zwierząt na ziemi. W tym przypadku zbiór wszystkich ssaków to podzbiór $ U $, zbiór wszystkich ryb to podzbiór $ U $, zbiór wszystkich owadów to podzbiór $ U $ i tak dalej.

Pusty zestaw lub pusty zestaw

Pusty zestaw nie zawiera żadnych elementów. Jest oznaczony przez $ \ emptyset $. Ponieważ liczba elementów w pustym zbiorze jest skończona, pusty zbiór jest zbiorem skończonym. Liczność zestawu pustego lub zestawu zerowego wynosi zero.

Example- $ S = \ lbrace x \: | \: x \ in N $ i $ 7 \ lt x \ lt 8 \ rbrace = \ emptyset $

Zestaw singletonów lub zestaw jednostek

Zestaw singletonów lub zestaw jednostek zawiera tylko jeden element. Zbiór singletonów jest oznaczany przez $ \ lbrace s \ rbrace $.

Example- $ S = \ lbrace x \: | \: x \ in N, \ 7 \ lt x \ lt 9 \ rbrace $ = $ \ lbrace 8 \ rbrace $

Równy zestaw

Jeśli dwa zbiory zawierają te same elementy, mówi się, że są równe.

Example - Jeśli $ A = \ lbrace 1, 2, 6 \ rbrace $ i $ B = \ lbrace 6, 1, 2 \ rbrace $, są równe, ponieważ każdy element zbioru A jest elementem zbioru B i każdym elementem zbioru B jest elementem zbioru A.

Równoważny zestaw

Jeśli liczności dwóch zbiorów są takie same, nazywane są zbiorami równoważnymi.

Example- Jeśli $ A = \ lbrace 1, 2, 6 \ rbrace $ i $ B = \ lbrace $ 16, 17, 22 \ rbrace $, są one równoważne, ponieważ liczność A jest równa liczności B. tj. $ | A | = | B | = 3 $

Nakładający się zestaw

Dwa zestawy, które mają co najmniej jeden wspólny element, nazywane są zestawami nakładającymi się.

W przypadku nakładania się zestawów -

$ n (A \ cup B) = n (A) + n (B) - n (A \ cap B) $
$ n (A \ cup B) = n (A - B) + n (B - A) + n (A \ cap B) $
$ n (A) = n (A - B) + n (A \ cap B) $
$ n (B) = n (B - A) + n (A \ cap B) $

Example- Niech, $ A = \ lbrace 1, 2, 6 \ rbrace $ i $ B = \ lbrace 6, 12, 42 \ rbrace $. Istnieje wspólny element „6”, stąd te zbiory są zbiorami nakładającymi się.

Zestaw rozłączny

Dwa zbiory A i B nazywane są zbiorami rozłącznymi, jeśli nie mają ani jednego wspólnego elementu. Dlatego rozłączne zbiory mają następujące właściwości -

$ n (A \ cap B) = \ emptyset $
$ n (A \ cup B) = n (A) + n (B) $

Example - Niech $ A = \ lbrace 1, 2, 6 \ rbrace $ i $ B = \ lbrace 7, 9, 14 \ rbrace $, nie ma ani jednego wspólnego elementu, stąd te zbiory są nakładającymi się zbiorami.

Diagramy Venna

Diagram Venna, wynaleziony w 1880 roku przez Johna Venna, jest schematem pokazującym wszystkie możliwe relacje logiczne między różnymi zbiorami matematycznymi.

Examples

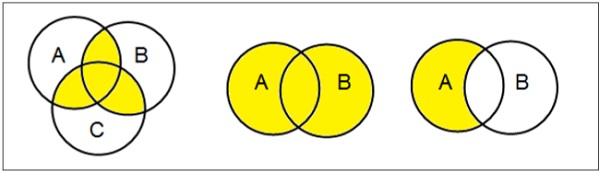
Operacje na zbiorach

Operacje na zbiorach obejmują sumę zbioru, przecięcie zbioru, różnicę zbioru, dopełnienie zbioru i iloczyn kartezjański.

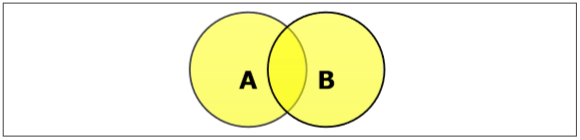
Ustaw Union

Suma zbiorów A i B (oznaczona przez $ A \ cup B $) to zbiór elementów znajdujących się w A, w B lub w A i B. Stąd $ A \ cup B = \ lbrace x \: | \: x \ in A \ OR \ x \ in B \ rbrace $.

Example- Jeśli $ A = \ lbrace 10, 11, 12, 13 \ rbrace $ i B = $ \ lbrace 13, 14, 15 \ rbrace $, to $ A \ cup B = \ lbrace 10, 11, 12, 13, 14 , 15 \ rbrace $. (Wspólny element występuje tylko raz)

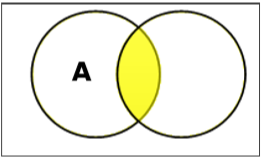
Ustaw przecięcie

Punkt przecięcia zbiorów A i B (oznaczonych przez $ A \ cap B $) to zbiór elementów znajdujących się zarówno w A, jak i B. Stąd $ A \ cap B = \ lbrace x \: | \: x \ in A \ AND \ x \ in B \ rbrace $.

Example - Jeśli $ A = \ lbrace 11, 12, 13 \ rbrace $ i $ B = \ lbrace 13, 14, 15 \ rbrace $, to $ A \ cap B = \ lbrace 13 \ rbrace $.

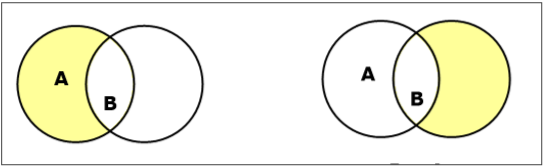
Ustaw różnicę / względne dopełnienie

Różnica zbiorów A i B (oznaczona przez $ A - B $) to zbiór elementów, które są tylko w A, ale nie w B. Stąd $ A - B = \ lbrace x \: | \: x \ in A \ AND \ x \ notin B \ rbrace $.

Example- Jeśli $ A = \ lbrace 10, 11, 12, 13 \ rbrace $ i $ B = \ lbrace 13, 14, 15 \ rbrace $, to $ (A - B) = \ lbrace 10, 11, 12 \ rbrace $ i $ (B - A) = \ lbrace 14, 15 \ rbrace $. Tutaj widzimy $ (A - B) \ ne (B - A) $

Uzupełnienie zestawu

Uzupełnieniem zbioru A (oznaczonego przez $ A '$) jest zbiór elementów, których nie ma w zbiorze A. Stąd $ A' = \ lbrace x | x \ notin A \ rbrace $.

Dokładniej, $ A '= (U - A) $, gdzie $ U $ to uniwersalny zestaw zawierający wszystkie obiekty.

Example- Jeśli $ A = \ lbrace x \: | \: x \ \: {należy \: do \: set \: of \: odd \: integers} \ rbrace $, a następnie $ A '= \ lbrace y \: | \: y \ \: {nie \: nie \: należy \: do \: set \: of \: odd \: integers} \ rbrace $

Iloczyn kartezjański / Iloczyn poprzeczny

Iloczyn kartezjański n liczby zbiorów $ A_1, A_2, \ dots A_n $ oznaczonych jako $ A_1 \ times A_2 \ dots \ times A_n $ można zdefiniować jako wszystkie możliwe uporządkowane pary $ (x_1, x_2, \ dots x_n) $ gdzie $ x_1 \ in A_1, x_2 \ in A_2, \ dots x_n \ in A_n $

Example - Jeśli weźmiemy dwa zbiory $ A = \ lbrace a, b \ rbrace $ i $ B = \ lbrace 1, 2 \ rbrace $,

Iloczyn kartezjański A i B jest zapisywany jako - $ A \ razy B = \ lbrace (a, 1), (a, 2), (b, 1), (b, 2) \ rbrace $

Iloczyn kartezjański B i A jest zapisywany jako - $ B \ razy A = \ lbrace (1, a), (1, b), (2, a), (2, b) \ rbrace $

Zestaw zasilający

Zbiór potęgowy zbioru S to zbiór wszystkich podzbiorów zbioru S, w tym zbiór pusty. Liczność zbioru potęg zbioru S o liczności n wynosi 2 $ n $. Zestaw mocy oznaczony jest jako $ P (S) $.

Example −

Dla zbioru $ S = \ lbrace a, b, c, d \ rbrace $ obliczmy podzbiory -

Podzbiory z 0 elementami - $ \ lbrace \ emptyset \ rbrace $ (pusty zbiór)
Podzbiory z 1 elementem - $ \ lbrace a \ rbrace, \ lbrace b \ rbrace, \ lbrace c \ rbrace, \ lbrace d \ rbrace $
Podzbiory z 2 elementami - $ \ lbrace a, b \ rbrace, \ lbrace a, c \ rbrace, \ lbrace a, d \ rbrace, \ lbrace b, c \ rbrace, \ lbrace b, d \ rbrace, \ lbrace c, d \ rbrace $
Podzbiory z 3 elementami - $ \ lbrace a, b, c \ rbrace, \ lbrace a, b, d \ rbrace, \ lbrace a, c, d \ rbrace, \ lbrace b, c, d \ rbrace $
Podzbiory z 4 elementami - $ \ lbrace a, b, c, d \ rbrace $

Stąd $ P (S) = $

$ \ lbrace \ quad \ lbrace \ emptyset \ rbrace, \ lbrace a \ rbrace, \ lbrace b \ rbrace, \ lbrace c \ rbrace, \ lbrace d \ rbrace, \ lbrace a, b \ rbrace, \ lbrace a, c \ rbrace, \ lbrace a, d \ rbrace, \ lbrace b, c \ rbrace, \ lbrace b, d \ rbrace, \ lbrace c, d \ rbrace, \ lbrace a, b, c \ rbrace, \ lbrace a, b, d \ rbrace, \ lbrace a, c, d \ rbrace, \ lbrace b, c, d \ rbrace, \ lbrace a, b, c, d \ rbrace \ quad \ rbrace $

$ | P (S) | = 2 ^ 4 = 16 $

Note - Moc zestawu pustego jest również zestawem pustym.

$ | P (\ lbrace \ emptyset \ rbrace) | = 2 ^ 0 = 1 $

Partycjonowanie zbioru

Podział zbioru, powiedzmy S , to zbiór n rozłącznych podzbiorów, powiedzmy $ P_1, P_2, \ dots P_n $, który spełnia następujące trzy warunki -

$ P_i $ nie zawiera pustego zestawu.

$ \ lbrack P_i \ ne \ lbrace \ emptyset \ rbrace \ for \ all \ 0 \ lt i \ le n \ rbrack $
Suma podzbiorów musi być równa całemu oryginalnemu zestawowi.

$ \ lbrack P_1 \ cup P_2 \ cup \ dots \ cup P_n = S \ rbrack $
Przecięcie dowolnych dwóch różnych zestawów jest puste.

$ \ lbrack P_a \ cap P_b = \ lbrace \ emptyset \ rbrace, \ for \ a \ ne b \ gdzie \ n \ ge a, \: b \ ge 0 \ rbrack $

Example

Niech $ S = \ lbrace a, b, c, d, e, f, g, h \ rbrace $

Prawdopodobne partycjonowanie to $ \ lbrace a \ rbrace, \ lbrace b, c, d \ rbrace, \ lbrace e, f, g, h \ rbrace $

Innym prawdopodobnym podziałem jest $ \ lbrace a, b \ rbrace, \ lbrace c, d \ rbrace, \ lbrace e, f, g, h \ rbrace $