Matematyka dyskretna - relacje
Ilekroć dyskutuje się o zbiorach, następną rzeczą, która się pojawia, jest relacja między elementami zbiorów. Relations może istnieć między obiektami tego samego zestawu lub między obiektami dwóch lub więcej zestawów.
Definicja i właściwości
Relacja binarna R ze zbioru x do y (zapisana jako $ xRy $ lub $ R (x, y) $) jest podzbiorem iloczynu kartezjańskiego $ x \ razy y $. Jeśli uporządkowana para G jest odwrócona, relacja również się zmienia.
Ogólnie rzecz biorąc, relacja n-ary R między zbiorami $ A_1, \ dots, \ i \ A_n $ jest podzbiorem iloczynu n-arowego $ A_1 \ times \ dots \ times A_n $. Minimalna liczność relacji R wynosi zero, a maksymalna w tym przypadku to $ n ^ 2 $.
Relacja binarna R na pojedynczym zbiorze A jest podzbiorem $ A \ razy A $.
Dla dwóch różnych zbiorów, A i B, o liczności odpowiednio m i n , maksymalna liczność relacji R od A do B wynosi mn .
Dziedzina i zakres
Jeśli istnieją dwa zbiory A i B, a relacja R ma parę porządkową (x, y), to -
Plik domainR, Dom (R), to zbiór $ \ lbrace x \: | \: (x, y) \ in R \: for \: some \: y \: in \: B \ rbrace $
Plik range z R, Ran (R), to zbiór $ \ lbrace y \: | \: (x, y) \ in R \: for \: some \: x \: in \: A \ rbrace $
Przykłady
Niech, $ A = \ lbrace 1, 2, 9 \ rbrace $ i $ B = \ lbrace 1, 3, 7 \ rbrace $
Przypadek 1 - Jeśli relacja R jest `` równa '', to $ R = \ lbrace (1, 1), (3, 3) \ rbrace $
Dom (R) = $ \ lbrace 1, 3 \ rbrace, Ran (R) = \ lbrace 1, 3 \ rbrace $
Przypadek 2 - Jeśli relacja R jest 'mniejsza niż', to $ R = \ lbrace (1, 3), (1, 7), (2, 3), (2, 7) \ rbrace $
Dom (R) = $ \ lbrace 1, 2 \ rbrace, Ran (R) = \ lbrace 3, 7 \ rbrace $
Przypadek 3 - Jeśli relacja R jest 'większa niż', to $ R = \ lbrace (2, 1), (9, 1), (9, 3), (9, 7) \ rbrace $
Dom (R) = $ \ lbrace 2, 9 \ rbrace, Ran (R) = \ lbrace 1, 3, 7 \ rbrace $
Reprezentacja relacji za pomocą wykresu
Relację można przedstawić za pomocą skierowanego wykresu.
Liczba wierzchołków na grafie jest równa liczbie elementów w zbiorze, z którego została zdefiniowana relacja. Dla każdej uporządkowanej pary (x, y) w relacji R będzie skierowana krawędź od wierzchołka „x” do wierzchołka „y”. Jeśli istnieje uporządkowana para (x, x), na wierzchołku „x” powstanie pętla własna.
Załóżmy, że istnieje relacja $ R = \ lbrace (1, 1), (1,2), (3, 2) \ rbrace $ na zbiorze $ S = \ lbrace 1, 2, 3 \ rbrace $, może to być reprezentowane przez następujący wykres -
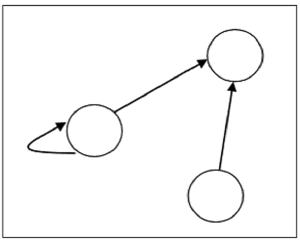
Rodzaje relacji
Plik Empty Relation między zestawami X i Y, lub na E, jest pusty zbiór $ \ emptyset $
Plik Full Relation między zbiorami X i Y to zbiór $ X \ razy Y $
Plik Identity Relationna zbiorze X jest zbiór $ \ lbrace (x, x) | x \ in X \ rbrace $
Relacja odwrotna R 'relacji R jest zdefiniowana jako - $ R' = \ lbrace (b, a) | (a, b) \ in R \ rbrace $
Example - Jeśli $ R = \ lbrace (1, 2), (2, 3) \ rbrace $, to $ R '$ będzie $ \ lbrace (2, 1), (3, 2) \ rbrace $
Wywoływana jest relacja R na zbiorze A. Reflexive jeśli $ \ forall a \ in A $ jest powiązane z a (aRa trzyma)
Example - Relacja $ R = \ lbrace (a, a), (b, b) \ rbrace $ na zbiorze $ X = \ lbrace a, b \ rbrace $ jest zwrotna.
Wywoływana jest relacja R na zbiorze A. Irreflexive jeśli żadne $ a \ w A $ nie jest powiązane z a (aRa nie trzyma).
Example - Relacja $ R = \ lbrace (a, b), (b, a) \ rbrace $ na zbiorze $ X = \ lbrace a, b \ rbrace $ jest nierefleksyjna.
Wywoływana jest relacja R na zbiorze A. Symmetric jeśli $ xRy $ oznacza $ yRx $, $ \ forall x \ in A $ i $ \ forall y \ in A $.
Example - Relacja $ R = \ lbrace (1, 2), (2, 1), (3, 2), (2, 3) \ rbrace $ na zbiorze $ A = \ lbrace 1, 2, 3 \ rbrace $ jest symetryczny.
Wywoływana jest relacja R na zbiorze A. Anti-Symmetric jeśli $ xRy $ i $ yRx $ oznacza $ x = y \: \ forall x \ in A $ i $ \ forall y \ in A $.
Example - Relacja $ R = \ lbrace (x, y) \ to N | \: x \ leq y \ rbrace $ jest anty-symetryczna, ponieważ $ x \ leq y $ i $ y \ leq x $ implikuje $ x = y $ .
Wywoływana jest relacja R na zbiorze A. Transitive jeśli $ xRy $ i $ yRz $ implikuje $ xRz, \ forall x, y, z \ w A $.
Example - Relacja $ R = \ lbrace (1, 2), (2, 3), (1, 3) \ rbrace $ na zbiorze $ A = \ lbrace 1, 2, 3 \ rbrace $ jest przechodnia.
Relacja to Equivalence Relation jeśli jest zwrotny, symetryczny i przechodni.
Example - Relacja $ R = \ lbrace (1, 1), (2, 2), (3, 3), (1, 2), (2,1), (2,3), (3,2), (1,3), (3,1) \ rbrace $ na zbiorze $ A = \ lbrace 1, 2, 3 \ rbrace $ jest relacją równoważności, ponieważ jest zwrotna, symetryczna i przechodnia.