Matematyka dyskretna - Drzewa spinające
Drzewo rozpinające połączonego, niekierowanego grafu $ G $ jest drzewem, które zawiera co najmniej wszystkie wierzchołki $ G $. Wykres może mieć wiele drzew rozpinających.
Przykład
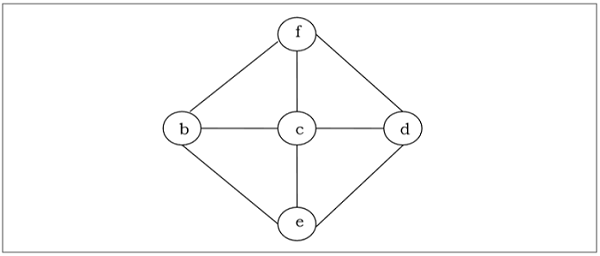
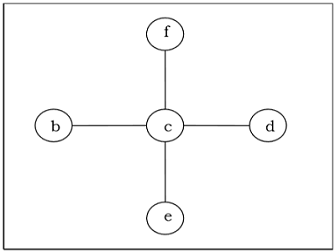
Minimalne drzewo rozpinające
Drzewo opinające z przypisaną wagą mniejszą lub równą wadze każdego możliwego drzewa opinającego ważonego, połączonego i nieukierunkowanego wykresu $ G $, nazywane jest minimalnym drzewem opinającym (MST). Waga drzewa opinającego to suma wszystkich wag przypisanych do każdej krawędzi drzewa opinającego.
Przykład
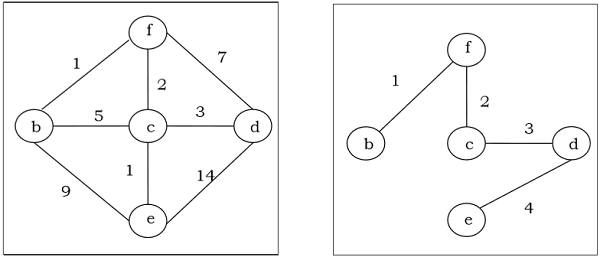
Algorytm Kruskala
Algorytm Kruskala to zachłanny algorytm, który znajduje minimalne drzewo rozpinające dla połączonego wykresu ważonego. Znajduje drzewo tego wykresu, które zawiera każdy wierzchołek, a całkowita waga wszystkich krawędzi w drzewie jest mniejsza lub równa każdemu możliwemu drzewu rozpinającemu.
Algorytm
Step 1 - Ułóż wszystkie krawędzie danego wykresu $ G (V, E) $ w porządku rosnącym zgodnie z ich wagą krawędzi.
Step 2 - Wybierz najmniejszą ważoną krawędź z wykresu i sprawdź, czy tworzy cykl z utworzonym do tej pory drzewem rozpinającym.
Step 3 - Jeśli nie ma cyklu, dołącz tę krawędź do drzewa opinającego, w przeciwnym razie odrzuć ją.
Step 4 - Powtarzaj krok 2 i krok 3, aż $ (V-1) $ liczba krawędzi pozostanie w drzewie opinającym.
Problem
Załóżmy, że chcemy znaleźć minimalne drzewo rozpinające dla następującego wykresu G przy użyciu algorytmu Kruskala.
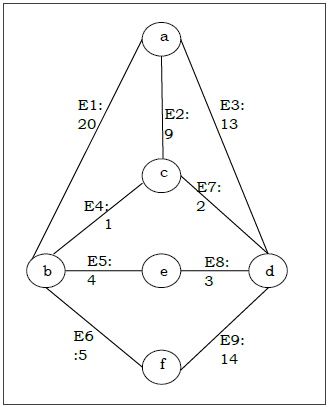
Solution
Z powyższego wykresu konstruujemy następującą tabelę -
| Nr krawędzi | Para wierzchołków | Grubość krawędzi |
|---|---|---|
| E1 | (a, b) | 20 |
| E2 | (a, c) | 9 |
| E3 | (a, d) | 13 |
| E 4 | (pne) | 1 |
| E5 | (być) | 4 |
| E6 | (b, f) | 5 |
| E7 | (Płyta CD) | 2 |
| E8 | (d, e) | 3 |
| E9 | (d, f) | 14 |
Teraz przestawimy tabelę w porządku rosnącym ze względu na wagę krawędzi -
| Nr krawędzi | Para wierzchołków | Grubość krawędzi |
|---|---|---|
| E 4 | (pne) | 1 |
| E7 | (Płyta CD) | 2 |
| E8 | (d, e) | 3 |
| E5 | (być) | 4 |
| E6 | (b, f) | 5 |
| E2 | (a, c) | 9 |
| E3 | (a, d) | 13 |
| E9 | (d, f) | 14 |
| E1 | (a, b) | 20 |
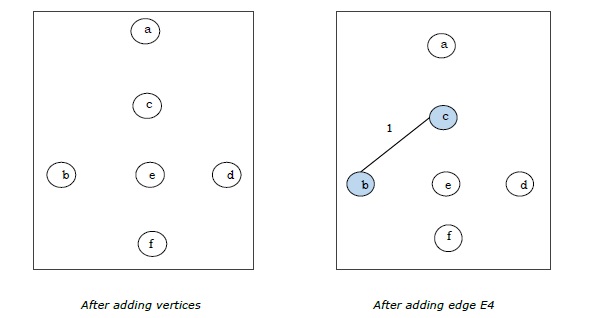
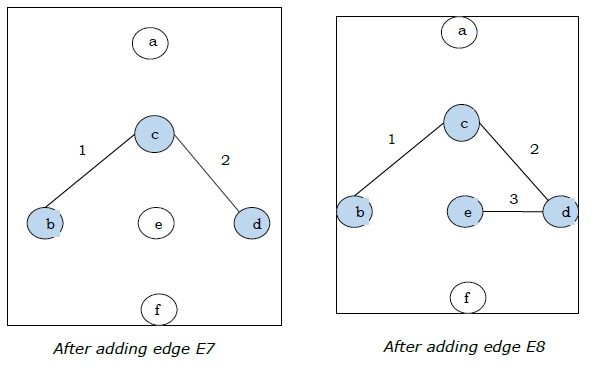
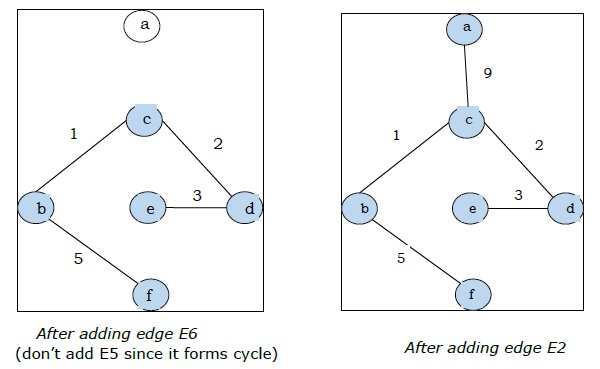
Ponieważ na ostatnim rysunku mamy wszystkie 5 krawędzi, zatrzymujemy algorytm i jest to minimalne drzewo rozpinające, a jego całkowita waga wynosi $ (1 + 2 + 3 + 5 + 9) = 20 $.
Algorytm Prima
Algorytm Prima, odkryty w 1930 roku przez matematyków, Vojtecha Jarnika i Roberta C. Prima, to zachłanny algorytm, który znajduje minimalne drzewo rozpinające dla połączonego grafu ważonego. Znajduje drzewo tego wykresu, które zawiera każdy wierzchołek, a całkowita waga wszystkich krawędzi w drzewie jest mniejsza lub równa każdemu możliwemu drzewu rozpinającemu. Algorytm Prima jest szybszy na gęstych grafach.
Algorytm
Zainicjuj minimalne drzewo opinające jednym wierzchołkiem, wybranym losowo z wykresu.
Powtarzaj kroki 3 i 4, aż wszystkie wierzchołki zostaną uwzględnione w drzewie.
Wybierz krawędź, która łączy drzewo z wierzchołkiem jeszcze nie znajdującym się w drzewie, tak aby waga krawędzi była minimalna, a włączenie krawędzi nie tworzyło cyklu.
Dodaj wybraną krawędź i wierzchołek, który łączy z drzewem.
Problem
Załóżmy, że chcemy znaleźć minimalne drzewo rozpinające dla następującego wykresu G za pomocą algorytmu Prim.
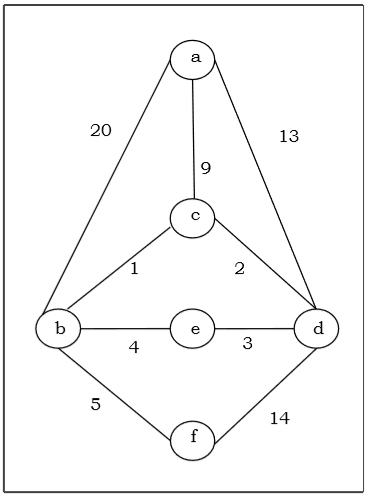
Solution
Tutaj zaczynamy od wierzchołka „a” i kontynuujemy.
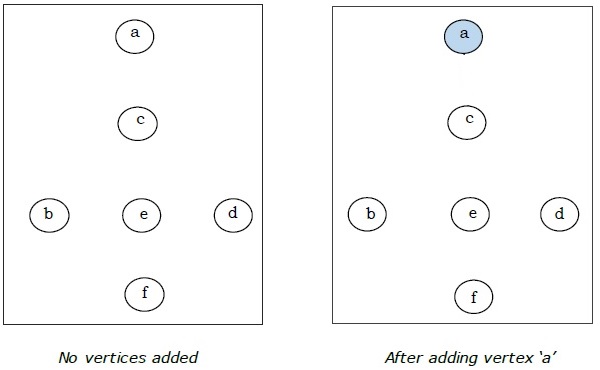
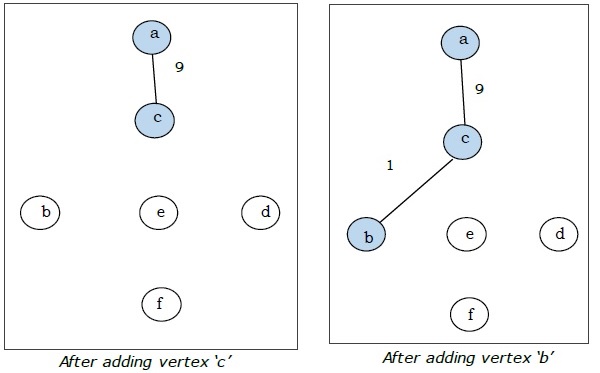
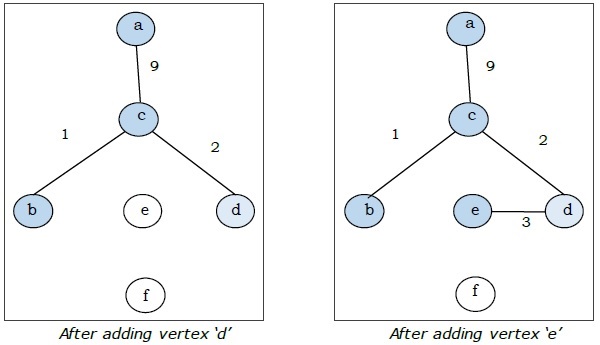
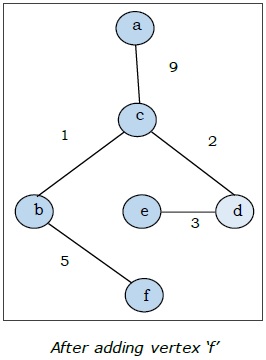
To jest minimalne drzewo rozpinające, a jego całkowita waga wynosi $ (1 + 2 + 3 + 5 + 9) = 20 $.