TensorFlow - regresja liniowa

W tym rozdziale skupimy się na podstawowym przykładzie implementacji regresji liniowej przy użyciu TensorFlow. Regresja logistyczna lub regresja liniowa to nadzorowane podejście uczenia maszynowego do klasyfikacji dyskretnych kategorii porządku. Naszym celem w tym rozdziale jest zbudowanie modelu, za pomocą którego użytkownik może przewidzieć związek między zmiennymi predykcyjnymi a jedną lub większą liczbą zmiennych niezależnych.

Zależność między tymi dwiema zmiennymi jest uważana za liniową. Jeśli y jest zmienną zależną, a x jest uważane za zmienną niezależną, wówczas zależność regresji liniowej dwóch zmiennych będzie wyglądać jak następujące równanie -

Y = Ax+b

Zaprojektujemy algorytm regresji liniowej. Pozwoli nam to zrozumieć dwa ważne pojęcia -

Funkcja kosztu
Algorytmy zejścia gradientu

Schematyczne przedstawienie regresji liniowej jest wymienione poniżej -

Graficzny widok równania regresji liniowej przedstawiono poniżej -

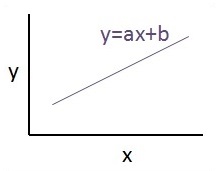
Etapy projektowania algorytmu regresji liniowej

Dowiemy się teraz o krokach, które pomogą w zaprojektowaniu algorytmu regresji liniowej.

Krok 1

Ważne jest, aby zaimportować niezbędne moduły do wykreślenia modułu regresji liniowej. Rozpoczynamy import biblioteki Pythona NumPy i Matplotlib.

import numpy as np 
import matplotlib.pyplot as plt

Krok 2

Określ liczbę współczynników potrzebnych do regresji logistycznej.

number_of_points = 500 
x_point = [] 
y_point = [] 
a = 0.22 
b = 0.78

Krok 3

Powtórz zmienne, aby wygenerować 300 losowych punktów wokół równania regresji -

Y = 0,22x + 0,78

for i in range(number_of_points): 
   x = np.random.normal(0.0,0.5) 
   y = a*x + b +np.random.normal(0.0,0.1) x_point.append([x]) 
   y_point.append([y])

Krok 4

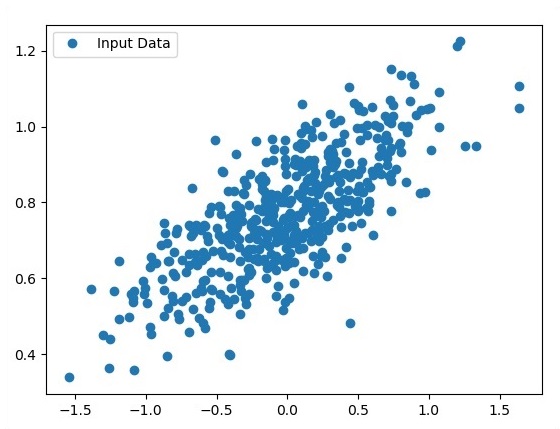
Wyświetl wygenerowane punkty za pomocą Matplotlib.

fplt.plot(x_point,y_point, 'o', label = 'Input Data') plt.legend() plt.show()

Pełny kod regresji logistycznej jest następujący -

import numpy as np 
import matplotlib.pyplot as plt 

number_of_points = 500 
x_point = [] 
y_point = [] 
a = 0.22 
b = 0.78 

for i in range(number_of_points): 
   x = np.random.normal(0.0,0.5) 
   y = a*x + b +np.random.normal(0.0,0.1) x_point.append([x]) 
   y_point.append([y]) 
   
plt.plot(x_point,y_point, 'o', label = 'Input Data') plt.legend() 
plt.show()

Liczba punktów, które są brane za dane wejściowe, jest traktowana jako dane wejściowe.