TensorFlow - podstawy matematyczne
Przed utworzeniem podstawowej aplikacji w TensorFlow ważne jest zrozumienie pojęć matematycznych potrzebnych dla TensorFlow. Matematyka jest uważana za serce każdego algorytmu uczenia maszynowego. To za pomocą podstawowych koncepcji matematyki definiuje się rozwiązanie dla określonego algorytmu uczenia maszynowego.
Wektor
Tablica liczb, która jest ciągła lub dyskretna, jest definiowana jako wektor. Algorytmy uczenia maszynowego radzą sobie z wektorami o stałej długości w celu lepszego generowania wyników.
Algorytmy uczenia maszynowego radzą sobie z wielowymiarowymi danymi, więc wektory odgrywają kluczową rolę.

Graficzne przedstawienie modelu wektorowego jest pokazane poniżej -
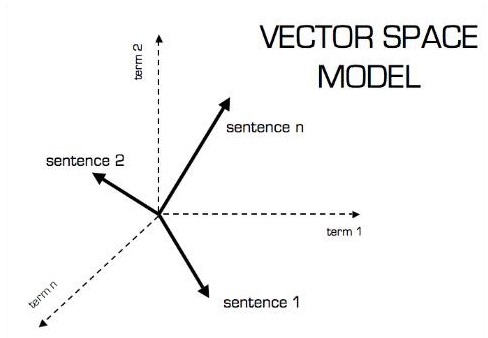
Skalarny
Skalar można zdefiniować jako wektor jednowymiarowy. Skalary to takie, które obejmują tylko wielkość, a nie kierunek. W przypadku skalarów interesuje nas tylko wielkość.
Przykładowe wartości skalarne obejmują parametry wagi i wzrostu dzieci.
Matryca
Macierz można zdefiniować jako tablice wielowymiarowe, które są ułożone w formacie wierszy i kolumn. Rozmiar macierzy jest określany przez długość wiersza i długość kolumny. Poniższy rysunek przedstawia reprezentację dowolnej określonej macierzy.
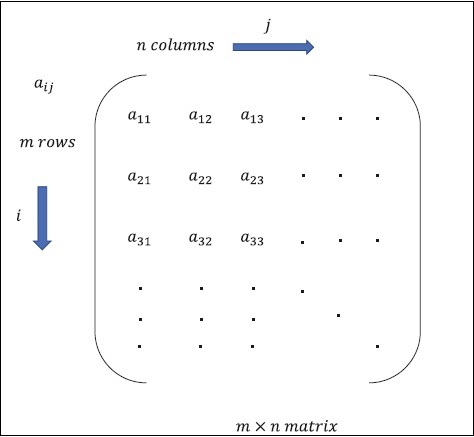
Rozważmy macierz z wierszami „m” i kolumnami „n”, jak wspomniano powyżej, reprezentacja macierzy będzie określona jako „macierz m * n”, która również określała długość macierzy.
Obliczenia matematyczne
W tej sekcji dowiemy się o różnych obliczeniach matematycznych w TensorFlow.
Dodawanie macierzy
Dodanie dwóch lub więcej macierzy jest możliwe, jeśli macierze mają ten sam wymiar. Dodanie oznacza dodanie każdego elementu zgodnie z podaną pozycją.
Rozważ następujący przykład, aby zrozumieć, jak działa dodawanie macierzy -
$$ Przykład: A = \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} B = \ begin {bmatrix} 5 & 6 \\ 7 & 8 \ end {bmatrix} \: then \: A + B = \ begin {bmatrix} 1 + 5 i 2 + 6 \\ 3 + 7 i 4 + 8 \ end {bmatrix} = \ begin {bmatrix} 6 i 8 \\ 10 i 12 \ end {bmatrix} $$
Odejmowanie macierzy
Odejmowanie macierzy działa w podobny sposób, jak dodawanie dwóch macierzy. Użytkownik może odjąć dwie macierze pod warunkiem, że wymiary są równe.
$$ Przykład: A- \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} B- \ begin {bmatrix} 5 & 6 \\ 7 & 8 \ end {bmatrix} \: then \: AB - \ begin {bmatrix} 1-5 & 2-6 \\ 3-7 & 4-8 \ end {bmatrix} - \ begin {bmatrix} -4 & -4 \\ - 4 & -4 \ end {bmatrix} $$
Mnożenie macierzy
Aby dwie macierze A m * n i B p * q były mnożone, n powinno być równe p. Otrzymana macierz to -
C m * q
$$ A = \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} B = \ begin {bmatrix} 5 & 6 \\ 7 & 8 \ end {bmatrix} $$
$$ c_ {11} = \ begin {bmatrix} 1 & 2 \ end {bmatrix} \ begin {bmatrix} 5 \\ 7 \ end {bmatrix} = 1 \ times5 + 2 \ times7 = 19 \: c_ {12} = \ begin {bmatrix} 1 & 2 \ end {bmatrix} \ begin {bmatrix} 6 \\ 8 \ end {bmatrix} = 1 \ times6 + 2 \ times8 = 22 $$
$$ c_ {21} = \ begin {bmatrix} 3 & 4 \ end {bmatrix} \ begin {bmatrix} 5 \\ 7 \ end {bmatrix} = 3 \ times5 + 4 \ times7 = 43 \: c_ {22} = \ begin {bmatrix} 3 & 4 \ end {bmatrix} \ begin {bmatrix} 6 \\ 8 \ end {bmatrix} = 3 \ times6 + 4 \ times8 = 50 $$
$$ C = \ begin {bmatrix} c_ {11} & c_ {12} \\ c_ {21} & c_ {22} \ end {bmatrix} = \ begin {bmatrix} 19 i 22 \\ 43 i 50 \ end {bmatrix} $$
Transpozycja macierzy
Transpozycja macierzy A, m * n jest ogólnie reprezentowana przez AT (transpozycja) n * m i jest uzyskiwana przez transpozycję wektorów kolumnowych jako wektorów wierszowych.
$$ Przykład: A = \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} \: then \: A ^ {T} \ begin {bmatrix} 1 & 3 \\ 2 & 4 \ end { bmatrix} $$
Iloczyn skalarny wektorów
Dowolny wektor wymiaru n można przedstawić jako macierz v = R ^ n * 1.
$$ v_ {1} = \ begin {bmatrix} v_ {11} \\ v_ {12} \\\ cdot \\\ cdot \\\ cdot \\ v_ {1n} \ end {bmatrix} v_ {2} = \ begin {bmatrix} v_ {21} \\ v_ {22} \\\ cdot \\\ cdot \\\ cdot \\ v_ {2n} \ end {bmatrix} $$
Iloczyn skalarny dwóch wektorów jest sumą iloczynu odpowiednich składników - Składników wzdłuż tego samego wymiaru i można go wyrazić jako
$$ v_ {1} \ cdot v_ {2} = v_1 ^ Tv_ {2} = v_2 ^ Tv_ {1} = v_ {11} v_ {21} + v_ {12} v_ {22} + \ cdot \ cdot + v_ {1n} v_ {2n} = \ displaystyle \ sum \ limit_ {k = 1} ^ n v_ {1k} v_ {2k} $$
Przykład iloczynu skalarnego wektorów podano poniżej -
$$ Przykład: v_ {1} = \ begin {bmatrix} 1 \\ 2 \\ 3 \ end {bmatrix} v_ {2} = \ begin {bmatrix} 3 \\ 5 \\ - 1 \ end {bmatrix} v_ {1} \ cdot v_ {2} = v_1 ^ Tv_ {2} = 1 \ times3 + 2 \ times5-3 \ times1 = 10 $$