TensorFlow - Perceptron jednowarstwowy

Aby zrozumieć perceptron jednowarstwowy, ważne jest, aby zrozumieć sztuczne sieci neuronowe (SSN). Sztuczne sieci neuronowe to system przetwarzania informacji, którego mechanizm jest inspirowany funkcjonalnością biologicznych obwodów neuronowych. Sztuczna sieć neuronowa zawiera wiele połączonych ze sobą jednostek przetwarzających. Poniżej znajduje się schematyczne przedstawienie sztucznej sieci neuronowej -

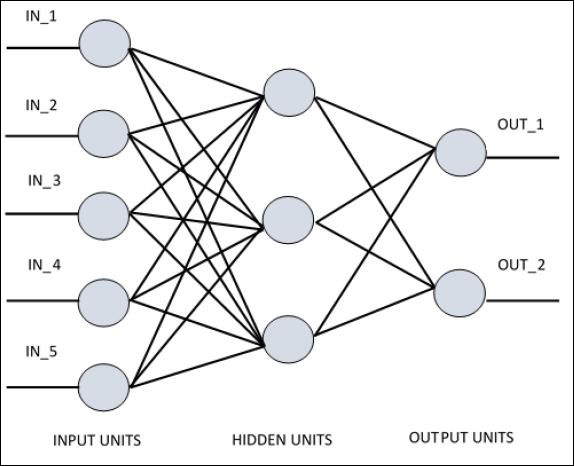
Diagram pokazuje, że ukryte jednostki komunikują się z warstwą zewnętrzną. Podczas gdy jednostki wejściowe i wyjściowe komunikują się tylko przez ukrytą warstwę sieci.

Wzorzec połączenia z węzłami, całkowita liczba warstw i poziom węzłów między wejściami i wyjściami wraz z liczbą neuronów na warstwę określają architekturę sieci neuronowej.

Istnieją dwa rodzaje architektury. Te typy koncentrują się na funkcjonalności sztucznych sieci neuronowych w następujący sposób -

• Perceptron jednowarstwowy
• Perceptron wielowarstwowy

Perceptron jednowarstwowy

Perceptron jednowarstwowy jest pierwszym zaproponowanym modelem neuronowym. Zawartość lokalnej pamięci neuronu składa się z wektora wag. Obliczenia perceptronu jednowarstwowego przeprowadza się poprzez obliczenie sumy wektora wejściowego, z których każdy ma wartość pomnożoną przez odpowiedni element wektora wag. Wartość wyświetlana na wyjściu będzie wartością wejściową funkcji aktywacji.

Skoncentrujmy się na implementacji perceptronu jednowarstwowego do problemu klasyfikacji obrazu przy użyciu TensorFlow. Najlepszym przykładem ilustrującym perceptron jednowarstwowy jest przedstawienie „regresji logistycznej”.

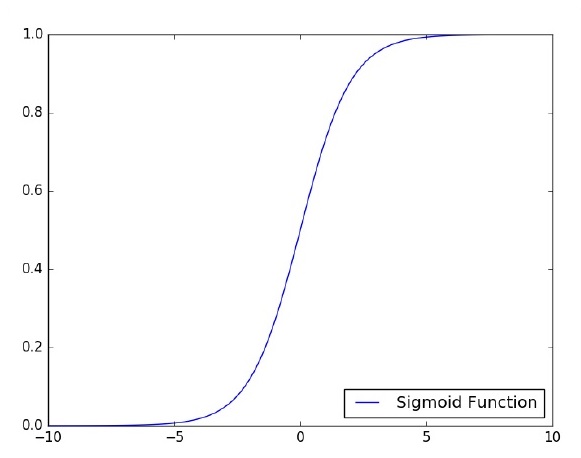
Rozważmy teraz następujące podstawowe kroki treningu regresji logistycznej -

• Na początku treningu wagi są inicjowane losowymi wartościami.

• Dla każdego elementu zbioru uczącego błąd jest obliczany z różnicy między pożądanym wyjściem a rzeczywistym wyjściem. Obliczony błąd służy do korygowania wag.

• Proces jest powtarzany, aż błąd popełniony na całym zbiorze uczącym nie będzie mniejszy niż określony próg, aż do osiągnięcia maksymalnej liczby iteracji.

Pełny kod do oceny regresji logistycznej jest wymieniony poniżej -

# Import MINST data 
from tensorflow.examples.tutorials.mnist import input_data 
mnist = input_data.read_data_sets("/tmp/data/", one_hot = True) 

import tensorflow as tf 
import matplotlib.pyplot as plt 

# Parameters 
learning_rate = 0.01 
training_epochs = 25 
batch_size = 100 
display_step = 1 

# tf Graph Input 
x = tf.placeholder("float", [None, 784]) # mnist data image of shape 28*28 = 784 
y = tf.placeholder("float", [None, 10]) # 0-9 digits recognition => 10 classes 

# Create model 
# Set model weights 
W = tf.Variable(tf.zeros([784, 10])) 
b = tf.Variable(tf.zeros([10])) 

# Construct model 
activation = tf.nn.softmax(tf.matmul(x, W) + b) # Softmax 

# Minimize error using cross entropy 
cross_entropy = y*tf.log(activation) 
cost = tf.reduce_mean\ (-tf.reduce_sum\ (cross_entropy,reduction_indices = 1)) 

optimizer = tf.train.\ GradientDescentOptimizer(learning_rate).minimize(cost) 

#Plot settings 
avg_set = [] 
epoch_set = [] 

# Initializing the variables init = tf.initialize_all_variables()
# Launch the graph 
with tf.Session() as sess:
   sess.run(init)
   
   # Training cycle
   for epoch in range(training_epochs):
      avg_cost = 0.
      total_batch = int(mnist.train.num_examples/batch_size)
      
      # Loop over all batches
      for i in range(total_batch):
         batch_xs, batch_ys = \ mnist.train.next_batch(batch_size)
         # Fit training using batch data sess.run(optimizer, \ feed_dict = {
            x: batch_xs, y: batch_ys}) 
         # Compute average loss avg_cost += sess.run(cost, \ feed_dict = {
            x: batch_xs, \ y: batch_ys})/total_batch
      # Display logs per epoch step
      if epoch % display_step == 0:
         print ("Epoch:", '%04d' % (epoch+1), "cost=", "{:.9f}".format(avg_cost))
            avg_set.append(avg_cost) epoch_set.append(epoch+1)
   print ("Training phase finished")
    
   plt.plot(epoch_set,avg_set, 'o', label = 'Logistic Regression Training phase') 
   plt.ylabel('cost') 
   plt.xlabel('epoch') 
   plt.legend() 
   plt.show() 
    
   # Test model 
   correct_prediction = tf.equal(tf.argmax(activation, 1), tf.argmax(y, 1)) 
   
   # Calculate accuracy 
   accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float")) print 
      ("Model accuracy:", accuracy.eval({x: mnist.test.images, y: mnist.test.labels}))

Wynik

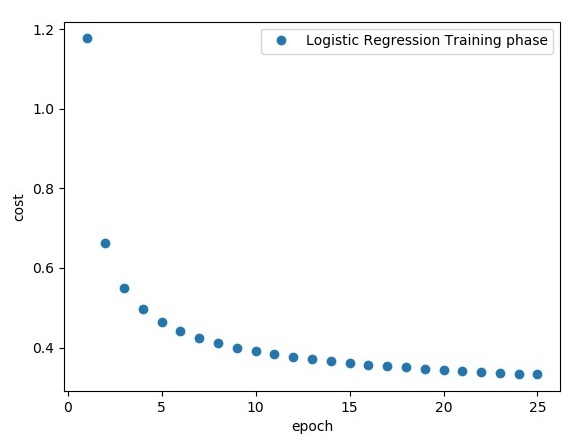
Powyższy kod generuje następujące dane wyjściowe -

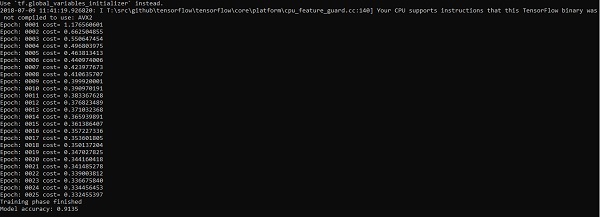
Regresja logistyczna jest uważana za analizę predykcyjną. Regresja logistyczna służy do opisu danych i wyjaśnienia związku między jedną zależną zmienną binarną a jedną lub większą liczbą zmiennych nominalnych lub niezależnych.