TensorFlow - cykliczne sieci neuronowe
Powtarzające się sieci neuronowe to rodzaj algorytmu zorientowanego na głębokie uczenie się, który opiera się na podejściu sekwencyjnym. W sieciach neuronowych zawsze zakładamy, że każde wejście i wyjście jest niezależne od wszystkich innych warstw. Tego typu sieci neuronowe są nazywane rekurencyjnymi, ponieważ wykonują obliczenia matematyczne w sposób sekwencyjny.
Rozważ następujące kroki, aby wytrenować powtarzającą się sieć neuronową -
Step 1 - Wprowadź konkretny przykład ze zbioru danych.
Step 2 - Sieć weźmie przykład i obliczy niektóre obliczenia przy użyciu losowo zainicjowanych zmiennych.
Step 3 - Następnie obliczany jest przewidywany wynik.
Step 4 - Porównanie rzeczywistego uzyskanego wyniku z wartością oczekiwaną spowoduje błąd.
Step 5 - Aby prześledzić błąd, jest on propagowany tą samą ścieżką, na której dostosowywane są również zmienne.
Step 6 - Kroki od 1 do 5 są powtarzane do momentu uzyskania pewności, że zmienne zadeklarowane w celu uzyskania wyniku są poprawnie zdefiniowane.
Step 7 - Systematyczne przewidywanie jest wykonywane przez zastosowanie tych zmiennych w celu uzyskania nowych niewidocznych danych wejściowych.
Schematyczne podejście do reprezentowania powtarzających się sieci neuronowych opisano poniżej -
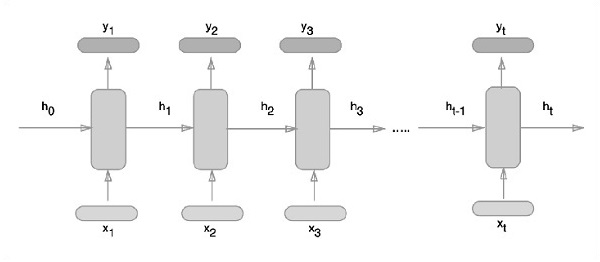
Okresowa implementacja sieci neuronowej za pomocą TensorFlow
W tej sekcji dowiemy się, jak zaimplementować rekurencyjną sieć neuronową za pomocą TensorFlow.
Step 1 - TensorFlow zawiera różne biblioteki do specyficznej implementacji modułu rekurencyjnej sieci neuronowej.
#Import necessary modules
from __future__ import print_function
import tensorflow as tf
from tensorflow.contrib import rnn
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot = True)Jak wspomniano powyżej, biblioteki pomagają w definiowaniu danych wejściowych, które stanowią podstawową część powtarzalnej implementacji sieci neuronowej.
Step 2- Naszym głównym motywem jest klasyfikacja obrazów za pomocą powtarzającej się sieci neuronowej, w której każdy wiersz obrazu traktujemy jako sekwencję pikseli. Kształt obrazu MNIST jest konkretnie zdefiniowany jako 28 * 28 pikseli. Teraz zajmiemy się 28 sekwencjami po 28 kroków dla każdej wspomnianej próbki. Zdefiniujemy parametry wejściowe, aby uzyskać sekwencyjny wzór.
n_input = 28 # MNIST data input with img shape 28*28
n_steps = 28
n_hidden = 128
n_classes = 10
# tf Graph input
x = tf.placeholder("float", [None, n_steps, n_input])
y = tf.placeholder("float", [None, n_classes]
weights = {
'out': tf.Variable(tf.random_normal([n_hidden, n_classes]))
}
biases = {
'out': tf.Variable(tf.random_normal([n_classes]))
}Step 3- Oblicz wyniki za pomocą zdefiniowanej funkcji w RNN, aby uzyskać najlepsze wyniki. Tutaj każdy kształt danych jest porównywany z bieżącym kształtem wejściowym, a wyniki są obliczane w celu utrzymania współczynnika dokładności.
def RNN(x, weights, biases):
x = tf.unstack(x, n_steps, 1)
# Define a lstm cell with tensorflow
lstm_cell = rnn.BasicLSTMCell(n_hidden, forget_bias=1.0)
# Get lstm cell output
outputs, states = rnn.static_rnn(lstm_cell, x, dtype = tf.float32)
# Linear activation, using rnn inner loop last output
return tf.matmul(outputs[-1], weights['out']) + biases['out']
pred = RNN(x, weights, biases)
# Define loss and optimizer
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits = pred, labels = y))
optimizer = tf.train.AdamOptimizer(learning_rate = learning_rate).minimize(cost)
# Evaluate model
correct_pred = tf.equal(tf.argmax(pred,1), tf.argmax(y,1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))
# Initializing the variables
init = tf.global_variables_initializer()Step 4- W tym kroku uruchomimy wykres, aby uzyskać wyniki obliczeń. Pomaga to również w obliczaniu dokładności wyników testów.
with tf.Session() as sess:
sess.run(init)
step = 1
# Keep training until reach max iterations
while step * batch_size < training_iters:
batch_x, batch_y = mnist.train.next_batch(batch_size)
batch_x = batch_x.reshape((batch_size, n_steps, n_input))
sess.run(optimizer, feed_dict={x: batch_x, y: batch_y})
if step % display_step == 0:
# Calculate batch accuracy
acc = sess.run(accuracy, feed_dict={x: batch_x, y: batch_y})
# Calculate batch loss
loss = sess.run(cost, feed_dict={x: batch_x, y: batch_y})
print("Iter " + str(step*batch_size) + ", Minibatch Loss= " + \
"{:.6f}".format(loss) + ", Training Accuracy= " + \
"{:.5f}".format(acc))
step += 1
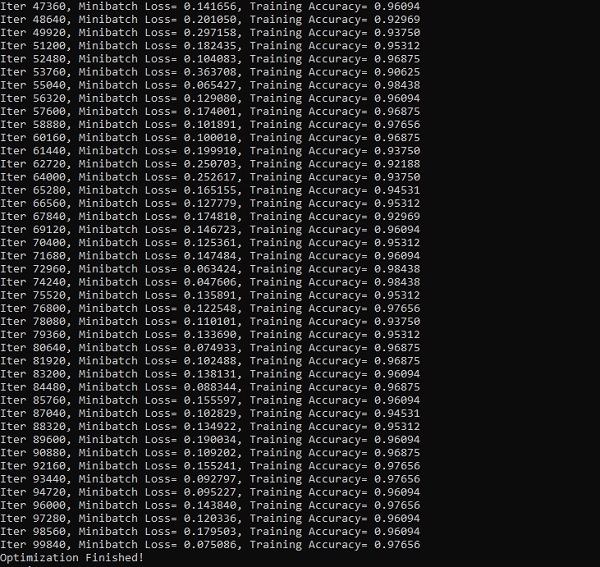
print("Optimization Finished!")
test_len = 128
test_data = mnist.test.images[:test_len].reshape((-1, n_steps, n_input))
test_label = mnist.test.labels[:test_len]
print("Testing Accuracy:", \
sess.run(accuracy, feed_dict={x: test_data, y: test_label}))Poniższe zrzuty ekranu pokazują wygenerowane dane wyjściowe -