Простые множители
Factors числа, которые мы умножаем, чтобы получить другое число.
За example, множители 14 равны 2 и 7, потому что 2 × 7 = 14.
Некоторые числа можно разложить на множители более чем одним способом.
За example, 16 можно разложить на множители как 1 × 16, 2 × 8 или 4 × 4.
Число, которое может быть разложено на множители только 1 раз, называется prime number.
Первые несколько простых чисел - 2, 3, 5, 7, 11 и 13.
Числа, состоящие из нескольких множителей, называются composite numbers.
Число 1 не является ни простым, ни составным числом.
Мы можем записать любое целое число как произведение двух факторов и начать factor tree. Факторы далее разбиваются на их факторы, пока не останутся только простые факторы, которые не могут быть далее разбиты.
Чаще всего требуется найти prime factors числа: список всех множителей простого числа данного числа.
Разложение числа на его простые множители и выражение числа как произведения его простых множителей известно как prime factorization из этого числа.
В prime factorization числа включает ТОЛЬКО простые множители, а не любые произведения этих простых множителей.
Example
Найдите простые множители 24
Решение
Step 1:
Чтобы найти простые множители 24, вы разделите его на наименьшее простое число, которое делит его поровну: 24 ÷ 2 = 12.
Step 2:
Теперь разделите 12 на наименьшее простое число, которое делится на две части: 12 ÷ 2 = 6.
Step 3:
Теперь разделите 6 на наименьшее простое число, которое делит его равномерно: 6 ÷ 2 = 3.
Step 4:
Поскольку 3 является простым числом, факторизация завершается, и факторизация числа 24 на простые множители составляет 2 × 2 × 2 × 3.
Найдите все простые делители числа 48.
Решение
Step 1:
Мы можем разбить 48 на факторы, как показано ниже.
48 = 3 × 16;
16 = 2 × 8;
8 = 2 × 4;
4 = 2 × 2.
Step 2:
Полученное здесь факторное дерево показано ниже.
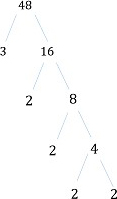
Step 3:
Итак, 48, записанное как произведение его простых множителей или разложение 48 на простые множители, равно
48 = 2 × 2 × 2 × 2 × 3
Найдите все простые делители числа 75.
Решение
Step 1:
Мы можем разбить 75 на факторы, как показано ниже.
75 = 3 × 25;
25 = 5 × 5;
Step 2:
Полученное здесь факторное дерево показано ниже.
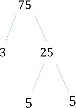
Step 3:
Итак, 75, записанное как произведение его простых множителей или факторизации на простые множители 75, равно
75 = 3 × 5 × 5