การแปลง 2D
การเปลี่ยนแปลงหมายถึงการเปลี่ยนกราฟิกบางส่วนเป็นอย่างอื่นโดยใช้กฎ เราสามารถเปลี่ยนรูปแบบได้หลายแบบเช่นการแปลการปรับขนาดขึ้นหรือลงการหมุนการตัดเฉือน ฯลฯ เมื่อการเปลี่ยนแปลงเกิดขึ้นบนระนาบ 2 มิติจะเรียกว่าการแปลง 2 มิติ
การแปลงร่างมีบทบาทสำคัญในคอมพิวเตอร์กราฟิกเพื่อจัดตำแหน่งกราฟิกบนหน้าจอและเปลี่ยนขนาดหรือการวางแนว
พิกัดที่เป็นเนื้อเดียวกัน
ในการดำเนินการตามลำดับของการเปลี่ยนแปลงเช่นการแปลตามด้วยการหมุนและการปรับขนาดเราจำเป็นต้องทำตามกระบวนการตามลำดับ -
- แปลพิกัด
- หมุนพิกัดที่แปลแล้วจากนั้น
- ปรับขนาดพิกัดที่หมุนเพื่อทำการแปลงคอมโพสิตให้เสร็จสมบูรณ์
เพื่อให้กระบวนการนี้สั้นลงเราต้องใช้เมทริกซ์การแปลง 3 × 3 แทนเมทริกซ์การแปลง 2 × 2 ในการแปลงเมทริกซ์ 2 × 2 เป็นเมทริกซ์ 3 × 3 เราต้องเพิ่มพิกัดดัมมี่พิเศษ W
ด้วยวิธีนี้เราสามารถแทนจุดด้วยตัวเลข 3 ตัวแทนที่จะเป็น 2 จำนวนซึ่งเรียกว่า Homogenous Coordinateระบบ. ในระบบนี้เราสามารถแสดงสมการการแปลงทั้งหมดในการคูณเมทริกซ์ จุดคาร์ทีเซียน P (X, Y) สามารถแปลงเป็นพิกัดที่เป็นเนื้อเดียวกันได้โดย P '(X h , Y h , h)
การแปล
การแปลจะย้ายวัตถุไปยังตำแหน่งอื่นบนหน้าจอ คุณสามารถแปลจุดใน 2 มิติได้โดยเพิ่มพิกัดการแปล (t x , t y ) ไปยังพิกัดเดิม (X, Y) เพื่อรับพิกัดใหม่ (X ', Y')
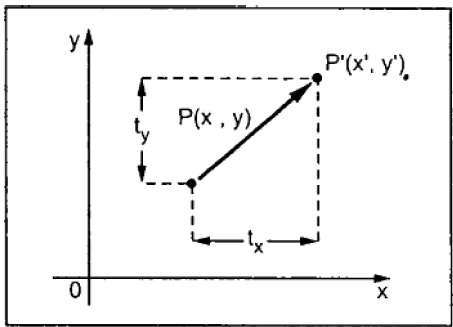
จากรูปด้านบนคุณสามารถเขียนได้ว่า -
X’ = X + tx
Y’ = Y + ty
คู่ (t x , t y ) เรียกว่าเวกเตอร์การแปลหรือกะเวกเตอร์ สมการข้างต้นสามารถแสดงโดยใช้เวกเตอร์คอลัมน์
$ P = \ frac {[X]} {[Y]} $ p '= $ \ frac {[X']} {[Y ']} $ T = $ \ frac {[t_ {x}]} {[ t_ {y}]} $
เราสามารถเขียนเป็น -
P’ = P + T
การหมุน
ในการหมุนเราหมุนวัตถุที่มุมเฉพาะθ (theta) จากจุดกำเนิด จากรูปต่อไปนี้เราจะเห็นว่าจุด P (X, Y) อยู่ที่มุมφจากพิกัด X แนวนอนโดยมีระยะทาง r จากจุดกำเนิด
สมมติว่าคุณต้องการหมุนที่มุมθ หลังจากหมุนไปยังตำแหน่งใหม่คุณจะได้รับจุดใหม่ P '(X', Y ')

การใช้ตรีโกณมิติมาตรฐานพิกัดดั้งเดิมของจุด P (X, Y) สามารถแสดงเป็น -
$ X = r \, cos \, \ phi ...... (1) $
$ Y = r \, sin \, \ phi ...... (2) $
เช่นเดียวกับที่เราสามารถแทนจุด P '(X', Y ') เป็น -
$ {x} '= r \: cos \: \ left (\ phi \: + \: \ theta \ right) = r \: cos \: \ phi \: cos \: \ theta \: - \: r \ : sin \: \ phi \: sin \: \ theta ....... (3) $
$ {y} '= r \: sin \: \ left (\ phi \: + \: \ theta \ right) = r \: cos \: \ phi \: sin \: \ theta \: + \: r \ : บาป \: \ phi \: cos \: \ theta ....... (4) $
การแทนสมการ (1) & (2) ใน (3) & (4) ตามลำดับเราจะได้
$ {x} '= x \: cos \: \ theta - \: y \: sin \: \ theta $
$ {y} '= x \: sin \: \ theta + \: y \: cos \: \ theta $
แทนสมการข้างต้นในรูปแบบเมทริกซ์
$$ [X 'Y'] = [XY] \ begin {bmatrix} cos \ theta & sin \ theta \\ −sin \ theta & cos \ theta \ end {bmatrix} หรือ $$
P '= ป. ร
โดยที่ R คือเมทริกซ์การหมุน
$$ R = \ begin {bmatrix} cos \ theta & sin \ theta \\ −sin \ theta & cos \ theta \ end {bmatrix} $$
มุมการหมุนสามารถเป็นบวกและลบได้
สำหรับมุมการหมุนที่เป็นบวกเราสามารถใช้เมทริกซ์การหมุนด้านบนได้ อย่างไรก็ตามสำหรับการหมุนมุมลบเมทริกซ์จะเปลี่ยนไปตามที่แสดงด้านล่าง -
$$ R = \ begin {bmatrix} cos (- \ theta) & sin (- \ theta) \\ -sin (- \ theta) & cos (- \ theta) \ end {bmatrix} $$
$$ = \ start {bmatrix} cos \ theta & −sin \ theta \\ sin \ theta & cos \ theta \ end {bmatrix} \ left (\ เพราะ cos (- \ theta) = cos \ theta \; และ \; บาป (- \ theta) = −sin \ theta \ right) $$
การปรับขนาด
ในการเปลี่ยนขนาดของวัตถุจะใช้การแปลงมาตราส่วน ในขั้นตอนการปรับขนาดคุณจะขยายหรือบีบอัดขนาดของวัตถุ การปรับมาตราส่วนสามารถทำได้โดยการคูณพิกัดเดิมของวัตถุด้วยตัวคูณมาตราส่วนเพื่อให้ได้ผลลัพธ์ที่ต้องการ
ให้เราสมมติว่าพิกัดเดิมคือ (X, Y) ปัจจัยการปรับขนาดคือ (S X , S Y ) และพิกัดที่ผลิตคือ (X ', Y') สิ่งนี้สามารถแสดงทางคณิตศาสตร์ได้ดังที่แสดงด้านล่าง -
X' = X . SX and Y' = Y . SY
ปัจจัยการปรับขนาด S X , S Y จะปรับขนาดวัตถุในทิศทาง X และ Y ตามลำดับ สมการข้างต้นสามารถแสดงในรูปแบบเมทริกซ์ดังต่อไปนี้ -
$$ \ binom {X '} {Y'} = \ binom {X} {Y} \ begin {bmatrix} S_ {x} & 0 \\ 0 & S_ {y} \ end {bmatrix} $$
หรือ
P’ = P . S
โดยที่ S คือเมทริกซ์มาตราส่วน ขั้นตอนการปรับขนาดจะแสดงในรูปต่อไปนี้
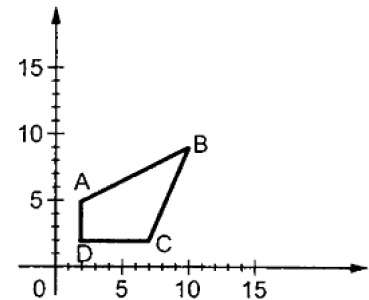
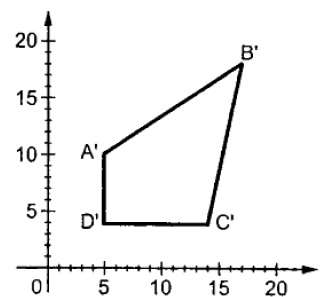
ถ้าเราให้ค่าน้อยกว่า 1 ให้กับค่ามาตราส่วน S เราก็สามารถลดขนาดของวัตถุได้ หากเราให้ค่ามากกว่า 1 เราก็สามารถเพิ่มขนาดของวัตถุได้
การสะท้อนกลับ
การสะท้อนเป็นภาพสะท้อนของวัตถุดั้งเดิม กล่าวอีกนัยหนึ่งเราสามารถพูดได้ว่าเป็นการหมุน 180 ° ในการเปลี่ยนแปลงการสะท้อนขนาดของวัตถุจะไม่เปลี่ยนแปลง
ตัวเลขต่อไปนี้แสดงการสะท้อนตามแกน X และ Y และเกี่ยวกับจุดกำเนิดตามลำดับ
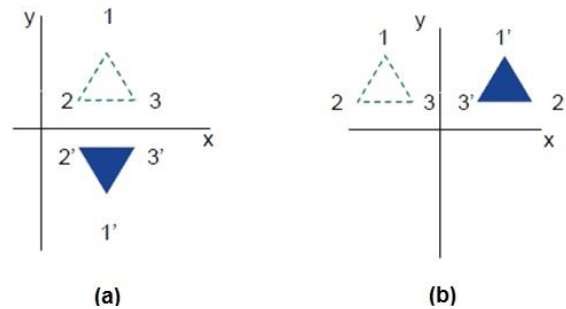
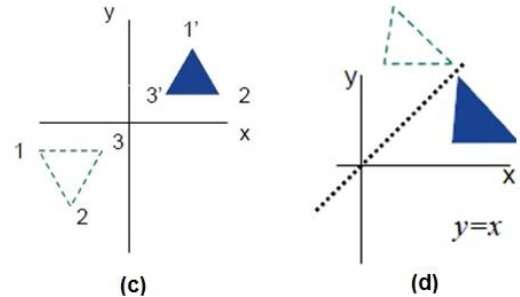
เฉือน
การเปลี่ยนแปลงที่เอียงรูปร่างของวัตถุเรียกว่าการแปลงเฉือน มีการแปลงเฉือนสองแบบX-Shear และ Y-Shear. หนึ่งกะค่าพิกัด X และค่าพิกัด Y กะอื่น ๆ อย่างไรก็ตาม; ในทั้งสองกรณีมีเพียงพิกัดเดียวเท่านั้นที่เปลี่ยนพิกัดและอื่น ๆ จะรักษาค่าไว้ การตัดเฉือนเรียกอีกอย่างว่าSkewing.
X-Shear
X-Shear จะรักษาพิกัด Y และทำการเปลี่ยนแปลงกับพิกัด X ซึ่งทำให้เส้นแนวตั้งเอียงไปทางขวาหรือซ้ายดังแสดงในรูปด้านล่าง
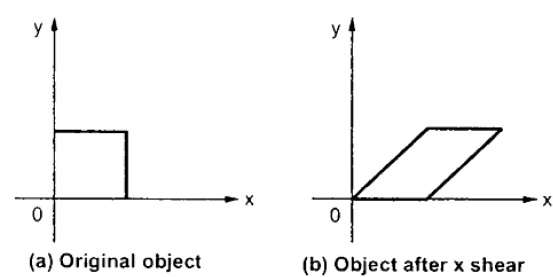
เมทริกซ์การเปลี่ยนแปลงสำหรับ X-Shear สามารถแสดงเป็น -
$$ X_ {sh} = \ begin {bmatrix} 1 & shx & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} $$
Y '= Y + Sh y . X
X '= X
Y- เฉือน
Y-Shear รักษาพิกัด X และเปลี่ยนพิกัด Y ซึ่งทำให้เส้นแนวนอนเปลี่ยนเป็นเส้นที่ลาดขึ้นหรือลงดังแสดงในรูปต่อไปนี้
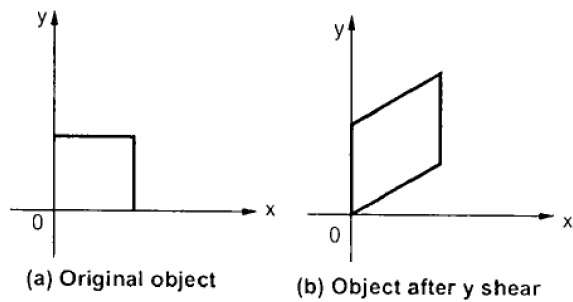
Y-Shear สามารถแสดงในเมทริกซ์จาก -
$$ Y_ {sh} \ begin {bmatrix} 1 & 0 & 0 \\ shy & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} $$
X'= X + Sh x ย
Y '= Y
การแปลงคอมโพสิต
หากการแปลงระนาบ T1 ตามด้วยการแปลงระนาบที่สอง T2 ผลลัพธ์นั้นอาจถูกแทนด้วยการแปลงเดี่ยว T ซึ่งเป็นองค์ประกอบของ T1 และ T2 ตามลำดับนั้น สิ่งนี้เขียนเป็น T = T1 ∙ T2
การแปลงคอมโพสิตสามารถทำได้โดยการต่อเมทริกซ์การแปลงเพื่อให้ได้เมทริกซ์การแปลงแบบรวม
เมทริกซ์รวม -
[T][X] = [X] [T1] [T2] [T3] [T4] …. [Tn]
โดยที่ [Ti] คือการรวมกันของ
- Translation
- Scaling
- Shearing
- Rotation
- Reflection
การเปลี่ยนแปลงลำดับของการแปลงจะนำไปสู่ผลลัพธ์ที่แตกต่างกันเนื่องจากโดยทั่วไปการคูณเมทริกซ์จะไม่สะสมนั่นคือ [A] [B] ≠ [B]. [A] และลำดับการคูณ จุดประสงค์พื้นฐานของการสร้างการเปลี่ยนแปลงคือการเพิ่มประสิทธิภาพโดยใช้การแปลงแบบประกอบเพียงครั้งเดียวไปยังจุดหนึ่งแทนที่จะใช้ชุดของการเปลี่ยนแปลงทีละอย่าง
ตัวอย่างเช่นในการหมุนวัตถุเกี่ยวกับจุดใดจุดหนึ่ง (X p , Y p ) เราต้องดำเนินการสามขั้นตอน -
- แปลจุด (X p , Y p ) เป็นจุดเริ่มต้น
- หมุนมันเกี่ยวกับจุดกำเนิด
- สุดท้ายให้แปลจุดศูนย์กลางของการหมุนกลับที่เดิม