อัลกอริทึมการเติมรูปหลายเหลี่ยม
รูปหลายเหลี่ยมเป็นรายการเรียงลำดับของจุดยอดดังแสดงในรูปต่อไปนี้ สำหรับการเติมรูปหลายเหลี่ยมด้วยสีเฉพาะคุณต้องกำหนดพิกเซลที่ตกลงบนขอบของรูปหลายเหลี่ยมและพิกเซลที่อยู่ภายในรูปหลายเหลี่ยม ในบทนี้เราจะมาดูวิธีเติมรูปหลายเหลี่ยมโดยใช้เทคนิคต่างๆ

Scan Line Algorithm
อัลกอริทึมนี้ทำงานโดยการตัดกันเส้นสแกนกับขอบรูปหลายเหลี่ยมและเติมรูปหลายเหลี่ยมระหว่างจุดตัดคู่ ขั้นตอนต่อไปนี้แสดงให้เห็นว่าอัลกอริทึมนี้ทำงานอย่างไร
Step 1 - ค้นหา Ymin และ Ymax จากรูปหลายเหลี่ยมที่กำหนด
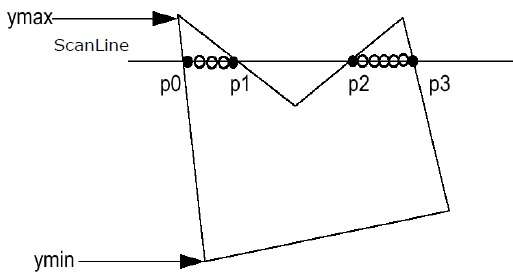
Step 2- ScanLine ตัดกับขอบแต่ละด้านของรูปหลายเหลี่ยมจาก Ymin ถึง Ymax ตั้งชื่อจุดตัดกันของรูปหลายเหลี่ยมแต่ละจุด ตามรูปที่แสดงด้านบนพวกเขาถูกตั้งชื่อเป็น p0, p1, p2, p3
Step 3 - เรียงลำดับจุดตัดตามลำดับที่เพิ่มขึ้นของพิกัด X ได้แก่ (p0, p1), (p1, p2) และ (p2, p3)
Step 4 - กรอกคู่พิกัดทั้งหมดที่อยู่ภายในรูปหลายเหลี่ยมและละเว้นคู่อื่น
อัลกอริทึมการเติมน้ำท่วม
บางครั้งเราเจอวัตถุที่ต้องการเติมเต็มพื้นที่และขอบเขตของมันด้วยสีที่ต่างกัน เราสามารถทาสีวัตถุดังกล่าวด้วยสีภายในที่ระบุแทนการค้นหาสีขอบเขตเฉพาะเช่นเดียวกับอัลกอริทึมการเติมขอบเขต
แทนที่จะอาศัยขอบเขตของวัตถุ แต่อาศัยสีเติม กล่าวอีกนัยหนึ่งคือแทนที่สีภายในของวัตถุด้วยสีเติม เมื่อไม่มีพิกเซลของสีภายในดั้งเดิมอีกต่อไปอัลกอริทึมจะเสร็จสมบูรณ์
อีกครั้งอัลกอริทึมนี้อาศัยวิธีการเชื่อมต่อแบบ Four-connect หรือ Eight-connect ในการเติมพิกเซล แต่แทนที่จะมองหาสีขอบเขตมันกำลังมองหาพิกเซลที่อยู่ติดกันทั้งหมดที่เป็นส่วนหนึ่งของการตกแต่งภายใน
อัลกอริทึมการเติมขอบเขต
อัลกอริทึมการเติมขอบเขตทำงานเป็นชื่อของมัน อัลกอริทึมนี้เลือกจุดภายในวัตถุและเริ่มเติมจนกว่าจะถึงขอบเขตของวัตถุ สีของขอบเขตและสีที่เราเติมควรแตกต่างกันเพื่อให้อัลกอริทึมนี้ทำงานได้
ในอัลกอริทึมนี้เราถือว่าสีของขอบเขตนั้นเหมือนกันสำหรับวัตถุทั้งหมด อัลกอริทึมการเติมขอบเขตสามารถใช้งานได้โดยพิกเซลที่เชื่อมต่อ 4 พิกเซลหรือพิกเซลที่เชื่อมต่อ 8 พิกเซล
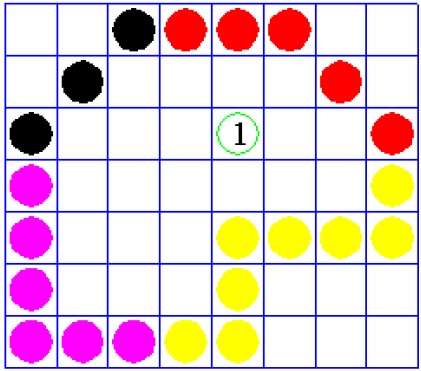
รูปหลายเหลี่ยมที่เชื่อมต่อ 4 รูปแบบ
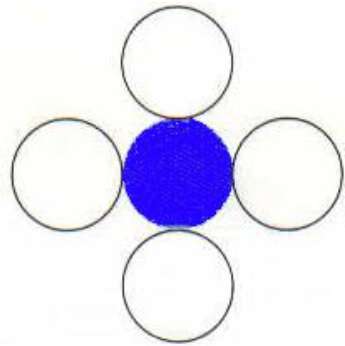
ในเทคนิคนี้ใช้พิกเซลที่เชื่อมต่อ 4 จุดดังแสดงในรูป เรากำลังวางพิกเซลด้านบนด้านล่างไปทางขวาและทางด้านซ้ายของพิกเซลปัจจุบันและกระบวนการนี้จะดำเนินต่อไปจนกว่าเราจะพบขอบเขตที่มีสีต่างกัน
อัลกอริทึม
Step 1 - เริ่มต้นค่าของ seed point (seedx, seedy), fcolor และ dcol
Step 2 - กำหนดค่าขอบเขตของรูปหลายเหลี่ยม
Step 3 - ตรวจสอบว่าจุดเริ่มต้นปัจจุบันเป็นสีเริ่มต้นหรือไม่จากนั้นทำซ้ำขั้นตอนที่ 4 และ 5 จนกระทั่งถึงพิกเซลขอบเขต
If getpixel(x, y) = dcol then repeat step 4 and 5Step 4 - เปลี่ยนสีเริ่มต้นด้วยสีเติมที่จุดเริ่มต้น
setPixel(seedx, seedy, fcol)Step 5 - ทำตามขั้นตอนซ้ำ ๆ โดยมีจุดใกล้เคียงสี่จุด
FloodFill (seedx – 1, seedy, fcol, dcol)
FloodFill (seedx + 1, seedy, fcol, dcol)
FloodFill (seedx, seedy - 1, fcol, dcol)
FloodFill (seedx – 1, seedy + 1, fcol, dcol)Step 6 - ออก
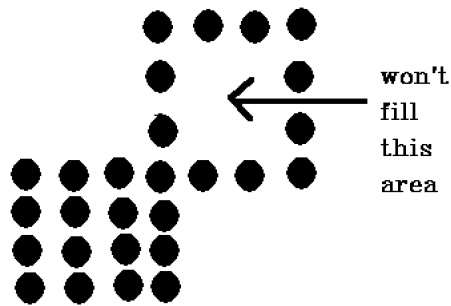
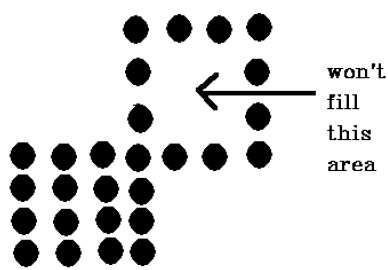
มีปัญหากับเทคนิคนี้ พิจารณากรณีดังที่แสดงด้านล่างที่เราพยายามเติมเต็มทั้งภูมิภาค ที่นี่ภาพจะเต็มไปเพียงบางส่วน ในกรณีเช่นนี้ไม่สามารถใช้เทคนิค 4-connected pixels ได้
รูปหลายเหลี่ยมที่เชื่อมต่อกัน 8 รูป
ในเทคนิคนี้จะใช้พิกเซลที่เชื่อมต่อ 8 พิกเซลดังแสดงในรูป เราวางพิกเซลไว้ด้านบนด้านล่างด้านขวาและด้านซ้ายของพิกเซลปัจจุบันตามที่เราทำในเทคนิค 4-connected
นอกจากนี้เรายังวางพิกเซลในแนวทแยงมุมเพื่อให้ครอบคลุมพื้นที่ทั้งหมดของพิกเซลปัจจุบัน กระบวนการนี้จะดำเนินต่อไปจนกว่าเราจะพบขอบเขตที่มีสีต่างกัน

อัลกอริทึม
Step 1 - เริ่มต้นค่าของ seed point (seedx, seedy), fcolor และ dcol
Step 2 - กำหนดค่าขอบเขตของรูปหลายเหลี่ยม
Step 3 - ตรวจสอบว่าจุดเริ่มต้นปัจจุบันเป็นสีเริ่มต้นหรือไม่จากนั้นทำซ้ำขั้นตอนที่ 4 และ 5 จนกระทั่งถึงพิกเซลขอบเขต
If getpixel(x,y) = dcol then repeat step 4 and 5Step 4 - เปลี่ยนสีเริ่มต้นด้วยสีเติมที่จุดเริ่มต้น
setPixel(seedx, seedy, fcol)Step 5 - ทำตามขั้นตอนซ้ำ ๆ โดยมีจุดใกล้เคียงสี่จุด
FloodFill (seedx – 1, seedy, fcol, dcol)
FloodFill (seedx + 1, seedy, fcol, dcol)
FloodFill (seedx, seedy - 1, fcol, dcol)
FloodFill (seedx, seedy + 1, fcol, dcol)
FloodFill (seedx – 1, seedy + 1, fcol, dcol)
FloodFill (seedx + 1, seedy + 1, fcol, dcol)
FloodFill (seedx + 1, seedy - 1, fcol, dcol)
FloodFill (seedx – 1, seedy - 1, fcol, dcol)Step 6 - ออก
เทคนิคพิกเซลที่เชื่อมต่อ 4 จุดล้มเหลวในการเติมเต็มพื้นที่ตามที่ทำเครื่องหมายในรูปต่อไปนี้ซึ่งจะไม่เกิดขึ้นกับเทคนิค 8-connected
การทดสอบภายใน - ภายนอก
วิธีนี้เรียกอีกอย่างว่า counting number method. ในขณะเติมวัตถุเรามักจะต้องระบุว่าจุดใดจุดหนึ่งอยู่ภายในวัตถุหรือภายนอกวัตถุนั้น มีสองวิธีที่เราสามารถระบุได้ว่าจุดใดจุดหนึ่งอยู่ภายในวัตถุหรือภายนอก
- กฎคี่ - คู่
- กฎเลขที่คดเคี้ยวไม่ใช่ศูนย์
กฎคี่ - คู่
ในเทคนิคนี้เราจะนับขอบที่ข้ามไปตามเส้นจากจุดใด ๆ (x, y) ถึงอินฟินิตี้ ถ้าจำนวนการโต้ตอบเป็นเลขคี่จุด (x, y) คือจุดภายใน และถ้าจำนวนการโต้ตอบเป็นจำนวนเท่ากันจุด (x, y) ก็คือจุดภายนอก ตัวอย่างต่อไปนี้แสดงให้เห็นถึงแนวคิดนี้
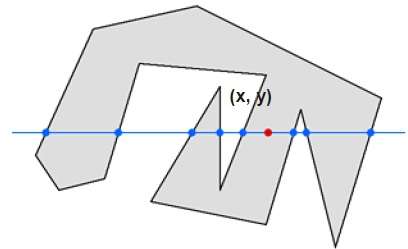
จากรูปด้านบนเราจะเห็นว่าจากจุด (x, y) จำนวนจุดปฏิสัมพันธ์ทางด้านซ้ายคือ 5 และทางด้านขวาคือ 3 จากปลายทั้งสองข้างจำนวนจุดปฏิสัมพันธ์จะเป็นเลขคี่ จุดจะพิจารณาภายในวัตถุ
กฎเลขที่คดเคี้ยวที่ไม่ใช่ศูนย์
วิธีนี้ยังใช้กับรูปหลายเหลี่ยมธรรมดาเพื่อทดสอบจุดที่กำหนดว่าอยู่ภายในหรือไม่ สามารถเข้าใจได้ง่ายๆด้วยความช่วยเหลือของหมุดและแถบยาง ยึดหมุดที่ขอบด้านใดด้านหนึ่งของรูปหลายเหลี่ยมแล้วมัดแถบยางเข้าด้วยกันจากนั้นยืดแถบยางตามขอบของรูปหลายเหลี่ยม
เมื่อขอบทั้งหมดของรูปหลายเหลี่ยมถูกรัดด้วยแถบยางให้ตรวจสอบหมุดที่ยึดไว้ตรงจุดที่จะทดสอบ ถ้าเราพบลมอย่างน้อยหนึ่งจุดให้พิจารณาภายในรูปหลายเหลี่ยมมิฉะนั้นเราสามารถพูดได้ว่าจุดนั้นไม่ได้อยู่ในรูปหลายเหลี่ยม
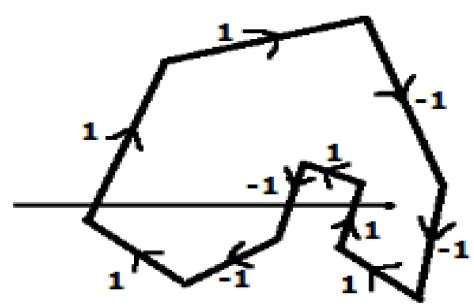
ในวิธีอื่นให้บอกทิศทางไปยังขอบทั้งหมดของรูปหลายเหลี่ยม ลากเส้นสแกนจากจุดที่จะทดสอบไปทางซ้ายสุดของทิศทาง X
ให้ค่า 1 กับขอบทั้งหมดซึ่งจะขึ้นไปและ -1 อื่น ๆ ทั้งหมดเป็นค่าทิศทาง
ตรวจสอบค่าทิศทางขอบที่เส้นสแกนกำลังผ่านและสรุปผล
หากผลรวมทั้งหมดของค่าทิศทางนี้ไม่เป็นศูนย์จุดที่จะทดสอบนี้คือ interior point, มิฉะนั้นจะเป็นไฟล์ exterior point.
ในรูปด้านบนเราสรุปค่าทิศทางที่เส้นสแกนกำลังผ่านจากนั้นผลรวมคือ 1 - 1 + 1 = 1; ซึ่งไม่ใช่ศูนย์ ดังนั้นจุดที่กล่าวว่าเป็นจุดภายใน