การแปลง 3D

การหมุน

การหมุน 3 มิติไม่เหมือนกับการหมุน 2 มิติ ในการหมุน 3 มิติเราต้องระบุมุมของการหมุนพร้อมกับแกนของการหมุน เราสามารถทำการหมุน 3 มิติเกี่ยวกับแกน X, Y และ Z แสดงในรูปแบบเมทริกซ์ดังต่อไปนี้ -

$$ R_ {x} (\ theta) = \ begin {bmatrix} 1 & 0 & 0 & 0 & 0 \\ 0 & cos \ theta & −sin \ theta & 0 \\ 0 & sin \ theta & cos \ theta & 0 \\ 0 & 0 & 0 & 1 \ \ \ end {bmatrix} R_ {y} (\ theta) = \ begin {bmatrix} cos \ theta & 0 & sin \ theta & 0 \\ 0 & 1 & 0 & 0 \\ −sin \ theta & 0 & cos \ theta & 0 \\ 0 & 0 & 0 & 1 \\ \ end {bmatrix} R_ {z} (\ theta) = \ begin {bmatrix} cos \ theta & −sin \ theta & 0 & 0 \\ sin \ theta & cos \ theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \ end {bmatrix} $$

รูปต่อไปนี้อธิบายการหมุนเกี่ยวกับแกนต่างๆ -

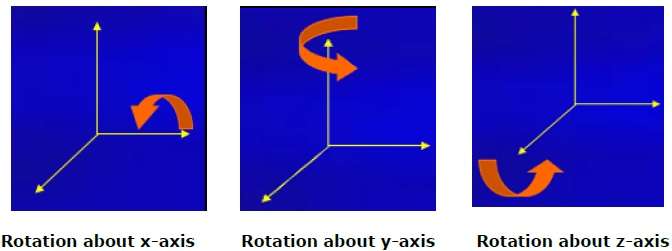
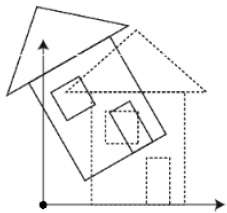
การปรับขนาด

คุณสามารถเปลี่ยนขนาดของวัตถุโดยใช้การแปลงมาตราส่วน ในกระบวนการปรับขนาดคุณอาจขยายหรือบีบอัดขนาดของวัตถุ การปรับมาตราส่วนสามารถทำได้โดยการคูณพิกัดเดิมของวัตถุด้วยตัวคูณมาตราส่วนเพื่อให้ได้ผลลัพธ์ที่ต้องการ รูปต่อไปนี้แสดงผลของการปรับขนาด 3D -

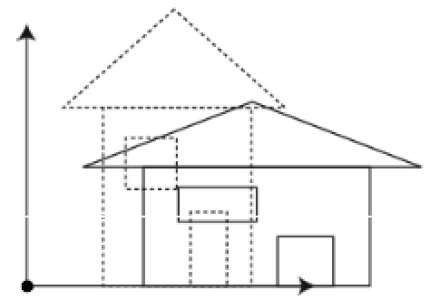
ในการดำเนินการปรับมาตราส่วน 3 มิติจะใช้พิกัดสามพิกัด ให้เราสมมติว่าพิกัดเดิมคือ (X, Y, Z) ปัจจัยการปรับขนาดคือ $ (S_ {X,} S_ {Y,} S_ {z}) $ ตามลำดับและพิกัดที่ผลิตคือ (X ', Y' , Z '). สิ่งนี้สามารถแสดงทางคณิตศาสตร์ได้ดังที่แสดงด้านล่าง -

$ S = \ begin {bmatrix} S_ {x} & 0 & 0 & 0 \\ 0 & S_ {y} & 0 & 0 \\ 0 & 0 & S_ {z} & 0 \\ 0 & 0 & 0 & 1 \ end {bmatrix} $

P '= P ∙ S

$ [{X} '\: \: \: {Y}' \: \: \: {Z} '\: \: \: 1] = [X \: \: \: Y \: \: \: Z \: \: \: 1] \: \: \ begin {bmatrix} S_ {x} & 0 & 0 & 0 \\ 0 & S_ {y} & 0 & 0 \\ 0 & 0 & S_ {z} & 0 \\ 0 & 0 & 0 & 1 \ end {bmatrix} $

$ = [X.S_ {x} \: \: \: Y.S_ {y} \: \: \: Z.S_ {z} \: \: \: 1] $

เฉือน

การเปลี่ยนแปลงที่เอียงรูปร่างของวัตถุเรียกว่า shear transformation. เช่นเดียวกับการเฉือนแบบ 2 มิติเราสามารถเฉือนวัตถุตามแกน X แกน Y หรือแกน Z ในแบบ 3 มิติได้

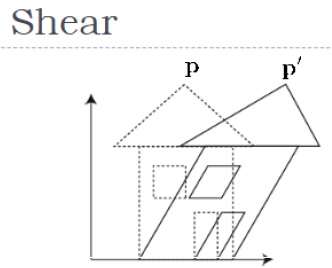
ดังที่แสดงในรูปด้านบนมีพิกัด P คุณสามารถเฉือนมันเพื่อให้ได้พิกัด P 'ใหม่ซึ่งสามารถแสดงในรูปแบบเมทริกซ์ 3 มิติดังต่อไปนี้ -

$ Sh = \ begin {bmatrix} 1 & sh_ {x} ^ {y} & sh_ {x} ^ {z} & 0 \\ sh_ {y} ^ {x} & 1 & sh_ {y} ^ {z} & 0 \\ sh_ {z} ^ {x} & sh_ {z} ^ {y} & 1 & 0 \\ 0 & 0 & 0 & 1 \ end {bmatrix} $

P '= P ∙ช

$ X '= X + Sh_ {x} ^ {y} Y + Sh_ {x} ^ {z} Z $

$ Y '= Sh_ {y} ^ {x} X + Y + sh_ {y} ^ {z} Z $

$ Z '= Sh_ {z} ^ {x} X + Sh_ {z} ^ {y} Y + Z $

เมทริกซ์การเปลี่ยนแปลง

เมทริกซ์การแปลงร่างเป็นเครื่องมือพื้นฐานสำหรับการเปลี่ยนแปลง เมทริกซ์ที่มีขนาด nxm ถูกคูณด้วยพิกัดของวัตถุ โดยปกติเมทริกซ์ 3 x 3 หรือ 4 x 4 จะใช้สำหรับการแปลง ตัวอย่างเช่นพิจารณาเมทริกซ์ต่อไปนี้สำหรับการดำเนินการต่างๆ

$ T = \ begin {bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ t_ {x} & t_ {y} & t_ {z} & 1 \\ \ end {bmatrix} $	$ S = \ begin {bmatrix} S_ {x} & 0 & 0 & 0 \\ 0 & S_ {y} & 0 & 0 \\ 0 & 0 & S_ {z} & 0 \\ 0 & 0 & 0 & 1 \ end {bmatrix} $	$ Sh = \ begin {bmatrix} 1 & sh_ {x} ^ {y} & sh_ {x} ^ {z} & 0 \\ sh_ {y} ^ {x} & 1 & sh_ {y} ^ {z} & 0 \\ sh_ {z} ^ {x} & sh_ {z} ^ {y} & 1 & 0 \\ 0 & 0 & 0 & 1 \ end {bmatrix} $
Translation Matrix	Scaling Matrix	Shear Matrix
$ R_ {x} (\ theta) = \ begin {bmatrix} 1 & 0 & 0 & 0 & 0 \\ 0 & cos \ theta & -sin \ theta & 0 \\ 0 & sin \ theta & cos \ theta & 0 \\ 0 & 0 & 0 & 1 \\ \ end {bmatrix} $	$ R_ {y} (\ theta) = \ begin {bmatrix} cos \ theta & 0 & sin \ theta & 0 \\ 0 & 1 & 0 & 0 \\ -sin \ theta & 0 & cos \ theta & 0 \\ 0 & 0 & 0 & 1 \\ \ end {bmatrix} $	$ R_ {z} (\ theta) = \ begin {bmatrix} cos \ theta & -sin \ theta & 0 & 0 \\ sin \ theta & cos \ theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \ end {bmatrix} $
Rotation Matrix