พื้นผิวคอมพิวเตอร์กราฟิก

พื้นผิวรูปหลายเหลี่ยม

วัตถุถูกแสดงเป็นชุดของพื้นผิว การแสดงวัตถุ 3 มิติแบ่งออกเป็นสองประเภท

• Boundary Representations (B-reps) - อธิบายวัตถุ 3 มิติว่าเป็นชุดของพื้นผิวที่แยกการตกแต่งภายในของวัตถุออกจากสภาพแวดล้อม

• Space–partitioning representations - ใช้เพื่ออธิบายคุณสมบัติภายในโดยแบ่งพื้นที่เชิงพื้นที่ที่มีวัตถุเป็นชุดของของแข็งขนาดเล็กที่ไม่ทับซ้อนกัน (โดยปกติจะเป็นก้อน)

การแสดงขอบเขตที่ใช้บ่อยที่สุดสำหรับวัตถุกราฟิก 3 มิติคือชุดของรูปหลายเหลี่ยมพื้นผิวที่ล้อมรอบภายในวัตถุ ระบบกราฟิกจำนวนมากใช้วิธีนี้ ชุดรูปหลายเหลี่ยมถูกเก็บไว้สำหรับคำอธิบายวัตถุ สิ่งนี้ช่วยลดความซับซ้อนและเร่งความเร็วในการแสดงพื้นผิวและการแสดงวัตถุเนื่องจากพื้นผิวทั้งหมดสามารถอธิบายได้ด้วยสมการเชิงเส้น

พื้นผิวรูปหลายเหลี่ยมเป็นเรื่องปกติในการออกแบบและการสร้างแบบจำลองที่มั่นคงเนื่องจาก wireframe displayสามารถทำได้อย่างรวดเร็วเพื่อแสดงโครงสร้างพื้นผิวโดยทั่วไป จากนั้นฉากที่สมจริงจะถูกสร้างขึ้นโดยการสอดแทรกรูปแบบการแรเงาบนพื้นผิวรูปหลายเหลี่ยมเพื่อให้แสงสว่าง

ตารางรูปหลายเหลี่ยม

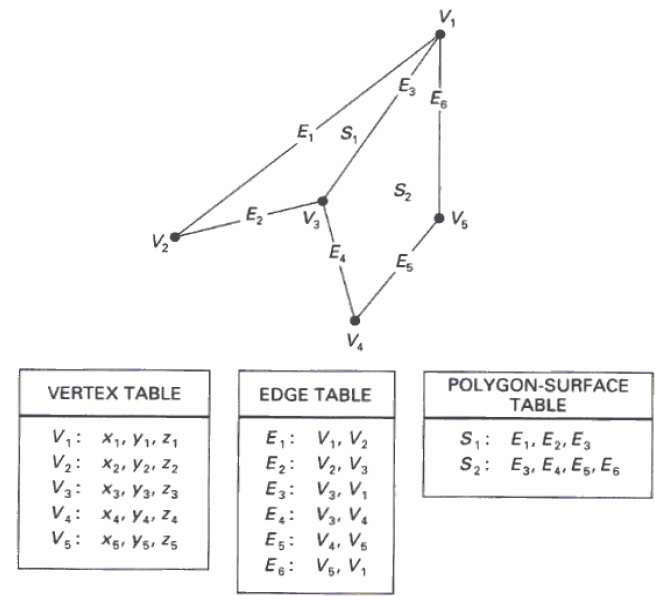
ในวิธีนี้พื้นผิวถูกระบุโดยชุดพิกัดจุดยอดและแอตทริบิวต์ที่เกี่ยวข้อง ดังแสดงในรูปต่อไปนี้มีห้าจุดจาก v ₁ไปทาง v 5

• ร้านค้ายอดแต่ละ x, y, z และข้อมูลพิกัดซึ่งเป็นตัวแทนในตารางเป็นโวลต์₁ : x ₁ , y ₁ , Z 1

• ตาราง Edge ใช้เพื่อเก็บข้อมูลขอบของรูปหลายเหลี่ยม ในรูปต่อไปขอบ E ₁อยู่ระหว่างจุดสุดยอดวี₁และวี₂ซึ่งเป็นตัวแทนในตารางเป็น E ₁ : โวลต์₁โวลต์2

• ตารางพื้นผิวรูปหลายเหลี่ยมเก็บจำนวนพื้นผิวที่มีอยู่ในรูปหลายเหลี่ยม จากตัวเลขดังต่อไปนี้พื้นผิว S ₁ถูกปกคลุมด้วยขอบ E ₁ , E ₂และอี₃ซึ่งสามารถแสดงในตารางพื้นผิวรูปหลายเหลี่ยมเป็น S ₁ : E ₁ , E ₂และ E 3

สมการเครื่องบิน

สมการของพื้นผิวระนาบสามารถแสดงเป็น -

ขวาน + By + Cz + D = 0

โดยที่ (x, y, z) คือจุดใด ๆ บนระนาบและสัมประสิทธิ์ A, B, C และ D คือค่าคงที่ที่อธิบายคุณสมบัติเชิงพื้นที่ของเครื่องบิน เราสามารถรับค่าของ A, B, C และ D ได้โดยการแก้สมการระนาบสามชุดโดยใช้ค่าพิกัดสำหรับจุดที่ไม่ใช่คอลลิเนียร์สามจุดในระนาบ สมมติว่าจุดยอดสามจุดของระนาบคือ (x ₁ , y ₁ , z ₁ ), (x ₂ , y ₂ , z ₂ ) และ (x ₃ , y ₃ , z ₃ )

ให้เราแก้สมการพร้อมกันต่อไปนี้สำหรับอัตราส่วน A / D, B / D และ C / D คุณจะได้รับค่า A, B, C และ D

(A / D) x ₁ + (B / D) y ₁ + (C / D) z ₁ = -1

(A / D) x ₂ + (B / D) y ₂ + (C / D) z ₂ = -1

(A / D) x ₃ + (B / D) y ₃ + (C / D) z ₃ = -1

เพื่อให้ได้สมการข้างต้นในรูปแบบดีเทอร์มิแนนต์ให้ใช้กฎของแครมเมอร์กับสมการข้างต้น

$ A = \ begin {bmatrix} 1 & y_ {1} & z_ {1} \\ 1 & y_ {2} & z_ {2} \\ 1 & y_ {3} & z_ {3} \ end {bmatrix} B = \ เริ่มต้น {bmatrix} x_ {1} & 1 & z_ {1} \\ x_ {2} & 1 & z_ {2} \\ x_ {3} & 1 & z_ {3} \ end {bmatrix} C = \ begin {bmatrix} x_ {1} & y_ {1} & 1 \\ x_ {2} & y_ {2} & 1 \\ x_ {3} & y_ {3} & 1 \ end {bmatrix} D = - \ begin {bmatrix} x_ {1} & y_ {1} & z_ {1} \\ x_ {2} & y_ {2} & z_ {2} \\ x_ {3} & y_ {3} & z_ {3} \ end {bmatrix } $

สำหรับจุดใด ๆ (x, y, z) ที่มีพารามิเตอร์ A, B, C และ D เราสามารถพูดได้ว่า -

• Ax + By + Cz + D ≠ 0 หมายถึงจุดไม่ได้อยู่บนระนาบ

• Ax + By + Cz + D <0 หมายถึงจุดอยู่ภายในพื้นผิว

• Ax + By + Cz + D> 0 หมายถึงจุดอยู่นอกพื้นผิว

ตาข่ายรูปหลายเหลี่ยม

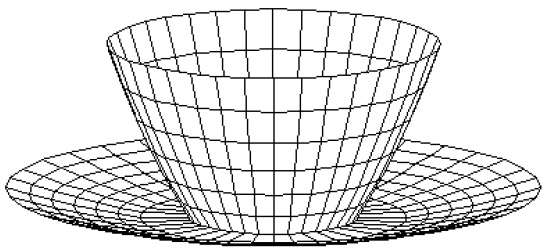
พื้นผิว 3 มิติและของแข็งสามารถประมาณได้โดยชุดขององค์ประกอบหลายเหลี่ยมและเส้น พื้นผิวดังกล่าวเรียกว่าpolygonal meshes. ในตาข่ายรูปหลายเหลี่ยมแต่ละขอบจะใช้ร่วมกันโดยไม่เกินสองรูปหลายเหลี่ยม ชุดของรูปหลายเหลี่ยมหรือใบหน้ารวมกันเป็น "ผิวหนัง" ของวัตถุ

วิธีนี้สามารถใช้เพื่อแสดงระดับของแข็ง / พื้นผิวในกราฟิกได้ ตาข่ายหลายเหลี่ยมสามารถแสดงผลได้โดยใช้อัลกอริธึมการกำจัดพื้นผิวที่ซ่อนอยู่ ตาข่ายรูปหลายเหลี่ยมสามารถแสดงได้สามวิธี -

• การแสดงที่ชัดเจน
• ชี้ไปที่รายการจุดยอด
• ชี้ไปที่รายการขอบ

ข้อดี

• สามารถใช้ในการจำลองวัตถุได้เกือบทุกชนิด
• ง่ายต่อการแสดงเป็นกลุ่มจุดยอด
• แปลงร่างได้ง่าย
• ง่ายต่อการวาดบนหน้าจอคอมพิวเตอร์

ข้อเสีย

• พื้นผิวโค้งสามารถอธิบายได้โดยประมาณเท่านั้น
• เป็นการยากที่จะจำลองวัตถุบางประเภทเช่นเส้นผมหรือของเหลว