คอมพิวเตอร์กราฟิก - คู่มือฉบับย่อ
คอมพิวเตอร์กราฟิกเป็นศิลปะการวาดภาพบนหน้าจอคอมพิวเตอร์ด้วยความช่วยเหลือของการเขียนโปรแกรม เกี่ยวข้องกับการคำนวณการสร้างและการจัดการข้อมูล กล่าวอีกนัยหนึ่งเราสามารถพูดได้ว่าคอมพิวเตอร์กราฟิกเป็นเครื่องมือในการแสดงผลสำหรับการสร้างและการจัดการภาพ
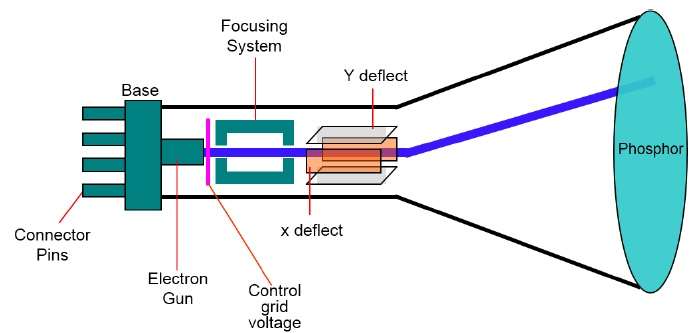
หลอดแคโทดเรย์
อุปกรณ์เอาต์พุตหลักในระบบกราฟิกคือจอภาพวิดีโอ องค์ประกอบหลักของจอภาพวิดีโอคือไฟล์Cathode Ray Tube (CRT), แสดงในภาพประกอบต่อไปนี้
การทำงานของ CRT นั้นง่ายมาก -
ปืนอิเล็กตรอนปล่อยลำแสงอิเล็กตรอน (รังสีแคโทด)
ลำแสงอิเล็กตรอนจะผ่านระบบโฟกัสและการเบี่ยงเบนที่นำไปยังตำแหน่งที่ระบุบนหน้าจอที่เคลือบสารเรืองแสง
เมื่อลำแสงกระทบหน้าจอสารเรืองแสงจะเปล่งแสงจุดเล็ก ๆ ในแต่ละตำแหน่งที่สัมผัสกับลำแสงอิเล็กตรอน
มันวาดภาพใหม่โดยนำลำแสงอิเล็กตรอนกลับไปที่จุดหน้าจอเดิมอย่างรวดเร็ว
มีสองวิธี (Random scan และ Raster scan) ซึ่งเราสามารถแสดงวัตถุบนหน้าจอได้
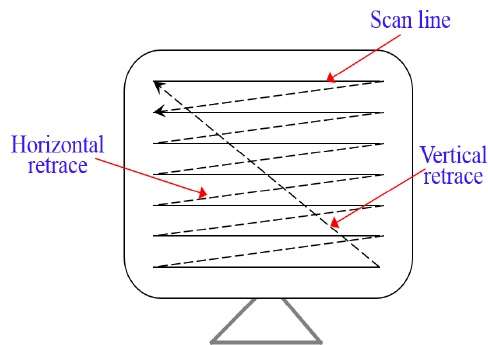
สแกนแรสเตอร์
ในระบบสแกนแรสเตอร์ลำแสงอิเล็กตรอนจะถูกกวาดผ่านหน้าจอทีละแถวจากบนลงล่าง เมื่อลำแสงอิเล็กตรอนเคลื่อนที่ผ่านแต่ละแถวความเข้มของลำแสงจะเปิดและปิดเพื่อสร้างรูปแบบของจุดที่ส่องสว่าง
นิยามรูปภาพจะถูกเก็บไว้ในพื้นที่หน่วยความจำที่เรียกว่า Refresh Buffer หรือ Frame Buffer. พื้นที่หน่วยความจำนี้เก็บชุดของค่าความเข้มสำหรับจุดหน้าจอทั้งหมด จากนั้นค่าความเข้มที่จัดเก็บไว้จะถูกดึงมาจากรีเฟรชบัฟเฟอร์และ "ทาสี" บนหน้าจอทีละแถว (เส้นสแกน) ตามที่แสดงในภาพประกอบต่อไปนี้
จุดหน้าจอแต่ละจุดเรียกว่าไฟล์ pixel (picture element) หรือ pel. ในตอนท้ายของแต่ละบรรทัดการสแกนลำแสงอิเล็กตรอนจะกลับไปที่ด้านซ้ายของหน้าจอเพื่อเริ่มแสดงบรรทัดการสแกนถัดไป
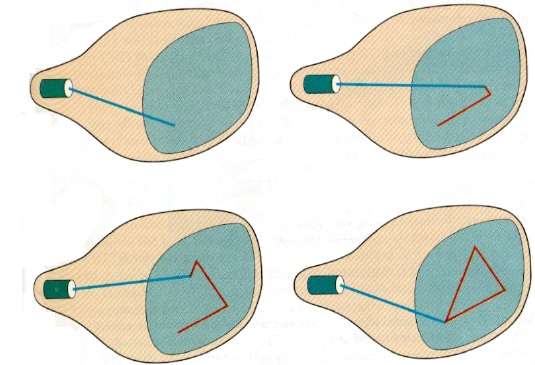
การสแกนแบบสุ่ม (การสแกนเวกเตอร์)
ในเทคนิคนี้ลำแสงอิเล็กตรอนจะถูกส่งไปยังส่วนของหน้าจอที่ต้องการวาดภาพเท่านั้นแทนที่จะสแกนจากซ้ายไปขวาและบนลงล่างเหมือนการสแกนแบบแรสเตอร์ เรียกอีกอย่างว่าvector display, stroke-writing display, หรือ calligraphic display.
นิยามรูปภาพจะถูกจัดเก็บเป็นชุดของคำสั่งการวาดเส้นในพื้นที่ของหน่วยความจำที่เรียกว่าไฟล์ refresh display file. ในการแสดงภาพที่ระบุระบบจะวนรอบชุดคำสั่งในไฟล์แสดงโดยวาดเส้นส่วนประกอบแต่ละเส้นตามลำดับ หลังจากประมวลผลคำสั่งวาดเส้นทั้งหมดแล้วระบบจะวนกลับไปที่คำสั่งบรรทัดแรกในรายการ
การสแกนแบบสุ่มได้รับการออกแบบมาเพื่อวาดเส้นส่วนประกอบทั้งหมดของภาพ 30 ถึง 60 ครั้งในแต่ละวินาที
การประยุกต์ใช้คอมพิวเตอร์กราฟิก
คอมพิวเตอร์กราฟิกมีแอพพลิเคชั่นมากมายซึ่งบางส่วนมีการระบุไว้ด้านล่าง -
Computer graphics user interfaces (GUIs) - กระบวนทัศน์กราฟิกที่เน้นเมาส์ซึ่งช่วยให้ผู้ใช้โต้ตอบกับคอมพิวเตอร์ได้
Business presentation graphics - "ภาพมีค่าพันคำ"
Cartography - วาดแผนที่
Weather Maps - การทำแผนที่แบบเรียลไทม์การแสดงสัญลักษณ์
Satellite Imaging - ภาพ Geodesic
Photo Enhancement - ปรับภาพเบลอให้คมชัด
Medical imaging - MRI, CAT scan ฯลฯ - การตรวจภายในแบบไม่รุกราน
Engineering drawings - เครื่องกลไฟฟ้าโยธา ฯลฯ - เปลี่ยนพิมพ์เขียวในอดีต
Typography - การใช้ภาพตัวละครในการเผยแพร่ - แทนที่ภาพพิมพ์ในอดีต
Architecture - แผนการก่อสร้างภาพร่างภายนอก - แทนที่พิมพ์เขียวและภาพวาดมือในอดีต
Art - คอมพิวเตอร์เป็นสื่อใหม่สำหรับศิลปิน
Training - เครื่องจำลองการบินคำสั่งโดยใช้คอมพิวเตอร์ช่วย ฯลฯ
Entertainment - ภาพยนตร์และเกม
Simulation and modeling - การแทนที่การสร้างแบบจำลองทางกายภาพและการออกกฎหมาย
เส้นเชื่อมต่อสองจุด มันเป็นองค์ประกอบพื้นฐานในกราฟิก ในการลากเส้นคุณต้องมีจุดสองจุดเพื่อลากเส้น ในสามอัลกอริทึมต่อไปนี้เราอ้างถึงจุดหนึ่งของบรรทัดว่า$X_{0}, Y_{0}$ และจุดที่สองของบรรทัดเป็น $X_{1}, Y_{1}$.
อัลกอริทึม DDA
อัลกอริทึม Digital Differential Analyzer (DDA) เป็นอัลกอริธึมการสร้างเส้นอย่างง่ายซึ่งอธิบายทีละขั้นตอนที่นี่
Step 1 - รับข้อมูลของจุดสิ้นสุดสองจุด $(X_{0}, Y_{0})$ และ $(X_{1}, Y_{1})$.
Step 2 - คำนวณความแตกต่างระหว่างสองจุดสิ้นสุด
dx = X1 - X0
dy = Y1 - Y0Step 3- จากความแตกต่างที่คำนวณได้ในขั้นตอนที่ 2 คุณต้องระบุจำนวนขั้นตอนในการใส่พิกเซล ถ้า dx> dy คุณต้องมีขั้นตอนเพิ่มเติมในพิกัด x มิฉะนั้นในพิกัด y
if (absolute(dx) > absolute(dy))
Steps = absolute(dx);
else
Steps = absolute(dy);Step 4 - คำนวณการเพิ่มขึ้นของพิกัด x และพิกัด y
Xincrement = dx / (float) steps;
Yincrement = dy / (float) steps;Step 5 - ใส่พิกเซลโดยเพิ่มพิกัด x และ y ให้สำเร็จตามลำดับและวาดเส้นให้สมบูรณ์
for(int v=0; v < Steps; v++)
{
x = x + Xincrement;
y = y + Yincrement;
putpixel(Round(x), Round(y));
}Line Generation ของ Bresenham
อัลกอริทึม Bresenham เป็นอีกหนึ่งอัลกอริทึมการแปลงการสแกนที่เพิ่มขึ้น ข้อได้เปรียบที่สำคัญของอัลกอริทึมนี้คือใช้การคำนวณจำนวนเต็มเท่านั้น การเคลื่อนที่ข้ามแกน x ในช่วงเวลาของหน่วยและในแต่ละขั้นตอนให้เลือกระหว่างพิกัด y สองพิกัดที่ต่างกัน
ตัวอย่างเช่นดังที่แสดงในภาพประกอบต่อไปนี้จากตำแหน่ง (2, 3) คุณต้องเลือกระหว่าง (3, 3) และ (3, 4) คุณต้องการจุดที่ใกล้กับเส้นเดิมมากขึ้น
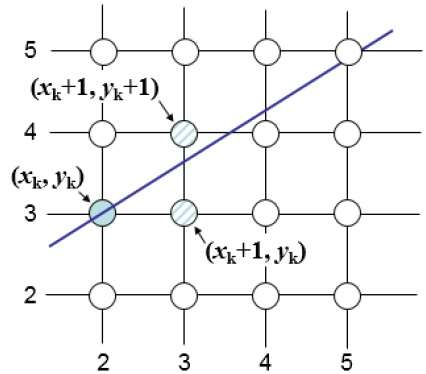
ที่ตำแหน่งตัวอย่าง $X_{k}+1,$ การแยกแนวตั้งจากเส้นคณิตศาสตร์มีข้อความระบุว่า $d_{upper}$ และ $d_{lower}$.
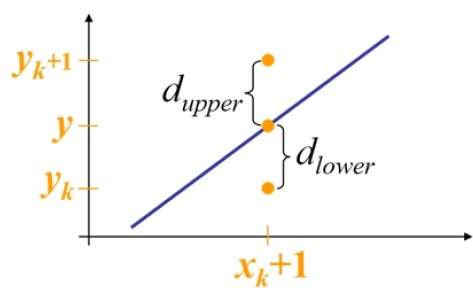
จากภาพประกอบด้านบนพิกัด y บนเส้นคณิตศาสตร์ที่ $x_{k}+1$ คือ -
Y = ม. ($X_{k}$+1) + b
ดังนั้น, $d_{upper}$ และ $d_{lower}$ ได้รับดังต่อไปนี้ -
$$d_{lower} = y-y_{k}$$
$$= m(X_{k} + 1) + b - Y_{k}$$
และ
$$d_{upper} = (y_{k} + 1) - y$$
$= Y_{k} + 1 - m (X_{k} + 1) - b$
คุณสามารถใช้สิ่งเหล่านี้ในการตัดสินใจง่ายๆว่าพิกเซลใดอยู่ใกล้เส้นคณิตศาสตร์มากขึ้น การตัดสินใจง่ายๆนี้ขึ้นอยู่กับความแตกต่างระหว่างตำแหน่งพิกเซลทั้งสอง
$$d_{lower} - d_{upper} = 2m(x_{k} + 1) - 2y_{k} + 2b - 1$$
ให้เราแทนที่mด้วยdy / dxโดยที่dxและdyคือความแตกต่างระหว่างจุดสิ้นสุด
$$dx (d_{lower} - d_{upper}) =dx(2\frac{\mathrm{d} y}{\mathrm{d} x}(x_{k} + 1) - 2y_{k} + 2b - 1)$$
$$ = 2dy.x_{k} - 2dx.y_{k} + 2dy + 2dx(2b-1)$$
$$ = 2dy.x_{k} - 2dx.y_{k} + C$$
ดังนั้นพารามิเตอร์การตัดสินใจ $P_{k}$สำหรับขั้นตอนที่kตามเส้นกำหนดโดย -
$$p_{k} = dx(d_{lower} - d_{upper})$$
$$ = 2dy.x_{k} - 2dx.y_{k} + C$$
สัญลักษณ์ของพารามิเตอร์การตัดสินใจ $P_{k}$ เหมือนกับของ $d_{lower} - d_{upper}$.
ถ้า $p_{k}$ เป็นลบจากนั้นเลือกพิกเซลที่ต่ำกว่าหรือเลือกพิกเซลบน
โปรดจำไว้ว่าการเปลี่ยนแปลงพิกัดเกิดขึ้นตามแกน x ในหน่วยขั้นตอนดังนั้นคุณสามารถทำทุกอย่างได้ด้วยการคำนวณจำนวนเต็ม ในขั้นตอนที่ k + 1 พารามิเตอร์การตัดสินใจถูกกำหนดเป็น -
$$p_{k +1} = 2dy.x_{k + 1} - 2dx.y_{k + 1} + C$$
การลบ $p_{k}$ จากสิ่งนี้เราได้รับ -
$$p_{k + 1} - p_{k} = 2dy(x_{k + 1} - x_{k}) - 2dx(y_{k + 1} - y_{k})$$
แต่, $x_{k+1}$ เหมือนกับ $x_{k+1}$. ดังนั้น -
$$p_{k+1} = p_{k} + 2dy - 2dx(y_{k+1} - y_{k})$$
ที่ไหน $Y_{k+1} – Y_{k}$ เป็น 0 หรือ 1 ขึ้นอยู่กับสัญลักษณ์ของ $P_{k}$.
พารามิเตอร์การตัดสินใจแรก $p_{0}$ ได้รับการประเมินที่ $(x_{0}, y_{0})$ ได้รับเป็น -
$$p_{0} = 2dy - dx$$
ตอนนี้โปรดทราบถึงประเด็นข้างต้นและการคำนวณทั้งหมดนี่คืออัลกอริทึม Bresenham สำหรับความชัน m <1 -
Step 1 - ป้อนจุดสิ้นสุดของเส้นสองจุดโดยจัดเก็บจุดปลายด้านซ้ายใน $(x_{0}, y_{0})$.
Step 2 - พล็อตประเด็น $(x_{0}, y_{0})$.
Step 3 - คำนวณค่าคงที่ dx, dy, 2dy และ (2dy - 2dx) และรับค่าแรกสำหรับพารามิเตอร์การตัดสินใจเป็น -
$$p_{0} = 2dy - dx$$
Step 4 - ในแต่ละครั้ง $X_{k}$ ตามแนวเริ่มต้นที่ k = 0 ทำการทดสอบต่อไปนี้ -
ถ้า $p_{k}$ <0 จุดต่อไปที่จะลงจุดคือ $(x_{k}+1, y_{k})$ และ
$$p_{k+1} = p_{k} + 2dy$$ มิฉะนั้น,
$$(x_{k}, y_{k}+1)$$
$$p_{k+1} = p_{k} + 2dy - 2dx$$
Step 5 - ทำซ้ำขั้นตอนที่ 4 (dx - 1) ครั้ง
สำหรับ m> 1 ให้ค้นหาว่าคุณต้องเพิ่ม x ในขณะที่เพิ่ม y ทุกครั้งหรือไม่
หลังจากแก้สมการสำหรับพารามิเตอร์การตัดสินใจ $P_{k}$ จะใกล้เคียงกันมากเพียงแค่ x และ y ในสมการได้รับการแลกเปลี่ยนกัน
อัลกอริทึมจุดกึ่งกลาง
อัลกอริทึมจุดกึ่งกลางเกิดจาก Bresenham ซึ่งแก้ไขโดย Pitteway และ Van Aken สมมติว่าคุณได้ใส่จุด P ไว้ที่พิกัด (x, y) แล้วและความชันของเส้นคือ 0 ≤ k ≤ 1 ดังแสดงในภาพประกอบต่อไปนี้
ตอนนี้คุณต้องตัดสินใจว่าจะวางจุดต่อไปที่ E หรือ N ซึ่งสามารถเลือกได้โดยการระบุจุดตัดกัน Q ใกล้กับจุด N หรือ E มากที่สุดหากจุดตัดกัน Q อยู่ใกล้กับจุด N มากที่สุดดังนั้น N จะถือว่าเป็น จุดต่อไป; มิฉะนั้น E.
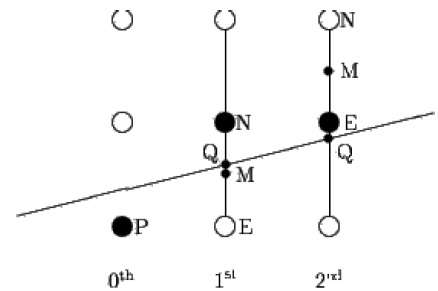
ก่อนอื่นให้คำนวณจุดกลาง M (x + 1, y + ½) ถ้าจุดตัดกัน Q ของเส้นที่มีเส้นแนวตั้งเชื่อมต่อ E และ N อยู่ต่ำกว่า M ให้ใช้ E เป็นจุดถัดไป มิฉะนั้นจะใช้ N เป็นจุดถัดไป
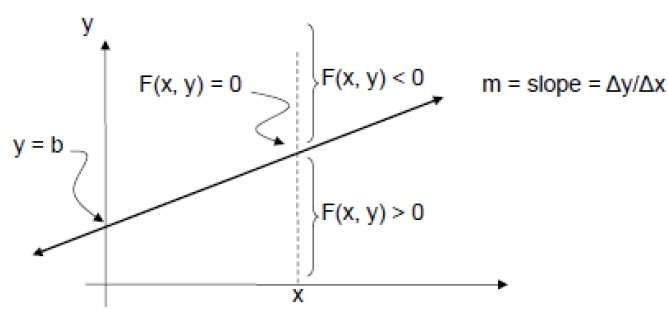
ในการตรวจสอบสิ่งนี้เราต้องพิจารณาสมการนัย -
F (x, y) = mx + b - y
สำหรับม. บวกที่ X ที่กำหนด
- ถ้า y อยู่บนเส้นแล้ว F (x, y) = 0
- ถ้า y อยู่เหนือเส้นแล้ว F (x, y) <0
- ถ้า y อยู่ต่ำกว่าเส้นแล้ว F (x, y)> 0
การวาดวงกลมบนหน้าจอนั้นซับซ้อนกว่าการวาดเส้นเล็กน้อย มีอัลกอริทึมยอดนิยมสองแบบในการสร้างวงกลม -Bresenham’s Algorithm และ Midpoint Circle Algorithm. อัลกอริทึมเหล่านี้ขึ้นอยู่กับแนวคิดในการกำหนดจุดต่อมาที่จำเป็นในการวาดวงกลม ให้เราหารือเกี่ยวกับอัลกอริทึมโดยละเอียด -
สมการของวงกลมคือ $X^{2} + Y^{2} = r^{2},$ โดยที่ r คือรัศมี
อัลกอริทึมของ Bresenham
เราไม่สามารถแสดงส่วนโค้งต่อเนื่องบนจอแสดงผลแบบแรสเตอร์ได้ แต่เราต้องเลือกตำแหน่งพิกเซลที่ใกล้ที่สุดเพื่อให้ส่วนโค้งสมบูรณ์
จากภาพประกอบต่อไปนี้คุณจะเห็นว่าเราวางพิกเซลไว้ที่ตำแหน่ง (X, Y) และตอนนี้ต้องตัดสินใจว่าจะวางพิกเซลต่อไปที่ใด - ที่ N (X + 1, Y) หรือที่ S (X + 1, Y-1)
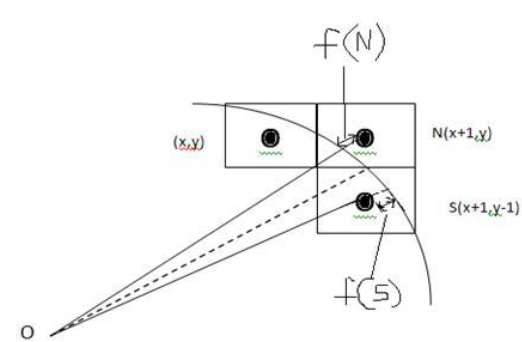
สิ่งนี้สามารถตัดสินใจได้โดยพารามิเตอร์การตัดสินใจ d.
- ถ้า d <= 0 ดังนั้น N (X + 1, Y) จะถูกเลือกเป็นพิกเซลถัดไป
- ถ้า d> 0 ดังนั้น S (X + 1, Y-1) จะถูกเลือกเป็นพิกเซลถัดไป
อัลกอริทึม
Step 1- รับพิกัดของจุดศูนย์กลางของวงกลมและรัศมีแล้วเก็บไว้ใน x, y และ R ตามลำดับ ตั้งค่า P = 0 และ Q = R
Step 2 - ตั้งค่าพารามิเตอร์การตัดสินใจ D = 3 - 2R
Step 3 - ทำซ้ำถึงขั้นตอนที่ -8 ในขณะที่ P ≤ Q.
Step 4 - โทรวาดวงกลม (X, Y, P, Q)
Step 5 - เพิ่มมูลค่าของ P.
Step 6 - ถ้า D <0 แล้ว D = D + 4P + 6
Step 7 - ชุดอื่น R = R - 1, D = D + 4 (PQ) + 10
Step 8 - โทรวาดวงกลม (X, Y, P, Q)
Draw Circle Method(X, Y, P, Q).
Call Putpixel (X + P, Y + Q).
Call Putpixel (X - P, Y + Q).
Call Putpixel (X + P, Y - Q).
Call Putpixel (X - P, Y - Q).
Call Putpixel (X + Q, Y + P).
Call Putpixel (X - Q, Y + P).
Call Putpixel (X + Q, Y - P).
Call Putpixel (X - Q, Y - P).อัลกอริทึมจุดกึ่งกลาง
Step 1 - รัศมีอินพุต r และศูนย์วงกลม $(x_{c,} y_{c})$ และรับจุดแรกบนเส้นรอบวงของวงกลมที่มีศูนย์กลางอยู่ที่จุดกำเนิดเป็น
(x0, y0) = (0, r)Step 2 - คำนวณค่าเริ่มต้นของพารามิเตอร์การตัดสินใจเป็น
$P_{0}$ = 5/4 - r (ดูคำอธิบายต่อไปนี้สำหรับการทำให้สมการนี้ง่ายขึ้น)
f(x, y) = x2 + y2 - r2 = 0
f(xi - 1/2 + e, yi + 1)
= (xi - 1/2 + e)2 + (yi + 1)2 - r2
= (xi- 1/2)2 + (yi + 1)2 - r2 + 2(xi - 1/2)e + e2
= f(xi - 1/2, yi + 1) + 2(xi - 1/2)e + e2 = 0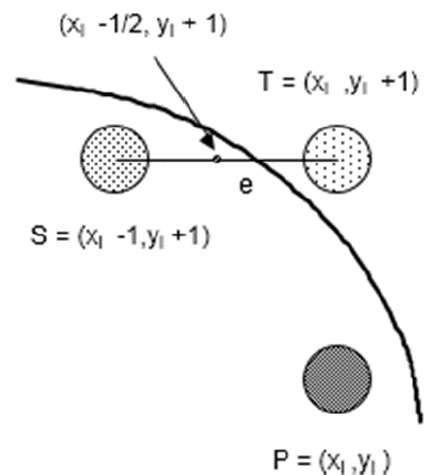
Let di = f(xi - 1/2, yi + 1) = -2(xi - 1/2)e - e2
Thus,
If e < 0 then di > 0 so choose point S = (xi - 1, yi + 1).
di+1 = f(xi - 1 - 1/2, yi + 1 + 1) = ((xi - 1/2) - 1)2 + ((yi + 1) + 1)2 - r2
= di - 2(xi - 1) + 2(yi + 1) + 1
= di + 2(yi + 1 - xi + 1) + 1
If e >= 0 then di <= 0 so choose point T = (xi, yi + 1)
di+1 = f(xi - 1/2, yi + 1 + 1)
= di + 2yi+1 + 1
The initial value of di is
d0 = f(r - 1/2, 0 + 1) = (r - 1/2)2 + 12 - r2
= 5/4 - r {1-r can be used if r is an integer}
When point S = (xi - 1, yi + 1) is chosen then
di+1 = di + -2xi+1 + 2yi+1 + 1
When point T = (xi, yi + 1) is chosen then
di+1 = di + 2yi+1 + 1Step 3 - ในแต่ละครั้ง $X_{K}$ ตำแหน่งเริ่มต้นที่ K = 0 ทำการทดสอบต่อไปนี้ -
If PK < 0 then next point on circle (0,0) is (XK+1,YK) and
PK+1 = PK + 2XK+1 + 1
Else
PK+1 = PK + 2XK+1 + 1 – 2YK+1
Where, 2XK+1 = 2XK+2 and 2YK+1 = 2YK-2.Step 4 - กำหนดจุดสมมาตรในอีกเจ็ดแปด
Step 5 - ย้ายตำแหน่งพิกเซลคำนวณ (X, Y) ไปยังเส้นทางวงกลมที่อยู่ตรงกลาง $(X_{C,} Y_{C})$ และพล็อตค่าพิกัด
X = X + XC, Y = Y + YCStep 6 - ทำซ้ำขั้นตอนที่ 3 ถึง 5 จนถึง X> = Y
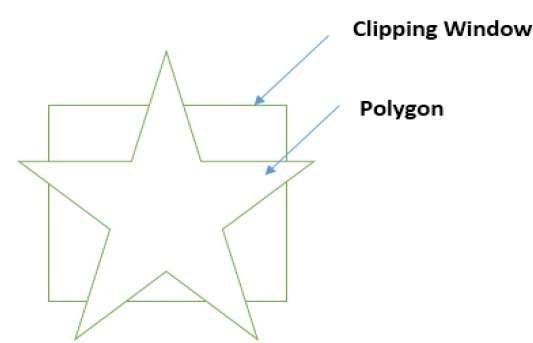
รูปหลายเหลี่ยมคือรายการลำดับของจุดยอดดังแสดงในรูปต่อไปนี้ สำหรับการเติมรูปหลายเหลี่ยมด้วยสีเฉพาะคุณต้องกำหนดพิกเซลที่ตกลงบนขอบของรูปหลายเหลี่ยมและพิกเซลที่อยู่ภายในรูปหลายเหลี่ยม ในบทนี้เราจะมาดูวิธีเติมรูปหลายเหลี่ยมโดยใช้เทคนิคต่างๆ

Scan Line Algorithm
อัลกอริทึมนี้ทำงานโดยการตัดเส้นแสกนไลน์กับขอบรูปหลายเหลี่ยมและเติมรูปหลายเหลี่ยมระหว่างจุดตัดคู่ ขั้นตอนต่อไปนี้แสดงให้เห็นว่าอัลกอริทึมนี้ทำงานอย่างไร
Step 1 - ค้นหา Ymin และ Ymax จากรูปหลายเหลี่ยมที่กำหนด
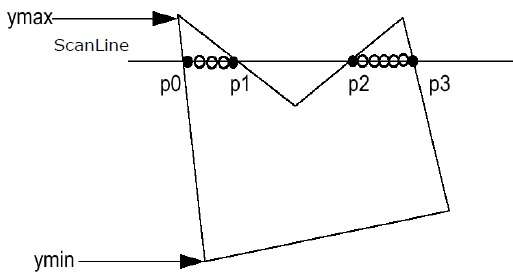
Step 2- ScanLine ตัดกับขอบแต่ละด้านของรูปหลายเหลี่ยมจาก Ymin ถึง Ymax ตั้งชื่อจุดตัดกันของรูปหลายเหลี่ยมแต่ละจุด ตามรูปที่แสดงด้านบนมีชื่อเป็น p0, p1, p2, p3
Step 3 - เรียงลำดับจุดตัดตามลำดับที่เพิ่มขึ้นของพิกัด X ได้แก่ (p0, p1), (p1, p2) และ (p2, p3)
Step 4 - กรอกคู่พิกัดทั้งหมดที่อยู่ภายในรูปหลายเหลี่ยมและละเว้นคู่อื่น
อัลกอริทึมการเติมน้ำท่วม
บางครั้งเราเจอวัตถุที่ต้องการเติมเต็มพื้นที่และขอบเขตของมันด้วยสีที่ต่างกัน เราสามารถทาสีวัตถุดังกล่าวด้วยสีภายในที่ระบุแทนการค้นหาสีขอบเขตเฉพาะเช่นเดียวกับอัลกอริทึมการเติมขอบเขต
แทนที่จะอาศัยขอบเขตของวัตถุ แต่อาศัยสีเติม กล่าวอีกนัยหนึ่งคือแทนที่สีภายในของวัตถุด้วยสีเติม เมื่อไม่มีพิกเซลของสีภายในดั้งเดิมอีกต่อไปอัลกอริทึมจะเสร็จสมบูรณ์
อีกครั้งอัลกอริทึมนี้อาศัยวิธีการเชื่อมต่อแบบ Four-connect หรือ Eight-connect ในการเติมพิกเซล แต่แทนที่จะมองหาสีขอบเขตจะมองหาพิกเซลที่อยู่ติดกันทั้งหมดที่เป็นส่วนหนึ่งของการตกแต่งภายใน
อัลกอริทึมการเติมขอบเขต
อัลกอริทึมการเติมขอบเขตทำงานเป็นชื่อของมัน อัลกอริทึมนี้เลือกจุดภายในวัตถุและเริ่มเติมจนกว่าจะถึงขอบเขตของวัตถุ สีของขอบเขตและสีที่เราเติมควรแตกต่างกันเพื่อให้อัลกอริทึมนี้ทำงานได้
ในอัลกอริทึมนี้เราถือว่าสีของขอบเขตนั้นเหมือนกันสำหรับวัตถุทั้งหมด อัลกอริทึมการเติมขอบเขตสามารถใช้งานได้โดยพิกเซลที่เชื่อมต่อ 4 พิกเซลหรือพิกเซลที่เชื่อมต่อ 8 พิกเซล
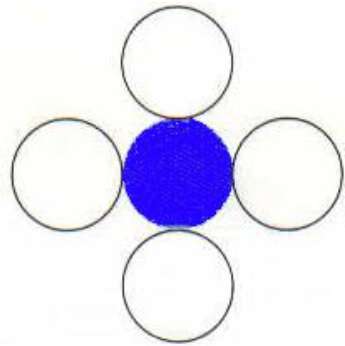
รูปหลายเหลี่ยมที่เชื่อมต่อ 4 รูปแบบ
ในเทคนิคนี้ใช้พิกเซลที่เชื่อมต่อ 4 จุดดังแสดงในรูป เรากำลังวางพิกเซลด้านบนด้านล่างไปทางขวาและทางด้านซ้ายของพิกเซลปัจจุบันและกระบวนการนี้จะดำเนินต่อไปจนกว่าเราจะพบขอบเขตที่มีสีแตกต่างกัน
อัลกอริทึม
Step 1 - เริ่มต้นค่าของ seed point (seedx, seedy), fcolor และ dcol
Step 2 - กำหนดค่าขอบเขตของรูปหลายเหลี่ยม
Step 3 - ตรวจสอบว่าจุดเริ่มต้นปัจจุบันเป็นสีเริ่มต้นหรือไม่จากนั้นทำซ้ำขั้นตอนที่ 4 และ 5 จนกระทั่งถึงพิกเซลขอบเขต
If getpixel(x, y) = dcol then repeat step 4 and 5Step 4 - เปลี่ยนสีเริ่มต้นด้วยสีเติมที่จุดเริ่มต้น
setPixel(seedx, seedy, fcol)Step 5 - ทำตามขั้นตอนซ้ำ ๆ โดยมีจุดใกล้เคียงสี่จุด
FloodFill (seedx – 1, seedy, fcol, dcol)
FloodFill (seedx + 1, seedy, fcol, dcol)
FloodFill (seedx, seedy - 1, fcol, dcol)
FloodFill (seedx – 1, seedy + 1, fcol, dcol)Step 6 - ออก
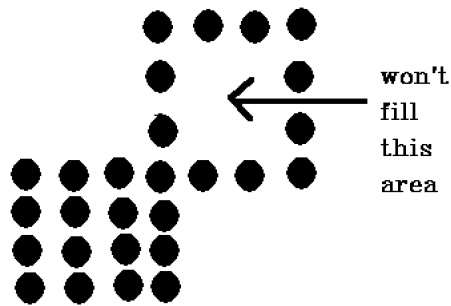
มีปัญหากับเทคนิคนี้ พิจารณากรณีดังที่แสดงด้านล่างที่เราพยายามเติมเต็มทั้งภูมิภาค ที่นี่ภาพจะเต็มไปเพียงบางส่วน ในกรณีเช่นนี้ไม่สามารถใช้เทคนิค 4-connected pixels ได้
รูปหลายเหลี่ยมที่เชื่อมต่อกัน 8 รูป
ในเทคนิคนี้จะใช้พิกเซลที่เชื่อมต่อกัน 8 พิกเซลดังแสดงในรูป เรากำลังวางพิกเซลไว้ด้านบนด้านล่างด้านขวาและด้านซ้ายของพิกเซลปัจจุบันตามที่เราทำในเทคนิค 4-connected
นอกจากนี้เรายังวางพิกเซลในแนวทแยงมุมเพื่อให้ครอบคลุมพื้นที่ทั้งหมดของพิกเซลปัจจุบัน กระบวนการนี้จะดำเนินต่อไปจนกว่าเราจะพบขอบเขตที่มีสีต่างกัน

อัลกอริทึม
Step 1 - เริ่มต้นค่าของ seed point (seedx, seedy), fcolor และ dcol
Step 2 - กำหนดค่าขอบเขตของรูปหลายเหลี่ยม
Step 3 - ตรวจสอบว่าจุดเริ่มต้นปัจจุบันเป็นสีเริ่มต้นหรือไม่จากนั้นทำซ้ำขั้นตอนที่ 4 และ 5 จนกระทั่งถึงพิกเซลขอบเขต
If getpixel(x,y) = dcol then repeat step 4 and 5Step 4 - เปลี่ยนสีเริ่มต้นด้วยสีเติมที่จุดเริ่มต้น
setPixel(seedx, seedy, fcol)Step 5 - ทำตามขั้นตอนซ้ำ ๆ โดยมีจุดใกล้เคียงสี่จุด
FloodFill (seedx – 1, seedy, fcol, dcol)
FloodFill (seedx + 1, seedy, fcol, dcol)
FloodFill (seedx, seedy - 1, fcol, dcol)
FloodFill (seedx, seedy + 1, fcol, dcol)
FloodFill (seedx – 1, seedy + 1, fcol, dcol)
FloodFill (seedx + 1, seedy + 1, fcol, dcol)
FloodFill (seedx + 1, seedy - 1, fcol, dcol)
FloodFill (seedx – 1, seedy - 1, fcol, dcol)Step 6 - ออก
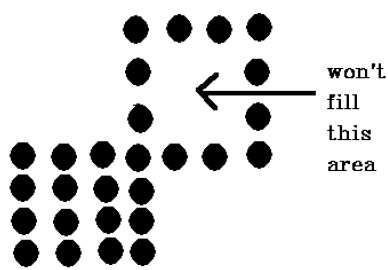
เทคนิคพิกเซลที่เชื่อมต่อ 4 จุดล้มเหลวในการเติมเต็มพื้นที่ตามที่ระบุไว้ในรูปต่อไปนี้ซึ่งจะไม่เกิดขึ้นกับเทคนิค 8-connected
การทดสอบภายใน - ภายนอก
วิธีนี้เรียกอีกอย่างว่า counting number method. ในขณะเติมวัตถุเรามักจะต้องระบุว่าจุดใดจุดหนึ่งอยู่ภายในวัตถุหรือภายนอกวัตถุนั้น มีสองวิธีที่เราสามารถระบุได้ว่าจุดใดจุดหนึ่งอยู่ภายในวัตถุหรือภายนอก
- กฎคี่ - คู่
- กฎเลขที่คดเคี้ยวไม่ใช่ศูนย์
กฎคี่ - คู่
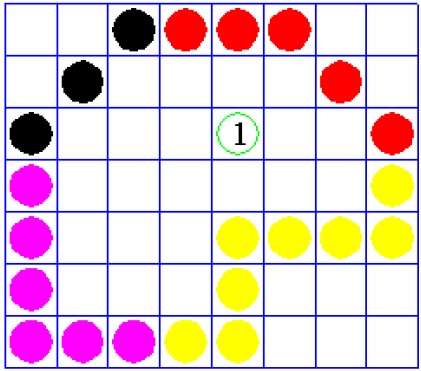
ในเทคนิคนี้เรานับการข้ามขอบตามเส้นจากจุดใด ๆ (x, y) ถึงอินฟินิตี้ ถ้าจำนวนการโต้ตอบเป็นเลขคี่จุด (x, y) จะเป็นจุดภายใน ถ้าจำนวนการโต้ตอบเท่ากันจุด (x, y) คือจุดภายนอก นี่คือตัวอย่างเพื่อให้คุณมีแนวคิดที่ชัดเจน -
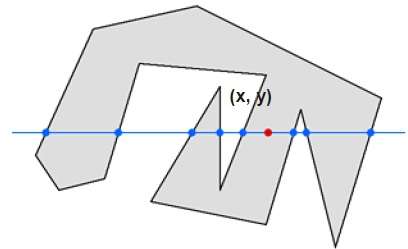
จากรูปด้านบนเราจะเห็นว่าจากจุด (x, y) จำนวนจุดปฏิสัมพันธ์ทางด้านซ้ายคือ 5 และทางด้านขวาคือ 3 ดังนั้นจำนวนจุดปฏิสัมพันธ์ทั้งหมดคือ 8 ซึ่งเป็นเลขคี่ . ดังนั้นจุดจะถูกพิจารณาภายในวัตถุ
กฎเลขที่คดเคี้ยวที่ไม่ใช่ศูนย์
วิธีนี้ยังใช้กับรูปหลายเหลี่ยมอย่างง่ายเพื่อทดสอบจุดที่ระบุว่าอยู่ภายในหรือไม่ สามารถเข้าใจได้ง่ายๆด้วยความช่วยเหลือของหมุดและแถบยาง ยึดหมุดที่ขอบด้านใดด้านหนึ่งของรูปหลายเหลี่ยมแล้วมัดแถบยางเข้าด้วยกันจากนั้นยืดแถบยางตามขอบของรูปหลายเหลี่ยม
เมื่อขอบทั้งหมดของรูปหลายเหลี่ยมถูกรัดด้วยแถบยางให้ตรวจสอบหมุดที่ยึดไว้ตรงจุดที่จะทดสอบ ถ้าเราพบลมอย่างน้อยหนึ่งจุดให้พิจารณาภายในรูปหลายเหลี่ยมมิฉะนั้นเราสามารถพูดได้ว่าจุดนั้นไม่ได้อยู่ในรูปหลายเหลี่ยม
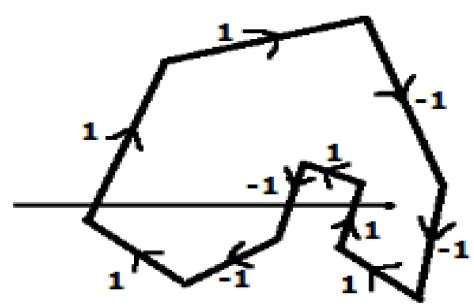
ในวิธีอื่นให้บอกทิศทางไปยังขอบทั้งหมดของรูปหลายเหลี่ยม ลากเส้นสแกนจากจุดที่จะทดสอบไปทางซ้ายสุดของทิศทาง X
ให้ค่า 1 กับขอบทั้งหมดซึ่งกำลังจะขึ้นไปและ -1 อื่น ๆ ทั้งหมดเป็นค่าทิศทาง
ตรวจสอบค่าทิศทางขอบที่เส้นสแกนกำลังผ่านและสรุปผล
หากผลรวมทั้งหมดของค่าทิศทางนี้ไม่เป็นศูนย์จุดที่จะทดสอบนี้คือ interior point, มิฉะนั้นจะเป็นไฟล์ exterior point.
ในรูปด้านบนเราสรุปค่าทิศทางที่เส้นสแกนกำลังผ่านจากนั้นผลรวมคือ 1 - 1 + 1 = 1; ซึ่งไม่ใช่ศูนย์ ดังนั้นจุดที่กล่าวว่าเป็นจุดภายใน
การใช้การตัดแบบหลักในคอมพิวเตอร์กราฟิกคือการลบวัตถุเส้นหรือส่วนของเส้นที่อยู่นอกบานหน้าต่างการดู การเปลี่ยนแปลงการรับชมไม่ไวต่อตำแหน่งของจุดที่สัมพันธ์กับปริมาณการรับชม - โดยเฉพาะจุดที่อยู่ด้านหลังของผู้ชม - และจำเป็นต้องลบจุดเหล่านี้ออกก่อนที่จะสร้างมุมมอง
การตัดจุด
การตัดจุดจากหน้าต่างที่กำหนดนั้นง่ายมาก พิจารณารูปต่อไปนี้โดยที่สี่เหลี่ยมผืนผ้าระบุหน้าต่าง การตัดจุดบอกเราว่าจุดที่กำหนด (X, Y) อยู่ในหน้าต่างที่กำหนดหรือไม่ และตัดสินใจว่าเราจะใช้พิกัดต่ำสุดและสูงสุดของหน้าต่างหรือไม่
พิกัด X ของจุดที่กำหนดอยู่ภายในหน้าต่างถ้า X อยู่ระหว่าง Wx1 ≤ X ≤ Wx2 ในทำนองเดียวกันพิกัด Y ของจุดที่กำหนดอยู่ภายในหน้าต่างถ้า Y อยู่ระหว่าง Wy1 ≤ Y ≤ Wy2

การตัดเส้น
แนวคิดของการตัดเส้นเหมือนกับการตัดจุด ในการตัดบรรทัดเราจะตัดส่วนของเส้นที่อยู่นอกหน้าต่างและเก็บเฉพาะส่วนที่อยู่ในหน้าต่างเท่านั้น
คลิปสายโคเฮน - ซัทเทอร์แลนด์
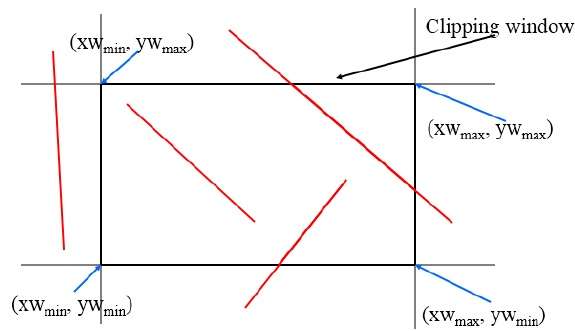
อัลกอริทึมนี้ใช้หน้าต่างการตัดตามที่แสดงในรูปต่อไปนี้ พิกัดขั้นต่ำสำหรับพื้นที่การตัดคือ$(XW_{min,} YW_{min})$ และพิกัดสูงสุดสำหรับพื้นที่การตัดคือ $(XW_{max,} YW_{max})$.
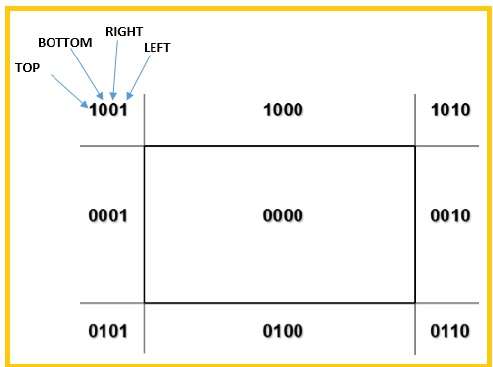
เราจะใช้ 4 บิตเพื่อแบ่งภูมิภาคทั้งหมด 4 บิตเหล่านี้แสดงถึงด้านบนล่างขวาและซ้ายของพื้นที่ดังแสดงในรูปต่อไปนี้ ที่นี่TOP และ LEFT บิตถูกตั้งค่าเป็น 1 เนื่องจากเป็นไฟล์ TOP-LEFT มุม.
มีความเป็นไปได้ 3 สาย -
เส้นสามารถอยู่ในหน้าต่างได้อย่างสมบูรณ์ (ควรยอมรับบรรทัดนี้)
เส้นสามารถอยู่นอกหน้าต่างได้อย่างสมบูรณ์ (บรรทัดนี้จะถูกลบออกจากพื้นที่โดยสิ้นเชิง)
เส้นสามารถอยู่ภายในหน้าต่างได้บางส่วน (เราจะพบจุดตัดกันและวาดเฉพาะส่วนของเส้นที่อยู่ในพื้นที่)
อัลกอริทึม
Step 1 - กำหนดรหัสภูมิภาคสำหรับแต่ละจุดสิ้นสุด
Step 2 - หากปลายทางทั้งสองมีรหัสภูมิภาค 0000 จากนั้นยอมรับบรรทัดนี้
Step 3 - อื่น ๆ ดำเนินการตามตรรกะ ANDการดำเนินการสำหรับรหัสภูมิภาคทั้งสอง
Step 3.1 - หากผลลัพธ์ไม่เป็น 0000, จากนั้นปฏิเสธสาย
Step 3.2 - อย่างอื่นคุณต้องตัด
Step 3.2.1 - เลือกจุดสิ้นสุดของเส้นที่อยู่นอกหน้าต่าง
Step 3.2.2 - ค้นหาจุดตัดที่ขอบหน้าต่าง (ตามรหัสภูมิภาค)
Step 3.2.3 - แทนที่จุดสิ้นสุดด้วยจุดตัดกันและอัปเดตรหัสภูมิภาค
Step 3.2.4 - ทำซ้ำขั้นตอนที่ 2 จนกว่าเราจะพบเส้นที่ถูกตัดออกว่าได้รับการยอมรับเล็กน้อยหรือปฏิเสธเล็กน้อย
Step 4 - ทำซ้ำขั้นตอนที่ 1 สำหรับบรรทัดอื่น ๆ
Cyrus-Beck Line Clipping Algorithm
อัลกอริทึมนี้มีประสิทธิภาพสูงกว่าอัลกอริทึม Cohen-Sutherland ใช้การแสดงเส้นพาราเมตริกและผลิตภัณฑ์ดอทอย่างง่าย
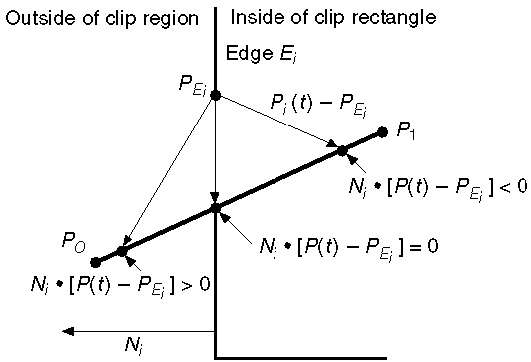
สมการเชิงพาราเมตริกของเส้นคือ -
P0P1:P(t) = P0 + t(P1-P0)ให้ N ฉันเป็นคนปกติออกไปด้านนอกขอบ E ฉัน ตอนนี้เลือกจุดใดก็ได้ตามอำเภอใจ P Eiบนขอบ E iจากนั้นผลิตภัณฑ์ดอท N i ∙ [P (t) - P Ei ] กำหนดว่าจุด P (t) อยู่“ ภายในขอบคลิป” หรือ“ นอก” ขอบคลิปหรือ "เปิด" ขอบคลิป
จุด P (t) อยู่ภายในถ้า N i [P (t) - P Ei ] <0
จุด P (t) อยู่นอกถ้า N i . [P (t) - P Ei ]> 0
จุด P (t) อยู่ที่ขอบถ้า N i . [P (t) - P Ei ] = 0 (จุดตัด)
N ฉัน . [P (t) - P Ei ] = 0
N i . [P 0 + t (P 1 -P 0 ) - P Ei ] = 0 (การแทนที่ P (t) ด้วย P 0 + t (P 1 -P 0 ))
N i . [P 0 - P Ei ] + N i .t [P 1 -P 0 ] = 0
N i . [P 0 - P Ei ] + N i ∙ tD = 0 (แทนที่ D สำหรับ [P 1 -P 0 ])
N i . [P 0 - P Ei ] = - N i ∙ tD
สมการของ t กลายเป็น
$$t = \tfrac{N_{i}.[P_{o} - P_{Ei}]}{{- N_{i}.D}}$$
ใช้ได้กับเงื่อนไขต่อไปนี้ -
- N i ≠ 0 (ข้อผิดพลาดไม่สามารถเกิดขึ้นได้)
- D ≠ 0 (P 1 ≠ P 0 )
- N i ∙ D ≠ 0 (P 0 P 1ไม่ขนานกับ E i )
รูปหลายเหลี่ยม (Sutherland Hodgman Algorithm)
นอกจากนี้ยังสามารถตัดรูปหลายเหลี่ยมได้โดยระบุหน้าต่างการตัด อัลกอริทึมการตัดรูปหลายเหลี่ยมของ Sutherland Hodgeman ใช้สำหรับการตัดรูปหลายเหลี่ยม ในอัลกอริทึมนี้จุดยอดทั้งหมดของรูปหลายเหลี่ยมจะถูกตัดกับขอบแต่ละด้านของหน้าต่างการตัด
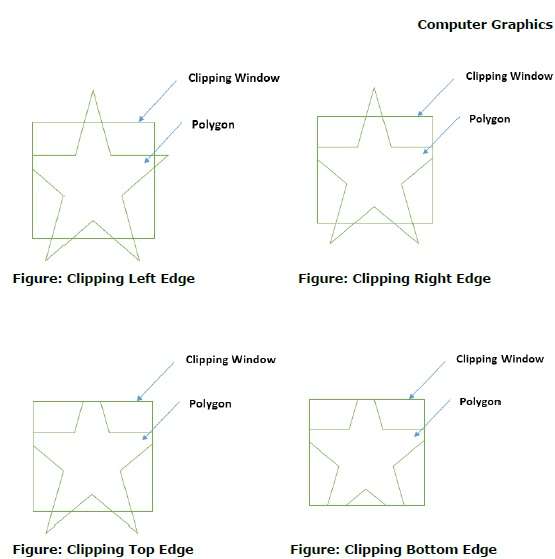
ขั้นแรกให้รูปหลายเหลี่ยมถูกตัดชิดขอบด้านซ้ายของหน้าต่างรูปหลายเหลี่ยมเพื่อให้ได้จุดยอดใหม่ของรูปหลายเหลี่ยม จุดยอดใหม่เหล่านี้ใช้เพื่อตัดรูปหลายเหลี่ยมกับขอบด้านขวาขอบด้านบนขอบด้านล่างของหน้าต่างคลิปดังแสดงในรูปต่อไปนี้
ในขณะที่ประมวลผลขอบของรูปหลายเหลี่ยมที่มีหน้าต่างการตัดจะพบจุดตัดหากขอบไม่สมบูรณ์ภายในหน้าต่างการตัดและขอบบางส่วนจากจุดตัดไปยังขอบด้านนอกจะถูกตัดออก รูปต่อไปนี้แสดงคลิปขอบซ้ายขวาบนและล่าง -
การตัดข้อความ
มีการใช้เทคนิคต่างๆในการตัดข้อความในคอมพิวเตอร์กราฟิก ขึ้นอยู่กับวิธีการที่ใช้ในการสร้างตัวละครและข้อกำหนดของแอปพลิเคชันเฉพาะ มีสามวิธีในการตัดข้อความตามรายการด้านล่าง -
- การตัดสตริงทั้งหมดหรือไม่มีเลย
- การตัดอักขระทั้งหมดหรือไม่มีเลย
- การตัดข้อความ
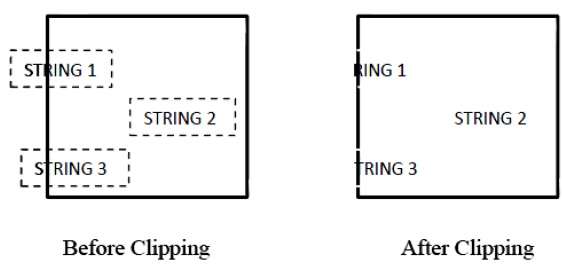
รูปต่อไปนี้แสดงการตัดสตริงทั้งหมดหรือไม่มีเลย -
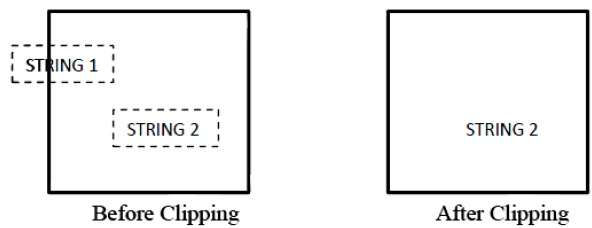
ในวิธีการตัดสตริงทั้งหมดหรือไม่มีเลยเราจะเก็บสตริงทั้งหมดไว้หรือเราปฏิเสธสตริงทั้งหมดตามหน้าต่างการตัด ดังที่แสดงในรูปด้านบน STRING2 จะอยู่ภายในหน้าต่างการตัดดังนั้นเราจึงเก็บไว้และ STRING1 อยู่ในหน้าต่างเพียงบางส่วนเท่านั้นเราจึงปฏิเสธ
รูปต่อไปนี้แสดงการตัดอักขระทั้งหมดหรือไม่มีเลย -
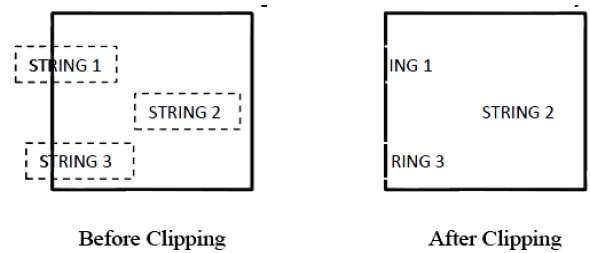
วิธีการตัดนี้ขึ้นอยู่กับอักขระแทนที่จะเป็นสตริงทั้งหมด ในวิธีนี้หากสตริงอยู่ในหน้าต่างการตัดต่อทั้งหมดเราจะเก็บไว้ หากอยู่นอกหน้าต่างบางส่วน -
คุณปฏิเสธเฉพาะส่วนของสตริงที่อยู่ภายนอก
หากอักขระอยู่บนขอบเขตของหน้าต่างคลิปเราจะทิ้งอักขระนั้นทั้งหมดและเก็บสตริงส่วนที่เหลือไว้
รูปต่อไปนี้แสดงการตัดข้อความ -
วิธีการตัดนี้ขึ้นอยู่กับอักขระแทนที่จะเป็นสตริงทั้งหมด ในวิธีนี้หากสตริงอยู่ในหน้าต่างการตัดต่อทั้งหมดเราจะเก็บไว้ หากอยู่นอกหน้าต่างบางส่วน
คุณปฏิเสธเฉพาะส่วนของสตริงที่อยู่ภายนอก
หากอักขระอยู่ในขอบเขตของหน้าต่างการคลิปเราจะทิ้งเฉพาะส่วนของอักขระที่อยู่นอกหน้าต่างการตัด
กราฟิกบิตแมป
บิตแมปคือชุดของพิกเซลที่อธิบายรูปภาพ เป็นคอมพิวเตอร์กราฟิกประเภทหนึ่งที่คอมพิวเตอร์ใช้ในการจัดเก็บและแสดงรูปภาพ ในกราฟิกประเภทนี้รูปภาพจะถูกจัดเก็บทีละนิดดังนั้นจึงมีชื่อว่ากราฟิก Bit-map เพื่อความเข้าใจที่ดีขึ้นให้เราพิจารณาตัวอย่างต่อไปนี้ที่เราวาดหน้ายิ้มโดยใช้กราฟิกบิตแมป

ตอนนี้เราจะมาดูกันว่าใบหน้าที่ยิ้มนี้ถูกจัดเก็บทีละนิดในคอมพิวเตอร์กราฟิกอย่างไร
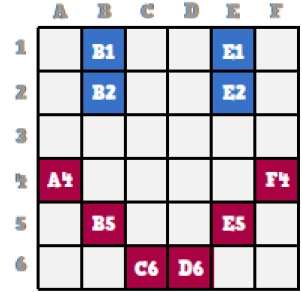
จากการสังเกตใบหน้าสไมลี่ดั้งเดิมอย่างใกล้ชิดเราจะเห็นว่ามีเส้นสีน้ำเงินสองเส้นซึ่งแสดงเป็น B1, B2 และ E1, E2 ในรูปด้านบน
ในทำนองเดียวกันสไมลี่จะแสดงโดยใช้บิตผสมของ A4, B5, C6, D6, E5 และ F4 ตามลำดับ
ข้อเสียเปรียบหลักของกราฟิกบิตแมปคือ -
เราไม่สามารถปรับขนาดภาพบิตแมปได้ หากคุณพยายามปรับขนาดพิกเซลจะเบลอ
บิตแมปสีอาจมีขนาดใหญ่มาก
การเปลี่ยนแปลงหมายถึงการเปลี่ยนกราฟิกบางส่วนให้เป็นอย่างอื่นโดยใช้กฎ เราสามารถเปลี่ยนรูปแบบได้หลายแบบเช่นการแปลการปรับขนาดขึ้นหรือลงการหมุนการตัดเฉือน ฯลฯ เมื่อการเปลี่ยนแปลงเกิดขึ้นบนระนาบ 2 มิติจะเรียกว่าการแปลง 2 มิติ
การแปลงร่างมีบทบาทสำคัญในคอมพิวเตอร์กราฟิกเพื่อจัดตำแหน่งกราฟิกบนหน้าจอและเปลี่ยนขนาดหรือการวางแนว
พิกัดที่เป็นเนื้อเดียวกัน
ในการดำเนินการตามลำดับของการเปลี่ยนแปลงเช่นการแปลตามด้วยการหมุนและการปรับขนาดเราจำเป็นต้องทำตามกระบวนการตามลำดับ -
- แปลพิกัด
- หมุนพิกัดที่แปลแล้วจากนั้น
- ปรับขนาดพิกัดที่หมุนเพื่อทำการแปลงคอมโพสิตให้เสร็จสมบูรณ์
เพื่อให้กระบวนการนี้สั้นลงเราต้องใช้เมทริกซ์การแปลง 3 × 3 แทนเมทริกซ์การแปลง 2 × 2 ในการแปลงเมทริกซ์ 2 × 2 เป็นเมทริกซ์ 3 × 3 เราต้องเพิ่มพิกัดดัมมี่พิเศษ W
ด้วยวิธีนี้เราสามารถแทนจุดด้วยตัวเลข 3 ตัวแทนที่จะเป็น 2 จำนวนซึ่งเรียกว่า Homogenous Coordinateระบบ. ในระบบนี้เราสามารถแสดงสมการการแปลงทั้งหมดในการคูณเมทริกซ์ จุดคาร์ทีเซียน P (X, Y) สามารถแปลงเป็นพิกัดที่เป็นเนื้อเดียวกันได้โดย P '(X h , Y h , h)
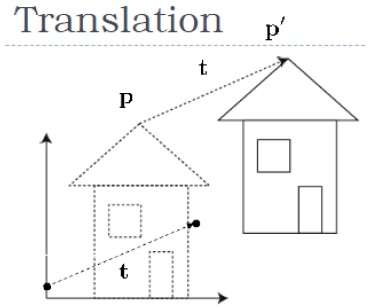
การแปล
การแปลจะย้ายวัตถุไปยังตำแหน่งอื่นบนหน้าจอ คุณสามารถแปลจุดใน 2 มิติได้โดยเพิ่มพิกัดการแปล (t x , t y ) ไปยังพิกัดเดิม (X, Y) เพื่อรับพิกัดใหม่ (X ', Y')
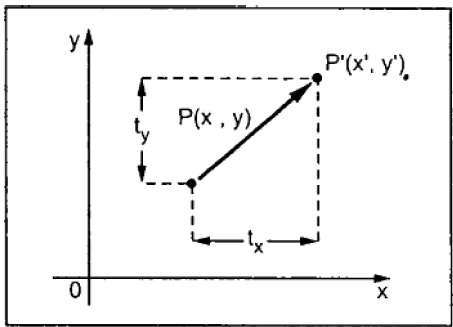
จากรูปด้านบนคุณสามารถเขียนได้ว่า -
X’ = X + tx
Y’ = Y + ty
คู่ (t x , t y ) เรียกว่าเวกเตอร์การแปลหรือกะเวกเตอร์ สมการข้างต้นสามารถแสดงโดยใช้เวกเตอร์คอลัมน์
$P = \frac{[X]}{[Y]}$ p '= $\frac{[X']}{[Y']}$T = $\frac{[t_{x}]}{[t_{y}]}$
เราสามารถเขียนเป็น -
P’ = P + T
การหมุน
ในการหมุนเราหมุนวัตถุที่มุมเฉพาะθ (theta) จากจุดกำเนิด จากรูปต่อไปนี้เราจะเห็นว่าจุด P (X, Y) อยู่ที่มุมφจากพิกัด X แนวนอนโดยมีระยะทาง r จากจุดกำเนิด
สมมติว่าคุณต้องการหมุนที่มุมθ หลังจากหมุนไปยังตำแหน่งใหม่คุณจะได้รับจุดใหม่ P '(X', Y ')

การใช้ตรีโกณมิติมาตรฐานพิกัดดั้งเดิมของจุด P (X, Y) สามารถแสดงเป็น -
$X = r \, cos \, \phi ...... (1)$
$Y = r \, sin \, \phi ...... (2)$
เช่นเดียวกับที่เราสามารถแทนจุด P '(X', Y ') เป็น -
${x}'= r \: cos \: \left ( \phi \: + \: \theta \right ) = r\: cos \: \phi \: cos \: \theta \: − \: r \: sin \: \phi \: sin \: \theta ....... (3)$
${y}'= r \: sin \: \left ( \phi \: + \: \theta \right ) = r\: cos \: \phi \: sin \: \theta \: + \: r \: sin \: \phi \: cos \: \theta ....... (4)$
การแทนสมการ (1) & (2) ใน (3) & (4) ตามลำดับเราจะได้
${x}'= x \: cos \: \theta − \: y \: sin \: \theta $
${y}'= x \: sin \: \theta + \: y \: cos \: \theta $
แทนสมการข้างต้นในรูปแบบเมทริกซ์
$$[X' Y'] = [X Y] \begin{bmatrix} cos\theta & sin\theta \\ −sin\theta & cos\theta \end{bmatrix}OR $$
P '= P ∙ R
โดยที่ R คือเมทริกซ์การหมุน
$$R = \begin{bmatrix} cos\theta & sin\theta \\ −sin\theta & cos\theta \end{bmatrix}$$
มุมการหมุนสามารถเป็นบวกและลบได้
สำหรับมุมการหมุนที่เป็นบวกเราสามารถใช้เมทริกซ์การหมุนด้านบนได้ อย่างไรก็ตามสำหรับการหมุนมุมลบเมทริกซ์จะเปลี่ยนไปตามที่แสดงด้านล่าง -
$$R = \begin{bmatrix} cos(−\theta) & sin(−\theta) \\ -sin(−\theta) & cos(−\theta) \end{bmatrix}$$
$$=\begin{bmatrix} cos\theta & −sin\theta \\ sin\theta & cos\theta \end{bmatrix} \left (\because cos(−\theta ) = cos \theta \; and\; sin(−\theta ) = −sin \theta \right )$$
การปรับขนาด
ในการเปลี่ยนขนาดของวัตถุจะใช้การแปลงมาตราส่วน ในกระบวนการปรับขนาดคุณสามารถขยายหรือบีบอัดขนาดของวัตถุได้ การปรับมาตราส่วนสามารถทำได้โดยการคูณพิกัดเดิมของวัตถุด้วยตัวคูณมาตราส่วนเพื่อให้ได้ผลลัพธ์ที่ต้องการ
ให้เราสมมติว่าพิกัดเดิมคือ (X, Y) ปัจจัยการปรับขนาดคือ (S X , S Y ) และพิกัดที่ผลิตคือ (X ', Y') สิ่งนี้สามารถแสดงทางคณิตศาสตร์ได้ดังที่แสดงด้านล่าง -
X' = X . SX and Y' = Y . SY
ปัจจัยการปรับขนาด S X , S Y จะปรับขนาดวัตถุในทิศทาง X และ Y ตามลำดับ สมการข้างต้นสามารถแสดงในรูปแบบเมทริกซ์ดังต่อไปนี้ -
$$\binom{X'}{Y'} = \binom{X}{Y} \begin{bmatrix} S_{x} & 0\\ 0 & S_{y} \end{bmatrix}$$
หรือ
P’ = P . S
โดยที่ S คือเมทริกซ์มาตราส่วน ขั้นตอนการปรับขนาดจะแสดงในรูปต่อไปนี้
ถ้าเราให้ค่าน้อยกว่า 1 ให้กับค่ามาตราส่วน S เราก็สามารถลดขนาดของวัตถุได้ หากเราให้ค่ามากกว่า 1 เราก็สามารถเพิ่มขนาดของวัตถุได้
การสะท้อนกลับ
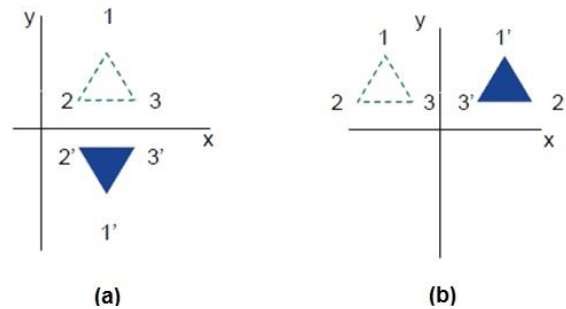
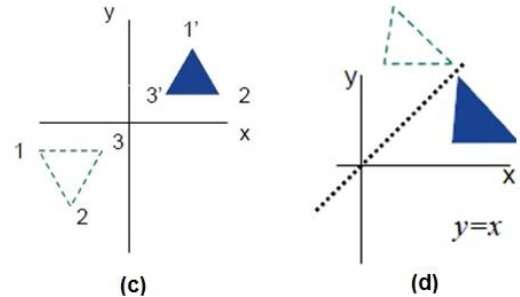
การสะท้อนกลับคือภาพสะท้อนของวัตถุดั้งเดิม กล่าวอีกนัยหนึ่งเราสามารถพูดได้ว่าเป็นการหมุน 180 ° ในการเปลี่ยนแปลงการสะท้อนขนาดของวัตถุจะไม่เปลี่ยนแปลง
ตัวเลขต่อไปนี้แสดงการสะท้อนตามแกน X และ Y และเกี่ยวกับจุดกำเนิดตามลำดับ
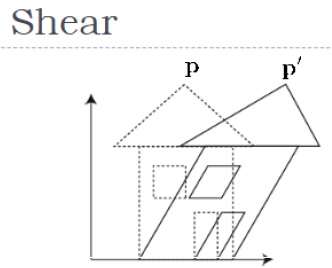
เฉือน
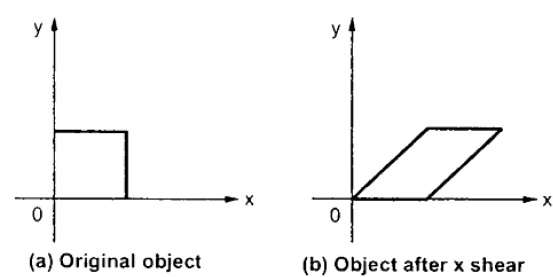
การเปลี่ยนแปลงที่เอียงรูปร่างของวัตถุเรียกว่าการแปลงเฉือน มีการแปลงเฉือนสองแบบX-Shear และ Y-Shear. หนึ่งกะค่าพิกัด X และค่าพิกัด Y กะอื่น ๆ อย่างไรก็ตาม; ในทั้งสองกรณีมีเพียงพิกัดเดียวเท่านั้นที่เปลี่ยนพิกัดและอื่น ๆ จะรักษาค่าไว้ การตัดเฉือนเรียกอีกอย่างว่าSkewing.
X-Shear
X-Shear จะรักษาพิกัด Y และทำการเปลี่ยนแปลงพิกัด X ซึ่งทำให้เส้นแนวตั้งเอียงไปทางขวาหรือซ้ายดังแสดงในรูปด้านล่าง
เมทริกซ์การเปลี่ยนแปลงสำหรับ X-Shear สามารถแสดงเป็น -
$$X_{sh} = \begin{bmatrix} 1& shx& 0\\ 0& 1& 0\\ 0& 0& 1 \end{bmatrix}$$
Y '= Y + Sh y . X
X '= X
Y- เฉือน
Y-Shear รักษาพิกัด X และเปลี่ยนพิกัด Y ซึ่งทำให้เส้นแนวนอนเปลี่ยนเป็นเส้นที่ลาดขึ้นหรือลงดังแสดงในรูปต่อไปนี้
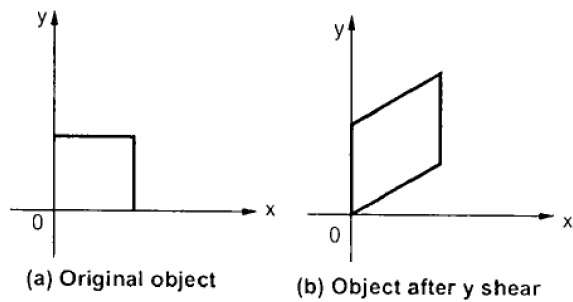
Y-Shear สามารถแสดงในเมทริกซ์จาก -
$$Y_{sh} \begin{bmatrix} 1& 0& 0\\ shy& 1& 0\\ 0& 0& 1 \end{bmatrix}$$
X'= X + Sh x ย
Y '= Y
การแปลงคอมโพสิต
หากการแปลงระนาบ T1 ตามด้วยการแปลงระนาบที่สอง T2 ผลลัพธ์อาจถูกแทนด้วยการแปลงครั้งเดียว T ซึ่งเป็นองค์ประกอบของ T1 และ T2 ตามลำดับนั้น สิ่งนี้เขียนเป็น T = T1 ∙ T2
การแปลงคอมโพสิตสามารถทำได้โดยการต่อเมทริกซ์การแปลงเพื่อให้ได้เมทริกซ์การแปลงแบบรวม
เมทริกซ์รวม -
[T][X] = [X] [T1] [T2] [T3] [T4] …. [Tn]
โดยที่ [Ti] คือการรวมกันของ
- Translation
- Scaling
- Shearing
- Rotation
- Reflection
การเปลี่ยนแปลงลำดับของการแปลงจะนำไปสู่ผลลัพธ์ที่แตกต่างกันเนื่องจากโดยทั่วไปการคูณเมทริกซ์ไม่ใช่การสะสมนั่นคือ [A] [B] ≠ [B]. [A] และลำดับของการคูณ จุดประสงค์พื้นฐานของการสร้างการเปลี่ยนแปลงคือการเพิ่มประสิทธิภาพโดยใช้การแปลงแบบประกอบเพียงครั้งเดียวไปยังจุดหนึ่งแทนที่จะใช้ชุดของการเปลี่ยนแปลงทีละอย่าง
ตัวอย่างเช่นในการหมุนวัตถุเกี่ยวกับจุดใดจุดหนึ่ง (X p , Y p ) เราต้องดำเนินการสามขั้นตอน -
- แปลจุด (X p , Y p ) เป็นจุดเริ่มต้น
- หมุนมันเกี่ยวกับจุดกำเนิด
- สุดท้ายให้แปลจุดศูนย์กลางของการหมุนกลับที่เดิม
ในระบบ 2D เราใช้เพียงสองพิกัด X และ Y แต่ใน 3 มิติจะมีการเพิ่มพิกัด Z เพิ่มเติม เทคนิคกราฟิก 3 มิติและการประยุกต์ใช้เป็นพื้นฐานในอุตสาหกรรมบันเทิงเกมและคอมพิวเตอร์ช่วยออกแบบ เป็นพื้นที่ต่อเนื่องของการวิจัยในการสร้างภาพทางวิทยาศาสตร์
นอกจากนี้ส่วนประกอบกราฟิก 3 มิติยังเป็นส่วนหนึ่งของคอมพิวเตอร์ส่วนบุคคลเกือบทุกเครื่องและแม้ว่าโดยปกติแล้วจะมีไว้สำหรับซอฟต์แวร์ที่เน้นกราฟิกเช่นเกม แต่แอปพลิเคชันอื่น ๆ
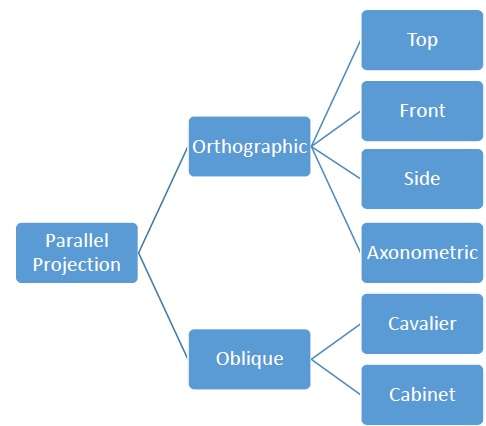
การฉายภาพคู่ขนาน
การฉายภาพแบบขนานจะทิ้งพิกัด z และเส้นขนานจากจุดยอดแต่ละจุดบนวัตถุจะขยายออกไปจนกว่าจะตัดกับระนาบมุมมอง ในการฉายภาพคู่ขนานเราระบุทิศทางของการฉายภาพแทนที่จะเป็นจุดศูนย์กลางของการฉายภาพ
ในการฉายแบบขนานระยะห่างจากจุดศูนย์กลางของการฉายถึงระนาบโครงการจะไม่มีที่สิ้นสุด ในการฉายภาพประเภทนี้เราเชื่อมต่อจุดยอดที่คาดการณ์ไว้ตามส่วนของเส้นซึ่งสอดคล้องกับการเชื่อมต่อบนวัตถุดั้งเดิม
การฉายภาพคู่ขนานมีความสมจริงน้อยกว่า แต่เหมาะสำหรับการวัดที่แน่นอน ในการคาดคะเนประเภทนี้เส้นขนานจะยังคงขนานกันและไม่คงมุมไว้ การคาดการณ์แบบขนานประเภทต่างๆจะแสดงตามลำดับชั้นต่อไปนี้
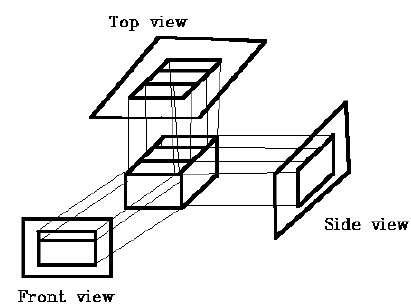
การฉายภาพ Orthographic
ในการฉายภาพออร์โทกราฟิคทิศทางของการฉายภาพเป็นเรื่องปกติสำหรับการฉายภาพของเครื่องบิน การคาดการณ์ออร์โธกราฟิกมีสามประเภท -
- การฉายภาพด้านหน้า
- การฉายภาพยอดนิยม
- การฉายภาพด้านข้าง
การฉายภาพเฉียง
ในการฉายภาพแนวเฉียงทิศทางของการฉายภาพไม่ปกติสำหรับการฉายภาพของระนาบ ในการฉายภาพแบบเฉียงเราสามารถดูวัตถุได้ดีกว่าการฉายภาพแบบออร์โทกราฟิค
การคาดการณ์แบบเฉียงมีสองประเภท - Cavalier และ Cabinet. การฉายภาพของ Cavalier ทำมุม 45 °ด้วยระนาบการฉายภาพ การฉายภาพของเส้นที่ตั้งฉากกับระนาบมุมมองมีความยาวเท่ากับเส้นในการฉายภาพของ Cavalier ในการฉายภาพของทหารม้าปัจจัยที่คาดการณ์ล่วงหน้าสำหรับทิศทางหลักทั้งสามจะเท่ากัน
การฉายภาพของคณะรัฐมนตรีทำมุม 63.4 °ด้วยระนาบการฉายภาพ ในการฉายภาพของตู้เส้นที่ตั้งฉากกับพื้นผิวการมองจะถูกคาดการณ์ไว้ที่ความยาวจริง การคาดการณ์ทั้งสองจะแสดงในรูปต่อไปนี้ -

การคาดการณ์ภาพสามมิติ
เรียกว่าการคาดการณ์ออร์โธกราฟิกที่แสดงวัตถุมากกว่าหนึ่งด้าน axonometric orthographic projections. การฉายภาพแอกโซโนเมตริกที่พบบ่อยที่สุดคือไฟล์isometric projectionโดยที่ระนาบการฉายตัดกับแกนพิกัดแต่ละแกนในระบบพิกัดของโมเดลในระยะทางที่เท่ากัน ในการฉายภาพความขนานของเส้นจะถูกรักษาไว้ แต่มุมจะไม่ถูกเก็บรักษาไว้ รูปต่อไปนี้แสดงการฉายภาพสามมิติ -

การฉายภาพมุมมอง
ในการฉายแบบมุมมองระยะห่างจากจุดศูนย์กลางของการฉายไปยังระนาบโครงการนั้นมี จำกัด และขนาดของวัตถุจะแปรผกผันตามระยะทางซึ่งดูสมจริงกว่า
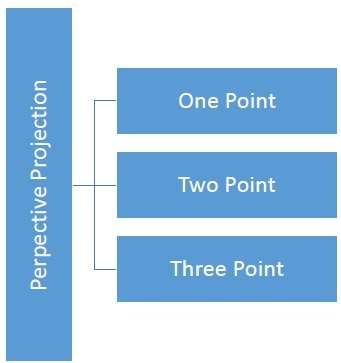
ระยะห่างและมุมจะไม่ถูกรักษาและเส้นขนานจะไม่ขนานกัน แต่พวกเขาทั้งหมดมาบรรจบกันที่จุดเดียวที่เรียกว่าcenter of projection หรือ projection reference point. การคาดการณ์มุมมองมี 3 ประเภทซึ่งแสดงในแผนภูมิต่อไปนี้
One point การฉายภาพเป็นเรื่องง่ายที่จะวาด
Two point การฉายภาพมุมมองให้การแสดงผลเชิงลึกที่ดีขึ้น
Three point การฉายภาพมุมมองเป็นเรื่องยากที่สุดในการวาด
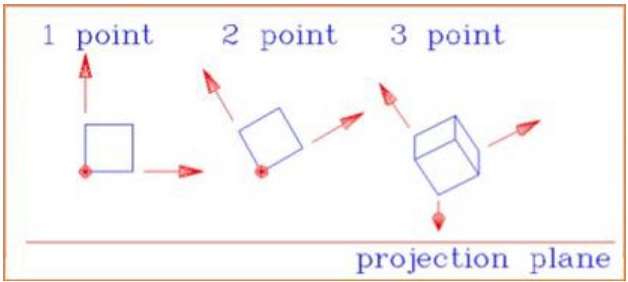
รูปต่อไปนี้แสดงการฉายมุมมองทั้งสามประเภท -
การแปล
ในการแปล 3 มิติเราถ่ายโอนพิกัด Z พร้อมกับพิกัด X และ Y กระบวนการแปลในรูปแบบ 3 มิติคล้ายกับการแปล 2 มิติ การแปลจะย้ายวัตถุไปยังตำแหน่งอื่นบนหน้าจอ
รูปต่อไปนี้แสดงผลของการแปล -
จุดสามารถแปลเป็น 3 มิติได้โดยการเพิ่มพิกัดการแปล $(t_{x,} t_{y,} t_{z})$ ไปยังพิกัดเดิม (X, Y, Z) เพื่อรับพิกัดใหม่ (X ', Y', Z ')
$T = \begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ t_{x}& t_{y}& t_{z}& 1\\ \end{bmatrix}$
P '= P ∙ T
$[X′ \:\: Y′ \:\: Z′ \:\: 1] \: = \: [X \:\: Y \:\: Z \:\: 1] \: \begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ t_{x}& t_{y}& t_{z}& 1\\ \end{bmatrix}$
$= [X + t_{x} \:\:\: Y + t_{y} \:\:\: Z + t_{z} \:\:\: 1]$
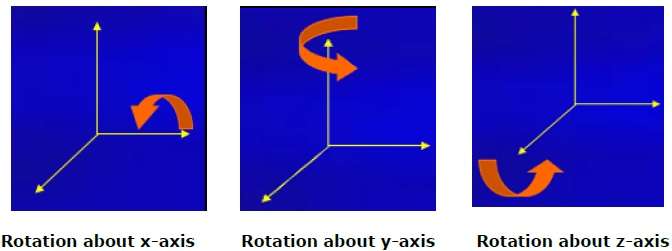
การหมุน
การหมุน 3 มิติไม่เหมือนกับการหมุน 2 มิติ ในการหมุน 3 มิติเราต้องระบุมุมของการหมุนพร้อมกับแกนของการหมุน เราสามารถทำการหมุน 3 มิติเกี่ยวกับแกน X, Y และ Z แสดงในรูปแบบเมทริกซ์ดังต่อไปนี้ -
$$R_{x}(\theta) = \begin{bmatrix} 1& 0& 0& 0\\ 0& cos\theta & −sin\theta& 0\\ 0& sin\theta & cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix} R_{y}(\theta) = \begin{bmatrix} cos\theta& 0& sin\theta& 0\\ 0& 1& 0& 0\\ −sin\theta& 0& cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix} R_{z}(\theta) =\begin{bmatrix} cos\theta & −sin\theta & 0& 0\\ sin\theta & cos\theta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1 \end{bmatrix}$$
รูปต่อไปนี้อธิบายการหมุนเกี่ยวกับแกนต่างๆ -
การปรับขนาด
คุณสามารถเปลี่ยนขนาดของวัตถุโดยใช้การแปลงมาตราส่วน ในกระบวนการปรับขนาดคุณสามารถขยายหรือบีบอัดขนาดของวัตถุได้ การปรับมาตราส่วนสามารถทำได้โดยการคูณพิกัดเดิมของวัตถุด้วยตัวคูณมาตราส่วนเพื่อให้ได้ผลลัพธ์ที่ต้องการ รูปต่อไปนี้แสดงผลของการปรับขนาด 3D -
ในการดำเนินการปรับมาตราส่วน 3 มิติจะใช้พิกัดสามพิกัด ให้เราสมมติว่าพิกัดเดิมคือ (X, Y, Z) ปัจจัยการปรับขนาดคือ$(S_{X,} S_{Y,} S_{z})$ตามลำดับและพิกัดที่ผลิตคือ (X ', Y', Z ') สิ่งนี้สามารถแสดงทางคณิตศาสตร์ได้ดังที่แสดงด้านล่าง -
$S = \begin{bmatrix} S_{x}& 0& 0& 0\\ 0& S_{y}& 0& 0\\ 0& 0& S_{z}& 0\\ 0& 0& 0& 1 \end{bmatrix}$
P '= P ∙ S
$[{X}' \:\:\: {Y}' \:\:\: {Z}' \:\:\: 1] = [X \:\:\:Y \:\:\: Z \:\:\: 1] \:\: \begin{bmatrix} S_{x}& 0& 0& 0\\ 0& S_{y}& 0& 0\\ 0& 0& S_{z}& 0\\ 0& 0& 0& 1 \end{bmatrix}$
$ = [X.S_{x} \:\:\: Y.S_{y} \:\:\: Z.S_{z} \:\:\: 1]$
เฉือน
การแปลงที่เอียงรูปร่างของวัตถุเรียกว่า shear transformation. เช่นเดียวกับการเฉือนแบบ 2 มิติเราสามารถเฉือนวัตถุตามแกน X แกน Y หรือแกน Z ในแบบ 3 มิติได้
ดังที่แสดงในรูปด้านบนมีพิกัด P คุณสามารถเฉือนมันเพื่อให้ได้พิกัด P 'ใหม่ซึ่งสามารถแสดงในรูปแบบเมทริกซ์ 3 มิติดังต่อไปนี้ -
$Sh = \begin{bmatrix} 1 & sh_{x}^{y} & sh_{x}^{z} & 0 \\ sh_{y}^{x} & 1 & sh_{y}^{z} & 0 \\ sh_{z}^{x} & sh_{z}^{y} & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$
P '= P ∙ช
$X’ = X + Sh_{x}^{y} Y + Sh_{x}^{z} Z$
$Y' = Sh_{y}^{x}X + Y +sh_{y}^{z}Z$
$Z' = Sh_{z}^{x}X + Sh_{z}^{y}Y + Z$
เมทริกซ์การเปลี่ยนแปลง
เมทริกซ์การแปลงร่างเป็นเครื่องมือพื้นฐานสำหรับการเปลี่ยนแปลง เมทริกซ์ที่มีขนาด nxm ถูกคูณด้วยพิกัดของวัตถุ โดยปกติเมทริกซ์ 3 x 3 หรือ 4 x 4 จะใช้สำหรับการแปลง ตัวอย่างเช่นพิจารณาเมทริกซ์ต่อไปนี้สำหรับการดำเนินการต่างๆ
| $T = \begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ t_{x}& t_{y}& t_{z}& 1\\ \end{bmatrix}$ | $S = \begin{bmatrix} S_{x}& 0& 0& 0\\ 0& S_{y}& 0& 0\\ 0& 0& S_{z}& 0\\ 0& 0& 0& 1 \end{bmatrix}$ | $Sh = \begin{bmatrix} 1& sh_{x}^{y}& sh_{x}^{z}& 0\\ sh_{y}^{x}& 1 & sh_{y}^{z}& 0\\ sh_{z}^{x}& sh_{z}^{y}& 1& 0\\ 0& 0& 0& 1 \end{bmatrix}$ |
| Translation Matrix | Scaling Matrix | Shear Matrix |
| $R_{x}(\theta) = \begin{bmatrix} 1& 0& 0& 0\\ 0& cos\theta & -sin\theta& 0\\ 0& sin\theta & cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix}$ | $R_{y}(\theta) = \begin{bmatrix} cos\theta& 0& sin\theta& 0\\ 0& 1& 0& 0\\ -sin\theta& 0& cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix}$ | $R_{z}(\theta) = \begin{bmatrix} cos\theta & -sin\theta & 0& 0\\ sin\theta & cos\theta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1 \end{bmatrix}$ |
| Rotation Matrix | ||
ในคอมพิวเตอร์กราฟิกเรามักจะต้องวาดวัตถุประเภทต่างๆลงบนหน้าจอ วัตถุไม่ได้แบนตลอดเวลาและเราต้องวาดเส้นโค้งหลาย ๆ ครั้งเพื่อวาดวัตถุ
ประเภทของเส้นโค้ง
เส้นโค้งคือชุดของจุดที่มีขนาดใหญ่ไม่สิ้นสุด แต่ละจุดมีเพื่อนบ้านสองจุดยกเว้นจุดสิ้นสุด เส้นโค้งสามารถแบ่งออกเป็นสามประเภทอย่างกว้าง ๆ -explicit, implicit, และ parametric curves.
เส้นโค้งโดยปริยาย
การแสดงเส้นโค้งโดยปริยายกำหนดชุดของจุดบนเส้นโค้งโดยใช้ขั้นตอนที่สามารถทดสอบเพื่อดูว่ามีจุดบนเส้นโค้งหรือไม่ โดยปกติแล้วเส้นโค้งโดยปริยายจะถูกกำหนดโดยฟังก์ชันโดยนัยของแบบฟอร์ม -
f (x, y) = 0
สามารถแสดงเส้นโค้งหลายค่า (ค่า y หลายค่าสำหรับค่า x) ตัวอย่างทั่วไปคือวงกลมซึ่งมีการแสดงโดยนัยคือ
x2 + y2 - R2 = 0
เส้นโค้งที่ชัดเจน
ฟังก์ชันทางคณิตศาสตร์ y = f (x) สามารถพล็อตเป็นเส้นโค้งได้ ฟังก์ชันดังกล่าวเป็นการแสดงเส้นโค้งอย่างชัดเจน การแสดงที่ชัดเจนไม่ได้เป็นแบบทั่วไปเนื่องจากไม่สามารถแสดงเส้นแนวตั้งและเป็นค่าเดียว สำหรับค่า x แต่ละค่าโดยปกติฟังก์ชันจะคำนวณค่า y เพียงค่าเดียวเท่านั้น
เส้นโค้งพาราเมตริก
เส้นโค้งที่มีรูปแบบพาราเมตริกเรียกว่าเส้นโค้งพาราเมตริก การแสดงเส้นโค้งโดยชัดแจ้งและโดยปริยายสามารถใช้ได้เฉพาะเมื่อทราบฟังก์ชันเท่านั้น ในทางปฏิบัติจะใช้เส้นโค้งพาราเมตริก เส้นโค้งพาราเมตริกสองมิติมีรูปแบบต่อไปนี้ -
P (t) = f (t), g (t) หรือ P (t) = x (t), y (t)
ฟังก์ชัน f และ g จะกลายเป็นพิกัด (x, y) ของจุดใด ๆ บนเส้นโค้งและจุดจะได้รับเมื่อพารามิเตอร์ t มีการเปลี่ยนแปลงในช่วงเวลาหนึ่ง [a, b] ตามปกติ [0, 1]
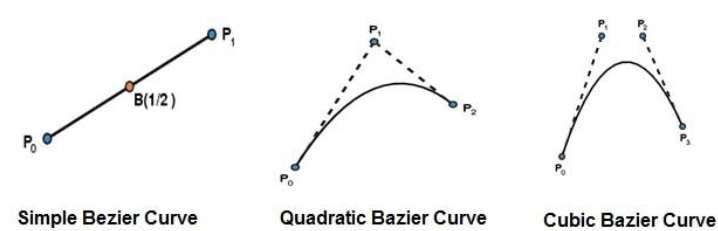
Bezier Curves
Bezier curve ถูกค้นพบโดยวิศวกรชาวฝรั่งเศส Pierre Bézier. เส้นโค้งเหล่านี้สามารถสร้างขึ้นได้ภายใต้การควบคุมของจุดอื่น ๆ เส้นสัมผัสโดยประมาณโดยใช้จุดควบคุมถูกใช้เพื่อสร้างเส้นโค้ง เส้นโค้ง Bezier สามารถแสดงทางคณิตศาสตร์เป็น -
$$\sum_{k=0}^{n} P_{i}{B_{i}^{n}}(t)$$
ที่ไหน $p_{i}$ คือชุดของคะแนนและ ${B_{i}^{n}}(t)$ แสดงถึงพหุนามเบิร์นสไตน์ซึ่งกำหนดโดย -
$${B_{i}^{n}}(t) = \binom{n}{i} (1 - t)^{n-i}t^{i}$$
ที่ไหน n คือระดับพหุนาม i คือดัชนีและ t คือตัวแปร
เส้นโค้งเบซิเอร์ที่ง่ายที่สุดคือเส้นตรงจากจุด $P_{0}$ ถึง $P_{1}$. เส้นโค้ง Bezier กำลังสองถูกกำหนดโดยจุดควบคุมสามจุด เส้นโค้ง Bezier ลูกบาศก์ถูกกำหนดโดยจุดควบคุมสี่จุด
คุณสมบัติของ Bezier Curves
เส้นโค้ง Bezier มีคุณสมบัติดังต่อไปนี้ -
โดยทั่วไปจะเป็นไปตามรูปร่างของรูปหลายเหลี่ยมควบคุมซึ่งประกอบด้วยส่วนที่เชื่อมต่อกับจุดควบคุม
พวกเขามักจะผ่านจุดควบคุมแรกและจุดสุดท้าย
มีอยู่ในตัวถังนูนของจุดควบคุมที่กำหนด
ระดับของพหุนามที่กำหนดส่วนโค้งจะน้อยกว่าจำนวนของการกำหนดจุดรูปหลายเหลี่ยม ดังนั้นสำหรับจุดควบคุม 4 จุดองศาของพหุนามคือ 3 คือพหุนามลูกบาศก์
โดยทั่วไปเส้นโค้ง Bezier จะเป็นไปตามรูปร่างของรูปหลายเหลี่ยมที่กำหนด
ทิศทางของเวกเตอร์แทนเจนต์ที่จุดสิ้นสุดจะเหมือนกับเวกเตอร์ที่กำหนดโดยส่วนแรกและส่วนสุดท้าย
คุณสมบัติตัวถังนูนสำหรับเส้นโค้ง Bezier ช่วยให้มั่นใจได้ว่าพหุนามเป็นไปตามจุดควบคุมอย่างราบรื่น
ไม่มีเส้นตรงตัดกับเส้นโค้งเบเซียร์มากกว่าที่จะตัดกับรูปหลายเหลี่ยมควบคุม
พวกมันไม่แปรผันภายใต้การเปลี่ยนแปลงของความสัมพันธ์
เส้นโค้งของ Bezier แสดงการควบคุมทั่วโลกหมายถึงการย้ายจุดควบคุมจะเปลี่ยนรูปร่างของเส้นโค้งทั้งหมด
เส้นโค้ง Bezier ที่ระบุสามารถแบ่งย่อยได้ที่จุด t = t0 เป็นสองส่วน Bezier ซึ่งรวมเข้าด้วยกันที่จุดที่สอดคล้องกับค่าพารามิเตอร์ t = t0
เส้นโค้ง B-Spline
เส้นโค้ง Bezier ที่ผลิตโดยฟังก์ชันพื้นฐานของ Bernstein มีความยืดหยุ่น จำกัด
ขั้นแรกจำนวนของจุดยอดรูปหลายเหลี่ยมที่ระบุจะแก้ไขลำดับของพหุนามที่เป็นผลลัพธ์ซึ่งกำหนดเส้นโค้ง
ลักษณะการ จำกัด ประการที่สองคือค่าของฟังก์ชันการผสมไม่เป็นศูนย์สำหรับค่าพารามิเตอร์ทั้งหมดในเส้นโค้งทั้งหมด
พื้นฐาน B-spline ประกอบด้วยพื้นฐาน Bernstein เป็นกรณีพิเศษ พื้นฐาน B-spline ไม่ใช่ทั่วโลก
เส้นโค้ง B-spline หมายถึงการรวมกันเชิงเส้นของจุดควบคุม Pi และฟังก์ชันพื้นฐาน B-spline $N_{i,}$ k (t) กำหนดโดย
$C(t) = \sum_{i=0}^{n}P_{i}N_{i,k}(t),$ $n\geq k-1,$ $t\: \epsilon \: [ tk-1,tn+1 ]$
ที่ไหน
{$p_{i}$: i = 0, 1, 2 … .n} เป็นจุดควบคุม
k คือลำดับของส่วนพหุนามของเส้นโค้ง B-spline ลำดับ k หมายความว่าเส้นโค้งประกอบด้วยส่วนพหุนามแบบทีละส่วนขององศา k - 1
ที่ $N_{i,k}(t)$คือ“ ฟังก์ชันการผสม B-spline แบบปกติ” พวกเขาอธิบายโดยลำดับ k และโดยลำดับที่ไม่ลดลงของจำนวนจริงโดยปกติเรียกว่า "ลำดับปม"
$${t_{i}:i = 0, ... n + K}$$
ฟังก์ชัน N i , k อธิบายไว้ดังนี้ -
$$N_{i,1}(t) = \left\{\begin{matrix} 1,& if \:u \: \epsilon \: [t_{i,}t_{i+1}) \\ 0,& Otherwise \end{matrix}\right.$$
และถ้า k> 1
$$N_{i,k}(t) = \frac{t-t_{i}}{t_{i+k-1}} N_{i,k-1}(t) + \frac{t_{i+k}-t}{t_{i+k} - t_{i+1}} N_{i+1,k-1}(t)$$
และ
$$t \: \epsilon \: [t_{k-1},t_{n+1})$$
คุณสมบัติของ B-spline Curve
เส้นโค้ง B-spline มีคุณสมบัติดังต่อไปนี้ -
ผลรวมของฟังก์ชันพื้นฐาน B-spline สำหรับค่าพารามิเตอร์คือ 1
ฟังก์ชันพื้นฐานแต่ละฟังก์ชันเป็นบวกหรือศูนย์สำหรับค่าพารามิเตอร์ทั้งหมด
แต่ละฟังก์ชันพื้นฐานมีค่าสูงสุดหนึ่งค่าอย่างแม่นยำยกเว้น k = 1
ลำดับสูงสุดของเส้นโค้งเท่ากับจำนวนจุดยอดของการกำหนดรูปหลายเหลี่ยม
ระดับของพหุนาม B-spline นั้นไม่ขึ้นกับจำนวนจุดยอดของการกำหนดรูปหลายเหลี่ยม
B-spline ช่วยให้สามารถควบคุมพื้นผิวเส้นโค้งได้เนื่องจากจุดยอดแต่ละจุดมีผลต่อรูปร่างของเส้นโค้งในช่วงของค่าพารามิเตอร์เท่านั้นที่ฟังก์ชันพื้นฐานที่เกี่ยวข้องไม่เป็นศูนย์
เส้นโค้งแสดงคุณสมบัติที่ลดน้อยลงของรูปแบบ
เส้นโค้งโดยทั่วไปเป็นไปตามรูปร่างของการกำหนดรูปหลายเหลี่ยม
การแปลงความสัมพันธ์ใด ๆ สามารถนำไปใช้กับเส้นโค้งได้โดยนำไปใช้กับจุดยอดของการกำหนดรูปหลายเหลี่ยม
เส้นโค้งภายในตัวถังนูนของรูปหลายเหลี่ยมที่กำหนด
พื้นผิวรูปหลายเหลี่ยม
วัตถุถูกแสดงเป็นชุดของพื้นผิว การแสดงวัตถุ 3 มิติแบ่งออกเป็นสองประเภท
Boundary Representations (B-reps) - อธิบายวัตถุ 3 มิติว่าเป็นชุดของพื้นผิวที่แยกการตกแต่งภายในของวัตถุออกจากสภาพแวดล้อม
Space–partitioning representations - ใช้เพื่ออธิบายคุณสมบัติภายในโดยการแบ่งพื้นที่เชิงพื้นที่ที่มีวัตถุเป็นชุดของแข็งขนาดเล็กที่ไม่ทับซ้อนกัน (โดยปกติจะเป็นลูกบาศก์)
การแสดงขอบเขตที่ใช้บ่อยที่สุดสำหรับวัตถุกราฟิก 3 มิติคือชุดของรูปหลายเหลี่ยมพื้นผิวที่ล้อมรอบภายในวัตถุ ระบบกราฟิกจำนวนมากใช้วิธีนี้ ชุดรูปหลายเหลี่ยมถูกเก็บไว้สำหรับคำอธิบายวัตถุ สิ่งนี้ช่วยลดความซับซ้อนและเพิ่มความเร็วในการแสดงพื้นผิวและการแสดงวัตถุเนื่องจากพื้นผิวทั้งหมดสามารถอธิบายได้ด้วยสมการเชิงเส้น
พื้นผิวรูปหลายเหลี่ยมเป็นเรื่องปกติในการออกแบบและการสร้างแบบจำลองของแข็งเนื่องจาก wireframe displayสามารถทำได้อย่างรวดเร็วเพื่อแสดงโครงสร้างพื้นผิวโดยทั่วไป จากนั้นฉากที่สมจริงจะถูกสร้างขึ้นโดยการสอดแทรกรูปแบบการแรเงาบนพื้นผิวรูปหลายเหลี่ยมเพื่อให้แสงสว่าง
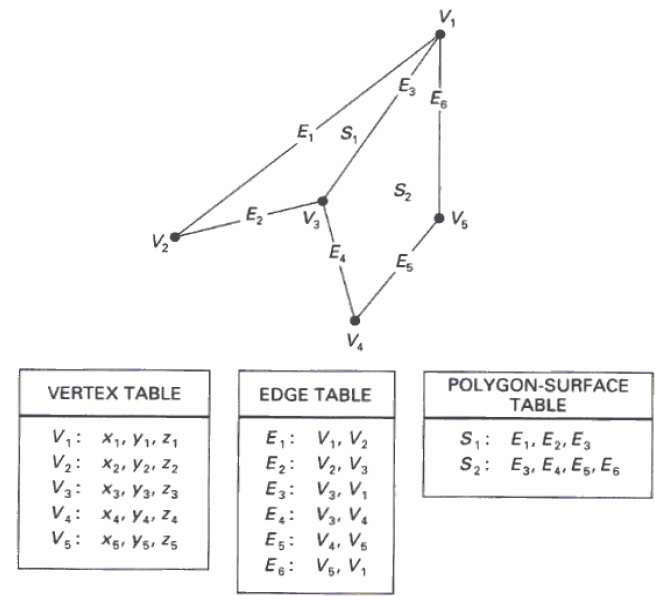
ตารางรูปหลายเหลี่ยม
ในวิธีนี้พื้นผิวจะถูกระบุโดยชุดพิกัดจุดยอดและแอตทริบิวต์ที่เกี่ยวข้อง ดังแสดงในรูปต่อไปนี้มีห้าจุดจาก v 1ไปทาง v 5
ร้านค้ายอดแต่ละ x, y, z และข้อมูลพิกัดซึ่งเป็นตัวแทนในตารางเป็นโวลต์1 : x 1 , y 1 , Z 1
ตาราง Edge ใช้เพื่อเก็บข้อมูลขอบของรูปหลายเหลี่ยม ในรูปต่อไปขอบ E 1อยู่ระหว่างจุดสุดยอดวี1และวี2ซึ่งเป็นตัวแทนในตารางเป็น E 1 : โวลต์1โวลต์2
ตารางพื้นผิวรูปหลายเหลี่ยมเก็บจำนวนพื้นผิวที่มีอยู่ในรูปหลายเหลี่ยม จากตัวเลขดังต่อไปนี้พื้นผิว S 1ถูกปกคลุมด้วยขอบ E 1 , E 2และอี3ซึ่งสามารถแสดงในตารางพื้นผิวรูปหลายเหลี่ยมเป็น S 1 : E 1 , E 2และ E 3
สมการเครื่องบิน
สมการของพื้นผิวระนาบสามารถแสดงเป็น -
ขวาน + By + Cz + D = 0
โดยที่ (x, y, z) คือจุดใด ๆ บนระนาบและสัมประสิทธิ์ A, B, C และ D คือค่าคงที่ที่อธิบายคุณสมบัติเชิงพื้นที่ของเครื่องบิน เราสามารถรับค่าของ A, B, C และ D ได้โดยการแก้ชุดของสมการระนาบสามชุดโดยใช้ค่าพิกัดสำหรับจุดที่ไม่ใช่คอลลิเนียร์สามจุดในระนาบ สมมติว่าจุดยอดสามจุดของระนาบคือ (x 1 , y 1 , z 1 ), (x 2 , y 2 , z 2 ) และ (x 3 , y 3 , z 3 )
ให้เราแก้สมการพร้อมกันต่อไปนี้สำหรับอัตราส่วน A / D, B / D และ C / D คุณจะได้รับค่า A, B, C และ D
(A / D) x 1 + (B / D) y 1 + (C / D) z 1 = -1
(A / D) x 2 + (B / D) y 2 + (C / D) z 2 = -1
(A / D) x 3 + (B / D) y 3 + (C / D) z 3 = -1
เพื่อให้ได้สมการข้างต้นในรูปแบบดีเทอร์มิแนนต์ให้ใช้กฎของแครมเมอร์กับสมการข้างต้น
$A = \begin{bmatrix} 1& y_{1}& z_{1}\\ 1& y_{2}& z_{2}\\ 1& y_{3}& z_{3} \end{bmatrix} B = \begin{bmatrix} x_{1}& 1& z_{1}\\ x_{2}& 1& z_{2}\\ x_{3}& 1& z_{3} \end{bmatrix} C = \begin{bmatrix} x_{1}& y_{1}& 1\\ x_{2}& y_{2}& 1\\ x_{3}& y_{3}& 1 \end{bmatrix} D = - \begin{bmatrix} x_{1}& y_{1}& z_{1}\\ x_{2}& y_{2}& z_{2}\\ x_{3}& y_{3}& z_{3} \end{bmatrix}$
สำหรับจุดใด ๆ (x, y, z) ที่มีพารามิเตอร์ A, B, C และ D เราสามารถพูดได้ว่า -
Ax + By + Cz + D ≠ 0 หมายถึงจุดไม่ได้อยู่บนระนาบ
Ax + By + Cz + D <0 หมายถึงจุดอยู่ภายในพื้นผิว
Ax + By + Cz + D> 0 หมายถึงจุดอยู่นอกพื้นผิว
ตาข่ายรูปหลายเหลี่ยม
พื้นผิว 3 มิติและของแข็งสามารถประมาณได้โดยชุดขององค์ประกอบหลายเหลี่ยมและเส้น พื้นผิวดังกล่าวเรียกว่าpolygonal meshes. ในตาข่ายรูปหลายเหลี่ยมแต่ละขอบจะใช้ร่วมกันโดยไม่เกินสองรูปหลายเหลี่ยม ชุดของรูปหลายเหลี่ยมหรือใบหน้ารวมกันเป็น "ผิวหนัง" ของวัตถุ
วิธีนี้สามารถใช้เพื่อแสดงประเภทของแข็ง / พื้นผิวที่กว้างในกราฟิก ตาข่ายหลายเหลี่ยมสามารถแสดงผลได้โดยใช้อัลกอริธึมการกำจัดพื้นผิวที่ซ่อนอยู่ ตาข่ายรูปหลายเหลี่ยมสามารถแสดงได้สามวิธี -
- การแสดงที่ชัดเจน
- ชี้ไปที่รายการจุดยอด
- ชี้ไปที่รายการขอบ
ข้อดี
- สามารถใช้ในการจำลองวัตถุได้เกือบทุกชนิด
- ง่ายต่อการแสดงเป็นกลุ่มจุดยอด
- แปลงร่างได้ง่าย
- ง่ายต่อการวาดบนหน้าจอคอมพิวเตอร์
ข้อเสีย
- พื้นผิวโค้งสามารถอธิบายได้โดยประมาณเท่านั้น
- เป็นการยากที่จะจำลองวัตถุบางประเภทเช่นเส้นผมหรือของเหลว
เมื่อเราดูภาพที่มีวัตถุและพื้นผิวที่ไม่โปร่งใสเราจะไม่สามารถมองเห็นวัตถุเหล่านั้นจากมุมมองซึ่งอยู่ด้านหลังจากวัตถุที่อยู่ใกล้ตามากขึ้น เราต้องลบพื้นผิวที่ซ่อนอยู่เหล่านี้เพื่อให้ได้ภาพหน้าจอที่สมจริง การระบุและการกำจัดพื้นผิวเหล่านี้เรียกว่าHidden-surface problem.
มีสองวิธีในการขจัดปัญหาพื้นผิวที่ซ่อนอยู่ - Object-Space method และ Image-space method. เมธอด Object-space ถูกนำไปใช้ในระบบพิกัดทางกายภาพและใช้วิธีพื้นที่รูปภาพในระบบพิกัดหน้าจอ
เมื่อเราต้องการแสดงวัตถุ 3 มิติบนหน้าจอ 2 มิติเราจำเป็นต้องระบุส่วนต่างๆของหน้าจอที่มองเห็นได้จากตำแหน่งการรับชมที่เลือก
วิธีการบัฟเฟอร์ความลึก (Z-Buffer)
วิธีนี้พัฒนาโดย Cutmull เป็นแนวทางพื้นที่ภาพ แนวคิดพื้นฐานคือการทดสอบความลึก Z ของแต่ละพื้นผิวเพื่อกำหนดพื้นผิวที่ใกล้เคียงที่สุด (มองเห็นได้)
ในวิธีนี้แต่ละพื้นผิวจะถูกประมวลผลโดยแยกจากกันทีละตำแหน่งพิกเซลบนพื้นผิว ค่าความลึกของพิกเซลจะถูกเปรียบเทียบและพื้นผิว z ที่ใกล้ที่สุด (เล็กที่สุด) จะกำหนดสีที่จะแสดงในเฟรมบัฟเฟอร์
ใช้อย่างมีประสิทธิภาพบนพื้นผิวของรูปหลายเหลี่ยม พื้นผิวสามารถประมวลผลตามลำดับใดก็ได้ หากต้องการลบล้างรูปหลายเหลี่ยมที่อยู่ใกล้กว่าจากรูปไกล ๆ ให้ตั้งชื่อบัฟเฟอร์สองตัวframe buffer และ depth buffer, ใช้
Depth buffer ใช้ในการเก็บค่าความลึกสำหรับตำแหน่ง (x, y) เนื่องจากพื้นผิวถูกประมวลผล (ความลึก 0 ≤≤ 1)
frame buffer ใช้เพื่อเก็บค่าความเข้มของค่าสีในแต่ละตำแหน่ง (x, y)
โดยปกติพิกัด z จะถูกทำให้เป็นมาตรฐานในช่วง [0, 1] ค่า 0 สำหรับพิกัด z ระบุบานหน้าต่างการตัดด้านหลังและ 1 ค่าสำหรับพิกัด z ระบุบานหน้าต่างการตัดด้านหน้า
อัลกอริทึม
Step-1 - ตั้งค่าบัฟเฟอร์ -
ความลึกบัฟเฟอร์ (x, y) = 0
Framebuffer (x, y) = สีพื้นหลัง
Step-2 - ประมวลผลรูปหลายเหลี่ยม (ทีละรูป)
สำหรับตำแหน่งพิกเซลที่ฉาย (x, y) แต่ละตำแหน่งของรูปหลายเหลี่ยมให้คำนวณความลึก z
ถ้า Z> ความลึกบัฟเฟอร์ (x, y)
คำนวณสีพื้นผิว
ตั้งค่าความลึกบัฟเฟอร์ (x, y) = z,
framebuffer (x, y) = สีพื้นผิว (x, y)
ข้อดี
- ใช้งานง่าย
- จะช่วยลดปัญหาความเร็วหากใช้กับฮาร์ดแวร์
- มันประมวลผลทีละวัตถุ
ข้อเสีย
- ต้องใช้หน่วยความจำขนาดใหญ่
- เป็นกระบวนการที่ใช้เวลานาน
วิธีสแกนไลน์
เป็นวิธีการเว้นวรรคภาพเพื่อระบุพื้นผิวที่มองเห็นได้ วิธีนี้มีข้อมูลเชิงลึกสำหรับการสแกนบรรทัดเดียวเท่านั้น ในการกำหนดค่าความลึกของการสแกนหนึ่งบรรทัดเราต้องจัดกลุ่มและประมวลผลรูปหลายเหลี่ยมทั้งหมดที่ตัดกันเส้นสแกนที่กำหนดพร้อมกันก่อนที่จะประมวลผลบรรทัดการสแกนถัดไป ตารางสำคัญสองตารางedge table และ polygon table, ได้รับการบำรุงรักษาสำหรับสิ่งนี้
The Edge Table - ประกอบด้วยจุดสิ้นสุดพิกัดของแต่ละเส้นในฉากความชันผกผันของแต่ละเส้นและตัวชี้ในตารางรูปหลายเหลี่ยมเพื่อเชื่อมต่อขอบกับพื้นผิว
The Polygon Table - ประกอบด้วยค่าสัมประสิทธิ์ระนาบคุณสมบัติของวัสดุพื้นผิวข้อมูลพื้นผิวอื่น ๆ และอาจเป็นตัวชี้ไปยังตารางขอบ

เพื่ออำนวยความสะดวกในการค้นหาพื้นผิวที่ข้ามเส้นสแกนที่กำหนดจะมีการสร้างรายการขอบที่ใช้งานอยู่ รายการที่ใช้งานจะจัดเก็บเฉพาะขอบที่ข้ามเส้นสแกนตามลำดับ x ที่เพิ่มขึ้น นอกจากนี้ยังมีการตั้งค่าสถานะสำหรับแต่ละพื้นผิวเพื่อระบุว่าตำแหน่งตามเส้นสแกนอยู่ด้านในหรือด้านนอกพื้นผิว
ตำแหน่งพิกเซลในแต่ละบรรทัดการสแกนจะถูกประมวลผลจากซ้ายไปขวา ที่จุดตัดด้านซ้ายที่มีพื้นผิวธงพื้นผิวจะเปิดอยู่และที่ด้านขวาธงจะปิด คุณจะต้องทำการคำนวณความลึกก็ต่อเมื่อมีการเปิดแฟล็กหลายพื้นผิวที่ตำแหน่งเส้นสแกนที่กำหนด
วิธีการแบ่งพื้นที่
วิธีการแบ่งพื้นที่ใช้ประโยชน์โดยการหาตำแหน่งพื้นที่มุมมองที่แสดงถึงส่วนหนึ่งของพื้นผิวเดียว แบ่งพื้นที่การรับชมทั้งหมดออกเป็นรูปสี่เหลี่ยมขนาดเล็กและเล็กลงจนกระทั่งแต่ละพื้นที่เล็ก ๆ คือการฉายภาพของส่วนหนึ่งของพื้นผิวที่มองเห็นได้เพียงส่วนเดียวหรือไม่มีพื้นผิวเลย
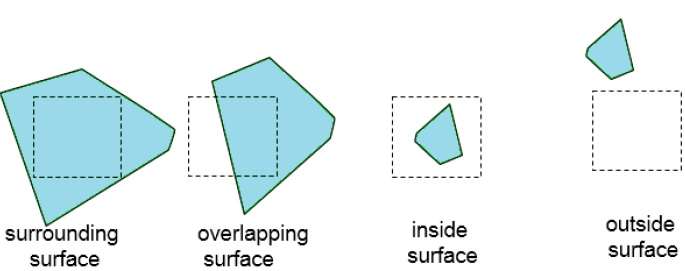
ดำเนินขั้นตอนนี้ต่อไปจนกว่าส่วนย่อยจะได้รับการวิเคราะห์อย่างง่ายดายว่าเป็นของพื้นผิวเดียวหรือจนกว่าจะลดขนาดลงเหลือเพียงพิกเซลเดียว วิธีง่ายๆในการทำเช่นนี้คือแบ่งพื้นที่ออกเป็นสี่ส่วนเท่า ๆ กันในแต่ละขั้นตอน มีความสัมพันธ์ที่เป็นไปได้สี่ประการที่พื้นผิวสามารถมีได้กับขอบเขตพื้นที่ที่ระบุ
Surrounding surface - สิ่งที่ปิดล้อมพื้นที่อย่างสมบูรณ์
Overlapping surface - ส่วนที่อยู่ภายในและบางส่วนนอกพื้นที่
Inside surface - สิ่งที่อยู่ในพื้นที่อย่างสมบูรณ์
Outside surface - สิ่งที่อยู่นอกพื้นที่โดยสิ้นเชิง
การทดสอบเพื่อระบุการมองเห็นพื้นผิวภายในพื้นที่สามารถระบุได้ในรูปแบบของการจำแนกทั้งสี่นี้ ไม่จำเป็นต้องมีการแบ่งย่อยของพื้นที่ที่ระบุอีกต่อไปหากเงื่อนไขใดเงื่อนไขหนึ่งต่อไปนี้เป็นจริง -
- พื้นผิวทั้งหมดเป็นพื้นผิวภายนอกที่เกี่ยวกับพื้นที่
- มีพื้นผิวด้านในซ้อนทับหรือโดยรอบเพียงด้านเดียวเท่านั้นที่อยู่ในพื้นที่
- พื้นผิวโดยรอบบดบังพื้นผิวอื่น ๆ ทั้งหมดภายในขอบเขตพื้นที่
การตรวจจับด้านหลัง
วิธีการเว้นวรรควัตถุที่ง่ายและรวดเร็วในการระบุใบหน้าด้านหลังของรูปทรงหลายเหลี่ยมนั้นขึ้นอยู่กับการทดสอบ "ภายใน - ภายนอก" จุด (x, y, z) คือ "ภายใน" พื้นผิวรูปหลายเหลี่ยมที่มีพารามิเตอร์ระนาบ A, B, C และ D ถ้าเมื่อจุดภายในอยู่ตามแนวสายตากับพื้นผิวรูปหลายเหลี่ยมจะต้องเป็นใบหน้าด้านหลัง ( เราอยู่ข้างในใบหน้านั้นและไม่สามารถมองเห็นด้านหน้าได้จากตำแหน่งการมองของเรา)
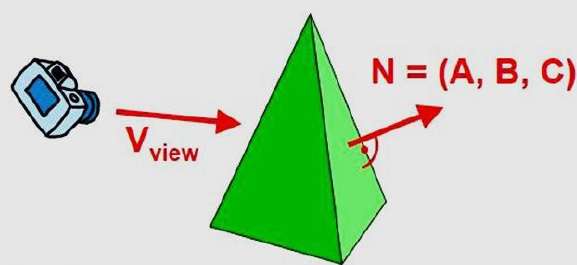
เราสามารถทำให้การทดสอบนี้ง่ายขึ้นโดยพิจารณาจากเวกเตอร์ปกติ N ไปยังพื้นผิวรูปหลายเหลี่ยมซึ่งมีส่วนประกอบของคาร์ทีเซียน (A, B, C)
โดยทั่วไปถ้า V เป็นเวกเตอร์ในทิศทางการมองจากตา (หรือตำแหน่ง "กล้อง") รูปหลายเหลี่ยมนี้จะเป็นหน้าหลังถ้า
V.N > 0
นอกจากนี้หากคำอธิบายวัตถุถูกแปลงเป็นพิกัดการฉายและทิศทางการดูของคุณขนานกับแกน z ที่รับชมแล้ว -
V = (0, 0, V z ) และ V.N = V Z C
ดังนั้นเราต้องพิจารณาสัญลักษณ์ของ C เป็นส่วนประกอบของเวกเตอร์ปกติเท่านั้น N.
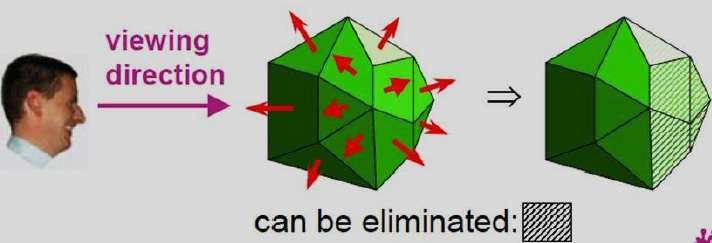
ในระบบการมองด้วยมือขวาที่มีทิศทางการมองไปทางลบ $Z_{V}$แกนรูปหลายเหลี่ยมคือหน้าหลังถ้า C <0 นอกจากนี้เราไม่สามารถมองเห็นใบหน้าใด ๆ ที่ปกติมีองค์ประกอบ z C = 0 เนื่องจากทิศทางการมองของคุณไปทางรูปหลายเหลี่ยมนั้น ดังนั้นโดยทั่วไปเราสามารถติดป้ายรูปหลายเหลี่ยมเป็นหน้าหลังได้ถ้าเวกเตอร์ปกติมีค่าส่วนประกอบ az -
C <= 0
วิธีการที่คล้ายกันนี้สามารถใช้ได้ในแพ็กเกจที่ใช้ระบบการดูด้วยมือซ้าย ในแพ็กเกจเหล่านี้พารามิเตอร์ระนาบ A, B, C และ D สามารถคำนวณได้จากพิกัดจุดยอดรูปหลายเหลี่ยมที่ระบุในทิศทางตามเข็มนาฬิกา (ต่างจากทิศทางทวนเข็มนาฬิกาที่ใช้ในระบบมือขวา)
นอกจากนี้ใบหน้าด้านหลังยังมีเวกเตอร์ปกติที่ชี้อยู่ห่างจากตำแหน่งการมองเห็นและระบุโดย C> = 0 เมื่อทิศทางการรับชมอยู่ในแนวบวก $Z_{v}$แกน. ด้วยการตรวจสอบพารามิเตอร์ C สำหรับระนาบต่างๆที่กำหนดวัตถุเราสามารถระบุใบหน้าด้านหลังทั้งหมดได้ทันที
วิธี A-Buffer
เมธอด A-buffer เป็นส่วนขยายของเมธอด deep-buffer วิธี A-buffer เป็นวิธีการตรวจจับการมองเห็นที่พัฒนาขึ้นที่ Lucas film Studios สำหรับระบบการเรนเดอร์ Renders ทุกสิ่งที่คุณเคยเห็น (REYES)
A-buffer จะขยายในวิธีการบัฟเฟอร์ความลึกเพื่อให้แผ่นใส โครงสร้างข้อมูลหลักใน A-buffer คือบัฟเฟอร์การสะสม
แต่ละตำแหน่งใน A-buffer มีสองฟิลด์ -
Depth field - เก็บจำนวนจริงที่เป็นบวกหรือลบ
Intensity field - เก็บข้อมูลความเข้มของพื้นผิวหรือค่าตัวชี้

ถ้าความลึก> = 0 ตัวเลขที่เก็บไว้ที่ตำแหน่งนั้นคือความลึกของพื้นผิวเดียวที่ทับซ้อนกับพื้นที่พิกเซลที่เกี่ยวข้อง จากนั้นฟิลด์ความเข้มจะเก็บส่วนประกอบ RGB ของสีพื้นผิว ณ จุดนั้นและเปอร์เซ็นต์ของการครอบคลุมพิกเซล
หากความลึก <0 แสดงว่ามีการสนับสนุนหลายพื้นผิวต่อความเข้มของพิกเซล จากนั้นฟิลด์ความเข้มจะจัดเก็บตัวชี้ไปยังรายการข้อมูลพื้นผิวที่เชื่อมโยงกัน บัฟเฟอร์พื้นผิวใน A-buffer ประกอบด้วย -
- ส่วนประกอบความเข้ม RGB
- พารามิเตอร์ความทึบ
- Depth
- เปอร์เซ็นต์ของพื้นที่ครอบคลุม
- ตัวระบุพื้นผิว
อัลกอริทึมดำเนินการเช่นเดียวกับอัลกอริทึมบัฟเฟอร์ความลึก ค่าความลึกและความทึบใช้เพื่อกำหนดสีสุดท้ายของพิกเซล
วิธีการเรียงลำดับความลึก
วิธีการเรียงลำดับความลึกใช้ทั้งการดำเนินการพื้นที่ภาพและพื้นที่วัตถุ วิธีการเรียงลำดับความลึกทำหน้าที่พื้นฐานสองอย่าง -
ขั้นแรกพื้นผิวจะถูกจัดเรียงตามลำดับความลึกที่ลดลง
ประการที่สองพื้นผิวจะถูกแปลงตามลำดับโดยเริ่มจากพื้นผิวที่มีความลึกมากที่สุด
การแปลงการสแกนของพื้นผิวรูปหลายเหลี่ยมจะดำเนินการในพื้นที่ภาพ วิธีการแก้ปัญหาพื้นผิวที่ซ่อนอยู่นี้มักเรียกว่าpainter's algorithm. รูปต่อไปนี้แสดงผลของการเรียงลำดับความลึก -
อัลกอริทึมเริ่มต้นด้วยการจัดเรียงตามความลึก ตัวอย่างเช่นค่าประมาณ "ความลึก" เริ่มต้นของรูปหลายเหลี่ยมอาจถูกนำไปใช้เป็นค่า z ที่ใกล้เคียงที่สุดของจุดยอดใด ๆ ของรูปหลายเหลี่ยม
ให้เรานำรูปหลายเหลี่ยม P ที่ท้ายรายการ พิจารณารูปหลายเหลี่ยมทั้งหมด Q ที่มีส่วนขยาย z ทับซ้อนกันของ P ก่อนวาด P เราทำการทดสอบต่อไปนี้ หากการทดสอบใด ๆ ต่อไปนี้เป็นผลบวกเราสามารถสมมติว่าสามารถวาด P ก่อน Q
- x-extents ไม่ทับซ้อนกันหรือไม่?
- ส่วนขยาย y ไม่ทับซ้อนกันหรือไม่?
- P อยู่ฝั่งตรงข้ามของเครื่องบินของ Q จากมุมมองหรือไม่?
- Q ทั้งหมดอยู่ด้านเดียวกับระนาบของ P กับมุมมองหรือไม่?
- เส้นโครงของรูปหลายเหลี่ยมไม่ทับซ้อนกันหรือไม่?
หากการทดสอบทั้งหมดล้มเหลวเราจะแยก P หรือ Q โดยใช้ระนาบของอีกชุดหนึ่ง รูปหลายเหลี่ยมที่ตัดใหม่จะแทรกเข้าไปในลำดับความลึกและกระบวนการจะดำเนินต่อไป ในทางทฤษฎีการแบ่งพาร์ติชันนี้สามารถสร้าง O (n 2 ) แต่ละรูปหลายเหลี่ยมได้ แต่ในทางปฏิบัติจำนวนรูปหลายเหลี่ยมจะน้อยกว่ามาก
ต้นไม้ Binary Space Partition (BSP)
การแบ่งพื้นที่ไบนารีใช้เพื่อคำนวณการมองเห็น ในการสร้างต้นไม้ BSP ควรเริ่มต้นด้วยรูปหลายเหลี่ยมและติดป้ายกำกับขอบทั้งหมด การจัดการกับขอบเพียงครั้งเดียวให้ขยายขอบแต่ละด้านเพื่อให้ระนาบแยกเป็นสองส่วน วางขอบแรกในต้นไม้เป็นราก เพิ่มขอบตามมาโดยขึ้นอยู่กับว่าอยู่ด้านในหรือด้านนอก ขอบที่ขยายส่วนขยายของขอบที่มีอยู่แล้วในต้นไม้จะถูกแบ่งออกเป็นสองส่วนและทั้งสองจะถูกเพิ่มเข้าไปในต้นไม้

จากรูปด้านบนก่อนอื่น A เป็นราก
ทำรายการโหนดทั้งหมดในรูป (a)
ใส่โหนดทั้งหมดที่อยู่หน้ารูท A ทางด้านซ้ายของโหนด A และใส่โหนดทั้งหมดที่อยู่หลังรูท A ไปทางด้านขวาดังแสดงในรูป (b)
ประมวลผลโหนดด้านหน้าทั้งหมดก่อนแล้วจึงดำเนินการกับโหนดด้านหลัง
ดังแสดงในรูป (c) เราจะประมวลผลโหนดก่อน B. เนื่องจากไม่มีอะไรอยู่หน้าโหนดBเราได้ใส่ NIL อย่างไรก็ตามเรามีโหนดC ที่ด้านหลังของโหนด Bดังนั้นโหนด C จะไปทางด้านขวาของโหนด B.
ทำซ้ำขั้นตอนเดียวกันสำหรับโหนด D.
Dr Benoit Mandelbrot นักคณิตศาสตร์ชาวฝรั่งเศส / อเมริกันได้ค้นพบ Fractals คำว่า Fractal มาจากภาษาละตินคำว่าfractusซึ่งแปลว่าหัก
Fractals คืออะไร?
Fractals เป็นรูปภาพที่ซับซ้อนมากที่สร้างโดยคอมพิวเตอร์จากสูตรเดียว สร้างขึ้นโดยใช้การทำซ้ำ ซึ่งหมายความว่าสูตรหนึ่งจะถูกทำซ้ำโดยมีค่าต่างกันเล็กน้อยซ้ำแล้วซ้ำเล่าโดยคำนึงถึงผลลัพธ์จากการทำซ้ำก่อนหน้านี้
Fractals ถูกใช้ในหลาย ๆ ด้านเช่น -
Astronomy - สำหรับการวิเคราะห์ดาราจักรวงแหวนของดาวเสาร์ ฯลฯ
Biology/Chemistry - สำหรับการวาดภาพวัฒนธรรมของแบคทีเรียปฏิกิริยาทางเคมีกายวิภาคของมนุษย์โมเลกุลพืช
Others - สำหรับการแสดงภาพเมฆแนวชายฝั่งและเส้นขอบการบีบอัดข้อมูลการแพร่กระจายเศรษฐกิจศิลปะเศษส่วนดนตรีเศษส่วนทิวทัศน์เอฟเฟกต์พิเศษ ฯลฯ

การสร้าง Fractals
Fractals สามารถสร้างขึ้นได้โดยการทำซ้ำรูปร่างเดิมซ้ำแล้วซ้ำเล่าดังแสดงในรูปต่อไปนี้ ในรูป (a) แสดงสามเหลี่ยมด้านเท่า ในรูป (b) เราจะเห็นว่าสามเหลี่ยมถูกทำซ้ำเพื่อสร้างรูปร่างคล้ายดาว ในรูป (c) เราจะเห็นว่ารูปดาวในรูป (b) ถูกทำซ้ำครั้งแล้วครั้งเล่าเพื่อสร้างรูปร่างใหม่
เราสามารถทำซ้ำได้ไม่ จำกัด จำนวนเพื่อสร้างรูปร่างที่ต้องการ ในแง่การเขียนโปรแกรมจะใช้การเรียกซ้ำเพื่อสร้างรูปร่างดังกล่าว

เศษส่วนทางเรขาคณิต
เศษส่วนทางเรขาคณิตจัดการกับรูปร่างที่พบในธรรมชาติที่มีขนาดไม่ใช่จำนวนเต็มหรือเศษส่วน ในการสร้างแฟร็กทัลที่คล้ายตัวเองแบบกำหนด (nonrandom) ทางเรขาคณิตเราเริ่มต้นด้วยรูปทรงเรขาคณิตที่กำหนดเรียกว่าinitiator. ส่วนย่อยของผู้ริเริ่มจะถูกแทนที่ด้วยรูปแบบที่เรียกว่าgenerator.

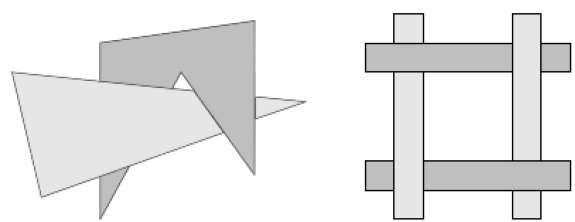
ตัวอย่างเช่นถ้าเราใช้ตัวเริ่มต้นและตัวกำเนิดที่แสดงในรูปด้านบนเราสามารถสร้างรูปแบบที่ดีได้โดยการทำซ้ำ แต่ละส่วนของเส้นตรงในตัวเริ่มต้นจะถูกแทนที่ด้วยส่วนของเส้นตรงที่มีความยาวเท่ากันสี่ส่วนในแต่ละขั้นตอน ตัวคูณมาตราส่วนคือ 1/3 ดังนั้นขนาดเศษส่วนคือ D = ln 4 / ln 3 ≈ 1.2619
นอกจากนี้ความยาวของแต่ละส่วนของเส้นตรงในตัวเริ่มต้นจะเพิ่มขึ้นโดยปัจจัย 4/3 ในแต่ละขั้นตอนเพื่อให้ความยาวของเส้นโค้งเศษส่วนมีแนวโน้มที่จะไม่มีที่สิ้นสุดเมื่อมีการเพิ่มรายละเอียดลงในเส้นโค้งดังแสดงในรูปต่อไปนี้ -
ภาพเคลื่อนไหวหมายถึงการให้ชีวิตแก่วัตถุใด ๆ ในคอมพิวเตอร์กราฟิก มันมีพลังในการฉีดพลังงานและอารมณ์เข้าไปในวัตถุที่ดูเหมือนไม่มีชีวิตมากที่สุด แอนิเมชั่นคอมพิวเตอร์ช่วยและแอนิเมชั่นที่สร้างด้วยคอมพิวเตอร์เป็นแอนิเมชั่นคอมพิวเตอร์สองประเภท สามารถนำเสนอผ่านภาพยนตร์หรือวิดีโอ
แนวคิดพื้นฐานเบื้องหลังภาพเคลื่อนไหวคือการเล่นภาพที่บันทึกไว้ในอัตราที่เร็วพอที่จะหลอกสายตามนุษย์ให้ตีความว่าเป็นการเคลื่อนไหวต่อเนื่อง ภาพเคลื่อนไหวสามารถทำให้ภาพที่ตายแล้วมีชีวิตขึ้นมา แอนิเมชั่นสามารถใช้ในหลาย ๆ ด้านเช่นความบันเทิงการออกแบบโดยใช้คอมพิวเตอร์ช่วยการสร้างภาพทางวิทยาศาสตร์การฝึกอบรมการศึกษาอีคอมเมิร์ซและศิลปะคอมพิวเตอร์
เทคนิคแอนิเมชั่น
แอนิเมเตอร์ได้คิดค้นและใช้เทคนิคแอนิเมชันที่หลากหลาย โดยทั่วไปมีเทคนิคการเคลื่อนไหวหกแบบซึ่งเราจะพูดถึงทีละรายการในส่วนนี้
ภาพเคลื่อนไหวแบบดั้งเดิม (ทีละเฟรม)
ตามเนื้อผ้าแอนิเมชันส่วนใหญ่ทำด้วยมือ เฟรมทั้งหมดในแอนิเมชั่นต้องวาดด้วยมือ เนื่องจากแอนิเมชั่นแต่ละวินาทีต้องใช้ 24 เฟรม (ภาพยนตร์) ความพยายามที่ต้องใช้ในการสร้างภาพยนตร์ที่สั้นที่สุดอาจเป็นจำนวนมาก
คีย์เฟรม
ในเทคนิคนี้จะมีการจัดวางสตอรีบอร์ดจากนั้นศิลปินจะวาดเฟรมหลักของแอนิเมชั่น เฟรมหลักคือเฟรมที่มีการเปลี่ยนแปลงที่โดดเด่นเกิดขึ้น เป็นประเด็นสำคัญของแอนิเมชั่น การกำหนดคีย์เฟรมต้องการให้แอนิเมเตอร์ระบุตำแหน่งวิกฤตหรือตำแหน่งสำคัญสำหรับออบเจ็กต์ จากนั้นคอมพิวเตอร์จะเติมเฟรมที่ขาดหายไปโดยอัตโนมัติโดยการสอดแทรกระหว่างตำแหน่งเหล่านั้นอย่างราบรื่น
ขั้นตอน
ในแอนิเมชั่นขั้นตอนวัตถุจะเคลื่อนไหวโดยกระบวนงานซึ่งเป็นชุดของกฎไม่ใช่โดยการกำหนดคีย์เฟรม แอนิเมเตอร์ระบุกฎและเงื่อนไขเริ่มต้นและเรียกใช้การจำลอง กฎมักเป็นไปตามกฎทางกายภาพของโลกแห่งความเป็นจริงที่แสดงโดยสมการทางคณิตศาสตร์
พฤติกรรม
ในแอนิเมชั่นเชิงพฤติกรรมตัวละครอิสระกำหนดการกระทำของตัวเองอย่างน้อยก็ในระดับหนึ่ง สิ่งนี้ทำให้ตัวละครมีความสามารถในการด้นสดและปลดปล่อยอนิเมเตอร์จากความจำเป็นในการระบุรายละเอียดการเคลื่อนไหวของตัวละครทุกตัว
ตามประสิทธิภาพ (Motion Capture)
อีกเทคนิคหนึ่งคือ Motion Capture ซึ่งเซ็นเซอร์แม่เหล็กหรือการมองเห็นจะบันทึกการกระทำของวัตถุของมนุษย์หรือสัตว์ในรูปแบบสามมิติ จากนั้นคอมพิวเตอร์จะใช้ข้อมูลเหล่านี้เพื่อทำให้วัตถุเคลื่อนไหว
เทคโนโลยีนี้ทำให้นักกีฬาที่มีชื่อเสียงหลายคนสามารถแสดงการกระทำของตัวละครในวิดีโอเกมกีฬาได้ การจับภาพเคลื่อนไหวเป็นที่นิยมในหมู่อนิเมเตอร์ส่วนใหญ่เนื่องจากการกระทำบางอย่างของมนุษย์สามารถจับภาพได้อย่างง่ายดาย อย่างไรก็ตามอาจมีความคลาดเคลื่อนอย่างรุนแรงระหว่างรูปร่างหรือขนาดของวัตถุและตัวแบบกราฟิกและอาจทำให้เกิดปัญหาในการดำเนินการที่แน่นอน
ตามร่างกาย (พลวัต)
ไม่เหมือนกับการจัดเฟรมหลักและภาพเคลื่อนไหวการจำลองใช้กฎของฟิสิกส์เพื่อสร้างการเคลื่อนไหวของภาพและวัตถุอื่น ๆ การจำลองสามารถใช้เพื่อสร้างลำดับที่แตกต่างกันเล็กน้อยได้อย่างง่ายดายในขณะที่ยังคงความสมจริงทางกายภาพ ประการที่สองการจำลองแบบเรียลไทม์อนุญาตให้มีการโต้ตอบในระดับที่สูงขึ้นโดยที่บุคคลจริงสามารถควบคุมการกระทำของตัวละครจำลองได้
ในทางตรงกันข้ามแอปพลิเคชันที่ขึ้นอยู่กับคีย์เฟรมและการเคลื่อนไหวจะเลือกและแก้ไขการเคลื่อนไหวในรูปแบบไลบรารีการเคลื่อนไหวที่คำนวณไว้ล่วงหน้า ข้อเสียเปรียบประการหนึ่งที่การจำลองประสบคือความเชี่ยวชาญและเวลาที่ต้องใช้ในการประดิษฐ์ระบบควบคุมที่เหมาะสม
คีย์เฟรม
คีย์เฟรมคือเฟรมที่เรากำหนดการเปลี่ยนแปลงในภาพเคลื่อนไหว ทุกเฟรมเป็นคีย์เฟรมเมื่อเราสร้างแอนิเมชั่นทีละเฟรม เมื่อมีคนสร้างภาพเคลื่อนไหว 3 มิติบนคอมพิวเตอร์พวกเขามักจะไม่ระบุตำแหน่งที่แน่นอนของวัตถุใด ๆ ในทุกเฟรม พวกเขาสร้างคีย์เฟรม
คีย์เฟรมเป็นเฟรมที่สำคัญในระหว่างที่วัตถุเปลี่ยนขนาดทิศทางรูปร่างหรือคุณสมบัติอื่น ๆ จากนั้นคอมพิวเตอร์จะคำนวณเฟรมที่อยู่ระหว่างกันทั้งหมดและช่วยประหยัดเวลาในการสร้างอนิเมเตอร์ได้มาก ภาพประกอบต่อไปนี้แสดงถึงเฟรมที่วาดโดยผู้ใช้และเฟรมที่สร้างโดยคอมพิวเตอร์


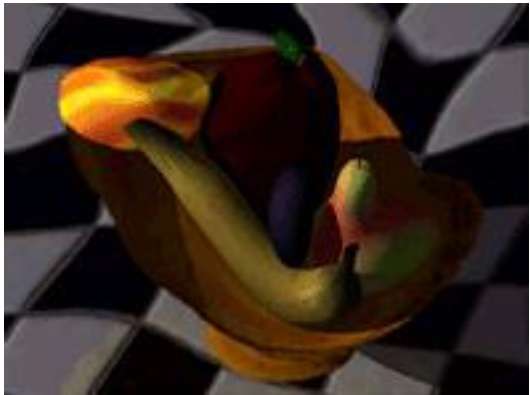
มอร์ฟิง
การเปลี่ยนแปลงรูปร่างของวัตถุจากรูปแบบหนึ่งไปเป็นอีกรูปแบบหนึ่งเรียกว่า morphing เป็นการแปลงร่างที่ซับซ้อนที่สุดครั้งหนึ่ง

มอร์ฟดูราวกับว่าภาพสองภาพหลอมรวมกันด้วยการเคลื่อนไหวที่ลื่นไหลมาก ในแง่เทคนิคภาพสองภาพบิดเบี้ยวและเกิดการซีดจางระหว่างทั้งสองภาพ