อัลกอริทึมการสร้างวงกลม

การวาดวงกลมบนหน้าจอนั้นซับซ้อนกว่าการวาดเส้นเล็กน้อย มีสองอัลกอริทึมยอดนิยมในการสร้างวงกลม -Bresenham’s Algorithm และ Midpoint Circle Algorithm. อัลกอริทึมเหล่านี้ขึ้นอยู่กับแนวคิดในการกำหนดจุดต่อมาที่จำเป็นในการวาดวงกลม ให้เราหารือเกี่ยวกับอัลกอริทึมโดยละเอียด -

สมการของวงกลมคือ $ X ^ {2} + Y ^ {2} = r ^ {2} $ โดยที่ r คือรัศมี

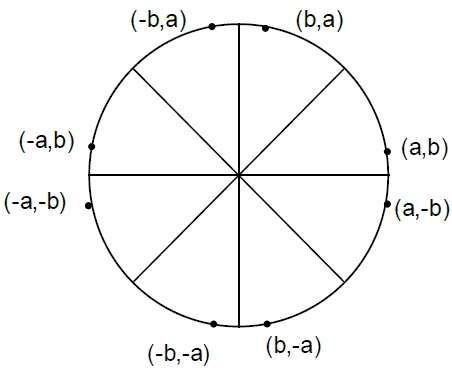
อัลกอริทึมของ Bresenham

เราไม่สามารถแสดงส่วนโค้งต่อเนื่องบนจอแสดงผลแบบแรสเตอร์ได้ แต่เราต้องเลือกตำแหน่งพิกเซลที่ใกล้ที่สุดเพื่อให้ส่วนโค้งสมบูรณ์

จากภาพประกอบต่อไปนี้คุณจะเห็นว่าเราวางพิกเซลไว้ที่ตำแหน่ง (X, Y) และตอนนี้ต้องตัดสินใจว่าจะวางพิกเซลต่อไปที่ใด - ที่ N (X + 1, Y) หรือที่ S (X + 1, Y-1)

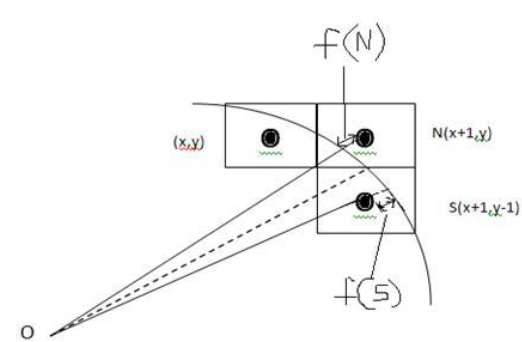
สิ่งนี้สามารถตัดสินใจได้โดยพารามิเตอร์การตัดสินใจ d.

• ถ้า d <= 0 ดังนั้น N (X + 1, Y) จะถูกเลือกเป็นพิกเซลถัดไป
• ถ้า d> 0 ดังนั้น S (X + 1, Y-1) จะถูกเลือกเป็นพิกเซลถัดไป

อัลกอริทึม

Step 1- รับพิกัดของจุดศูนย์กลางของวงกลมและรัศมีและเก็บไว้ใน x, y และ R ตามลำดับ ตั้งค่า P = 0 และ Q = R

Step 2 - ตั้งค่าพารามิเตอร์การตัดสินใจ D = 3 - 2R

Step 3 - ทำซ้ำจนถึงขั้นตอนที่ 8 ในขณะที่ P ≤ Q.

Step 4 - โทรวาดวงกลม (X, Y, P, Q)

Step 5 - เพิ่มมูลค่าของ P.

Step 6 - ถ้า D <0 แล้ว D = D + 4P + 6

Step 7 - ชุดอื่น R = R - 1, D = D + 4 (PQ) + 10

Step 8 - โทรวาดวงกลม (X, Y, P, Q)

Draw Circle Method(X, Y, P, Q).

Call Putpixel (X + P, Y + Q).
Call Putpixel (X - P, Y + Q).
Call Putpixel (X + P, Y - Q).
Call Putpixel (X - P, Y - Q).
Call Putpixel (X + Q, Y + P).
Call Putpixel (X - Q, Y + P).
Call Putpixel (X + Q, Y - P).
Call Putpixel (X - Q, Y - P).

อัลกอริทึมจุดกึ่งกลาง

Step 1 - รัศมีอินพุต r และวงกลมตรงกลาง $ (x_ {c,} y_ {c}) $ และรับจุดแรกบนเส้นรอบวงของวงกลมที่มีศูนย์กลางอยู่ที่จุดกำเนิดเป็น

(x0, y0) = (0, r)

Step 2 - คำนวณค่าเริ่มต้นของพารามิเตอร์การตัดสินใจเป็น

$ P_ {0} $ = 5/4 - r (ดูคำอธิบายต่อไปนี้สำหรับการทำให้สมการนี้ง่ายขึ้น)

f(x, y) = x2 + y2 - r2 = 0

f(xi - 1/2 + e, yi + 1)
        = (xi - 1/2 + e)2 + (yi + 1)2 - r2 
        = (xi- 1/2)2 + (yi + 1)2 - r2 + 2(xi - 1/2)e + e2
        = f(xi - 1/2, yi + 1) + 2(xi - 1/2)e + e2 = 0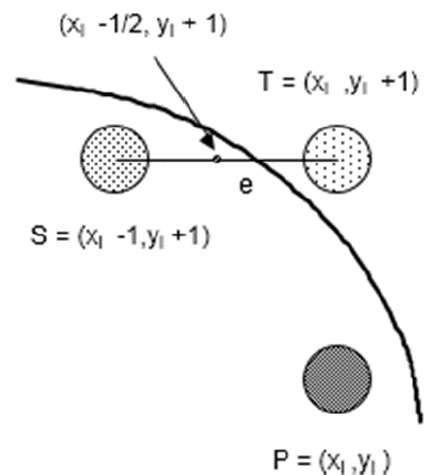

Let di = f(xi - 1/2, yi + 1) = -2(xi - 1/2)e - e2
Thus,

If e < 0 then di > 0 so choose point S = (xi - 1, yi + 1).
di+1    = f(xi - 1 - 1/2, yi + 1 + 1) = ((xi - 1/2) - 1)2 + ((yi + 1) + 1)2 - r2
        = di - 2(xi - 1) + 2(yi + 1) + 1
        = di + 2(yi + 1 - xi + 1) + 1
		  
If e >= 0 then di <= 0 so choose point T = (xi, yi + 1)
   di+1 = f(xi - 1/2, yi + 1 + 1)
       = di + 2yi+1 + 1
		  
The initial value of di is
   d0 = f(r - 1/2, 0 + 1) = (r - 1/2)2 + 12 - r2
      = 5/4 - r {1-r can be used if r is an integer}
		
When point S = (xi - 1, yi + 1) is chosen then
   di+1 = di + -2xi+1 + 2yi+1 + 1
	
When point T = (xi, yi + 1) is chosen then
   di+1 = di + 2yi+1 + 1

Step 3 - ในแต่ละตำแหน่ง $ X_ {K} $ เริ่มต้นที่ K = 0 ให้ทำการทดสอบต่อไปนี้ -

If PK < 0 then next point on circle (0,0) is (XK+1,YK) and
   PK+1 = PK + 2XK+1 + 1
Else
   PK+1 = PK + 2XK+1 + 1 – 2YK+1
	
Where, 2XK+1 = 2XK+2 and 2YK+1 = 2YK-2.

Step 4 - กำหนดจุดสมมาตรในอีกเจ็ดแปด

Step 5 - ย้ายตำแหน่งพิกเซลในการคำนวณ (X, Y) ไปยังเส้นทางวงกลมที่มีศูนย์กลางอยู่ที่ $ (X_ {C,} Y_ {C}) $ และพล็อตค่าพิกัด

X = X + XC,   Y = Y + YC

Step 6 - ทำซ้ำขั้นตอนที่ 3 ถึง 5 จนถึง X> = Y