วงจรเลขคณิตดิจิทัล
ในบทนี้ให้เราพูดคุยเกี่ยวกับวงจรเลขคณิตพื้นฐานเช่น Binary adder และ Binary subtractor วงจรเหล่านี้สามารถทำงานได้ด้วยค่าไบนารี 0 และ 1
ไบนารีแอดเดอร์
การคำนวณทางคณิตศาสตร์ขั้นพื้นฐานที่สุดคือการบวก วงจรซึ่งดำเนินการเพิ่มเลขฐานสองสองตัวเรียกว่าBinary adder. ขั้นแรกให้เราใช้ adder ซึ่งทำการเพิ่มสองบิต
ครึ่งแอดเดอร์
Half adder เป็นวงจรรวมซึ่งทำหน้าที่เพิ่มเลขฐานสองสองตัว A และ B เป็นของ single bit. มันสร้างผลรวมสองเอาท์พุต S & carry, C.
Truth table ของ Half adder แสดงอยู่ด้านล่าง
| อินพุต | เอาท์พุต | ||
|---|---|---|---|
| ก | ข | ค | ส |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
เมื่อเราทำการบวกสองบิตผลรวมที่เป็นผลลัพธ์จะมีค่าตั้งแต่ 0 ถึง 2 เป็นทศนิยม เราสามารถแทนทศนิยมหลัก 0 และ 1 ด้วยบิตเดียวในไบนารี แต่เราไม่สามารถแทนทศนิยม 2 หลักด้วยบิตเดียวในไบนารี ดังนั้นเราจึงต้องการสองบิตในการแสดงเป็นไบนารี
ให้ผลรวม S เป็นบิตที่มีนัยสำคัญน้อยที่สุดและดำเนินการ C คือบิตที่สำคัญที่สุดของผลรวมผลลัพธ์ สำหรับอินพุตสามชุดแรกพกพา C คือศูนย์และค่าของ S จะเป็นศูนย์หรือหนึ่งตามnumber of onesนำเสนอที่อินพุต แต่สำหรับการรวมกันครั้งสุดท้ายของอินพุตให้พกพา C คือหนึ่งและผลรวม S เป็นศูนย์เนื่องจากผลรวมผลลัพธ์เป็นสอง
จากตารางความจริงเราสามารถเขียนไฟล์ Boolean functions สำหรับแต่ละเอาต์พุตเป็น
$$ S = A \ oplus B $$
$ C = AB $
เราสามารถใช้ฟังก์ชันข้างต้นด้วย Ex-OR gate 2-input & 2-input AND gate circuit diagram ของ Half adder แสดงดังรูปต่อไปนี้

ในวงจรด้านบนประตู Ex-OR สองอินพุทและสองอินพุท AND ประตูจะสร้างผลรวม, S & พก, C ตามลำดับ ดังนั้น Half-adder จึงทำการเพิ่มสองบิต
แอดเต็ม
Full adder เป็นวงจรผสมซึ่งทำหน้าที่ addition of three bitsA, B และ C ใน โดยที่ A & B คือบิตสำคัญสองตัวที่ขนานกันและ C inคือบิตพกพาซึ่งสร้างขึ้นจากขั้นตอนก่อนหน้า Full adder นี้ยังสร้างผลรวมสองเอาต์พุต S & carry, C outซึ่งคล้ายกับ Half adder
Truth table ของแอดเดอร์เต็มแสดงอยู่ด้านล่าง
| อินพุต | เอาท์พุต | |||
|---|---|---|---|---|
| A | B | Cin | Cout | S |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
เมื่อเราทำการบวกสามบิตผลรวมที่เป็นผลลัพธ์จะมีค่าตั้งแต่ 0 ถึง 3 เป็นทศนิยม เราสามารถแทนทศนิยมหลัก 0 และ 1 ด้วยบิตเดียวในไบนารี แต่เราไม่สามารถแทนค่าทศนิยม 2 และ 3 ด้วยบิตเดียวในไบนารีได้ ดังนั้นเราจึงต้องการสองบิตสำหรับแทนทศนิยมสองหลักในไบนารี
ให้ผลรวม S เป็นบิตที่มีนัยสำคัญน้อยที่สุดและดำเนินการ C ออกเป็นบิตที่สำคัญที่สุดของผลรวมผลลัพธ์ ง่ายต่อการกรอกค่าของเอาต์พุตสำหรับชุดค่าผสมของอินพุตทั้งหมดในตารางความจริง เพียงแค่นับnumber of onesแสดงที่อินพุตและเขียนเลขฐานสองที่เท่ากันที่เอาต์พุต ถ้า C inเท่ากับศูนย์ตารางความจริงของแอดเดอร์เต็มจะเหมือนกับตารางความจริงของแอดเดอร์ครึ่งหนึ่ง
เราจะได้รับสิ่งต่อไปนี้ Boolean functions สำหรับแต่ละเอาต์พุตหลังจากการทำให้เข้าใจง่าย
$$ S = A \ oplus B \ oplus C_ {in} $$
$ c_ {out} = AB + \ left (A \ oplus B \ right) c_ {in} $
ผลรวม S เท่ากับหนึ่งเมื่อมีจำนวนคี่ที่อินพุต เรารู้ว่า Ex-OR gate สร้างเอาต์พุตซึ่งเป็นฟังก์ชันแปลก ๆ ดังนั้นเราสามารถใช้ประตู Ex-OR 2 อินพุทสองประตูหรือประตู Ex-OR 3 อินพุทหนึ่งช่องเพื่อสร้างผลรวม S. เราสามารถใช้การดำเนินการ C ออกโดยใช้ 2 อินพุต 2 ประตูและประตูหนึ่งหรือประตูหนึ่งหรือ circuit diagram ของ Full adder แสดงดังรูปต่อไปนี้
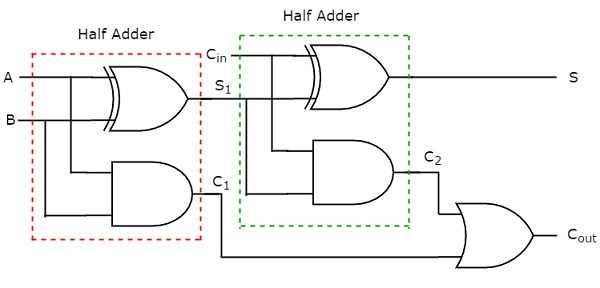
แอดเดอร์นี้เรียกว่า Full adderเนื่องจากในการใช้งาน Full adder หนึ่งตัวเราต้องใช้ Half adders สองตัวและหนึ่งประตู OR ถ้า C inเป็นศูนย์ดังนั้น Full adder จะกลายเป็น Half adder เราสามารถตรวจสอบได้อย่างง่ายดายจากแผนภาพวงจรด้านบนหรือจากฟังก์ชันบูลีนของเอาต์พุตของ Full adder
แอดเดอร์ไบนารี 4 บิต
แอดเดอร์ไบนารี 4 บิตทำหน้าที่ addition of two 4-bit numbers. ให้เลขฐานสอง 4 บิตคือ $ A = A_ {3} A_ {2} A_ {1} A_ {0} $ และ $ B = B_ {3} B_ {2} B_ {1} B_ {0} $ เราสามารถนำไบนารีแอดเดอร์ 4 บิตมาใช้ด้วยวิธีใดวิธีหนึ่งดังต่อไปนี้
ใช้ Half adder หนึ่งตัวในการเพิ่มบิตที่มีนัยสำคัญน้อยสองตัวและตัวเติมเต็มสามตัวสำหรับการเพิ่มบิตที่มีนัยสำคัญสูงกว่าสาม
ใช้ตัวเติมเต็มสี่ตัวเพื่อความสม่ำเสมอ เนื่องจากการดำเนินการเริ่มต้น C ในเป็นศูนย์ adder เต็มซึ่งใช้สำหรับการเพิ่มบิตที่มีนัยสำคัญน้อยที่สุดจึงกลายเป็น Half adder
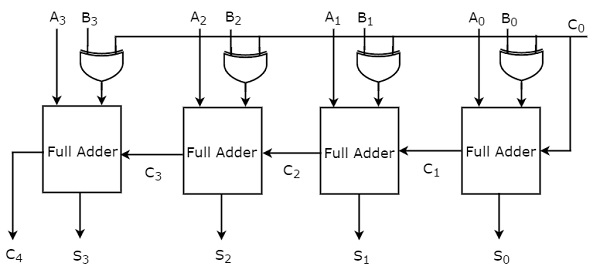
ในขณะนี้เราได้พิจารณาแนวทางที่สอง block diagram ของแอดเดอร์ไบนารี 4 บิตแสดงดังรูปต่อไปนี้

ที่นี่แอดเดอร์ตัวเต็ม 4 ตัวเรียงซ้อนกัน Full adder แต่ละตัวจะได้รับบิตตามลำดับของอินพุตแบบขนานสองตัว A & B เอาต์พุตพกพาของ Full adder หนึ่งตัวจะเป็นอินพุต carry ของ Full adder ลำดับที่สูงกว่าในภายหลัง ไบนารีแอดเดอร์ 4 บิตนี้สร้างผลรวมผลลัพธ์ที่มีมากที่สุด 5 บิต ดังนั้นการดำเนินการขั้นตอนสุดท้าย Full adder จะเป็น MSB
ด้วยวิธีนี้เราสามารถใช้ไบนารีแอดเดอร์ลำดับที่สูงขึ้นได้เพียงแค่เรียงซ้อนตามจำนวนที่ต้องการของแอดเดอร์เต็ม ไบนารีแอดเดอร์นี้เรียกอีกอย่างว่าripple carry (binary) adder เนื่องจากการพกพาแพร่กระจาย (ระลอกคลื่น) จากขั้นตอนหนึ่งไปยังขั้นถัดไป
ตัวลบไบนารี
วงจรซึ่งทำการลบเลขฐานสองสองตัวเรียกว่า Binary subtractor. เราสามารถใช้ตัวลบไบนารีในสองวิธีต่อไปนี้
- Cascade ตัวลบแบบเต็ม
- วิธีการเสริม 2
ในวิธีแรกเราจะได้ตัวลบไบนารี n-bit โดยการเรียงซ้อน 'n' ตัวลบเต็ม ดังนั้นก่อนอื่นคุณสามารถใช้ตัวลบครึ่งหนึ่งและตัวลบเต็มได้ซึ่งคล้ายกับ Half adder & Full adder จากนั้นคุณสามารถใช้ตัวลบไบนารี n-bit โดยการเรียงซ้อน 'n' ตัวลบแบบเต็ม ดังนั้นเราจะมีสองวงจรแยกกันสำหรับการบวกและการลบเลขฐานสองสองเลขฐานสอง
ในวิธีที่สองเราสามารถใช้ไบนารีแอดเดอร์เดียวกันสำหรับการลบเลขฐานสองสองตัวโดยทำการแก้ไขบางอย่างในอินพุตที่สอง ดังนั้นการดำเนินการเพิ่มไบนารีภายในจึงเกิดขึ้น แต่ผลลัพธ์คือการลบผลลัพธ์
เรารู้ว่าการลบเลขฐานสอง A & B สองตัวสามารถเขียนเป็น
$$ AB = A + \ left ({2} ของ \: คำชม \: จาก \: B \ right) $$
$ \ Rightarrow AB = A + \ left ({1} ของ \: ชมเชย \: ของ \: B \ right) + 1 $
ตัวลบไบนารี 4 บิต
ตัวลบไบนารี 4 บิตสร้างไฟล์ subtraction of two 4-bit numbers. ให้เลขฐานสอง 4 บิตคือ $ A = A_ {3} A_ {2} A_ {1} A_ {0} $ และ $ B = B_ {3} B_ {2} B_ {1} B_ {0} $ ภายในการดำเนินการของตัวลบไบนารี 4 บิตจะคล้ายกับตัวเพิ่มไบนารี 4 บิต ถ้าบิตปกติของเลขฐานสอง A, บิตเสริมของเลขฐานสอง B และค่าเริ่มต้น (ยืม), C ในเป็นหนึ่งจะถูกนำไปใช้กับตัวเพิ่มไบนารี 4 บิตมันจะกลายเป็นตัวลบไบนารี 4 บิต block diagram ของตัวลบไบนารี 4 บิตแสดงในรูปต่อไปนี้

ตัวลบไบนารี 4 บิตนี้สร้างเอาต์พุตซึ่งมีไม่เกิน 5 บิต ถ้าเลขฐานสอง A มากกว่าเลขฐานสอง B ดังนั้น MSB ของผลลัพธ์จะเป็นศูนย์และบิตที่เหลือจะมีขนาดของ AB ถ้าเลขฐานสอง A น้อยกว่าเลขฐานสอง B MSB ของผลลัพธ์จะเป็นหนึ่ง เอาเอาท์พุต 2 ส่วนมาเสริมเพื่อให้ได้ขนาดของ AB
ด้วยวิธีนี้เราสามารถใช้ตัวลบไบนารีลำดับที่สูงกว่าได้เพียงแค่เรียงซ้อนจำนวนแอดเดอร์เต็มที่ต้องการพร้อมการปรับเปลี่ยนที่จำเป็น
Binary Adder / Subtractor
วงจรซึ่งสามารถใช้เพื่อทำการบวกหรือลบเลขฐานสองสองตัวได้ตลอดเวลาเรียกว่า Binary Adder / subtractor. ทั้งสองตัวแอดเดอร์แบบไบนารีและตัวลบไบนารีประกอบด้วยชุดของตัวเติมเต็มซึ่งเรียงซ้อนกัน บิตอินพุตของเลขฐานสอง A ถูกนำไปใช้โดยตรงทั้งในตัวเพิ่มไบนารีและตัวลบไบนารี
มีความแตกต่างสองประการในอินพุตของตัวเพิ่มแบบเต็มที่มีอยู่ในตัวเพิ่มไบนารีและตัวลบไบนารี
บิตอินพุตของเลขฐานสอง B ถูกนำไปใช้โดยตรงกับตัวเติมเต็มในตัวเพิ่มไบนารีในขณะที่บิตเสริมของเลขฐานสอง B ถูกนำไปใช้กับตัวเติมเต็มในตัวลบไบนารี
การพกพาเริ่มต้น C 0 = 0 ถูกนำไปใช้ในตัวเพิ่มไบนารี 4 บิตในขณะที่การพกพาเริ่มต้น (ยืม) C 0 = 1 ถูกนำไปใช้ในตัวลบไบนารี 4 บิต
เรารู้ว่าก 2-input Ex-OR gateสร้างเอาต์พุตซึ่งเหมือนกับอินพุตแรกเมื่ออินพุตอื่นเป็นศูนย์ ในทำนองเดียวกันจะสร้างเอาต์พุตซึ่งเป็นส่วนเสริมของอินพุตแรกเมื่ออินพุตอื่นเป็นหนึ่ง
ดังนั้นเราสามารถใช้บิตอินพุตของเลขฐานสอง B กับประตู Ex-OR 2 อินพุต ป้อนข้อมูลอื่น ๆ ทั้งหมดเหล่านี้อดีตหรือประตูคือ C 0 ดังนั้นตามค่าของ C 0ประตู Ex-OR จะสร้างบิตปกติหรือส่วนเสริมของเลขฐานสอง B
4-bit Binary Adder / Subtractor
4 บิตบวกไบนารี / ตัวลบผลิตทั้งเพิ่มหรือลบของตัวเลขสอง 4 บิตขึ้นอยู่กับมูลค่าของการดำเนินการครั้งแรกหรือยืมที่0 ให้เลขฐานสอง 4 บิตคือ $ A = A_ {3} A_ {2} A_ {1} A_ {0} $ และ $ B = B_ {3} B_ {2} B_ {1} B_ {0} $ การดำเนินการของ 4-bit Binary adder / subtractor นั้นคล้ายกับของ Binary adder 4-bit และตัวลบ Binary 4-bit
ใช้บิตปกติของเลขฐานสอง A และ B และการพกพาหรือยืมเริ่มต้น C 0จากภายนอกเป็นไบนารีแอดเดอร์ 4 บิต block diagram ของแอดเดอร์ / ตัวลบไบนารี 4 บิตแสดงในรูปต่อไปนี้
หากการดำเนินการเริ่มต้น0เป็นศูนย์ดังนั้นตัวเพิ่มเต็มแต่ละตัวจะได้รับบิตปกติของเลขฐานสอง A & B ดังนั้นตัวเพิ่ม / ตัวลบไบนารี 4 บิตจะสร้างเอาต์พุตซึ่งก็คือaddition of two binary numbers เอแอนด์บี
หากการยืมครั้งแรก0เป็นหนึ่งดังนั้นตัวเพิ่มเต็มแต่ละตัวจะได้รับบิตปกติของเลขฐานสอง A และบิตเสริมของเลขฐานสอง B ดังนั้นตัวเพิ่ม / ตัวลบไบนารี 4 บิตจะสร้างผลลัพธ์ซึ่งก็คือsubtraction of two binary numbers เอแอนด์บี
ดังนั้นด้วยความช่วยเหลือของประตู Ex-OR เพิ่มเติมสามารถใช้วงจรเดียวกันสำหรับการบวกและการลบเลขฐานสองสองตัว