การสร้างแบบจำลองการหารจำนวนเต็มโดยเศษส่วน
ในบทเรียนนี้เราได้เรียนรู้วิธีใช้แบบจำลองพื้นที่เพื่อหารจำนวนเต็มด้วยเศษส่วน มีจำนวนเต็มและเศษส่วนที่หารจำนวนเต็มนั้น เราพิจารณาจำนวนเต็มเป็นสี่เหลี่ยมจำนวนมากตามที่ตัวเลขระบุเราแบ่งแต่ละกำลังสองออกเป็นหลายส่วนตามที่ตัวส่วนของเศษส่วนระบุ เราหาผลลัพธ์ของการหารนี้โดยการนับจำนวนส่วนทั้งหมดของกำลังสอง
Example:
หาร 3 ÷ $ \ frac {1} {2} $โดยใช้แบบจำลองพื้นที่
Solution
Step 1:
จำนวนเต็ม 3 ถูกนำมาเป็นสามกำลังสอง เนื่องจากเศษส่วนเป็นครึ่งหนึ่งแต่ละสี่เหลี่ยมจะถูกแบ่งออกเป็นสองส่วน
Step 2:
ตอนนี้แบ่งเท่า ๆ กันในทั้งสามสี่เหลี่ยมจะนับและพบว่าเป็น 6. นี่คือคำตอบที่เราได้รับโดยการหาร 3 โดย$ \ frac {1} {2} $
ดังนั้น 3 ÷ $ \ frac {1} {2} $ = 6
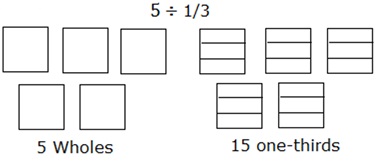
หาร 5 ÷ $ \ frac {1} {3} $โดยใช้แบบจำลองพื้นที่
วิธีการแก้
Step 1:
การหาร 5 เป็นหนึ่งในสามสามารถจำลองได้ดังนี้:
พิจารณา 5 สี่เหลี่ยมเป็น 5 wholes แต่ละช่องจะแบ่งออกเป็นสามส่วนหรือหนึ่งในสาม
Step 2:
จากนั้นนับจำนวนรวมของส่วนดังกล่าวของกำลังสองหรือ Wholes จะได้คำตอบซึ่งก็คือ 15
ดังนั้น 5 ÷ $ \ frac {1} {3} $ = 15
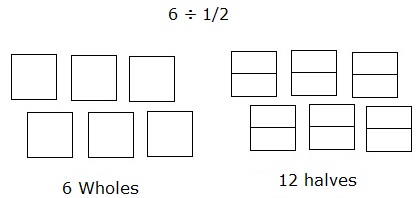
หาร 6 ÷ $ \ frac {1} {2} $โดยใช้แบบจำลองพื้นที่
วิธีการแก้
Step 1:
การแบ่ง 6 ออกเป็นครึ่งเดียวสามารถสร้างแบบจำลองได้ดังนี้:
พิจารณา 6 เหลี่ยมเป็น 6 wholes แต่ละสี่เหลี่ยมจะถูกแบ่งออกเป็นสองส่วนหรือครึ่งหนึ่ง
Step 2:
จากนั้นนับจำนวนรวมของส่วนดังกล่าวของกำลังสองหรือ Wholes จะได้คำตอบซึ่งเป็น 12
ดังนั้น 6 ÷ $ \ frac {1} {2} $ = 12