Künstliches Neuronales Netz - Bausteine

Die Verarbeitung von ANN hängt von den folgenden drei Bausteinen ab:

Netzwerktopologie
Gewichtsanpassungen oder Lernen
Aktivierungsfunktionen

In diesem Kapitel werden wir diese drei Bausteine von ANN ausführlich diskutieren

Netzwerktopologie

Eine Netzwerktopologie ist die Anordnung eines Netzwerks zusammen mit seinen Knoten und Verbindungslinien. Entsprechend der Topologie kann ANN wie folgt klassifiziert werden:

Feedforward-Netzwerk

Es ist ein nicht wiederkehrendes Netzwerk mit Verarbeitungseinheiten / Knoten in Schichten, und alle Knoten in einer Schicht sind mit den Knoten der vorherigen Schichten verbunden. Die Verbindung hat unterschiedliche Gewichte. Es gibt keine Rückkopplungsschleife, dh das Signal kann nur in eine Richtung von Eingang zu Ausgang fließen. Es kann in die folgenden zwei Typen unterteilt werden -

Single layer feedforward network- Das Konzept besteht darin, dass Feedforward-ANN nur eine gewichtete Schicht aufweist. Mit anderen Worten können wir sagen, dass die Eingabeschicht vollständig mit der Ausgabeschicht verbunden ist.

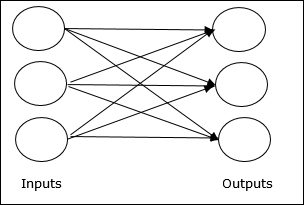
Multilayer feedforward network- Das Konzept besteht darin, dass Feedforward-ANN mehr als eine gewichtete Schicht aufweist. Da dieses Netzwerk eine oder mehrere Schichten zwischen der Eingabe- und der Ausgabeschicht hat, wird es als versteckte Schichten bezeichnet.

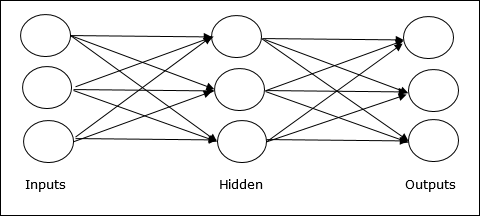
Feedback-Netzwerk

Wie der Name schon sagt, verfügt ein Rückkopplungsnetzwerk über Rückkopplungspfade, was bedeutet, dass das Signal mithilfe von Schleifen in beide Richtungen fließen kann. Dies macht es zu einem nichtlinearen dynamischen System, das sich kontinuierlich ändert, bis es einen Gleichgewichtszustand erreicht. Es kann in die folgenden Typen unterteilt werden:

Recurrent networks- Sie sind Rückkopplungsnetzwerke mit geschlossenen Schleifen. Im Folgenden sind die beiden Arten von wiederkehrenden Netzwerken aufgeführt.
Fully recurrent network - Dies ist die einfachste neuronale Netzwerkarchitektur, da alle Knoten mit allen anderen Knoten verbunden sind und jeder Knoten sowohl als Eingabe als auch als Ausgabe fungiert.

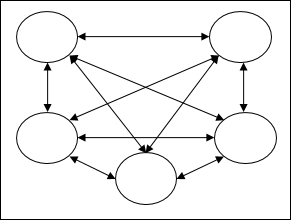
Jordan network - Es handelt sich um ein Netzwerk mit geschlossenem Regelkreis, in dem der Ausgang als Rückmeldung wieder an den Eingang geht, wie in der folgenden Abbildung dargestellt.

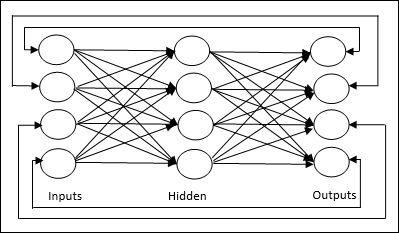
Gewichtsanpassungen oder Lernen

Lernen in einem künstlichen neuronalen Netzwerk ist die Methode zum Ändern der Verbindungsgewichte zwischen den Neuronen eines bestimmten Netzwerks. Das Lernen in ANN kann in drei Kategorien eingeteilt werden, nämlich überwachtes Lernen, unbeaufsichtigtes Lernen und verstärkendes Lernen.

Überwachtes Lernen

Wie der Name schon sagt, wird diese Art des Lernens unter der Aufsicht eines Lehrers durchgeführt. Dieser Lernprozess ist abhängig.

Während des Trainings von ANN unter überwachtem Lernen wird der Eingabevektor dem Netzwerk präsentiert, das einen Ausgabevektor ergibt. Dieser Ausgabevektor wird mit dem gewünschten Ausgabevektor verglichen. Ein Fehlersignal wird erzeugt, wenn zwischen dem tatsächlichen Ausgang und dem gewünschten Ausgangsvektor ein Unterschied besteht. Auf der Grundlage dieses Fehlersignals werden die Gewichte angepasst, bis die tatsächliche Ausgabe mit der gewünschten Ausgabe übereinstimmt.

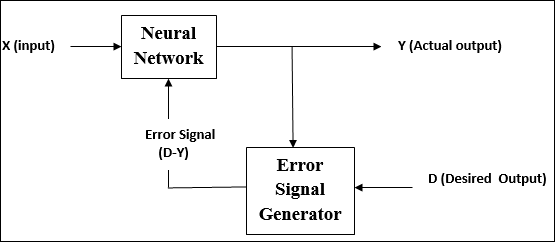
Unbeaufsichtigtes Lernen

Wie der Name schon sagt, wird diese Art des Lernens ohne Aufsicht eines Lehrers durchgeführt. Dieser Lernprozess ist unabhängig.

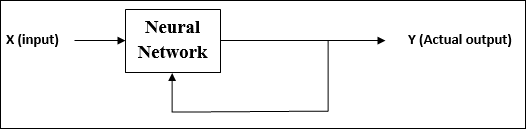
Während des Trainings von ANN unter unbeaufsichtigtem Lernen werden die Eingabevektoren ähnlichen Typs zu Clustern kombiniert. Wenn ein neues Eingabemuster angewendet wird, gibt das neuronale Netzwerk eine Ausgabeantwort aus, die die Klasse angibt, zu der das Eingabemuster gehört.

Es gibt keine Rückmeldung von der Umgebung, welche Ausgabe gewünscht werden soll und ob sie richtig oder falsch ist. Daher muss bei dieser Art des Lernens das Netzwerk selbst die Muster und Merkmale aus den Eingabedaten und die Beziehung für die Eingabedaten über die Ausgabe ermitteln.

Verstärkungslernen

Wie der Name schon sagt, wird diese Art des Lernens verwendet, um das Netzwerk über einige kritische Informationen zu stärken oder zu stärken. Dieser Lernprozess ähnelt dem überwachten Lernen, wir haben jedoch möglicherweise weniger Informationen.

Während des Trainings des Netzwerks unter verstärkendem Lernen erhält das Netzwerk einige Rückmeldungen aus der Umgebung. Dies macht es dem überwachten Lernen etwas ähnlich. Das hier erhaltene Feedback ist jedoch bewertend und nicht lehrreich, was bedeutet, dass es keinen Lehrer wie beim überwachten Lernen gibt. Nach Erhalt des Feedbacks nimmt das Netzwerk Anpassungen der Gewichte vor, um in Zukunft bessere Kritikerinformationen zu erhalten.

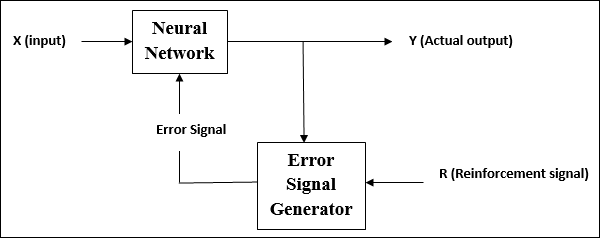
Aktivierungsfunktionen

Es kann als die zusätzliche Kraft oder Anstrengung definiert werden, die auf die Eingabe ausgeübt wird, um eine genaue Ausgabe zu erhalten. In ANN können wir auch Aktivierungsfunktionen auf den Eingang anwenden, um den genauen Ausgang zu erhalten. Im Folgenden sind einige interessante Aktivierungsfunktionen aufgeführt:

Lineare Aktivierungsfunktion

Es wird auch als Identitätsfunktion bezeichnet, da keine Eingabebearbeitung durchgeführt wird. Es kann definiert werden als -

$$ F (x) \: = \: x $$

Sigmoid-Aktivierungsfunktion

Es ist von zwei Arten wie folgt -

Binary sigmoidal function- Diese Aktivierungsfunktion führt eine Eingabebearbeitung zwischen 0 und 1 durch. Sie ist positiver Natur. Es ist immer begrenzt, was bedeutet, dass seine Ausgabe nicht kleiner als 0 und mehr als 1 sein kann. Es nimmt auch streng an Natur zu, was bedeutet, dass mehr die höhere Ausgabe die Ausgabe wäre. Es kann definiert werden als

$$ F (x) \: = \: sigm (x) \: = \: \ frac {1} {1 \: + \: exp (-x)} $$
Bipolar sigmoidal function- Diese Aktivierungsfunktion führt eine Eingabebearbeitung zwischen -1 und 1 durch. Sie kann positiver oder negativer Natur sein. Es ist immer begrenzt, was bedeutet, dass seine Ausgabe nicht kleiner als -1 und mehr als 1 sein kann. Es nimmt auch in der Natur streng zu, wie die Sigmoidfunktion. Es kann definiert werden als

$$ F (x) \: = \: sigm (x) \: = \: \ frac {2} {1 \: + \: exp (-x)} \: - \: 1 \: = \: \ frac {1 \: - \: exp (x)} {1 \: + \: exp (x)} $$