Unbeaufsichtigtes Lernen

Wie der Name schon sagt, wird diese Art des Lernens ohne Aufsicht eines Lehrers durchgeführt. Dieser Lernprozess ist unabhängig. Während des Trainings von ANN unter unbeaufsichtigtem Lernen werden die Eingabevektoren ähnlichen Typs zu Clustern kombiniert. Wenn ein neues Eingabemuster angewendet wird, gibt das neuronale Netzwerk eine Ausgabeantwort aus, die die Klasse angibt, zu der das Eingabemuster gehört. Dabei würde es keine Rückmeldung von der Umgebung geben, was die gewünschte Ausgabe sein sollte und ob sie richtig oder falsch ist. Daher muss bei dieser Art des Lernens das Netzwerk selbst die Muster, Merkmale aus den Eingabedaten und die Beziehung für die Eingabedaten über die Ausgabe ermitteln.

Winner-Takes-All-Netzwerke

Diese Art von Netzwerken basiert auf der wettbewerbsorientierten Lernregel und verwendet die Strategie, bei der das Neuron mit den größten Gesamteingaben als Gewinner ausgewählt wird. Die Verbindungen zwischen den Ausgangsneuronen zeigen, dass die Konkurrenz zwischen ihnen und einem von ihnen "EIN" wäre, was bedeutet, dass es der Gewinner wäre und andere "AUS" wären.

Im Folgenden sind einige der Netzwerke aufgeführt, die auf diesem einfachen Konzept basieren und unbeaufsichtigtes Lernen verwenden.

Hamming-Netzwerk

In den meisten neuronalen Netzen, die unbeaufsichtigtes Lernen verwenden, ist es wichtig, die Entfernung zu berechnen und Vergleiche durchzuführen. Diese Art von Netzwerk ist ein Hamming-Netzwerk, bei dem für jeden gegebenen Eingangsvektor verschiedene Gruppen zusammengefasst werden. Im Folgenden sind einige wichtige Funktionen von Hamming Networks aufgeführt:

• Lippmann begann 1987 mit der Arbeit an Hamming-Netzwerken.

• Es ist ein Single-Layer-Netzwerk.

• Die Eingänge können entweder binär {0, 1} oder bipolar {-1, 1} sein.

• Die Gewichte des Netzes werden durch die beispielhaften Vektoren berechnet.

• Es ist ein Netzwerk mit festem Gewicht, was bedeutet, dass die Gewichte auch während des Trainings gleich bleiben.

Max Net

Dies ist auch ein Netzwerk mit fester Gewichtung, das als Subnetz für die Auswahl des Knotens mit der höchsten Eingabe dient. Alle Knoten sind vollständig miteinander verbunden, und in all diesen gewichteten Verbindungen sind symmetrische Gewichte vorhanden.

Die Architektur

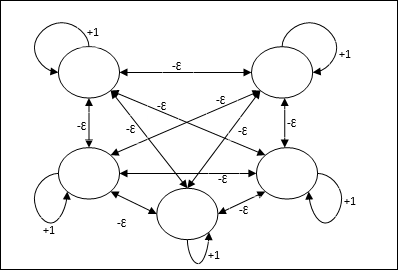
Es verwendet den Mechanismus, der ein iterativer Prozess ist, und jeder Knoten empfängt über Verbindungen hemmende Eingaben von allen anderen Knoten. Der einzelne Knoten, dessen Wert maximal ist, wäre aktiv oder Gewinner, und die Aktivierungen aller anderen Knoten wären inaktiv. Max Net verwendet die Identitätsaktivierungsfunktion mit $$ f (x) \: = \: \ begin {Fällen} x & if \: x> 0 \\ 0 & if \: x \ leq 0 \ end {Fälle} $$

Die Aufgabe dieses Netzes wird durch das Selbstanregungsgewicht von +1 und die Größe der gegenseitigen Hemmung erfüllt, die wie [0 <ɛ <$ \ frac {1} {m} $] eingestellt ist, wobei “m” ist die Gesamtzahl der Knoten.

Wettbewerbsfähiges Lernen in ANN

Es handelt sich um unbeaufsichtigtes Training, bei dem die Ausgabeknoten versuchen, miteinander zu konkurrieren, um das Eingabemuster darzustellen. Um diese Lernregel zu verstehen, müssen wir das Wettbewerbsnetz verstehen, das wie folgt erklärt wird:

Grundkonzept des Wettbewerbsnetzwerks

Dieses Netzwerk ist wie ein Single-Layer-Feed-Forward-Netzwerk mit einer Rückkopplungsverbindung zwischen den Ausgängen. Die Verbindungen zwischen den Ausgängen sind hemmend, was durch gepunktete Linien dargestellt wird, was bedeutet, dass sich die Konkurrenten niemals selbst unterstützen.

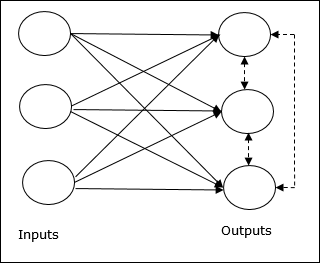
Grundkonzept der Wettbewerbsregel

Wie bereits erwähnt, würde es einen Wettbewerb zwischen den Ausgabeknoten geben, daher lautet das Hauptkonzept: Während des Trainings wird die Ausgabeeinheit, die für ein bestimmtes Eingabemuster die höchste Aktivierung aufweist, zum Gewinner erklärt. Diese Regel wird auch als Winner-Takes-All bezeichnet, da nur das Gewinner-Neuron aktualisiert wird und der Rest der Neuronen unverändert bleibt.

Mathematische Formulierung

Im Folgenden sind die drei wichtigen Faktoren für die mathematische Formulierung dieser Lernregel aufgeführt:

• Voraussetzung, um ein Gewinner zu sein

  Angenommen, ein Neuron y_k will der Gewinner sein, dann gäbe es folgende Bedingung

  $$ y_ {k} \: = \: \ begin {case} 1 & if \: v_ {k}> v_ {j} \: für \: all \: \: j, \: j \: \ neq \ : k \\ 0 & sonst \ end {Fälle} $$

  Es bedeutet, dass wenn irgendein Neuron, sagen wir, y_k will gewinnen, dann sein induziertes lokales Feld (die Ausgabe der Summationseinheit), sagen wir v_kmuss das größte unter allen anderen Neuronen im Netzwerk sein.

• Zustand der Gesamtsumme des Gewichts

  Eine weitere Einschränkung gegenüber der Regel des kompetitiven Lernens besteht darin, dass die Gesamtsumme der Gewichte für ein bestimmtes Ausgangsneuron 1 beträgt. Wenn wir beispielsweise ein Neuron betrachten k dann

  $$ \ displaystyle \ sum \ limit_ {k} w_ {kj} \: = \: 1 \: \: \: \: für \: all \: \: k $$

• Gewichtsänderung für den Gewinner

  Wenn ein Neuron nicht auf das Eingabemuster reagiert, findet in diesem Neuron kein Lernen statt. Wenn jedoch ein bestimmtes Neuron gewinnt, werden die entsprechenden Gewichte wie folgt angepasst:

  $$ \ Delta w_ {kj} \: = \: \ begin {case} - \ alpha (x_ {j} \: - \: w_ {kj}), & if \: neuron \: k \: gewinnt \\ 0 & if \: neuron \: k \: Verluste \ end {Fälle} $$

  Hier ist $ \ alpha $ die Lernrate.

  Dies zeigt deutlich, dass wir das gewinnende Neuron bevorzugen, indem wir sein Gewicht anpassen. Wenn ein Neuron verloren geht, müssen wir uns nicht die Mühe machen, sein Gewicht neu anzupassen.

K-bedeutet Clustering-Algorithmus

K-means ist einer der beliebtesten Clustering-Algorithmen, bei denen wir das Konzept der Partitionsprozedur verwenden. Wir beginnen mit einer anfänglichen Partition und verschieben Muster wiederholt von einem Cluster in einen anderen, bis wir ein zufriedenstellendes Ergebnis erhalten.

Algorithmus

Step 1 - Wählen Sie kPunkte als die anfänglichen Schwerpunkte. Initialisierenk Prototypen (w₁,…,w_k)Zum Beispiel können wir sie mit zufällig ausgewählten Eingabevektoren identifizieren -

$$ W_ {j} \: = \: i_ {p}, \: \: \: wobei \: j \: \ in \ lbrace1, ...., k \ rbrace \: und \: p \: \ in \ lbrace1, ...., n \ rbrace $$

Jeder Cluster C_j ist mit dem Prototyp verbunden w_j.

Step 2 - Wiederholen Sie die Schritte 3 bis 5, bis E nicht mehr abnimmt oder sich die Clustermitgliedschaft nicht mehr ändert.

Step 3 - Für jeden Eingabevektor i_p wo p ∈ {1,…,n}, stellen i_p im Cluster C_j* mit dem nächsten Prototyp w_j* mit der folgenden Beziehung

$$ | i_ {p} \: - \: w_ {j *} | \: \ leq \: | i_ {p} \: - \: w_ {j} |, \: j \: \ in \ lbrace1, ...., k \ rbrace $$

Step 4 - Für jeden Cluster C_j, wo j ∈ { 1,…,k}, aktualisieren Sie den Prototyp w_j der Schwerpunkt aller derzeit in C_j , damit

$$ w_ {j} \: = \: \ sum_ {i_ {p} \ in C_ {j}} \ frac {i_ {p}} {| C_ {j} |} $$

Step 5 - Berechnen Sie den Gesamtquantisierungsfehler wie folgt: -

$$ E \: = \: \ sum_ {j = 1} ^ k \ sum_ {i_ {p} \ in w_ {j}} | i_ {p} \: - \: w_ {j} | ^ 2 $$

Neocognitron

Es ist ein mehrschichtiges Feedforward-Netzwerk, das in den 1980er Jahren von Fukushima entwickelt wurde. Dieses Modell basiert auf überwachtem Lernen und wird zur visuellen Mustererkennung verwendet, hauptsächlich handgeschriebene Zeichen. Es handelt sich im Grunde genommen um eine Erweiterung des Cognitron-Netzwerks, das 1975 ebenfalls von Fukushima entwickelt wurde.

Die Architektur

Es ist ein hierarchisches Netzwerk, das viele Schichten umfasst, und in diesen Schichten gibt es lokal ein Konnektivitätsmuster.

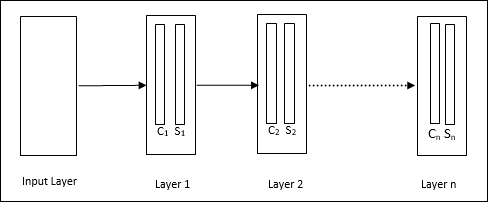
Wie wir im obigen Diagramm gesehen haben, ist Neocognitron in verschiedene verbundene Schichten unterteilt und jede Schicht hat zwei Zellen. Die Erklärung dieser Zellen ist wie folgt:

S-Cell - Es wird eine einfache Zelle genannt, die darauf trainiert ist, auf ein bestimmtes Muster oder eine Gruppe von Mustern zu reagieren.

C-Cell- Es handelt sich um eine komplexe Zelle, die die Ausgabe der S-Zelle kombiniert und gleichzeitig die Anzahl der Einheiten in jedem Array verringert. In einem anderen Sinne verdrängt die C-Zelle das Ergebnis der S-Zelle.

Trainingsalgorithmus

Es wurde festgestellt, dass das Training von Neocognitron Schicht für Schicht voranschreitet. Die Gewichte von der Eingabeebene zur ersten Ebene werden trainiert und eingefroren. Dann werden die Gewichte von der ersten Schicht zur zweiten Schicht trainiert und so weiter. Die internen Berechnungen zwischen S-Zelle und C-Zelle hängen von den Gewichten ab, die von den vorherigen Schichten stammen. Daher können wir sagen, dass der Trainingsalgorithmus von den Berechnungen für S-Zellen und C-Zellen abhängt.

Berechnungen in S-Zellen

Die S-Zelle besitzt das von der vorherigen Schicht empfangene Anregungssignal und die in derselben Schicht erhaltenen Hemmsignale.

$$ \ theta = \: \ sqrt {\ sum \ sum t_ {i} c_ {i} ^ 2} $$

Hier, t_i ist das feste Gewicht und c_i ist die Ausgabe von C-Zelle.

Die skalierte Eingabe der S-Zelle kann wie folgt berechnet werden:

$$ x \: = \: \ frac {1 \: + \: e} {1 \: + \: vw_ {0}} \: - \: 1 $$

Hier ist $ e \: = \: \ sum_i c_ {i} w_ {i} $

w_i ist das von C-Zelle zu S-Zelle eingestellte Gewicht.

w₀ ist das Gewicht, das zwischen dem Eingang und der S-Zelle einstellbar ist.

v ist die anregende Eingabe von der C-Zelle.

Die Aktivierung des Ausgangssignals ist,

$$ s \: = \: \ begin {Fälle} x, & if \: x \ geq 0 \\ 0, & if \: x <0 \ end {Fälle} $$

Berechnungen in C-Zellen

Der Nettoeingang der C-Schicht ist

$$ C \: = \: \ displaystyle \ sum \ limit_i s_ {i} x_ {i} $$

Hier, s_i ist die Ausgabe von S-Zelle und x_i ist das feste Gewicht von S-Zelle zu C-Zelle.

Die endgültige Ausgabe lautet wie folgt:

$$ C_ {out} \: = \: \ begin {case} \ frac {C} {a + C}, & if \: C> 0 \\ 0, andernfalls \ end {case} $$

Hier ‘a’ ist der Parameter, der von der Leistung des Netzwerks abhängt.