Vektorquantisierung lernen
Learning Vector Quantization (LVQ) unterscheidet sich von Vector Quantization (VQ) und Kohonen Self-Organizing Maps (KSOM) und ist im Grunde ein wettbewerbsfähiges Netzwerk, das überwachtes Lernen verwendet. Wir können es als einen Prozess zum Klassifizieren der Muster definieren, bei denen jede Ausgabeeinheit eine Klasse darstellt. Da das überwachte Lernen verwendet wird, erhält das Netzwerk eine Reihe von Trainingsmustern mit bekannter Klassifizierung sowie eine anfängliche Verteilung der Ausgabeklasse. Nach Abschluss des Trainingsprozesses klassifiziert LVQ einen Eingabevektor, indem es derselben Klasse wie die Ausgabeeinheit zugeordnet wird.
Die Architektur
Die folgende Abbildung zeigt die Architektur von LVQ, die der Architektur von KSOM sehr ähnlich ist. Wie wir sehen können, gibt es“n” Anzahl der Eingabeeinheiten und “m”Anzahl der Ausgabeeinheiten. Die Schichten sind vollständig mit Gewichten verbunden.

Verwendete Parameter
Im Folgenden sind die Parameter aufgeführt, die im LVQ-Trainingsprozess sowie im Flussdiagramm verwendet werden
x= Trainingsvektor (x 1 , ..., x i , ..., x n )
T = Klasse für Trainingsvektor x
wj = Gewichtsvektor für jth Ausgabeeinheit
Cj = Klasse, die dem zugeordnet ist jth Ausgabeeinheit
Trainingsalgorithmus
Step 1 - Referenzvektoren initialisieren, was wie folgt erfolgen kann -
Step 1(a) - Nehmen Sie aus dem angegebenen Satz von Trainingsvektoren den ersten “m”(Anzahl der Cluster) trainieren Vektoren und verwenden sie als Gewichtsvektoren. Die verbleibenden Vektoren können zum Training verwendet werden.
Step 1(b) - Weisen Sie das Anfangsgewicht und die Klassifizierung zufällig zu.
Step 1(c) - Wenden Sie die K-Mittel-Clustering-Methode an.
Step 2 - Referenzvektor $ \ alpha $ initialisieren
Step 3 - Fahren Sie mit den Schritten 4 bis 9 fort, wenn die Bedingung zum Stoppen dieses Algorithmus nicht erfüllt ist.
Step 4 - Befolgen Sie die Schritte 5 bis 6 für jeden Trainingseingabevektor x.
Step 5 - Berechnen Sie das Quadrat der euklidischen Entfernung für j = 1 to m und i = 1 to n
$$ D (j) \: = \: \ Anzeigestil \ Summe \ Grenzen_ {i = 1} ^ n \ Anzeigestil \ Summe \ Grenzen_ {j = 1} ^ m (x_ {i} \: - \: w_ {ij }) ^ 2 $$
Step 6 - Erhalten Sie die Gewinnereinheit J wo D(j) ist minimal.
Step 7 - Berechnen Sie das neue Gewicht der Gewinnereinheit anhand der folgenden Beziehung:
wenn T = Cj dann $ w_ {j} (neu) \: = \: w_ {j} (alt) \: + \: \ alpha [x \: - \: w_ {j} (alt)] $
wenn T ≠ Cj dann $ w_ {j} (neu) \: = \: w_ {j} (alt) \: - \: \ alpha [x \: - \: w_ {j} (alt)] $
Step 8 - Reduzieren Sie die Lernrate $ \ alpha $.
Step 9- Auf Stoppzustand prüfen. Es kann wie folgt sein:
- Maximale Anzahl von Epochen erreicht.
- Lernrate auf einen vernachlässigbaren Wert reduziert.
Flussdiagramm
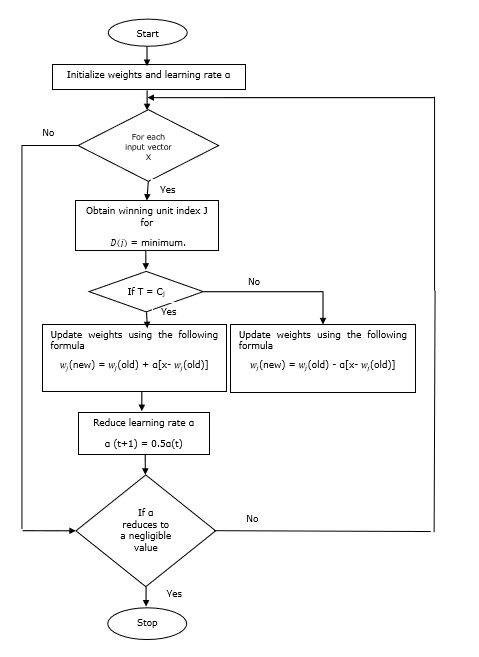
Varianten
Drei weitere Varianten, nämlich LVQ2, LVQ2.1 und LVQ3, wurden von Kohonen entwickelt. Die Komplexität in all diesen drei Varianten ist aufgrund des Konzepts, das sowohl der Gewinner als auch der Zweitplatzierte lernen werden, größer als in LVQ.
LVQ2
Wie diskutiert, wird das Konzept anderer Varianten von LVQ oben, der Zustand von LVQ2 durch Fenster gebildet. Dieses Fenster basiert auf den folgenden Parametern:
x - der aktuelle Eingabevektor
yc - der Referenzvektor, der am nächsten liegt x
yr - der andere Referenzvektor, der am nächsten ist x
dc - die Entfernung von x zu yc
dr - die Entfernung von x zu yr
Der Eingabevektor x fällt ins Fenster, wenn
$$ \ frac {d_ {c}} {d_ {r}} \:> \: 1 \: - \: \ theta \: \: und \: \: \ frac {d_ {r}} {d_ {c }} \:> \: 1 \: + \: \ theta $$
Hier ist $ \ theta $ die Anzahl der Trainingsmuster.
Die Aktualisierung kann mit der folgenden Formel erfolgen:
$ y_ {c} (t \: + \: 1) \: = \: y_ {c} (t) \: + \: \ alpha (t) [x (t) \: - \: y_ {c} (t)] $ (belongs to different class)
$ y_ {r} (t \: + \: 1) \: = \: y_ {r} (t) \: + \: \ alpha (t) [x (t) \: - \: y_ {r} (t)] $ (belongs to same class)
Hier ist $ \ alpha $ die Lernrate.
LVQ2.1
In LVQ2.1 nehmen wir nämlich die beiden nächsten Vektoren yc1 und yc2 und die Bedingung für Fenster ist wie folgt -
$$ Min \ begin {bmatrix} \ frac {d_ {c1}} {d_ {c2}}, \ frac {d_ {c2}} {d_ {c1}} \ end {bmatrix} \:> \ :( 1 \ : - \: \ theta) $$
$$ Max \ begin {bmatrix} \ frac {d_ {c1}} {d_ {c2}}, \ frac {d_ {c2}} {d_ {c1}} \ end {bmatrix} \: <\ :( 1 \ : + \: \ theta) $$
Die Aktualisierung kann mit der folgenden Formel erfolgen:
$ y_ {c1} (t \: + \: 1) \: = \: y_ {c1} (t) \: + \: \ alpha (t) [x (t) \: - \: y_ {c1} (t)] $ (belongs to different class)
$ y_ {c2} (t \: + \: 1) \: = \: y_ {c2} (t) \: + \: \ alpha (t) [x (t) \: - \: y_ {c2} (t)] $ (belongs to same class)
Hier ist $ \ alpha $ die Lernrate.
LVQ3
In LVQ3 nehmen wir nämlich die beiden nächsten Vektoren yc1 und yc2 und die Bedingung für Fenster ist wie folgt -
$$ Min \ begin {bmatrix} \ frac {d_ {c1}} {d_ {c2}}, \ frac {d_ {c2}} {d_ {c1}} \ end {bmatrix} \:> \ :( 1 \ : - \: \ theta) (1 \: + \: \ theta) $$
Hier $ \ theta \ ca. 0,2 $
Die Aktualisierung kann mit der folgenden Formel erfolgen:
$ y_ {c1} (t \: + \: 1) \: = \: y_ {c1} (t) \: + \: \ beta (t) [x (t) \: - \: y_ {c1} (t)] $ (belongs to different class)
$ y_ {c2} (t \: + \: 1) \: = \: y_ {c2} (t) \: + \: \ beta (t) [x (t) \: - \: y_ {c2} (t)] $ (belongs to same class)
Hier ist $ \ beta $ das Vielfache der Lernrate $ \ alpha $ und $\beta\:=\:m \alpha(t)$ für jeden 0.1 < m < 0.5