Andere Optimierungstechniken

Iterierte Gradientenabstiegstechnik

Der Gradientenabstieg, auch als steilster Abstieg bekannt, ist ein iterativer Optimierungsalgorithmus, um ein lokales Minimum einer Funktion zu finden. Während wir die Funktion minimieren, sind wir besorgt über die Kosten oder Fehler, die minimiert werden müssen (Remember Travelling Salesman Problem). Es wird häufig beim Deep Learning verwendet, was in einer Vielzahl von Situationen nützlich ist. Der Punkt, an den man sich erinnern sollte, ist, dass es um lokale Optimierung und nicht um globale Optimierung geht.

Hauptarbeitsidee

Mit Hilfe der folgenden Schritte können wir die Hauptarbeitsidee des Gradientenabstiegs verstehen:

Beginnen Sie zunächst mit einer ersten Vermutung der Lösung.
Nehmen Sie dann den Gradienten der Funktion an diesem Punkt.
Wiederholen Sie den Vorgang später, indem Sie die Lösung in die negative Richtung des Gradienten bewegen.

Wenn Sie die obigen Schritte ausführen, konvergiert der Algorithmus schließlich dort, wo der Gradient Null ist.

Mathematisches Konzept

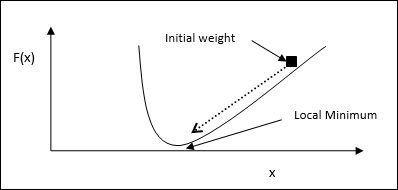
Angenommen, wir haben eine Funktion f(x)und wir versuchen, das Minimum dieser Funktion zu finden. Im Folgenden finden Sie die Schritte, um das Minimum von zu findenf(x).

Geben Sie zunächst einen Anfangswert $ x_ {0} \: für \: x $ an
Nehmen Sie nun den Gradienten $ \ nabla f $ ⁡ der Funktion mit der Intuition, dass der Gradient dabei die Steigung der Kurve ergibt x und seine Richtung zeigt auf die Zunahme der Funktion, um die beste Richtung herauszufinden, um sie zu minimieren.
Ändern Sie nun x wie folgt -

$$ x_ {n \: + \: 1} \: = \: x_ {n} \: - \: \ theta \ nabla f (x_ {n}) $$

Hier, θ > 0 ist die Trainingsrate (Schrittgröße), die den Algorithmus zu kleinen Sprüngen zwingt.

Schätzung der Schrittgröße

Eigentlich eine falsche Schrittweite θerreicht möglicherweise keine Konvergenz, daher ist eine sorgfältige Auswahl derselben sehr wichtig. Folgende Punkte müssen bei der Auswahl der Schrittweite beachtet werden

Wählen Sie keine zu große Schrittgröße, da dies sonst negative Auswirkungen hat, dh eher divergiert als konvergiert.
Wählen Sie keine zu kleine Schrittgröße, da die Konvergenz sonst viel Zeit in Anspruch nimmt.

Einige Optionen zur Auswahl der Schrittgröße -

Eine Möglichkeit besteht darin, eine feste Schrittgröße zu wählen.
Eine andere Möglichkeit besteht darin, für jede Iteration eine andere Schrittgröße zu wählen.

Simuliertes Tempern

Das Grundkonzept des Simulierten Glühens (SA) ist durch das Glühen in Festkörpern motiviert. Wenn wir beim Tempern ein Metall über seinen Schmelzpunkt erhitzen und abkühlen, hängen die strukturellen Eigenschaften von der Abkühlgeschwindigkeit ab. Wir können auch sagen, dass SA den metallurgischen Prozess des Glühens simuliert.

Verwendung in ANN

SA ist eine stochastische Berechnungsmethode, die von der Annealing-Analogie inspiriert ist, um die globale Optimierung einer bestimmten Funktion zu approximieren. Wir können SA verwenden, um vorwärtsgerichtete neuronale Netze zu trainieren.

Algorithmus

Step 1 - Generieren Sie eine zufällige Lösung.

Step 2 - Berechnen Sie die Kosten mit einer Kostenfunktion.

Step 3 - Generieren Sie eine zufällige benachbarte Lösung.

Step 4 - Berechnen Sie die neuen Lösungskosten mit derselben Kostenfunktion.

Step 5 - Vergleichen Sie die Kosten einer neuen Lösung mit denen einer alten Lösung wie folgt: -

Wenn Cost_{New Solution} < Cost_{Old Solution} Wechseln Sie dann zur neuen Lösung.

Step 6 - Testen Sie den Stoppzustand, bei dem es sich möglicherweise um die maximal erreichte Anzahl von Iterationen handelt, oder erhalten Sie eine akzeptable Lösung.