Optimierung mit Hopfield Network
Optimierung ist eine Aktion, um etwas wie Design, Situation, Ressource und System so effektiv wie möglich zu gestalten. Mit einer Ähnlichkeit zwischen der Kostenfunktion und der Energiefunktion können wir stark miteinander verbundene Neuronen verwenden, um Optimierungsprobleme zu lösen. Eine solche Art von neuronalem Netzwerk ist das Hopfield-Netzwerk, das aus einer einzelnen Schicht besteht, die ein oder mehrere vollständig verbundene wiederkehrende Neuronen enthält. Dies kann zur Optimierung verwendet werden.
Wichtige Punkte bei der Verwendung des Hopfield-Netzwerks zur Optimierung -
Die Energiefunktion muss ein Minimum des Netzwerks sein.
Es wird eine zufriedenstellende Lösung finden, anstatt eines aus den gespeicherten Mustern auszuwählen.
Die Qualität der vom Hopfield-Netzwerk gefundenen Lösung hängt wesentlich vom Ausgangszustand des Netzwerks ab.
Problem mit dem reisenden Verkäufer
Das Finden der kürzesten vom Verkäufer zurückgelegten Route ist eines der Rechenprobleme, die mithilfe des neuronalen Hopfield-Netzwerks optimiert werden können.
Grundkonzept von TSP
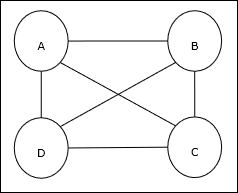
Travelling Salesman Problem (TSP) ist ein klassisches Optimierungsproblem, bei dem ein Verkäufer reisen muss nStädte, die miteinander verbunden sind, halten sowohl die Kosten als auch die zurückgelegte Strecke minimal. Zum Beispiel muss der Verkäufer eine Reihe von 4 Städten A, B, C, D bereisen. Ziel ist es, die kürzeste Rundreise ABC - D zu finden, um die Kosten zu minimieren, zu denen auch die Reisekosten gehören die letzte Stadt D zur ersten Stadt A.
Matrixdarstellung
Tatsächlich kann jede Tour durch n-city TSP ausgedrückt werden als n × n Matrix, deren ith Zeile beschreibt die ithLage der Stadt. Diese Matrix,Mkönnen für 4 Städte A, B, C, D wie folgt ausgedrückt werden:
$$ M = \ begin {bmatrix} A: & 1 & 0 & 0 & 0 \\ B: & 0 & 1 & 0 & 0 \\ C: & 0 & 0 & 1 & 0 \\ D: & 0 & 0 & 0 & 1 \ end {bmatrix} $$
Lösung von Hopfield Network
Bei der Betrachtung der Lösung dieses TSP durch das Hopfield-Netzwerk entspricht jeder Knoten im Netzwerk einem Element in der Matrix.
Berechnung der Energiefunktion
Um die optimierte Lösung zu sein, muss die Energiefunktion minimal sein. Auf der Grundlage der folgenden Einschränkungen können wir die Energiefunktion wie folgt berechnen:
Einschränkung-I
Die erste Einschränkung, auf deren Grundlage wir die Energiefunktion berechnen, besteht darin, dass ein Element in jeder Matrixzeile gleich 1 sein muss M und andere Elemente in jeder Zeile müssen gleich sein 0weil jede Stadt in der TSP-Tour nur an einer Position auftreten kann. Diese Einschränkung kann mathematisch wie folgt geschrieben werden:
$$ \ displaystyle \ sum \ limit_ {j = 1} ^ n M_ {x, j} \: = \: 1 \: für \: x \: \ in \: \ lbrace1, ..., n \ rbrace $ $
Nun enthält die zu minimierende Energiefunktion basierend auf der obigen Einschränkung einen Term proportional zu -
$$ \ displaystyle \ sum \ limit_ {x = 1} ^ n \ left (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ limit_ {j = 1} ^ n M_ {x, j } \ end {array} \ right) ^ 2 $$
Einschränkung-II
Wie wir wissen, kann in TSP eine Stadt an jeder Position der Tour auftreten, also in jeder Matrixspalte Mmuss ein Element gleich 1 sein und andere Elemente müssen gleich 0 sein. Diese Einschränkung kann mathematisch wie folgt geschrieben werden:
$$ \ displaystyle \ sum \ limit_ {x = 1} ^ n M_ {x, j} \: = \: 1 \: für \: j \: \ in \: \ lbrace1, ..., n \ rbrace $ $
Nun enthält die zu minimierende Energiefunktion basierend auf der obigen Einschränkung einen Term proportional zu -
$$ \ displaystyle \ sum \ limit_ {j = 1} ^ n \ left (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ limit_ {x = 1} ^ n M_ {x, j } \ end {array} \ right) ^ 2 $$
Kostenfunktionsberechnung
Nehmen wir eine quadratische Matrix von (n × n) bezeichnet durch C bezeichnet die Kostenmatrix von TSP für n Städte, in denen n > 0. Im Folgenden sind einige Parameter bei der Berechnung der Kostenfunktion aufgeführt:
Cx, y - Das Element der Kostenmatrix bezeichnet die Reisekosten von der Stadt x zu y.
Die Adjazenz der Elemente von A und B kann durch die folgende Beziehung gezeigt werden:
$$ M_ {x, i} \: = \: 1 \: \: und \: \: M_ {y, i \ pm 1} \: = \: 1 $$
Wie wir wissen, kann in Matrix der Ausgabewert jedes Knotens entweder 0 oder 1 sein, daher können wir für jedes Städtepaar A, B der Energiefunktion die folgenden Begriffe hinzufügen:
$$ \ displaystyle \ sum \ limit_ {i = 1} ^ n C_ {x, y} M_ {x, i} (M_ {y, i + 1} \: + \: M_ {y, i-1}) $$
Auf der Basis der obigen Kostenfunktion und des Beschränkungswerts wird die endgültige Energiefunktion E kann wie folgt angegeben werden -
$$ E \: = \: \ frac {1} {2} \ Anzeigestil \ Summe \ Grenzen_ {i = 1} ^ n \ Anzeigestil \ Summe \ Grenzen_ {x} \ Anzeigestil \ Summe \ Grenzen_ {y \ neq x} C_ {x, y} M_ {x, i} (M_ {y, i + 1} \: + \: M_ {y, i-1}) \: + $$
$$ \: \ begin {bmatrix} \ gamma_ {1} \ displaystyle \ sum \ limit_ {x} \ left (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ limit_ {i} M_ {x, i} \ end {array} \ right) ^ 2 \: + \: \ gamma_ {2} \ displaystyle \ sum \ limit_ {i} \ left (\ begin {array} {c} 1 \: - \ : \ displaystyle \ sum \ limit_ {x} M_ {x, i} \ end {array} \ right) ^ 2 \ end {bmatrix} $$
Hier, γ1 und γ2 sind zwei Wägekonstanten.