Selbstorganisierende Feature-Maps von Kohonen

Angenommen, wir haben ein Muster mit beliebigen Dimensionen, benötigen sie jedoch in einer oder zwei Dimensionen. Dann wäre der Prozess der Merkmalszuordnung sehr nützlich, um den breiten Musterraum in einen typischen Merkmalsraum umzuwandeln. Nun stellt sich die Frage, warum wir eine selbstorganisierende Feature-Map benötigen. Der Grund dafür ist, dass neben der Fähigkeit, die beliebigen Dimensionen in 1-D oder 2-D umzuwandeln, auch die Fähigkeit zur Beibehaltung der Nachbartopologie erhalten bleiben muss.

Nachbartopologien in Kohonen SOM

Es kann verschiedene Topologien geben, jedoch werden die folgenden zwei Topologien am häufigsten verwendet -

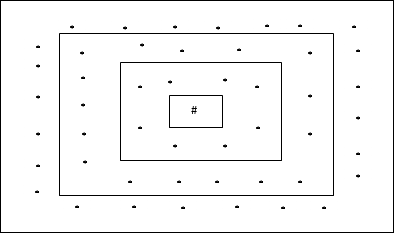
Rechteckige Gittertopologie

Diese Topologie hat 24 Knoten im Distanz-2-Gitter, 16 Knoten im Distanz-1-Gitter und 8 Knoten im Distanz-0-Gitter, was bedeutet, dass die Differenz zwischen jedem rechteckigen Gitter 8 Knoten beträgt. Die Gewinnereinheit wird durch # angezeigt.

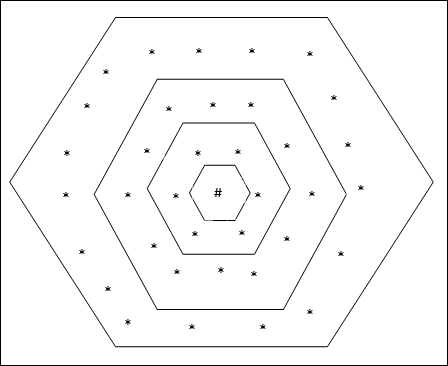
Hexagonale Gittertopologie

Diese Topologie hat 18 Knoten im Raster der Entfernung 2, 12 Knoten im Raster der Entfernung 1 und 6 Knoten im Raster der Entfernung 0, was bedeutet, dass die Differenz zwischen jedem rechteckigen Gitter 6 Knoten beträgt. Die Gewinnereinheit wird durch # angezeigt.

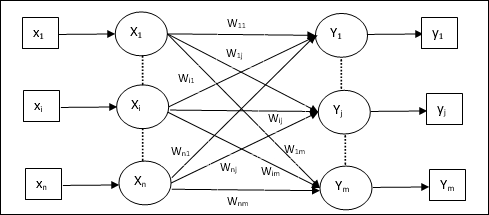
Die Architektur

Die Architektur von KSOM ähnelt der des Wettbewerbsnetzwerks. Mit Hilfe der zuvor diskutierten Nachbarschaftsprogramme kann das Training über die erweiterte Region des Netzwerks stattfinden.

Algorithmus für das Training

Step 1 - Initialisieren Sie die Gewichte, die Lernrate α und das nachbarschaftstopologische Schema.

Step 2 - Fahren Sie mit Schritt 3-9 fort, wenn die Stoppbedingung nicht erfüllt ist.

Step 3 - Fahren Sie für jeden Eingabevektor mit Schritt 4-6 fort x.

Step 4 - Berechnen Sie das Quadrat der euklidischen Entfernung für j = 1 to m

$$ D (j) \: = \: \ Anzeigestil \ Summe \ Grenzen_ {i = 1} ^ n \ Anzeigestil \ Summe \ Grenzen_ {j = 1} ^ m (x_ {i} \: - \: w_ {ij }) ^ 2 $$

Step 5 - Erhalten Sie die Gewinnereinheit J wo D(j) ist minimal.

Step 6 - Berechnen Sie das neue Gewicht der Gewinnereinheit anhand der folgenden Beziehung:

$$ w_ {ij} (neu) \: = \: w_ {ij} (alt) \: + \: \ alpha [x_ {i} \: - \: w_ {ij} (alt)] $$

Step 7 - Aktualisieren Sie die Lernrate α durch die folgende Beziehung -

$$ \ alpha (t \: + \: 1) \: = \: 0.5 \ alpha t $$

Step 8 - Reduzieren Sie den Radius des topologischen Schemas.

Step 9 - Überprüfen Sie, ob das Netzwerk gestoppt ist.