2D-Transformation

Transformation bedeutet, einige Grafiken durch Anwenden von Regeln in etwas anderes zu verwandeln. Wir können verschiedene Arten von Transformationen durchführen, z. B. Translation, Skalieren oder Verkleinern, Drehen, Scheren usw. Wenn eine Transformation in einer 2D-Ebene stattfindet, wird sie als 2D-Transformation bezeichnet.

Transformationen spielen in der Computergrafik eine wichtige Rolle, um die Grafiken auf dem Bildschirm neu zu positionieren und ihre Größe oder Ausrichtung zu ändern.

Homogene Koordinaten

Um eine Transformationssequenz wie Translation gefolgt von Rotation und Skalierung durchzuführen, müssen wir einem sequentiellen Prozess folgen -

• Übersetzen Sie die Koordinaten,
• Drehen Sie die übersetzten Koordinaten und dann
• Skalieren Sie die gedrehten Koordinaten, um die zusammengesetzte Transformation abzuschließen.

Um diesen Prozess zu verkürzen, müssen wir eine 3 × 3-Transformationsmatrix anstelle einer 2 × 2-Transformationsmatrix verwenden. Um eine 2 × 2-Matrix in eine 3 × 3-Matrix umzuwandeln, müssen wir eine zusätzliche Dummy-Koordinate W hinzufügen.

Auf diese Weise können wir den Punkt durch 3 Zahlen anstelle von 2 Zahlen darstellen, was aufgerufen wird Homogenous CoordinateSystem. In diesem System können wir alle Transformationsgleichungen in der Matrixmultiplikation darstellen. Jeder kartesische Punkt P (X, Y) kann durch P '(X _h , Y _h , h) in homogene Koordinaten umgewandelt werden .

Übersetzung

Eine Übersetzung verschiebt ein Objekt an eine andere Position auf dem Bildschirm. Sie können einen Punkt in 2D übersetzen, indem Sie der ursprünglichen Koordinate (X, Y) eine Übersetzungskoordinate (t _x , t _y ) hinzufügen , um die neue Koordinate (X ', Y') zu erhalten.

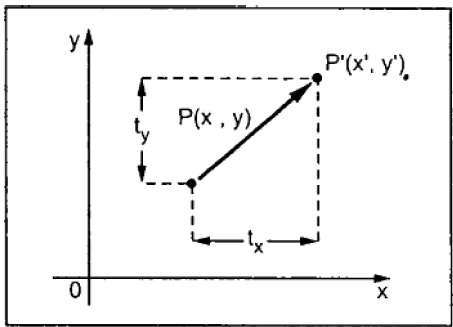
Aus der obigen Abbildung können Sie Folgendes schreiben:

X’ = X + t_x

Y’ = Y + t_y

Das Paar (t _x , t _y ) wird als Translationsvektor oder Verschiebungsvektor bezeichnet. Die obigen Gleichungen können auch unter Verwendung der Spaltenvektoren dargestellt werden.

$ P = \ frac {[X]} {[Y]} $ p '= $ \ frac {[X']} {[Y ']} $ T = $ \ frac {[t_ {x}]} {[ t_ {y}]} $

Wir können es schreiben als -

P’ = P + T

Drehung

Bei der Drehung drehen wir das Objekt um einen bestimmten Winkel θ (Theta) von seinem Ursprung. Aus der folgenden Abbildung ist ersichtlich, dass der Punkt P (X, Y) im Winkel φ von der horizontalen X-Koordinate mit dem Abstand r vom Ursprung liegt.

Nehmen wir an, Sie möchten es um den Winkel θ drehen. Nachdem Sie es an eine neue Position gedreht haben, erhalten Sie einen neuen Punkt P '(X', Y ').

Unter Verwendung der Standardtrigonometrie kann die ursprüngliche Koordinate des Punktes P (X, Y) als - dargestellt werden

$ X = r \, cos \, \ phi ...... (1) $

$ Y = r \, sin \, \ phi ...... (2) $

Genauso können wir den Punkt P '(X', Y ') darstellen als -

$ {x} '= r \: cos \: \ left (\ phi \: + \: \ theta \ right) = r \: cos \: \ phi \: cos \: \ theta \: - \: r \ : sin \: \ phi \: sin \: \ theta ....... (3) $

$ {y} '= r \: sin \: \ left (\ phi \: + \: \ theta \ right) = r \: cos \: \ phi \: sin \: \ theta \: + \: r \ : sin \: \ phi \: cos \: \ theta ....... (4) $

Wenn wir die Gleichungen (1) und (2) in (3) und (4) einsetzen, erhalten wir

$ {x} '= x \: cos \: \ theta - \: y \: sin \: \ theta $

$ {y} '= x \: sin \: \ theta + \: y \: cos \: \ theta $

Darstellung der obigen Gleichung in Matrixform,

$$ [X 'Y'] = [XY] \ begin {bmatrix} cos \ theta & sin \ theta \\ −sin \ theta & cos \ theta \ end {bmatrix} ODER $$

P '= P. R.

Wobei R die Rotationsmatrix ist

$$ R = \ begin {bmatrix} cos \ theta & sin \ theta \\ −sin \ theta & cos \ theta \ end {bmatrix} $$

Der Drehwinkel kann positiv und negativ sein.

Für einen positiven Drehwinkel können wir die obige Drehmatrix verwenden. Bei einer Drehung mit negativem Winkel ändert sich die Matrix jedoch wie unten gezeigt -

$$ R = \ begin {bmatrix} cos (- \ theta) & sin (- \ theta) \\ -sin (- \ theta) & cos (- \ theta) \ end {bmatrix} $$

$$ = \ begin {bmatrix} cos \ theta & −sin \ theta \\ sin \ theta & cos \ theta \ end {bmatrix} \ left (\ weil cos (- \ theta) = cos \ theta \; und \; sin (- \ theta) = −sin \ theta \ right) $$

Skalierung

Um die Größe eines Objekts zu ändern, wird die Skalierungstransformation verwendet. Während des Skalierungsprozesses erweitern oder komprimieren Sie die Abmessungen des Objekts. Die Skalierung kann erreicht werden, indem die ursprünglichen Koordinaten des Objekts mit dem Skalierungsfaktor multipliziert werden, um das gewünschte Ergebnis zu erhalten.

Nehmen wir an, dass die ursprünglichen Koordinaten (X, Y), die Skalierungsfaktoren (S _X , S _Y ) und die erzeugten Koordinaten (X ', Y') sind. Dies kann mathematisch wie unten dargestellt dargestellt werden -

X' = X . S_X and Y' = Y . S_Y

Der Skalierungsfaktor S _X , S _Y skaliert das Objekt in X- bzw. Y-Richtung. Die obigen Gleichungen können auch in Matrixform wie folgt dargestellt werden:

$$ \ binom {X '} {Y'} = \ binom {X} {Y} \ begin {bmatrix} S_ {x} & 0 \\ 0 & S_ {y} \ end {bmatrix} $$

ODER

P’ = P . S

Wobei S die Skalierungsmatrix ist. Der Skalierungsprozess ist in der folgenden Abbildung dargestellt.

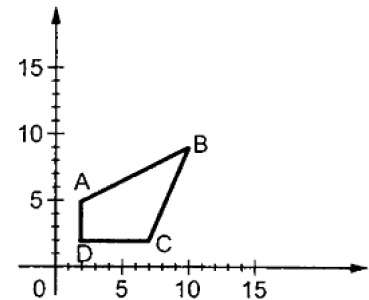
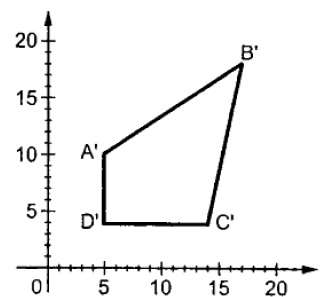
Wenn wir dem Skalierungsfaktor S Werte unter 1 geben, können wir die Größe des Objekts reduzieren. Wenn wir Werte größer als 1 angeben, können wir das Objekt vergrößern.

Betrachtung

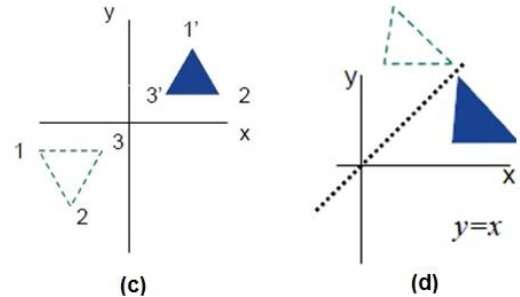
Reflexion ist das Spiegelbild des Originalobjekts. Mit anderen Worten können wir sagen, dass es sich um eine Rotationsoperation mit 180 ° handelt. Bei der Reflexionstransformation ändert sich die Größe des Objekts nicht.

Die folgenden Abbildungen zeigen Reflexionen in Bezug auf die X- und Y-Achse bzw. über den Ursprung.

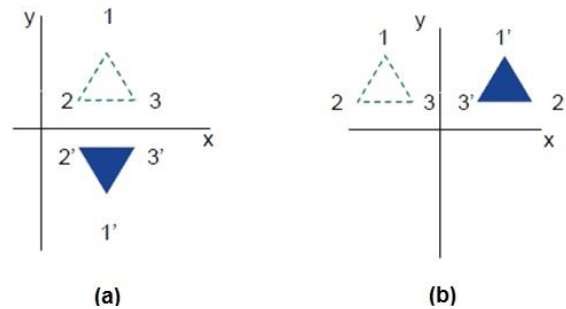
Scheren

Eine Transformation, die die Form eines Objekts neigt, wird als Schertransformation bezeichnet. Es gibt zwei ScherumwandlungenX-Shear und Y-Shear. Man verschiebt X-Koordinatenwerte und andere verschiebt Y-Koordinatenwerte. Jedoch; In beiden Fällen ändert nur eine Koordinate ihre Koordinaten und die andere behält ihre Werte bei. Scheren wird auch als bezeichnetSkewing.

X-Shear

Die X-Scherung behält die Y-Koordinate bei und es werden Änderungen an den X-Koordinaten vorgenommen, wodurch die vertikalen Linien nach rechts oder links geneigt werden (siehe Abbildung unten).

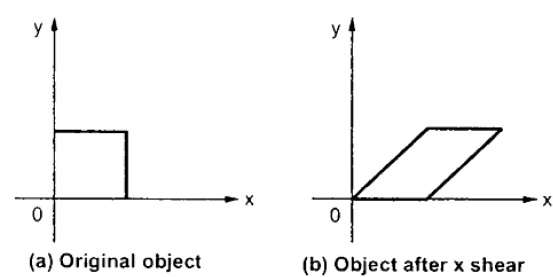
Die Transformationsmatrix für X-Shear kann wie folgt dargestellt werden:

$$ X_ {sh} = \ begin {bmatrix} 1 & shx & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} $$

Y '= Y + Sh _y . X.

X '= X.

Y-Shear

Die Y-Scherung behält die X-Koordinaten bei und ändert die Y-Koordinaten, wodurch sich die horizontalen Linien in Linien verwandeln, die wie in der folgenden Abbildung gezeigt nach oben oder unten geneigt sind.

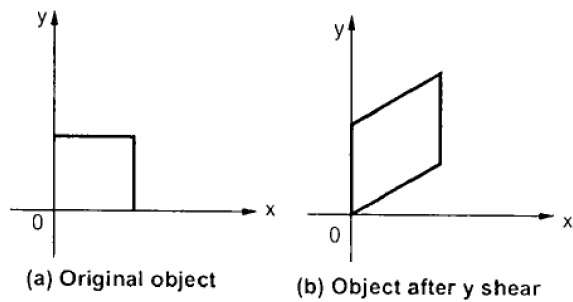
Die Y-Scherung kann in der Matrix dargestellt werden als -

$$ Y_ {sh} \ begin {bmatrix} 1 & 0 & 0 \\ schüchtern & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} $$

X '= X + Sh _x . Y.

Y '= Y.

Zusammengesetzte Transformation

Wenn auf eine Transformation der Ebene T1 eine Transformation der zweiten Ebene T2 folgt, kann das Ergebnis selbst durch eine einzelne Transformation T dargestellt werden, die die Zusammensetzung von T1 und T2 in dieser Reihenfolge darstellt. Dies wird geschrieben als T = T1 ∙ T2.

Eine zusammengesetzte Transformation kann durch Verketten von Transformationsmatrizen erreicht werden, um eine kombinierte Transformationsmatrix zu erhalten.

Eine kombinierte Matrix -

[T][X] = [X] [T1] [T2] [T3] [T4] …. [Tn]

Wobei [Ti] eine beliebige Kombination von ist

• Translation
• Scaling
• Shearing
• Rotation
• Reflection

Die Änderung der Transformationsreihenfolge würde zu unterschiedlichen Ergebnissen führen, da die Matrixmultiplikation im Allgemeinen nicht kumulativ ist, dh [A]. [B] ≠ [B]. [A] und die Reihenfolge der Multiplikation. Der Hauptzweck des Zusammenstellens von Transformationen besteht darin, Effizienz zu erzielen, indem eine einzelne zusammengesetzte Transformation auf einen Punkt angewendet wird, anstatt eine Reihe von Transformationen nacheinander anzuwenden.

Um beispielsweise ein Objekt um einen beliebigen Punkt (X _p , Y _p ) zu drehen , müssen drei Schritte ausgeführt werden:

• Verschieben Sie den Punkt (X _p , Y _p ) in den Ursprung.
• Drehen Sie es um den Ursprung.
• Verschieben Sie schließlich das Rotationszentrum dorthin zurück, wo es hingehört.